发电机滑模励磁控制器设计
2015-10-31乔鹤
乔鹤
(东北电力大学电气工程学院,吉林吉林 132012)
发电机滑模励磁控制器设计
乔鹤
(东北电力大学电气工程学院,吉林吉林132012)
本文结合了自适应逆推法与L2增益干扰抑制以及Terminal滑模控制,首先将控制器的推理与设计的整个过程加以给出,然后对2区域4机系统加以仿真,并深入分析了其仿真结果,结果表明Terminal滑模励磁控制器具备较好的性能,它不仅使得功率振荡能够得到快速抑制,并使得电力系统其暂态稳定性得以提高,而且使得机端电压得以恒定。
自适应逆推法Terminal滑模控制电力系统
本文结合了自适应逆推法与L2增益干扰抑制以及Terminal滑模控制,以便使得控制效果最佳,并将它求出。新的控制方法能够镇定非线性系统,尽管非线性系统包含了不确定参数并且受外扰动的影响。在发电机励磁控制器中应用此控制方法,并且将COI信号的跟踪加以实现。
1 数学模型
在发电机其机械功率不变的前提下,采用快速励磁,也就是说将励磁机本身的动态加以忽略,则可以得到电力系统的状态方程:

其中分别 iε为不确定项,包括建模不精确与外扰动部分; iT为阻尼系数,也是不确定的参数; δ为发电机的功角; w为发电机转子的角速度; d为惯性时间变量; p为机械功率,假定是不变动的;E为励磁电压,即设计后的控制量。
COI信号被定义为:


图1 两区域四机系统示意图

图2 三相短路时的响应曲线

图3 COI时滞对G1与G4功角差的影响
2 控制器设计
考虑到模型中含有不确定参数以及外扰动的三阶不确定性系统,即:
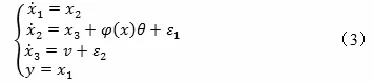
其中, 1x、 2x和 3x是输入和输出的控制量, θ为一个有界限的不确定扰动, φ是不确定参数,对应着已知函数。在整个控制系统之中,L2增益干扰抑制,它的控制目标为寻找到一个合适的输入量,使得在给定的正常数的条件下,能够有:

将Terminal滑模面加入其中令
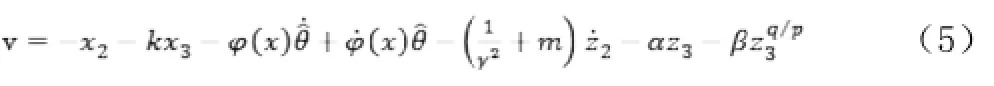
邻域对应的半径小于,只要选取的参数和足够大,就可以保证该领域足够的小。由此实现了L2增益干扰抑制控制。
3 数值仿真
在本文中主要采用两区域四机系统,如图1。发电机使用的模型为六阶模型,负荷采用恒定功率模型。由于仿真还受控制器自身限幅的影响,因此也考虑了这方面的因素。
试验测试时间为t=0.1s时,第7节点与第8节点间与第7节点近侧出现三相接地短路,时间t=0.2s时,在线路故障被排除后,进行仿真,其结果如图2。通过对图1中的发电机功角波形的分析可以得出,上述的控制策略能够让功角更迅速的稳定,超调量也会更加小些;在电压控制上,逆推励磁控制下的机端电压大多数时间会低于额定值,但上述的控制器能够让机端电压快速恢复到额定值。
COI信号要利用广域测量系统得到,通常来讲,信号时滞要达到几百毫秒。图3表示的是G1和G4的功角差受COI信号时滞的影响(第1、2、3曲线分别对应的时滞为200ms、300ms和500ms)。通过图3可以看出,当信号的时滞不大于300ms,系统稳定控制就不会受到时滞太大的影响,且本文的控制方法仍占有一定优势。当信号的时滞大于500ms,功角将趋于震荡或者发散。因此,可接受的时滞的取值范围大约为300~500ms。
4 结语
本文将L2增益干扰抑制、自适应逆推法和Terminal滑模控制相组合,提出了基于自适应鲁棒的Terminal滑模控制方法,并将其成功的应用到发电机的励磁控制器研发中。
[1]王晓东,张俊岭,王刚.电力系统励磁控制器设计[J].科技致富向导,2014(10).
[2]蔡超豪.非线性H∞励磁控制器的设计[J].东北电力大学学报,2010(03).
乔鹤(1988—),女,吉林人,硕士研究生,毕业于东北电力大学,研究方向:电气工程及自动化。
