不敏卡尔曼滤波方法研究

肖贤　张维中

（1.西安铁路职业技术学院，陕西西安　710014；2.西北工业大学，陕西西安　710072）

不敏卡尔曼滤波方法研究

肖贤1张维中2

（1.西安铁路职业技术学院，陕西西安710014；2.西北工业大学，陕西西安710072）

针对卡尔曼滤波（KF）在对非线性目标系统目标跟踪问题时易出现跟踪精度较低，滤波发散等问题，将不敏卡尔曼滤波器（UKF）运用在非线性系统的目标跟踪中。通过不敏卡尔曼滤波器在非线性目标跟踪中的应用和仿真结果比较表明，不敏卡尔曼滤波与传统卡尔曼滤波器和扩展卡尔曼滤波器（EKF）相比，提高了滤波精度，改善了滤波性能，具有较好的跟踪效果。

不敏卡尔曼滤波机动目标Matlab扩展卡尔曼滤波非线性系统

卡尔曼滤波器［1］依据最小均方误差准则获得目标的动态估计，但是在实际系统中，大部分的观测数据与目标的动态参数之间的关系均是非线性的。对于非线性的滤波问题，很多方法对此传统的卡尔曼滤波算法进行了扩展研究。其中比较突出的是EKF，UCMKF，PF等方法。通常对于非线性系统的处理的办法是运用线性化将非线性的问题转换成线性问题，套用KF来进行求解。当系统的动态模型与观测模型所得到的线性化误差较大时，滤波器跟踪容易发散，在对非线性系统进行kalman滤波时，必须求非线性函数的Jacobi矩阵，对于摩西复杂的系统，求取方法繁琐且容易出错。另外，在工程应用之中，模型线性化过程较为复杂，不易得到。如果假设模型与真是模型不相符合，就会出现滤波发散。引起滤波发散的主要原因包括，系统过程噪声与量测噪声参数选取对过程噪声影响较大、系统初始状态和初始协方差的假设值偏差过大、不准确线性化或者降维处理、计算误差。

1　卡尔曼滤波器与扩展卡尔曼滤波器［2］

1.1卡尔曼滤波器

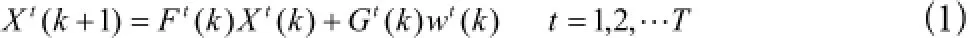
其中，）（kFt，）（kGt为已知矩阵，噪声向量）（kwt是具有零均值和已知协方差矩阵且与目标初始状态统计独立的高斯随机向量。

图1　目标运动轨迹

设）（km为k时刻确认矩阵的量测数，则目标的状态方程为：

其中，测量矩阵）（kHt是已知的，每个）（kVt都是与所有其他噪声向量独立的零均值高斯噪声向量，其协方差矩阵是已知的。

应用kalman滤波器步骤如下所示：

（1）状态一步预测：

（2）状态估计：

（3）滤波增益：

（4）一步预测均方误差：

（5）估计均方误差：

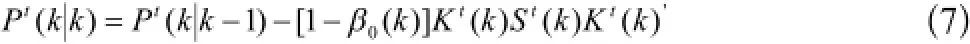
1.2扩展卡尔曼滤波器［3-5］

在实际应用系统中，其量测以及过程通常是非线性的，不能够直接运用卡尔曼滤波器。但是我们可以通过泰勒级数展开的方式，获得非线性系统的线性近似表达式，从而采用卡尔曼滤波算法，用来解决非线性问题。这就是扩展卡尔曼滤波器（Extended KalmanFilter，EKF）。

图2　误差轨迹

扩展卡尔曼滤波针对非线性量测方程h（X）在Xˆ（kk-1）处做泰勒展开并取得其一次项，可得：

利用导数线性化的卡尔曼滤波算法的精度依赖于目标状态动态模型以及以前的状态估计。如能够保证充分小，就能够达到一定的滤波精度。EKF虽然被广泛的运用于解决非线性系统的状态估计问题，但是其滤波效果在很多复杂系统之中难以令人满意，模型线性化误差最终会影响目标的估计精度，甚至导致发散。引入了一种新的滤波方法。

2　不敏卡尔曼滤波［6-9］

不敏卡尔曼滤波是运用不敏变化的思想对卡尔曼滤波器进行改进得到的一种新算法。此算法用有线的参数来近似随机量的统计特性，用一组精确的sigma点经过非线性模型的映射来传递随机信息的特性。假设非线性系统中的状态向量的初始均值与协方差为

UKF算法中的初始向量是由原始向量，过程噪声以及量测噪声组成［10］。其初始值和协方差定义如下：

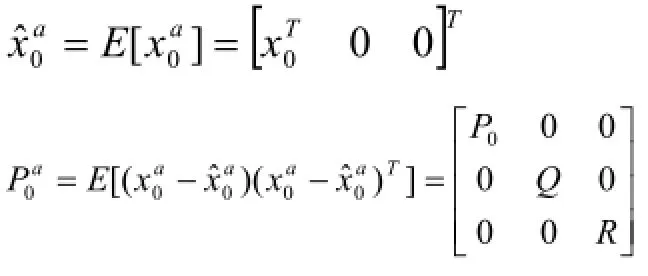
Q与R为过程噪声与量测噪声的协方差阵。不敏卡尔曼滤波器的过程如下所示：

（1）用不敏变换过程中的方法计算sigma点的权值，并运用下式计算sigma点

（2）sigma点的一步预测：

（3）状态预测：

（4）计算量测预测采样点：

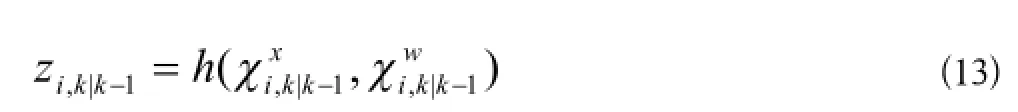
（5）估计量测预测值：

（6）估计信息协方差矩阵：

（7）估计互协方差矩阵：

（8）计算增益矩阵：

（9）状态更新：

（10）协方差更新：

3　仿真实验

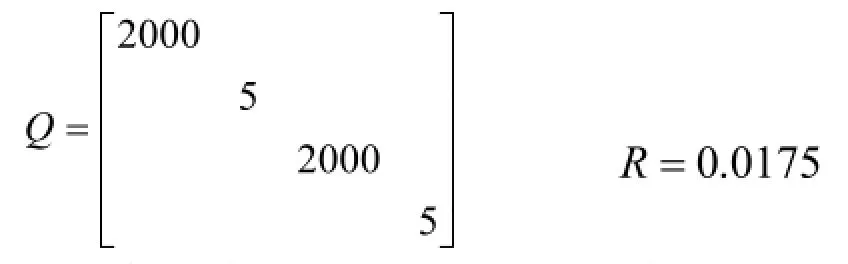
图1描述载机与目标在二维环境中的运动。雷达总采样100个时间周期，载机与目标机均做匀速直线运动，载机初始状态［1e5 16 1e5 0］，目标机初始运动状态为［2e5 10 2e5 -10］。

经过100次蒙特卡洛仿真，每次仿真时间为100s，采样间隔为1s。设定均方根误差作为测量指标。均方根误差的定义为：

从图2中可以看出利用KF方法的估计性能最差，利用EKF方法能够得到较好的估计，但是仍然与真实估计由较大差距，而UKF方法能够得到更高的估计精度。仿真实验结果证实了所提出方法的有效性。

4　结语

传统卡尔曼滤波技术在对非线性目标进行跟踪的过程中，因状态方程的单一性会大大降低目标跟踪精度，为了改善目标跟踪性能运用不敏卡尔曼滤波技术提高了滤波精度，改善了滤波性能，通过仿真表明UKF可以使得非线性系统滤波具有较高的精度，对噪声也具有较好的适应性能。

［1］Kalman R E. A new approach to linear filtering and prediction problems［J］. Journal of Fluids Engineering， 1960， 82（1）：35-45.

［2］永元，洪钺，自动化技术研究者，等.卡尔曼滤波与组合导航原理［M］.西北工业大学出版社，1998.

［3］Reif K， Unbehauen R. The extended Kalman filter as an exponential observer for nonlinear systems［J］.IEEE Transactions on Signal Processing，1999，47（8）： 2324-2328.

［4］范文兵，刘春风，张素贞.一种强跟踪扩展卡尔曼滤波器的改进算［5］Julier S J， Uhlmann J K. New extension of the Kalman filter to nonlinear systems［C］//AeroSense'97. International Society for Optics and Photonics，1997： 182-193.

法［J］.控制与决策，2006，21（1）：73-76.

［6］杨柏胜，姬红兵.基于无迹卡尔曼滤波的被动多传感器融合跟踪［J］.控制与决策，2008， 23（4）： 460-463.

［7］刘华，黄胜昔.基于序贯无迹卡尔曼滤波的雷达目标跟踪方法［J］. Computer Engineering and Applications，2009，45（25）.

［8］叶斌，徐毓.强跟踪滤波器与卡尔曼滤波器对目标跟踪的比较［J］.空军雷达学院学报，2002， 16（2）： 17-19.

［9］Xiong K，Zhang H Y， Chan C W. Performance evaluation of UKF-based nonlinear filtering［J］. Automatica， 2006， 42（2）： 261-270.

［10］Kolås S， Foss B A， Schei T S. Constrained nonlinear state estimation based on the UKF approach［J］. Computers & Chemical Engineering， 2009， 33（8）： 1386-1401.

肖贤（1988—），男，陕西省西安市人，西安铁路职业技术学院，助教，学士，研究方向：自动控制、信息融合。