机电控制CVT夹紧力可变机构性能分析

叶　明　李　鑫　罗　勇

重庆理工大学汽车零部件先进制造技术教育部重点实验室，重庆，400054

机电控制CVT夹紧力可变机构性能分析

叶明李鑫罗勇

重庆理工大学汽车零部件先进制造技术教育部重点实验室，重庆，400054

机电控制CVT采用直流电机作为调速驱动机构，比传统的电控液动CVT具有更高的效率、更好的控制性能和更少的零件数目。针对目前机电控制CVT夹紧力不可调的缺点，提出一种CVT夹紧力调整的机构，并建立了数学模型。在此基础上设计了基于模糊控制和比例积分控制的位置与速度双闭环控制算法，并进行了夹紧力调整控制仿真。结果表明，所提出的夹紧力调整机构和控制策略具有较好的控制性能，满足系统运行过程中夹紧力变化的需要。

机电控制CVT；可变夹紧力；控制；仿真

0　引言

金属带式无级自动变速传动(continuously variable transmission, CVT)与整车匹配具有良好的调速平顺性和燃油经济性，在车辆传动系统中得到了较为广泛的应用。传统的CVT采用电控液动的方式，通过电磁阀控制液压缸推动CVT带轮的轴向移动实现调速[1]。电控液动CVT自身需要一套液压系统，因此，制造成本和效率损失相对较高，并且在发动机零转速下不能建立压力传递转矩，进入工作状态的时间也相对较长[2]。基于以上特征，传统CVT在具有纯电动工况的电动车和经济型车辆上的应用受到一定限制[3]。机电控制CVT采用电机通过机械传动系统来推动CVT带轮，实现调速[4]。由于没有液压系统，CVT效率大大提高。根据测试，机电控制CVT效率达到了93.6%，较传统的电控液动式CVT提高了10%。由于采用电机驱动，控制精度和响应速度也可得到提高，同时系统的零件数目大大减少，因此，机电控制CVT有着广阔的应用前景。目前，机电控制CVT的夹紧力采用碟簧加压，一般按照满足传递最大转矩需求施加夹紧力[5]。这会使得系统的寿命和效率都受到影响。如果能够使夹紧力所需求转矩变化而调整，就可使系统不必始终受到最大夹紧力，从而提高系统寿命和效率[6]。本文针对机电控制CVT夹紧力不可调的缺点，提出一种CVT夹紧力调整的机构，并建立仿真模型，对该机构夹紧力调整的性能进行仿真。

1　机电控制CVT结构

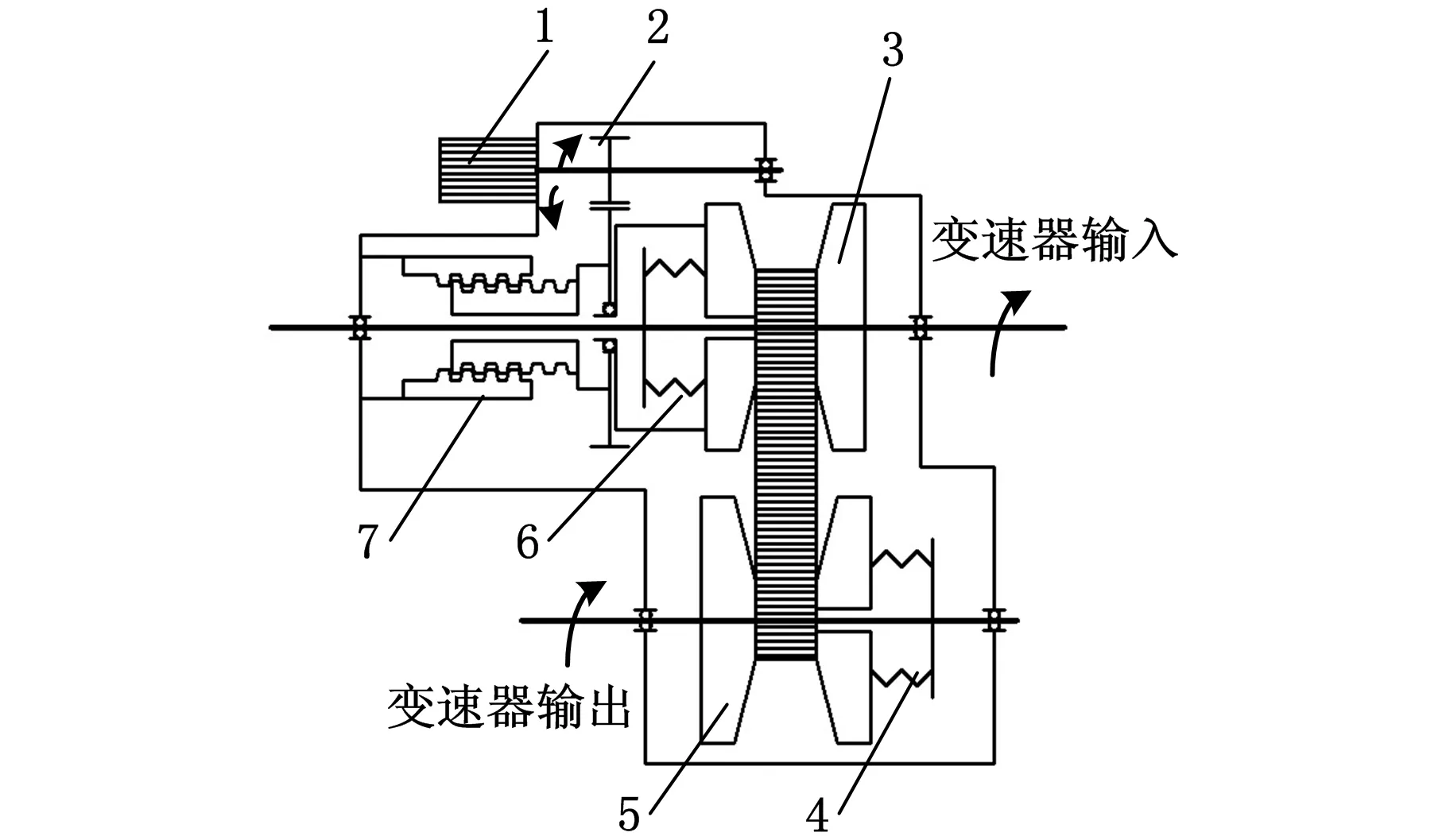
1.调速电机　2.齿轮减速机构　3.主动带轮　4.碟簧　5.从动带轮　6.碟簧　7.丝杆螺母机构图1　机电控制CVT结构原理

图1是机电控制CVT的结构原理图。从图中可以看出，动力经变速器输入端输入，通过主动带轮和金属带，由从动带轮输出，实现动力传递。机电控制CVT的调速机构由驱动机构、夹紧机构和金属带传动装置构成。驱动机构采用直流电机，通过齿轮减速机构和丝杆螺母机构，实现电机的减速增扭，并将电机的旋转运动转换为直线运动，驱动主动带轮动轮做轴向移动。夹紧机构采用碟簧，通过其弹性变形实现对带轮的加压。金属带传动装置和传统的电控液动金属带CVT相同，由钢带和金属块组成，通过带轮的加紧，传递动力。调速机构的动力传递路线为：调速电机-齿轮减速机构-丝杆螺母机构-主动带轮动轮。在上述结构中，CVT传递转矩能力取决于从动带轮夹紧碟簧(4)。而碟簧为机械弹性原件，在某一位置只能施加固定的压力。因此，碟簧的弹性特性必须保证在不同速比位置传递系统所需的最大转矩。而在大部分工况中，CVT不需要传递最大转矩，这就使得很大一部分夹紧力处于富余状态[7]。而过大的夹紧力会降低零部件寿命和效率[8]。因此，夹紧力应该随传递转矩的大小而改变，以提高系统寿命，减小关键零部件尺寸，并提高效率。

根据上述分析，本文提出一种机电控制CVT夹紧力调整机构，如图2所示。当系统需求转矩突然增大时，夹紧力调整电机旋转，带动夹紧力调整减速齿轮，实现减速增扭。丝杆螺母机构将旋转运动转换为直线运动，将夹紧力调整弹簧压缩，增大夹紧力，保证系统传递足够的转矩。当系统需求转矩降低时，夹紧力调整电机驱动丝杆螺母机构放松夹紧力调整弹簧，减小夹紧力。从而使系统夹紧力随转矩需求变化。整个过程中，助力弹簧可抵消部分夹紧力调整弹簧的压力，降低夹紧力调整电机的负荷，提高系统的响应速度。系统的最小夹紧力取决于从动轮夹紧碟簧。夹紧力调整机构的动力传递路线为：夹紧力调整电机-夹紧力调整减速齿轮-夹紧力调整丝杆螺母-夹紧力调整碟簧-从动带轮动轮。本研究主要计算参数见表1。

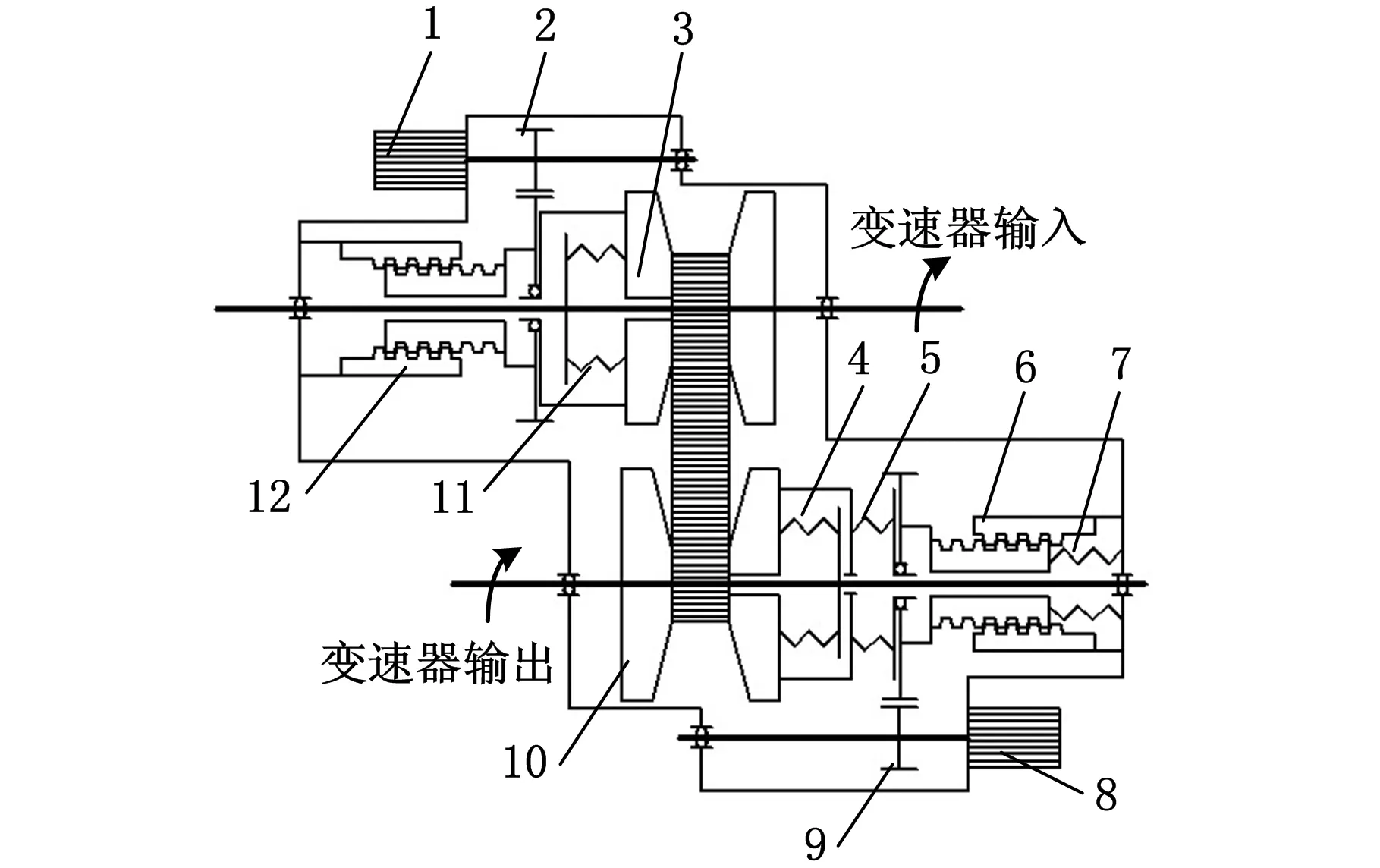
1.调速电机　2.齿轮减速机构　3.主动带轮　4.从动轮夹紧碟簧　5.夹紧力调整碟簧　6.夹紧力调整丝杠螺母机构　7.助力碟簧　8.夹紧力调整电机　9.夹紧力调整减速齿轮　10.从动带轮　11.主动轮碟簧　12.调速丝杆螺母机构图2　机电控制CVT夹紧力可调机构原理

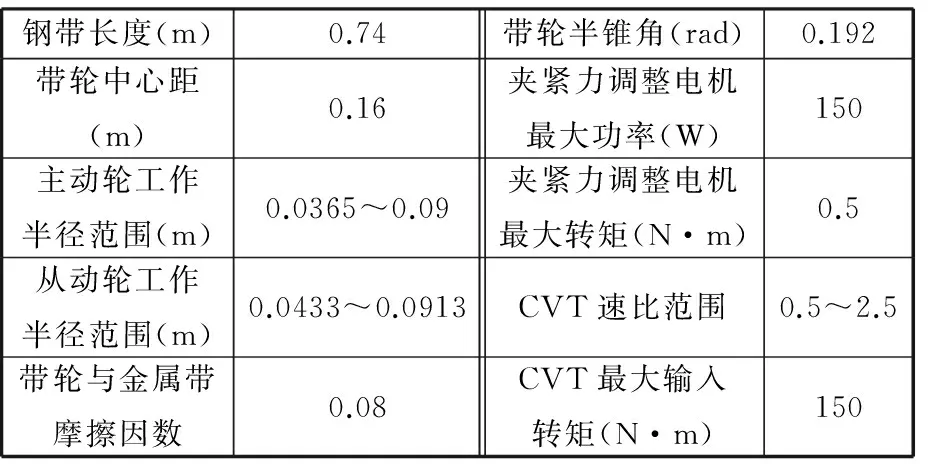
钢带长度(m)0.74带轮半锥角(rad)0.192带轮中心距(m)0.16夹紧力调整电机最大功率(W)150主动轮工作半径范围(m)0.0365～0.09夹紧力调整电机最大转矩(N·m)0.5从动轮工作半径范围(m)0.0433～0.0913CVT速比范围0.5～2.5带轮与金属带摩擦因数0.08CVT最大输入转矩(N·m)150

2　系统模型

2.1夹紧力调整电机模型

夹紧力调整电机选用普通永磁直流电机。在恒定磁场激磁条件下，建立电机运动基本方程[9]。

电压平衡方程：

(1)

式中，Uma为电动机电枢电压；Emg为反电动势；Kme为反电动势系数；ωm为电动机角速度；Ima为电枢电流；Rma为电枢回路总电阻；Lma为电枢回路总电感。

转矩平衡方程：

(2)

式中，Tm为电动机转矩；Tl为折算到电动机转轴上的负载转矩；Ta为加速转矩；Jg为折算到电动机轴上总的转动惯量。

电动机电磁转矩方程：

Tm=KmtIma

(3)

式中，Kmt为转矩系数。

式(1)～式(3)即为永磁直流电动机数学模型。

2.2夹紧力调整机构模型

从动轮夹紧力由碟簧和夹紧力调整弹簧通过其弹性变形实现对带轮的加压。考虑在不同工况下，都应该可靠地传递转矩，因此从动带轮夹紧力应满足不同工况下夹紧力的最大需求。从动轮所需夹紧力Fs可由下式计算[5]：

(4)

式中，Ti为最大输入转矩；Rp为主动带轮工作半径；α为带轮半锥角；fbp为主动带轮与金属带之间的摩擦因数。

带轮工作半径和动轮轴向位移有如下关系：

(5)

式中，Rs为从动带轮工作半径；Rp_min为主动带轮最小工作半径；Rs_max为从动带轮最大工作半径；xp为主动带轮动轮轴向位移；xs为从动带轮动轮轴向位移。

取ic=ic_max时各活动带轮的位置为坐标原点，并规定主动半带轮相向运动(沟槽变窄)为xp正向，而从动半带轮相背运动(沟槽变宽)为xs正向。通过式(4)、式(5)，可得到不同从动带轮轴向位移xs下，从动带轮所需的最大夹紧力Fsr，如图3虚线所示。按照所需夹紧力的一半确定从动轮碟簧压力，结合现有碟簧特性，获得从动轮夹紧碟簧压力Fsd随从动带轮轴向位移关系，如图3实线所示。阴影部分的压力差由夹紧力调整弹簧补充。

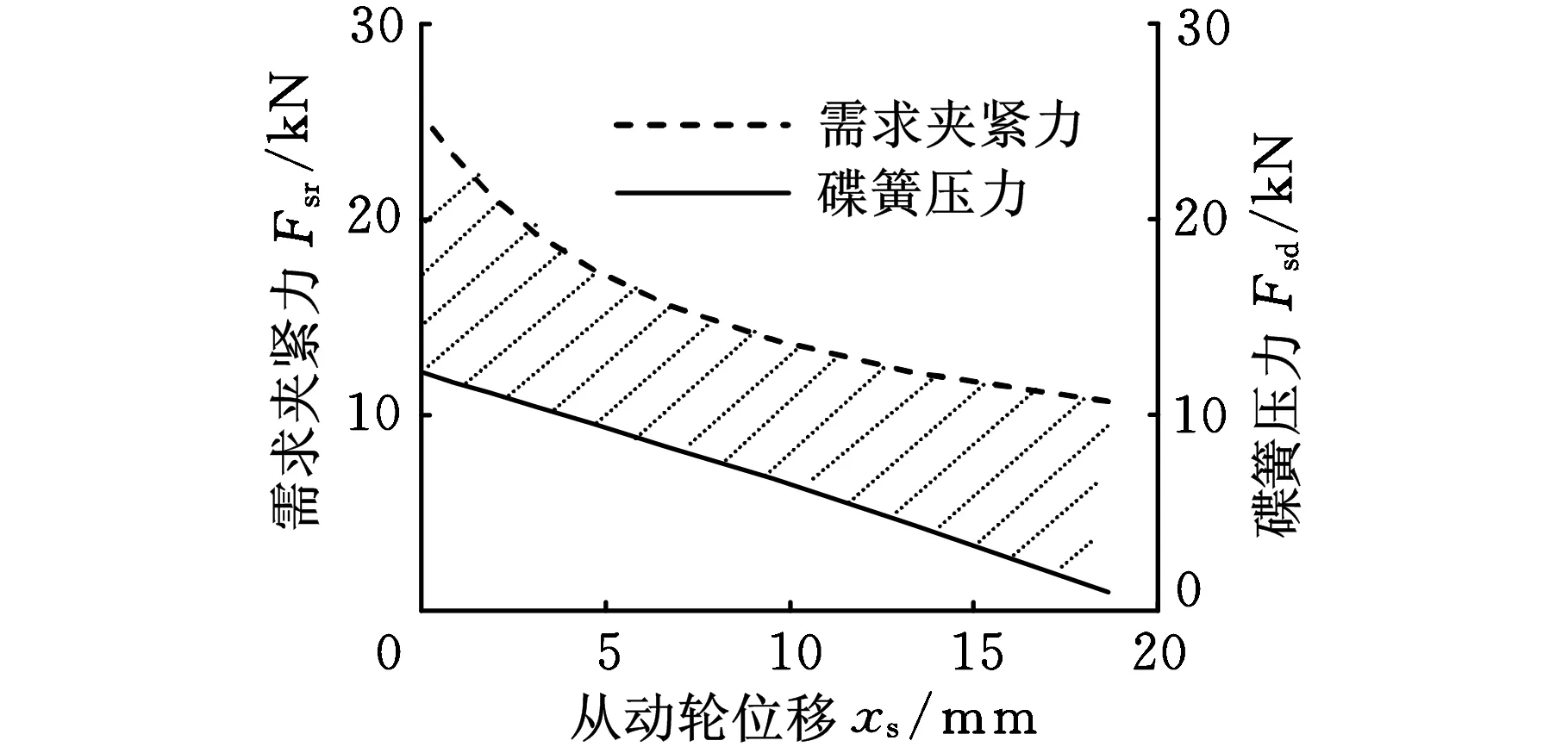
图3　从动轮最大需求夹紧力和碟簧压力随带轮轴向位移关系

由图3可以得出，需求夹紧力与碟簧夹紧力差最大值ΔFsmax为13.5kN，即夹紧力调整弹簧最大需要13.5kN的弹力。为了减轻压紧力调整电机的负荷，提高压紧力动态调整响应速度，还需要增加助力弹簧，以抵消夹紧力调整弹簧部分弹力。

定义夹紧力调整弹簧压紧力为0且从动轮工作半径最大时的位置为夹紧力调整弹簧和助力弹簧的位移原点，从动带轮工作半径减小的轴向方向为位移正方向。可得夹紧力调整弹簧的压缩量Δxj为夹紧力调整弹簧位移xj与从动轮位移xs之差，即

Δxj=xj-xs

(6)

选择合适的碟簧弹性特性线性区域[11]，可得夹紧力调整弹簧的弹性特性，如图4a所示。为了使在整个行程范围内获得比较一致的助力效果，选择碟簧弹力变化较小的区间作为助力弹簧工作区间[12]，其弹力为夹紧力调整弹簧最大弹力的一半。由于助力弹簧整体不会移动，其压缩量Δxa与助力弹簧位移xa和夹紧力调整弹簧xj位移相等。助力弹簧的弹性特性如图4b所示。

(a)夹紧力调整弹簧(b)助力弹簧弹性图4　夹紧力调整弹簧和助力弹簧弹性特性

通过以上分析，可得夹紧力调整电机负载转矩为

(7)

式中，Ls为丝杆导程；igj为夹紧力调整齿轮传动比；ηs为丝杆螺母效率。

3　仿真模型及控制策略

根据以上分析，在MATLAB/Simulink仿真平台上搭建机电控制CVT系统仿真模型。该模型由驱动轮夹紧力模块、从动轮夹紧力模块、速比变化率模块、带轮轴向速比模块、速比计算模块以及调速电机及其控制模块组成。CVT动态特性及机电控制CVT速比控制具体参见文献[13-14]。

从动轮夹紧力模块如图5所示。从动轮实际夹紧力为夹紧力碟簧弹力和夹紧力调整弹簧弹力之和。夹紧力碟簧弹力由从动轮轴向位移通过碟簧弹性特性差值获得。夹紧力调整电机角位移经丝杆螺母机构转化为直线位移xj，该位移与从动带轮轴向位移xs之差即为夹紧力调整弹簧的压缩位移Δxj，通过弹性特性差值，便可获得夹紧力调整弹簧弹力Fj。xj通过助力弹簧弹性特性差值获得助力弹簧弹力Fa，它与Fj的差值便是减速机构的负载。

由于夹紧力调节系统存在较强的非线性特性，对调节速度的控制响应精度和速度要求都比较高。仅采用位置反馈的PID速比控制难以取得令人满意的效果。需要将位置偏差、位置偏差变化率以及机构负荷作为控制输入变量，以获得较精确的目标控制速度。根据目标控制速度与实际速度的偏差来输出PWM信号，控制夹紧力调节电机。因此，采用模糊位置控制和速度PI控制

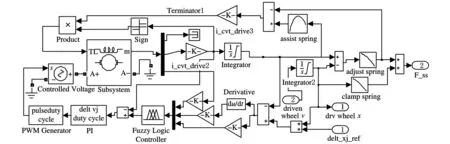
图5　夹紧力调整仿真模型

的双闭环控制方式来实现夹紧力的控制[15]。首先由输入转矩和当前速比计算出目标夹紧力Fsr。根据目标夹紧力和压紧碟簧所提供夹紧力的差值，获取夹紧力调整弹簧的目标压缩量Δxjr。由目标压缩量加上从动轮轴向位移xs，可得压紧力调整弹簧丝杆螺母端的目标位移xjr。位移采用模糊控制器进行调节。它将位置偏差Δxj，位置偏差变化率dΔxj/dt以及夹紧力调整电机负载转矩Tl作为输入量，输出量为调整弹簧目标移动速度vjr。

各变量的语言集如下：

Δxj：{负(N)、零(Z)、正(P)}

dΔxj/dt：{负大(NB)、负小(NS)、零(Z)、正小(PS)、正大(PB)}

Tl：{小(S)、中(M)、大(B)}

vjr：{负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)、正大(PB)}

若隶属度用μ表示，则各变量隶属度函数如图6所示(已作量纲一处理)。模糊控制器控制规则集见表2。

(a)位移偏差Δxj(b)位置偏差变化率

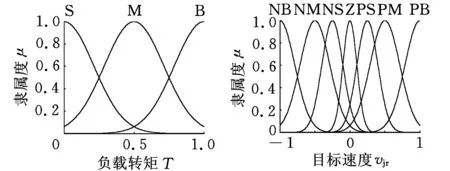
(c)夹紧力调整电机负载转矩(d)调整弹簧目标移动速度图6　各变量(已量纲一化)隶属度函数

ΔxjdΔxj/dtTlSMBNNBNBNBNBNSNBNBNBZNBNBNBPSNBNBNBPBNBNBNBZNBPMPMPMNSPSPSPMZZPSPMPSNSNSNMPBNMNMNMPNBPBPBPBNSPBPBPBZPBPBPBPSPBPBPBPBPBPBPB

vjr调节器采用PI控制器，将夹紧力调整弹簧的目标速度vjr作为输入量，输出为夹紧力调整电机的脉宽调制的占空比信号。

4　仿真分析

根据理论分析计算，获得碟簧的弹性特性，其主要特征参数见表3。仿真所用到的其余参数见表1。

图7所示为夹紧力控制的仿真结果。在0～1 s时，输入转矩为20 N·m(图7b)，CVT传动比为1.0(图7a)，从动轮需求压紧力较小(图7c)。压紧碟簧根据自身特性为从动轮提供最小压紧力(图7d)。在1～2 s时，输入转矩由20 N·m变化到150 N·m。由于输入转矩发生变化，从动轮需求的压紧力也随之发生变化(图7c中A-B段)。当需求压紧力超出实际压紧力时，控制器根据需求压紧力计算出压紧力调节电机目标转速，控制压紧力调节电机旋转，调整压紧力调整弹簧至目标行程(图7e)，从而使实际压紧力跟随需求压紧力变化(图7c)。CVT目标速比在3～4 s时，由1.0线性上升至2.2。CVT速比控制器控制速比调节电机，使CVT速比跟随目标速比变化。由于CVT速比发生变化，其需求压紧力也随之发生变化(图7c中C-D段)。压紧力控制器控制压紧力调节电机旋转，调整压紧力调整弹簧至目标位移，从而使实际压紧力跟随需求压紧力。助力弹簧提供相对稳定的弹力(图7f)，克服压紧力调整弹簧部分弹力，以减小压紧力调节电机负荷。从仿真结果来看，由输入转矩突变和CVT速比迅速变化两种情况会使需求夹紧力发生较大变化。采用本文提出的压紧力调整机构和控制策略能较好得的跟随需求压紧力的变化，满足行驶工况的需求。

表3　碟簧主要参数

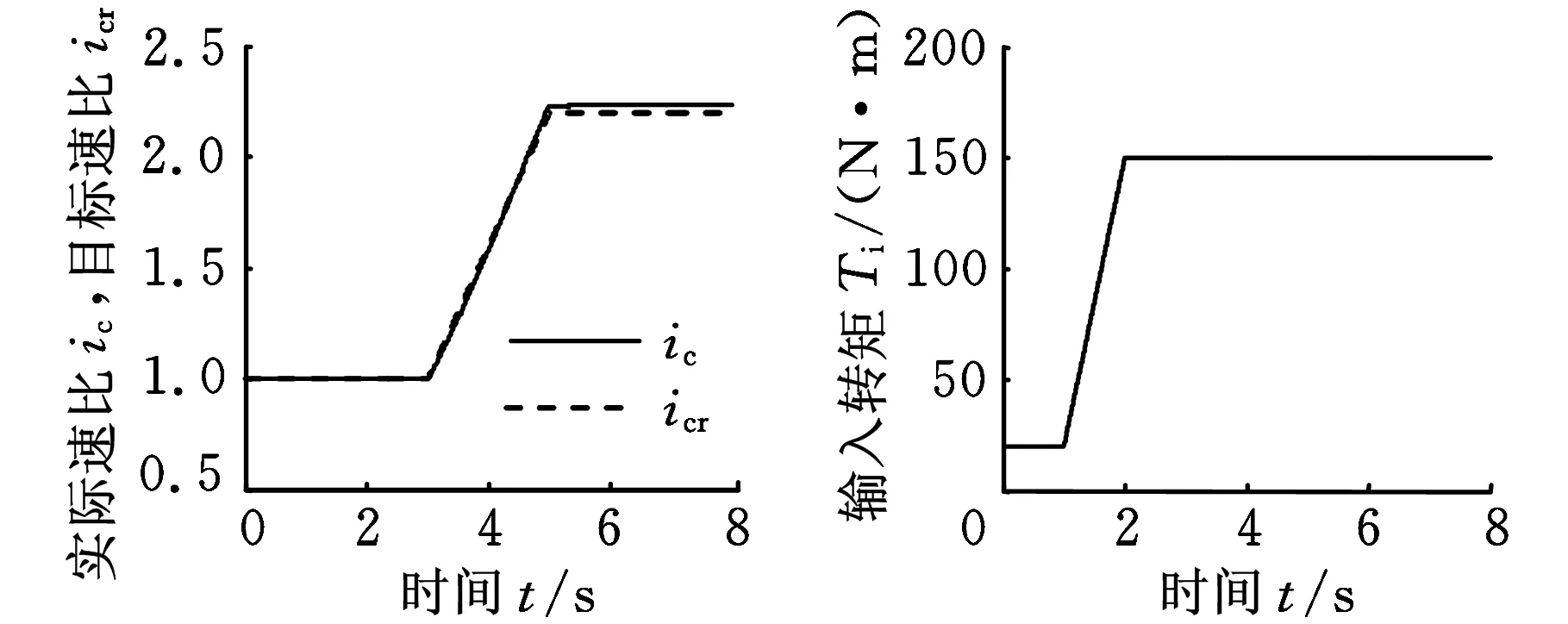
(a)速比(b)输入转矩

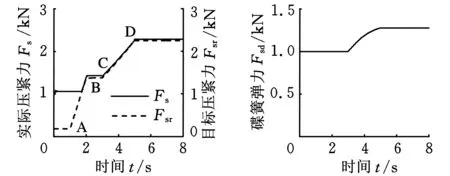
(c)从动轮压紧力(d)压紧弹簧弹力

(e)压紧力调整弹簧位移(f)调节/助力弹簧弹力图7　夹紧力控制仿真

5　结论

(1) 机电控制CVT的夹紧力采用碟簧加压，在某一速比位置只能施加固定的夹紧力。在系统运行过程中不能根据负荷调整夹紧力。

(2) 本文提出一种包含夹紧碟簧、夹紧力调整电机及其减速机构、夹紧力调整弹簧、助力弹簧的夹紧力调整调整机构，并建立数学模型。

(3)仿真结果表明，采用本文所提出的夹紧力调整机构，能较好地满足输入转矩变化和CVT速比变化所带来的需求夹紧力变化。

[1]Takashi S, Hiroyuki Y, Yoshio M, et al. Introduction of the Latest Hydraulic Control System for Automatic Transmission[C]//Proceedings of the 7th JFPS International Symposium on Fluid Power.Toyama,2008:137-142.

[2]Patric A D, Laurent T, Steven B, et al. CVT-based Full Hybrid Powertrain Offering High Efficiency at Lower Cost[J]. SAE Paper, 2010-01-1313.

[3]Zhang Lei，Hao Guili, Yang Xiumin. The Electric Vehicle Power Design and the Matching Characteristics Analysis of the Transmission System[J]. Telkomnika, 2013, 11(11): 6352-6357.

[4]程乃士，郭大忠，郝建军,等. 机械加压、电子机械控制汽车无级变速器[P]. 中国专利：200620110951.5，2007-10-31.

[5]薛殿伦, 杨凯, 程金接. 金属带式无级变速器夹紧力的分析与研究[J]. 汽车工程, 2010,34(10): 923-927.

Xue Dianlun, Yang Kai，Cheng Jinjie. Analysis and Study on the Clamping Force of Metal V-belt CVT[J]. Automotive Engineering, 2010,34(10):923-927.

[6]van der Meulen S, de Jager B, Veldpaus F, et al. Improving Continuously Variable Transmission Efficiency with Extremum Seeking Control[J]. IEEE Transactions on Control Systems Technology, 2012,20(5):1376-1383.

[7]Rahman A, Sharif S B, Hossain A, et al.Kinematics and Nonlinear Control of an Electromagnetic Actuated CVT System for Passenger Vehicle[J]. Journal of Mechanical Science and Technology,2012, 26(7):2189-2196.[8]van der Noll E, van der Sluis F, van Dongen T, et al. Innovative Self-optimising Clamping Force Strategy for the Pushbelt CVT[J]. SAE International Journal of Engines，2009,2(1):1489-1498.

[9]李光友,王建民，孙雨萍.控制电机[M]. 北京：机械工业出版社， 2009.

[10]程乃士. 汽车金属带式无级变速器:CVT原理和设计[M]. 北京：机械工业出版社，2008.

[11]邱梅开. 碟形弹簧弹性特性的分析[J]. 农业工程学报, 1994, 10(3):83-87.

Qiu Meikai. Elastic Characteristic of Disk Spring[J].Transactions of the Chinese Society of Agricultural Engineering,1994, 10(3):83-87.

[12]易先中, 张传友, 严泽生. 碟形弹簧的力学特性参数研究[J]. 长江大学学报(自然科学版),2007,4(4)：99-101,140.

Yi Xianzhong, Zhang Chuanyou, Yan Zesheng. Research onMechanical Properties of Disk Spring[J]. Journal of Yangtze University (Natural Science Edition) Sci. & Eng., 2007, 4(4)：99-101,140.

[13]Carbone G, Mangialard L, Bonsenb B, et al. CVT Dynamics: Theory and Experiments[J]. Mechanism and Machine Theory, 2007,42(4):409.

[14]叶明，程越. 电驱动无级自动变速传动动态控制研究[J]. 机械传动, 2011，35(2)：9-12.

Ye Ming, Cheng Yue.Study on Dynamic Control of Continuously Variable Transmission Driven by DC Motor[J]. Journal of Mechanical Transmission, 2011，35(2)：9-12.

[15]张传伟,郭卫.直流电机双闭环调速系统仿真研究[J]. 机床与液压, 2005(2)：128-129.

Zhang Chuanwei, Guo Wei. Simulation Research on the Speed Governing System of DC Motor[J]. Machine Tool & Hydraulics,2005(2)：128-129.

(编辑郭伟)

Performance Analysis of Variable Clamping Force Actuator of EMCVT

Ye MingLi XinLuo Yong

Key Laboratory of Advanced Manufacturing Techniques for Automobile Parts,Ministry of Education,Chongqing University of Technology,Chongqing,400054

EMCVT was driven by direct current motor. It was more efficient， had less parts and better control performance than that driven by electric-hydraulic system. So far the clamping force of EMCVT could not be varied with input torque. A new type of actuator where the control clamping force was put forward. Mathematical model of clamping force control actuator was built and a dual closed loop controller with fuzzy logic control and PI control was designed. Simulation results show that control performance of clamping force actuator and control strategies are good and meet the requirements of clamping force while system running.

electric-mechanic continuously variable transmission(EMCVT); variable clamping force; control; simulation

2013-11-12

国家自然科学基金资助项目(51275549); 重庆市科委自然科学基金资助项目(cstc2012jjA60003)；重庆市教委科学技术研究资助项目(KJ120830)

U463.2DOI：10.3969/j.issn.1004-132X.2015.03.020

叶明，男，1976年生。重庆理工大学汽车零部件先进制造技术教育部重点实验室副研究员、博士。主要研究方向为车辆动力传动系统综合控制。获市科学技术进步一等奖、二等奖各1项，发表论文25篇。 李鑫，男，1969年生。重庆理工大学汽车零部件先进制造技术教育部重点实验室实验师。罗勇，男，1981年生。重庆理工大学汽车零部件先进制造技术教育部重点实验室助理研究员、博士。