求解液压阀块加工车间调度的多作用力微粒群算法
2015-10-29陈东宁张瑞星姚成玉茜彦辉
陈东宁 张瑞星 姚成玉 茜彦辉
1.燕山大学河北省重型机械流体动力传输与控制重点实验室,秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,0660043.燕山大学河北省工业计算机控制工程重点实验室,秦皇岛,066004
求解液压阀块加工车间调度的多作用力微粒群算法
陈东宁1,2张瑞星1,2姚成玉3茜彦辉1,2
1.燕山大学河北省重型机械流体动力传输与控制重点实验室,秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,0660043.燕山大学河北省工业计算机控制工程重点实验室,秦皇岛,066004
为有效地解决液压阀块加工车间调度问题,考虑工序间和机器间的约束关系,以最大完成时间最小为目标,给出了液压阀块加工车间调度优化模型。为平衡算法的全局和局部搜索能力,提出了多作用力微粒群(MFPSO)算法,采用多作用力阶段性搜索策略,将搜索过程划分为前期、中期、后期3个阶段,并对应构造单一斥力、平衡引斥力、单一引力3种作用力规则,在不同搜索阶段采用不同的作用力规则,提高了算法的搜索机制和寻优性能。将MFPSO算法用于求解液压阀块加工车间调度问题,利用矩阵变量来处理约束条件,给出了一种基于矩阵的微粒编码、解码方法。通过液压阀块加工车间调度优化实例,将MFPSO算法与微粒群算法、中值导向微粒群算法、扩展微粒群算法、蚁群算法进行了对比,结果表明,提出的MFPSO算法结果最优,从而验证了该算法的有效性。
液压阀块加工车间调度;微粒群算法;作用力规则;MFPSO算法
0 引言
生产调度本质上属于复杂的优化问题,具有大规模、非线性、强约束、多极值、多目标等复杂性。高效的优化技术与调度方法的研究与应用,是提高生产效率和经济效益的核心环节。优化技术与调度方法可以归结为3种类型:精确求解算法[1]、启发式方法[2]和基于人工智能的方法[3]。
近年来基于人工智能的方法凭借其渐进式寻优、并行式搜索、适者生存式进化、通用性强、易于与其他算法结合等优势,备受学者的青睐,并被应用于解决调度问题,其中常用的智能算法包括蚁群(ant colony optimization,ACO)算法[4]、微粒群(particle swam optimization,PSO)算法[5]、遗传算法[6]、差分进化算法[7]等。其中,PSO算法作为一种高效的群体智能优化算法,已成功应用于求解各种生产调度问题,但它存在易陷入局部最优、出现早熟等不足。
微粒间的作用力决定了微粒速度的方向和大小,是平衡微粒全局和局部搜索的关键因素。标准PSO算法的作用力规则中仅考虑个体最优微粒和全局最优微粒对当前微粒的引力,这是导致算法陷入局部最优的内在缺陷,因此,一些学者从以下4个侧面对PSO算法的作用力规则进行了改进:①调整引力大小。例如,采用线性递减的惯性权重策略、基于模糊规则动态调整惯性权重的策略来调整微粒间引力大小[8];引入收缩因子概念,根据微粒适应度来动态改变收缩因子大小,从而改变当前微粒所受的引力大小[9];动态调整加速因子[10];将自适应理论与PSO算法结合,自适应地调整惯性权重,从而调整个体最优微粒和全局最优微粒对当前微粒的引力大小[11]。②增添引力。例如,同时考虑个体最优微粒和具有寿命周期的全局最优微粒对当前微粒的引力[12];添加当代最优微粒对当前微粒的引力[13];考虑中间适应度微粒对当前微粒引力的中值导向PSO(median-oriented PSO,MPSO)算法[14];考虑距离当前微粒最近的微粒的引力[15];将标准PSO算法中个别微粒对当前微粒的引力扩展为所有个体最优微粒的引力[16]。③增添斥力。例如,引入种群多样性函数[17];根据种群多样性自适应改变全局最优微粒的引力和斥力[18];考虑适应度变差的微粒对当前微粒的斥力[19]。④增添引力和斥力。例如,扩展PSO(extended PSO,EPSO)算法将个体最优和全局最优微粒对当前微粒的引力扩展为所有微粒对当前微粒的引力、斥力[20]。
上述算法可从避免算法早熟收敛、保证种群多样性、提高收敛速度和搜索精度等某些侧面改进PSO算法的性能,但这些算法仅考虑单种作用力规则,使微粒间的作用机制相对单一,不能同时兼顾对算法的种群多样性、收敛速度等性能要求。为此,本文考虑在不同搜索阶段采用不同的作用力规则,丰富微粒间的作用力,平衡算法的全局和局部搜索能力,提出多作用力PSO(multi force PSO,MFPSO)算法,进而将其用于求解液压阀块加工车间调度问题,以寻找最佳的调度方案。
1 液压阀块加工车间调度优化模型
1.1液压阀块加工工艺
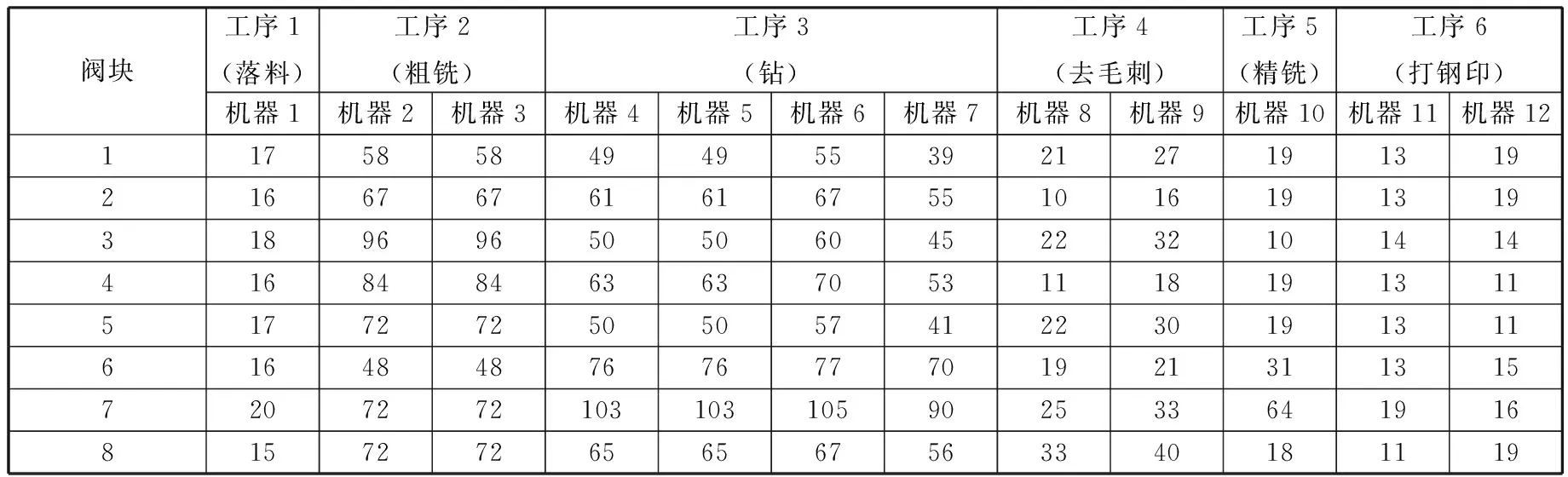
某公司液压阀块加工车间主要为动力站中的泵站单元和阀台单元提供用于安装各种液压元件并实现各元件油路连通的阀块,这些动力站广泛应用于生产加工和制造业中,如冶金、矿山、船厂等重工业设备,垃圾回收及处理设备,机床、压力机、水利工程、纸浆和造纸机械等。为整套设备提供动力源的液压动力站能够安全平稳地工作,是这些设备安全、可靠运行的基础,因此对动力站中液压阀块的加工质量和工艺控制有较高的要求。该加工车间有锯床1台、铣床3台(含数控铣床1台)、钻床4台(含数控钻床1台)、去刺机2台、打码机2台。为实现上述液压阀块的加工工艺性要求,该公司制订了其特有的液压阀块加工工艺流程,每个阀块均需经过6道工序加工:落料、粗铣、钻、去毛刺、精铣、打钢印,如图1所示。
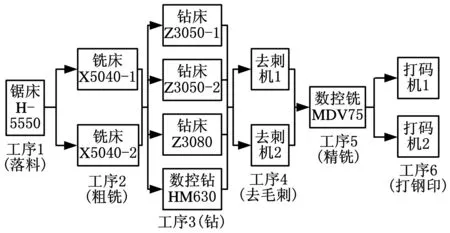
图1 液压阀块加工工艺流程
该车间还设有专门的液压阀块装配区域,从而形成了液压阀块从加工到装配的生产流水线。该车间加工的液压阀块最长达2500 mm,最重达5 t,并能够保证液压阀块所需的加工工艺要求。
1.2调度优化模型
该液压阀块加工车间调度问题具有流水作业特征,同时工序2、3、4、6上存在并行机加工的特点,由此可见,该问题属于混合流水车间调度问题(hybrid flow-shop scheduling problem,HFSP)。HFSP可描述为:nM个工件要经过s道工序以完成加工,每道工序至少有一台机器进行加工且至少有一道工序存在并行机器,同一道工序上各机器的处理性能可相同也可不同,各工件的每道工序可在任意一台并行的机器上加工,已知工件在各工序相应机器上的处理时间,要求确定所有工件的排序以及每道工序上机器的分配情况,使得调度指标(这里取为最大完成时间)最小。
结合现场工艺作如下假设:工件一旦开始加工便不可中断;一台机器同一时刻只能加工一个阀块;一个阀块同一时刻只能在一台机器上加工;在并行加工工艺阶段,阀块可在并行机器的任意一台机器上加工。考虑各机器的调机时间,以完成nM个阀块加工的最大完成时间最小为目标,给出该阀块加工车间调度优化模型如下:
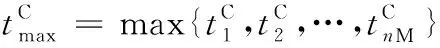
(1)
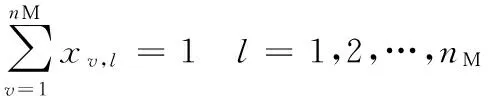
(2)
(3)
(4)
u=1,2,…,s
(5)
v=1,2,…,nM;u=1,2,…,s-1
k=1,2,…,mu;k′=1,2,…,mu+1
(6)
v=1,2,…,nM;l=1,2,…,nM-1;k=1,2,…,m1
(7)
l1,l2=1,2,…,nM;l1≤l2
u=1,2,…,s;k,k′=1,2,…,mu
其中
(8)
(9)
(10)
(11)
上述调度优化模型中,式(2)和式(3)确保了每个优先级位置与阀块间一一对应;式(4)使得对于每道工序每个阀块只能在一台机器上加工;式(5)表示了同一阀块不同工序间的先后制约关系;式(6)表示第一道工序上调度排列中排位越前的阀块开始加工时间越早;式(7)实现了同道工序分配在同一机器上的阀块排位靠后的必须等靠前的加工完成后才可进行加工,当处于不同位置的阀块不在同道工序的同一机器上加工时,L数值较大以保证不等式恒成立。
2 多作用力微粒群算法
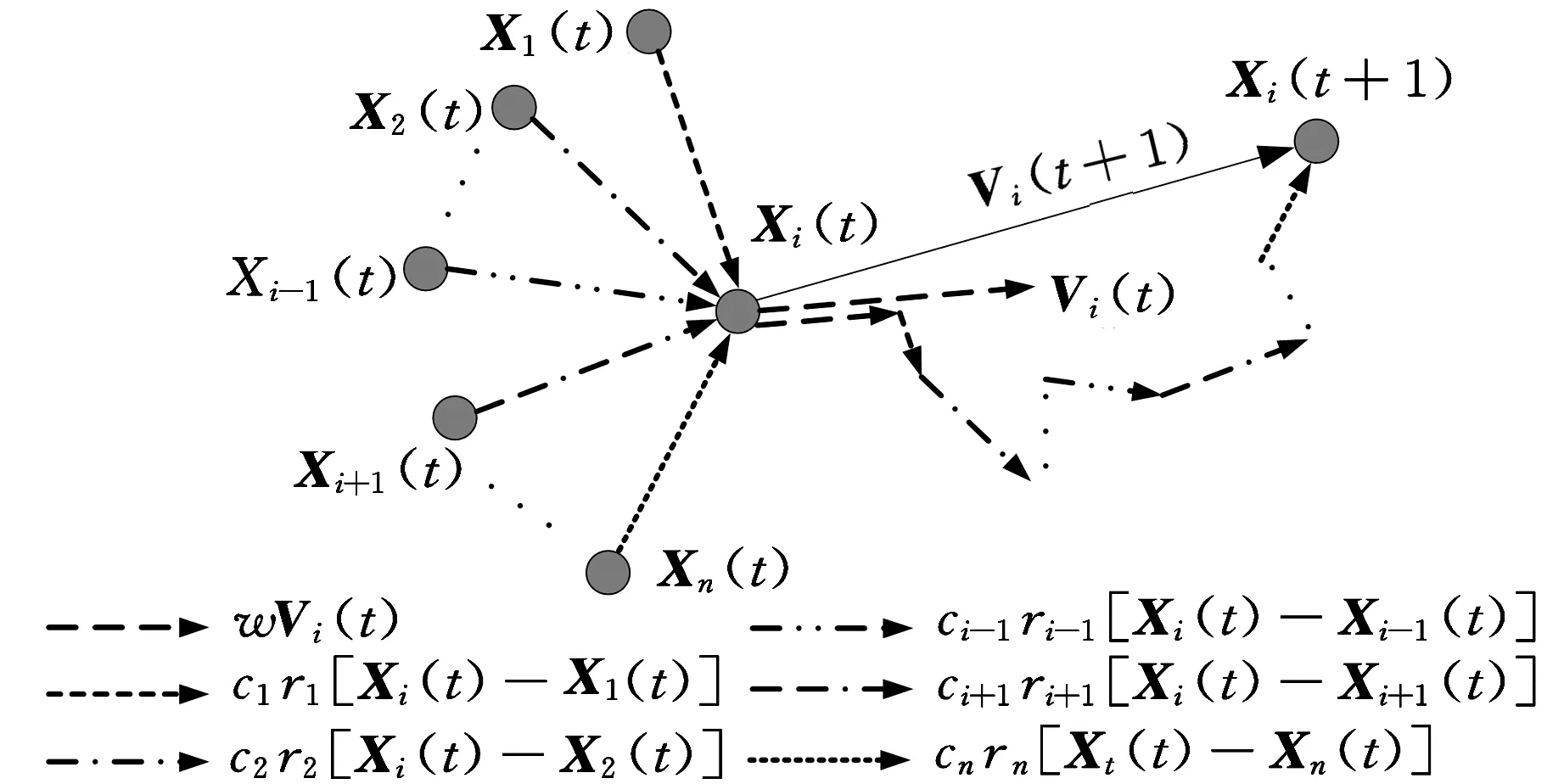
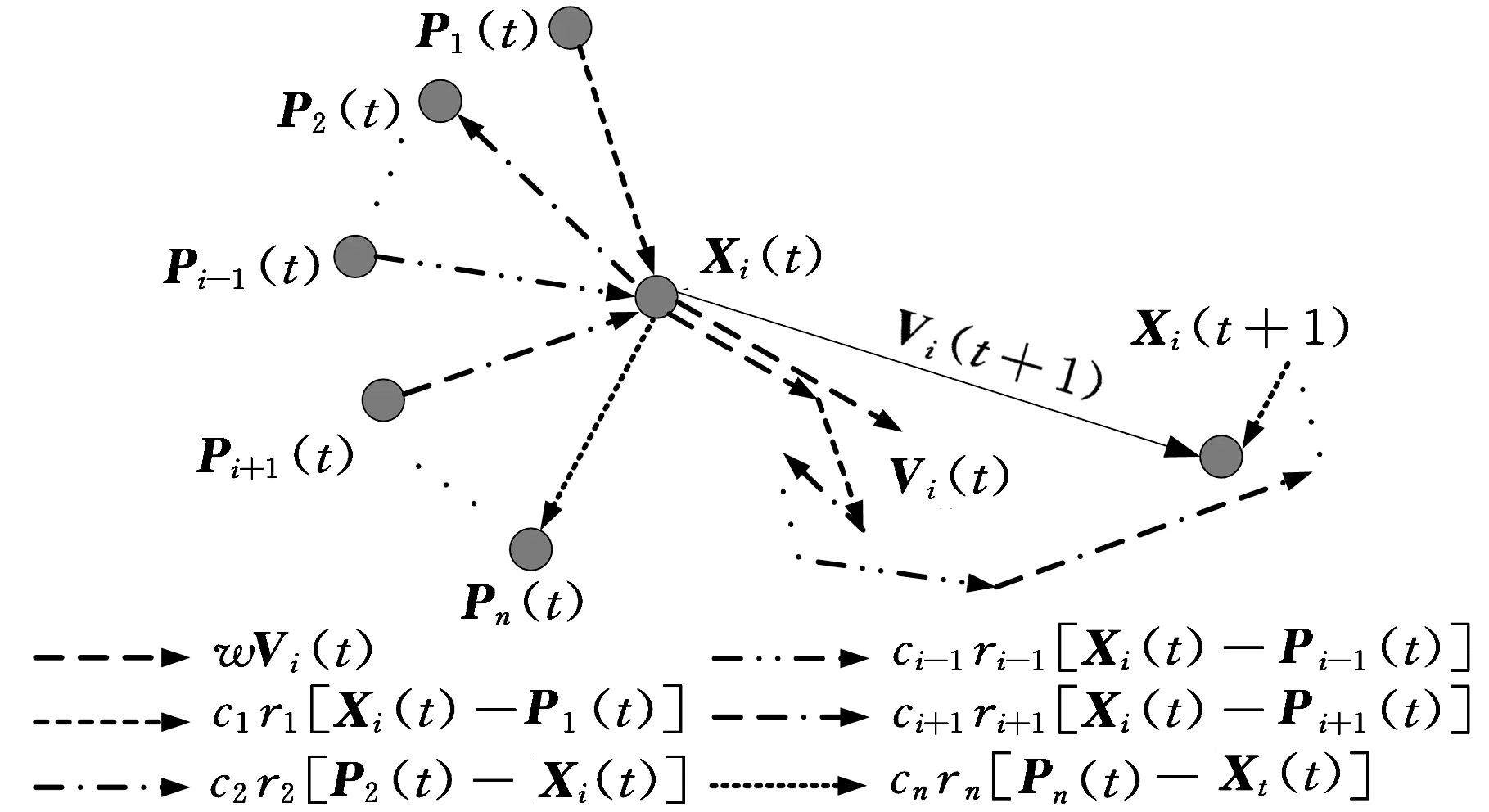
多作用力微粒群(MFPSO)算法的基本思想如下:采用多作用力阶段性搜索策略,将搜索过程划分为前期、中期、后期3个阶段,考虑微粒间作用力,借鉴拟态物理学中的引斥力思想,分别构造单一斥力、平衡引斥力、单一引力3种作用力规则,在不同搜索阶段采用不同的作用力规则,通过计算当前微粒所受的作用力,更新微粒的速度和位置,根据微粒的适应度更新个体最优微粒和全局最优微粒。
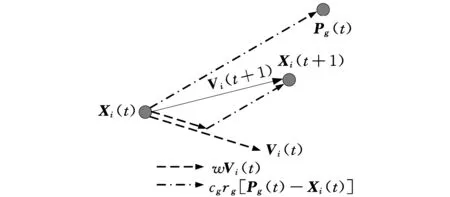
前期,考虑微粒间的排斥作用,构造单一斥力的作用力规则,使微粒受所有微粒的斥力作用,以增强微粒群的种群多样性,提高算法的全局搜索能力;中期,同时考虑微粒间的吸引和排斥作用,构造平衡引斥力的作用力规则,使微粒受到比其适应度好的个体最优微粒的引力和比其适应度差的个体最优微粒的斥力作用,以保持微粒群的种群多样性,平衡算法的全局和局部搜索能力;后期,考虑全局最优微粒的吸引作用,构造单一引力的作用力规则,使微粒向全局最优微粒靠近,以增强算法的局部搜索能力,提高收敛速度。
2.13种作用力规则的构造
假设在n维搜索空间中,微粒群的种群规模为N,对于任意微粒i(i=1,2,…,N),第t代微粒i的位置矢量为Xi(t)=(xi1(t),xi2(t),…,xi n(t)),速度矢量为Vi(t)=(vi1(t),vi2(t),…,vi n(t)),其个体最优微粒的位置矢量为Pi(t)=(pi1(t),pi2(t),…,pi n(t));对于整个微粒群,第t代全局最优微粒g的位置矢量为Pg(t)=(pg1(t),pg2(t),…,pg n(t))。
(1)单一斥力的作用力规则。微粒j对微粒i的斥力为
xi d(t)-xj d(t)j∈N
(2)平衡引斥力的作用力规则。比微粒i适应度好的个体最优微粒对微粒i的引力为
pj d(t)-xi d(t)j∈Bi(t)
比微粒i适应度差的个体最优微粒对微粒i的斥力为
xid(t)-pjd(t)j∈Wi(t)
其中
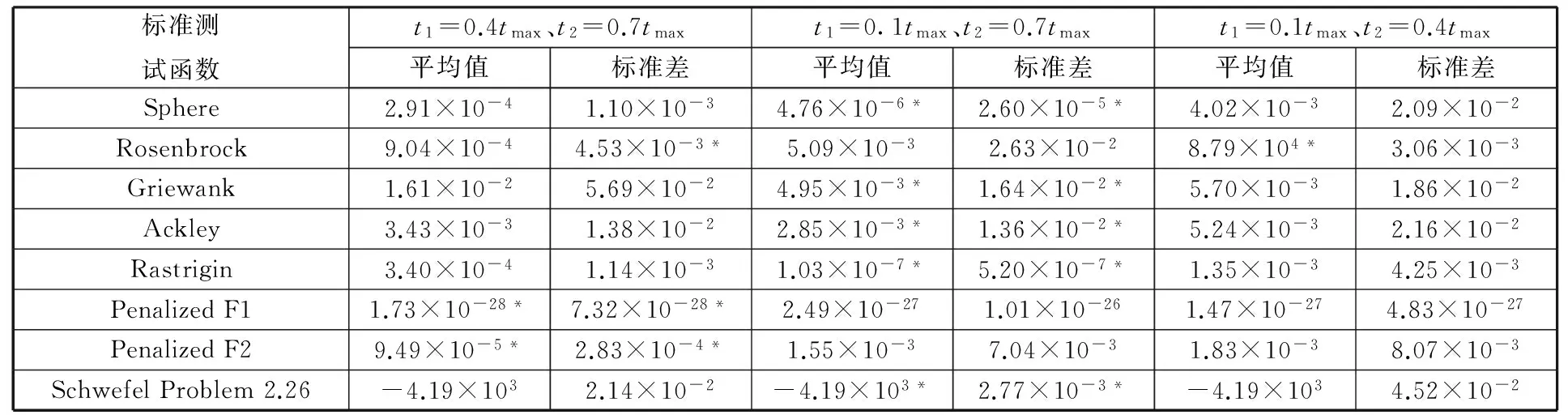
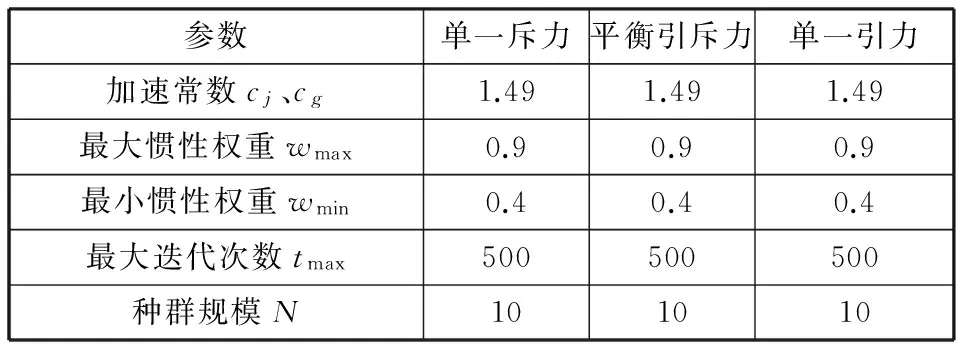
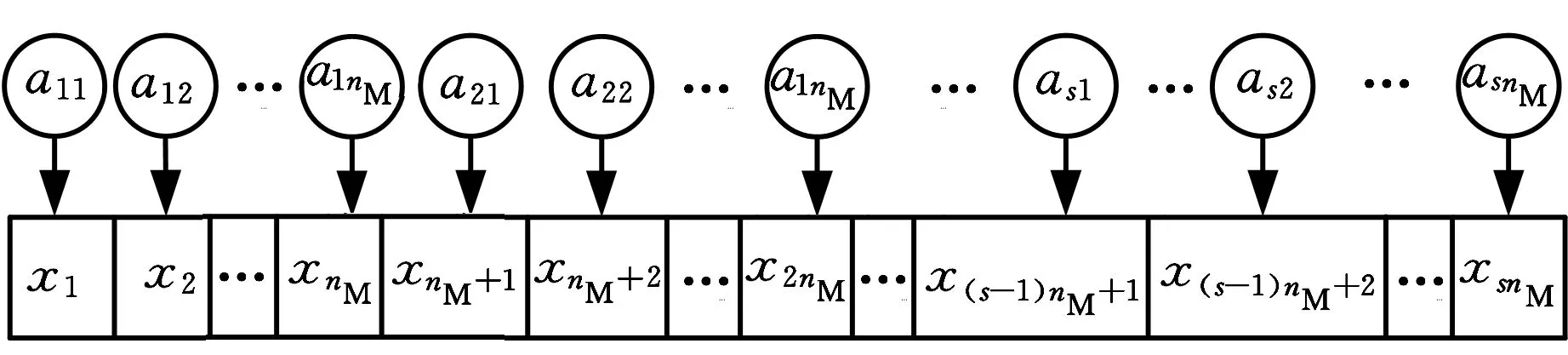
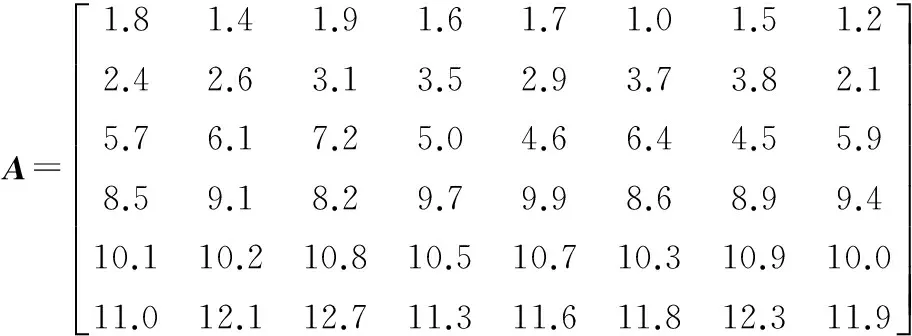
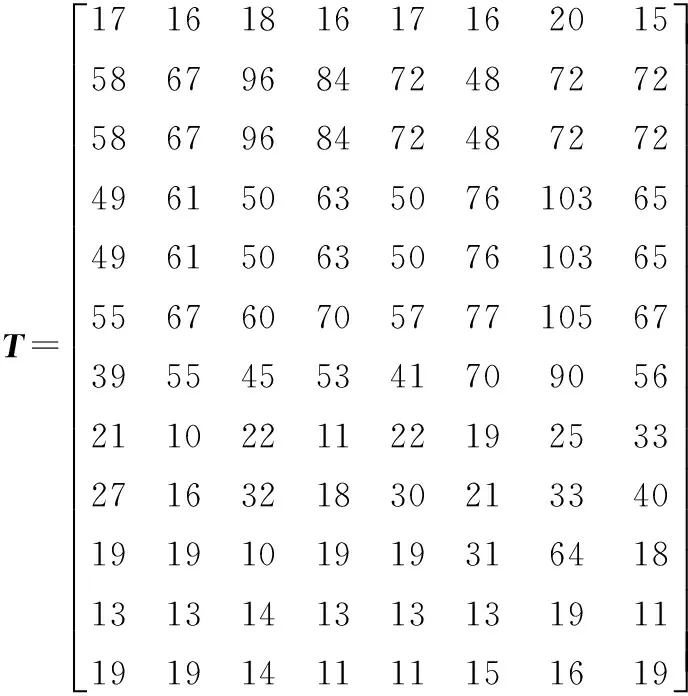
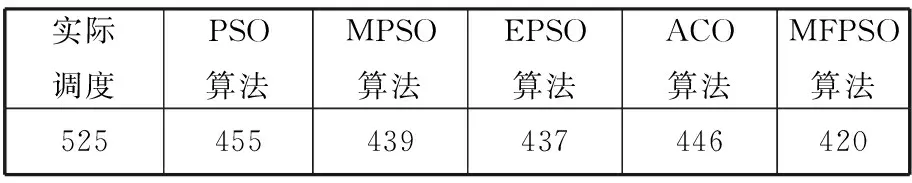
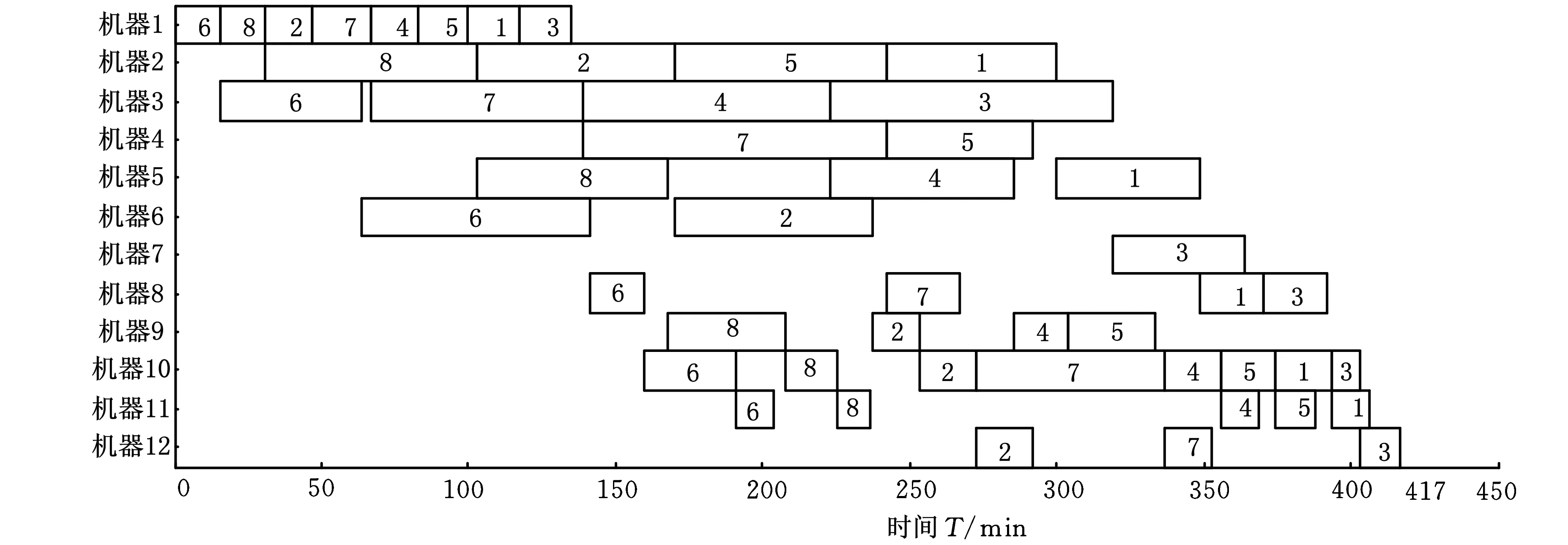
Bi(t)={j|f(Pj(t)) Wi(t)={j|f(Pj(t))≥f(Xi(t))∀j∈N} (3)单一引力的作用力规则。全局最优微粒g对微粒i的引力为 pg d(t)-xid(t) 上述相关变量中,xj d(t)为第t代微粒j的第d维位置;pj d(t)为第t代微粒j的个体最优微粒的第d维位置;Bi(t)为第t代比微粒i适应度好的个体最优微粒的集合;Wi(t)为第t代比微粒i适应度差的个体最优微粒的集合;f(·)为适应度函数;pgd(t)为第t代全局最优微粒g的第d维位置。 2.2微粒的速度和位置更新 MFPSO算法的速度和位置更新公式为 (12) xid(t+1)=xid(t)+vid(t+1) (13) 式中,vid(t)为第t代微粒i的第d维速度;w为惯性权重;α、β、γ为前期、中期、后期3阶段搜索的切换系数;cj、cg为加速常数;rj、rg为(0,1)区间互相独立的随机数。 惯性权重w可由下式求得: (14) 式中,wmax为惯性权重的最大值;wmin为惯性权重的最小值;tmax为最大迭代次数。 前期、中期、后期3个阶段搜索的切换系数α、β、γ可分别由下式求得: (15) (16) (17) 式中,t1为前期向中期搜索切换时的切换因子;t2为中期向后期搜索切换时的切换因子。 (a)基于单一斥力的前期搜索 (b)基于平衡引斥力的中期搜索 (c)基于单一引力的后期搜索图2 MFPSO算法微粒迭代更新的过程 图2对MFPSO算法中微粒迭代更新的过程进行了形象的描述。图2a~图2c分别为MFPSO算法结合微粒速度更新公式(式(12))和位置更新公式(式(13))进行前期、中期、后期搜索的加权求和示意图。微粒的移动方向由两部分组成:①微粒i自身原有的速度Vi(t),并由惯性权重w决定其相对重要性;②其他微粒j(j=1,2,…,i-1,i+1,…,N)对微粒i的作用力:基于单一斥力的前期搜索时,微粒i受到的作用力为其他微粒j的斥力Xi(t)-Xj(t)的矢量和;基于平衡引斥力的中期搜索时,微粒i受到的作用力为比自身适应度好的个体最优微粒j(j∈Bi(t))的引力Pj(t)-Xi(t)和比自身适应度差的个体最优微粒j(j∈Wi(t))的斥力Xi(t)-Pj(t)的矢量和;基于单一引力的后期搜索时,微粒i受到的作用力为全局最优微粒g的引力Pg(t)-Xi(t)。作用力的相对重要性由对应的加速常数c和随机数r决定。 2.3切换因子对MFPSO算法的影响 由于本文所提的MFPSO算法的特征是基于不同作用力规则的阶段性搜索,因此,不同的切换因子t1和t2会影响各作用力在算法的整个搜索过程中所占比重,进而影响算法的寻优性能。为寻求一组较好的切换因子,首先,测试每一种作用力单独作用下,算法出现进化停滞时的迭代次数;然后,根据上述测试出的迭代次数t与最大迭代次数tmax的关系来设置几组切换因子,通过测试分析来确定一组相对最佳的切换因子。 本文选取表1所示的8个被广泛应用于评价优化算法性能的标准测试函数,测试每一种作用力规则单独作用下算法的寻优能力,参数设置如表2所示,在每种作用力下算法独立运行30次。测试发现,基于单一斥力规则、平衡引斥力规则、单一引力规则,算法分别在t=0.1tmax、t=0.3tmax、t=0.3tmax代时进化已出现停滞现象。为使3个搜索阶段能够充分发挥作用,选取3组切换因子t1、t2进行测试:①t1=0.4tmax、t2=0.7tmax,加强前期搜索作用,增强种群多样性;②t1=0.1tmax、t2=0.7tmax,加强中期搜索作用,平衡全局和局部搜索;③t1=0.1tmax、t2=0.4tmax,加强后期搜索作用,提高收敛速度。再次进行标准测试函数测试,算法运行30次求平均值和标准差,3组切换因子下MFPSO算法的优化结果如表1所示,表中数字右上方标有“*”的数值为对应数据的最优值。由表1可知,t1=0.1tmax、t2=0.7tmax时,对于大多数测试函数而言,MFPSO算法所得的结果相对最优。这表明,在考虑到前期、后期搜索作用的同时增强中期搜索,可以使MFPSO算法性能较优。 表1 不同切换因子下MFPSO算法的优化结果 表2 参数设置 2.4MFPSO算法的执行步骤 MFPSO算法的流程如图3所示。 (1)初始化微粒群。随机初始化微粒的速度和位置,即微粒群中每个微粒的每一维速度和位置分别在[vmin,vmax]和[xmin,xmax]区间内随机产生;计算微粒的适应度;确定任意微粒j(∀j∈N)的个体最优微粒和全局最优微粒g。 (2)基于单一斥力的前期搜索。计算所有微粒对当前微粒i的斥力,利用式(6)和式(7)更新微粒的速度和位置;计算微粒的适应度;更新任意微粒j的个体最优微粒和全局最优微粒g。 (3)判断前期搜索是否结束,若迭代次数t (4)基于平衡引斥力的中期搜索。计算比微粒i适应度好的个体最优微粒对当前微粒i的引力和比微粒i适应度差的个体最优微粒对当前微粒i的斥力,利用式(6)和式(7)更新微粒的速度和位置;计算微粒的适应度;更新任意微粒j的个体最优微粒和全局最优微粒g。 (5)判断中期搜索是否结束,若迭代次数t (6)基于单一引力的后期搜索。计算全局最优微粒g对当前微粒i的引力,利用式(6)和式(7)更新微粒的速度和位置;计算微粒的适应度;更新任意微粒j的个体最优微粒和全局最优微粒g。 (7)判断终止条件,若t=tmax,则执行(8),否则返回(6)。 (8)输出优化结果。 采用MFPSO算法求解液压阀块加工车间调度问题。首先,利用矩阵变量来处理约束条件,对微粒进行编码;然后,利用MFPSO算法不断地搜索并更新全局最优解;最后,对微粒进行解码,求得最优的调度方案。编码,即微粒位置的表示方式,本文利用矩阵来对微粒进行编码,用列表示液压阀块,用行表示工序,利用矩阵的元素来表示机器,利用矩阵元素的位置关系来表示工序间的约束关系,为了扩大微粒的搜索空间以求得最优解,采取随机产生实数的编码方法,以均等的机会选择机器。由于微粒在速度-位置的迭代过程中是连续的,为避免产生非法解,本文采取了一种特殊的解码方式,得到选择机器矩阵,然后利用液压阀块在各机器上加工时间的数据表生成加工时间矩阵,按照一定的加工排序规则,得到完成时间矩阵。利用PSO算法以最大完成时间为适应度函数,进行迭代寻优最终产生使得该流水线加工完成时间最短的调度方案及其甘特图。 3.1问题描述 现有8个液压阀块要加工,每个阀块均需经过6道工序加工:落料、粗铣、钻、去毛刺、精铣、打钢印,各机器按照工序顺序依次编号,液压阀块在各机器上的加工时间见表3。采用MFPSO算法求解,以合理地分配每道工序的机器,确定同一台机器上各阀块加工的顺序,寻求完成所有阀块加工的最大完成时间最小的最优调度方案。 表3 液压阀块在各机器上的加工时间 min 3.2编码矩阵A 假设要加工nM个阀块,每个阀块都要依次经过s道加工工序,每道工序的机器数为mu(u=1,2,…,s),对所有机器按照加工工序依次排序编号,可构造一个s×nM维的编码矩阵A: (18) 根据上述编码方法对微粒进行编码:每个微粒由s个小段组成,每个小段包括nM个数值,每个微粒的长度为s×nM,从而形成了nM个阀块完成s道工序的一个调度方案。以元素au v为自变量,微粒i的位置矢量Xi可表示为 Xi=(x1,x2,…,xnM,xnM+1,xnM+2,…,x2nM,…, x(s-1)nM+1,x(s-1)nM+2,…,xsnM)= (a11,a12,…,a1nM,a21,a22,…, a2nM,…,as1,as2,…,asnM) 它对应着一个编码矩阵A,代表了一个可行的调度方案。 采用图示的方式描述微粒编码中自变量auv与位置矢量Xi的元素xi之间的对应关系,如图4所示。 图4 微粒编码图示 对于上述液压阀块加工车间调度问题,采用MFPSO算法进行求解,其参数设置如下:种群规模N=20,函数维数n=8×6=48,最大迭代次数tmax=500,切换因子t1=50、t2=350,惯性权重wmin=0.4、wmax=0.9,加速常数cj=cg=1.49。微粒不断地搜索并更新全局最优解,则经过500代搜索后得到全局最优解,其编码矩阵A如下: (19) 有编码必有解码,要得到最优的调度方案,需对上述编码矩阵A进行解码,解码过程分为两步:首先,对编码矩阵A取整,并生成选择机器矩阵S;其次,按照先来先加工的规则,确定阀块的加工顺序,并生成完成时间矩阵TC。 3.3选择机器矩阵S 对式(19)的编码矩阵A中各个元素au v分别向下取整,得到矩阵B: (20) 由编码矩阵A可知,矩阵B中的行表示各工序,列表示要加工的阀块,根据各工序上的机器编号规则,由矩阵B的列可得到各阀块与机器的对应关系,例如,第1列的含义为:阀块1的6道工序分别在机器1、2、5、8、10、11上加工;第2列的含义为:阀块2的6道工序分别在机器1、2、6、9、10、12上加工。然后,将6行(6道工序)8列(8个阀块)的矩阵B按列扩展成12行(12个机器)8列的选择机器矩阵S,根据各阀块在相应工序是否选择了该机器置矩阵中相应元素的值为1或0,1表示选取该机器,0表示未选取,例如,根据矩阵B的第1列,将选择机器矩阵S第1列的第1、2、5、8、10、11行取1,其余各行取0,依次类推,得到选择机器矩阵S: (21) 3.4完成时间矩阵的生成 3.4.1加工时间矩阵TP 将表3阀块在各机器上的加工时间表示为矩阵T: (22) 为提取各阀块在其实际使用机器上的加工时间,屏蔽没有实际使用的机器,将矩阵T与选择机器矩阵S点乘得到加工时间矩阵TP: (23) 它表示了各阀块的各道工序在其选择的机器上的加工时间。 3.4.2确定阀块的加工顺序 按照先来先加工的规则,确定阀块的加工顺序。当出现int(au v)=int(au z)且v≠z时,表明阀块v和z在同一台机器上加工同一道工序u,这时,如果是第一道工序(u=1),则按照元素a1v的升序来加工阀块;如果不是第一道工序(u>1),则根据每个阀块的前一道工序完成时间的早晚来确定其加工顺序,前一道工序先完成的阀块先加工;如果完成时间相同,则也按照au v的升序来加工。 根据上述阀块加工顺序规则,可确定同一机器上阀块的加工先后顺序如下:机器1加工阀块6、8、2、7、4、5、1、3的第1道工序;机器2加工阀块8、2、5、1的第2道工序;机器3加工阀块6、7、4、3的第2道工序;机器4加工阀块7、5的第3道工序;机器5加工阀块8、4、1的第3道工序;机器6加工阀块6、2的第3道工序;机器7加工阀块3的第3道工序;机器8加工阀块6、7、1、3的第4道工序;机器9加工阀块8、2、4、5的第4道工序;机器10加工阀块6、8、2、7、4、5、1、3的第5道工序;机器11加工阀块6、8、4、5、1的第6道工序;机器12加工阀块2、7、3的第6道工序。 3.4.3完成时间矩阵TC 根据阀块加工顺序规则,结合式(23)所示的加工时间矩阵TP,生成阀块在所选机器上完成相应工序加工的完成时间矩阵TC: (24) 3.5结果对比 将MFPSO算法用于求解该液压阀块加工车间调度问题,并与车间实际调度方案(依据现场实际经验排序)以及PSO算法、MPSO算法[14]、EPSO算法[20]、ACO算法进行对比,以验证所提算法的有效性。 令PSO算法、MPSO算法、EPSO算法的参数设置与MFPSO算法相同:种群规模N=20,函数维数n=8×6=48,最大迭代次数tmax=500,惯性权重wmin=0.4、wmax=0.9,加速常数c1=c2=cj=1.49;令ACO算法的种群规模N=20,信息素挥发系数ρ=0.5,固定概率P0设置为[0,1]之间的随机数。上述5种算法独立运行10次的最优优化结果见图5,所得优化结果的平均值见表4。 图5 5种算法的最优优化结果曲线 表4 优化结果(最大完成时间)对比 min 由图5和表4可知,MFPSO算法所得结果最优,其中,与图5所对应的最优调度方案的甘特图如图6所示。 图6 MFPSO算法最优调度方案的甘特图 由图6可知,MFPSO算法所得的最优调度方案中各机器上的作业量比较均衡,符合实际需求,同时缩短了最大完成时间,故本文所提的MFPSO算法是有效、可行的,采用该调度方案可提高液压阀块加工车间的生产效率,也有助于实现节能减排、节约成本。 (1)为平衡算法的全局和局部搜索能力,提出了多作用力微粒群(MFPSO)算法,采用多作用力阶段性搜索策略,将搜索过程划分为前期、中期、后期3个阶段,并对应构造单一斥力、平衡引斥力、单一引力3种作用力规则,在不同搜索阶段采用不同的作用力规则,丰富了微粒间的作用力,兼顾了对算法种群多样性和收敛速度的要求,提高了算法的搜索机制和寻优性能。 (2)为解决液压阀块加工车间调度问题,考虑工序间和机器间的约束关系,以最大完成时间最小为目标,给出了液压阀块加工车间调度优化模型。利用矩阵变量来处理约束条件,给出了一种基于矩阵的微粒编码、解码方法。将MFPSO算法用于求解液压阀块加工车间调度问题,并与车间实际调度方案以及微粒群(PSO)算法、中值导向微粒群(MPSO)算法、扩展微粒群(EPSO)算法、蚁群(ACO)算法进行了对比,结果表明,本文提出的MFPSO算法结果最优,从而验证了该算法的有效性。 (3)液压技术是衡量机械制造业水平的最重要的基础技术之一,本文从工艺流程控制的角度对其进行了研究,针对液压阀块加工车间调度问题,提出MFPSO算法以寻求最优调度方案,为解决液压阀块加工车间调度问题提供了一条新的途径。MFPSO算法采用前期、中期、后期3个阶段的搜索策略,需要对以下问题进行进一步的研究:搜索阶段的数目划分与动态混合以进一步提高优化性能;不同搜索阶段的高效切换策略以适应在线寻优问题。 [1]Haouari M,Hidri L,Gharbi A.Optimal Scheduling of a Two-stage Hybrid Flow Shop[J].Mathematical Methods of Operations Research,2006,64(1):107-124.[2]黎展滔,陈庆新,毛宁.具有前成组约束的两阶段柔性流水车间的启发式算法[J].机械工程学报,2012,48(22):189-198. Li Zhantao,Chen Qingxin,Mao Ning.Heuristic Algorithms for Two-stage Flexible Flow Shop Scheduling with Head Group Constraint[J].Journal of Mechanical Engineering,2012,48(22):189-198. [3]张国军,李婵娟,朱海平,等.不确定信息条件下Job-shop调度的混合智能算法[J].中国机械工程,2007,18(16):1939-1942. Zhang Guojun,Li Chanjuan,Zhu Haiping,et al.A Hybrid Intelligent Algorithm for Job-shop Scheduling under Uncertain Information Environment[J].China Mechanical Engineering,2007,18(16):1939-1942. [4]张洁, 张朋, 刘国宝. 基于两阶段蚁群算法的带非等效并行机的作业车间调度[J].机械工程学报,2013,49(6):136-144. Zhang Jie, Zhang Peng, Liu Guobao. Two-stage Ant Colony Algorithm Based Job Shop Scheduling with Unrelated Parallel Machines[J].Journal of Mechanical Engineering,2013,49(6):136-144. [5]周辉仁,唐万生,魏颖辉.基于微粒群算法的柔性流水车间调度优化[J].中国机械工程,2010,21(9):1053-1057. Zhou Huiren,Tang Wansheng,Wei Yinghui.PSO-based Optimization of Flexible Flow-shop Scheduling[J].China Mechanical Engineering,2010,21(9):1053-1057. [6]赵诗奎,方水良.基于工序编码和邻域搜索策略的遗传算法优化作业车间调度[J].机械工程学报,2013,49(16):160-169. Zhao Shikui,Fang Shuiliang.Operation-based Encoding and Neighborhood Search Genetic Algorithm for Job Shop Scheduling Optimization[J].Journal of Mechanical Engineering,2013,49(16):160-169. [7]Xu Ye,Wang Ling.Differential Evolution Algorithm for Hybrid Flow-shop Scheduling Problems[J].Journal of Systems Engineering and Electronics,2011,22(5):794-798. [8]Shi Y,Eberhart R C.Fuzzy Adaptive Particle Swarm Optimization[C]//IEEE Congress on Evolutionary Computation, May, 2001.Piscataway, New Jersey, USA: IEEE, 2001:101-106.[9]Bratton D,Kennedy J.Defining a Standard for Particle Swarm Optimization[C]//The 2007 IEEE Swarm Intelligence Symposium(SIS 2007),April 1-5.Honolulu, HI,USA:IEEE,2007:120-127. [10]叶南海,戚一男,陈凯,等.基于改进PSO的可靠性稳健优化计算方法[J].中国机械工程,2012,23(5):551-555. Ye Hainan,Qi Yinan,Chen Kai,et al.A Computational Method on Reliability Robust Optimization Based on Improved PSO[J]. China Mechanical Engineering, 2012, 23(5): 551-555. [11]韩江洪,李正荣,魏振春.一种自适应粒子群优化算法及其仿真研究[J].系统仿真学报,2006,18(10):2969-2971. Han Jianghong,Li Zhengrong,Wei Zhenchun.Adaptive Particle Swarm Optimization Algorithm and Simulation[J].Journal of System Simulation,2006,18(10):2969-2971. [12]Chen W N, Zhang J, Lin Y, et al. Particle Swarm Optimization with an Aging Leader and Challengers[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(2): 241-258.[13]刘朝华, 张英杰, 章兢,等.一种双态免疫微粒群算法[J].控制理论与应用,2011,28(1):65-72. Liu Zhaohua,Zhang Yingjie,Zhang Jing,et al.A Novel Binary-state Immune Particle Swarm Optimization Algorithm[J].Control Theory & Applications,2011,28(1):65-72.[14]Beheshti Z, Shamsuddin S M H, Hasan S. MPSO: Median-oriented Particle Swarm Optimization[J].Applied Mathematics and Computation, 2013, 219(11): 5817-5836.[15]Qu B Y,Suganthan P N,Das S.A Distance-based Locally Informed Particle Swarm Model for Multimodal Optimization[J].IEEE Transactions on Evolutionary Computation,2013,17(3):387-402.[16]Mendes R,Kennedy J,Neves J.The Fully Informed Particle Swarm:Simpler,Maybe Better[J].IEEE Transactions on Evolutionary Computation,2004,8(3):204-210.[17]陈保娣,曾建潮.改进的吸引扩散微粒群算法[J].控制理论与应用,2010,27(4):451-456. Chen Baodi,Zeng Jianchao.Modified Attractive and Repulsive Particle Swarm Optimization[J].Control Theory & Applications,2010,27(4):451-456. [18]韩飞,杨春生,刘清.一种改进的基于梯度搜索的微粒群优化算法[J].南京大学学报(自然科学),2013,49(2):196-201. Han Fei, Yang Chunsheng, Liu Qing. An Improved Particle Swarm Optimization Based on Gradient Search[J].Journal of Nanjing University(Natural Sciences), 2013, 49(2): 196-201. [19]Huang T, Mohan A S. A Microparticle Swarm Optimizer for the Reconstruction of Microwave Images[J].IEEE Transactions on Antennas and Propagation, 2007, 55(3): 568-576.[20]莫思敏, 曾建潮, 谢丽萍. 扩展的微粒群算法[J].控制理论与应用, 2012, 29(6): 811-816. Mo Simin,Zeng Jianchao, Xie Liping. Extended Particle-swarm Optimization Algorithm[J].Control Theory & Applications,2012,29(6):811-816. (编辑苏卫国) A MFPSO Algorithm for Solving Hydraulic Manifold Processing Shop Scheduling Chen Dongning1,2Zhang Ruixing1,2Yao Chengyu3Qian Yanhui1,2 1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science(Yanshan University),Ministry of Education of China,Qinhuangdao,Hebei,066004 3.Key Laboratory of Industrial Computer Control Engineering of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 Considering the constraints between processes and machines,an optimization model with the objective of minimizing the maximum completion time or makespan was put forward to solve manifold processing shop scheduling problem effectively.To balance the ability of global and local search of the algorithm,a MFPSO algorithm was proposed,which used staged search strategy of multi forces.The search process was divided into three stages:earlier-stage,medium-stage and later-stage,and three kinds of force rules,were correspondingly constructed,which were single repulsion force rule,balanced attraction and repulsion force rule and single attraction force rule.Different force rules were adopted in different search stages so as to improve the search mechanism and search performance of the algorithm.The MFPSO algorithm was applied in solving manifold processing shop scheduling problem. A particle encoding and decoding method was presented based on matrix, which made use of matrix variables to deal with the constraints of the problem. Finally, the MFPSO algorithm presented herein shows better performance compared with PSO algorithm,median-oriented PSO algorithm,extended PSO algorithm and ant colony optimization algorithm in optimizing manifold processing shop scheduling problem,thus its effectiveness was verified. manifold processing shop scheduling;particle swarm optimization(PSO) algorithm;force rule;multi force PSO(MFPSO) algorithm 2014-08-29 国家自然科学基金资助项目(51405426);河北省自然科学基金资助项目(E2012203015);河北省教育厅资助科研项目(ZH2012062) TP18;TH173DOI:10.3969/j.issn.1004-132X.2015.03.015 陈东宁,女,1978年生。燕山大学机械工程学院副教授、博士。主要研究方向为系统可靠性及智能优化。获国家科技进步二等奖1项。出版专著2部,发表论文38篇。张瑞星,女,1987年生。燕山大学机械工程学院硕士研究生。姚成玉,男,1975年生。燕山大学电气工程学院教授、博士。茜彦辉,男,1988年生。燕山大学机械工程学院硕士研究生。
3 液压阀块加工车间调度MFPSO优化
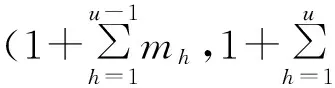


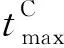
4 结语
