谱载荷下加载次序效应定量评价的初步研究

储　军　郑松林

1.上海理工大学，上海， 200093　　2.温州大学，温州， 325035

谱载荷下加载次序效应定量评价的初步研究

储军1,2郑松林1

1.上海理工大学，上海， 2000932.温州大学，温州， 325035

通过对40Cr材料光滑试样进行不同加载次序的三级程序载荷疲劳试验，验证并分析了载荷作用次序对疲劳强度累积强化效果的影响。试验结果表明：按照载荷从小到大逐渐增加的次序加载时，锻炼载荷对疲劳强度的累积强化效果最大，并且与三级锻炼载荷分别独立作用时强化效果的叠加值接近；而在其他加载次序下，累积强化效果分别受到不同程度的影响。最后，通过对疲劳试验数据的统计分析，初步研究了谱载荷下加载次序对总体累积强化效果的修正系数，并对之前建立的随机载荷下累积强化效果模型做出了修正，为建立考虑低载强化效应的疲劳累积理论进行了探索。

疲劳累积理论；载荷作用次序；强化效果；载荷强化

0　引言

低于疲劳极限的应力循环对结构疲劳强度的强化效应是疲劳领域中较为独特的现象，国外学者将这一现象称为“coaxing”效应。从英国人Gough在低碳钢试样的弯扭复合疲劳试验中发现这一现象开始[1]，欧美、日本和国内众多学者，针对不同的材料、热处理工艺以及环境因素对低载强化效应做了大量的研究[2-5]。

汽车结构件在车辆运行过程中受到的随机载荷，大部分是幅值低于疲劳极限的低幅载荷，在结构强度失效前，这些大量的低幅载荷有可能对结构造成低载强化。试验研究表明，汽车变速器齿轮、后桥、半轴等结构件在经受国家标准规定的试验载荷后，结构强度都得到了不同程度的提高[6-7]。

在现有的疲劳累积理论中，Miner线性理论最简单易行，应用也最广泛，但没有考虑到各级载荷间的相互影响，也没有考虑低于疲劳极限的应力的锻炼效应；而其他的一些疲劳累积理论都有较大的局限性，只能在一些特定的条件下使用。因此，对于疲劳累积理论的研究，仍有进一步探索的空间。

之前的研究，通过对光滑试样分别改变载荷幅值大小和载荷作用次数的疲劳试验，验证并分析了汽车传动轴40Cr材料的低载强化特性，并初步推导出载荷谱作用下的累积强化效果模型[8]，但这一强化效果模型是基于恒幅锻炼载荷的试验结果分析推导出来的，并没有考虑不同载荷先后顺序对低载强化效果的影响。然而很多的试验结果表明，相同的载荷大小及载荷作用次数下，采用高→低次序载荷造成的疲劳累积损伤往往比采用低→高次序载荷造成的疲劳累积损伤严重，说明即使在两级载荷作用下，载荷先后顺序对结构的疲劳强度也存在影响[9]。要想让低载强化的效果较好地反映结构件的真实受载情况，建立更为合理的疲劳累积效果模型，必须考虑低幅载荷的加载次序对累积强化效果的影响。

1　不同载荷作用次序下的疲劳试验

经过前期的扭转疲劳试验，推算得到40Cr光滑圆试样的疲劳极限τ-1为220.9 MPa，详细的疲劳试验结果见文献[10]；其中载荷Tmax=301 N·m(应力比r=0.1)时，试样的平均疲劳寿命约为219 280次载荷循环，该值作为后文加速寿命试验的比较依据。以上述疲劳极限的60%、70%、80%为应力水平，对试样施加三级程序载荷进行疲劳试验，分析不同应力水平下载荷的先后顺序对强化效果的影响。试验拟定以最小载荷5500次、中等载荷3500次、大载荷1000次为一个循环块，其中各载荷循环的应力比r均等于0.1，最大值分别为最小载荷Tmax1=88 N·m、中等载荷Tmax2=99 N·m、大载荷Tmax3=111 N·m，以小中大、大小中、中大小轮换的载荷次序分别累积加载锻炼150 000次后，进行疲劳强度验证试验，对各个锻炼后的试样在r=0.1、Tmax=301 N·m的循环载荷下进行加速寿命试验，程序加载方式如图1所示，每种载荷次序下取3～4个试样进行试验。图1中①、②、③分别表示Tmax15500次、Tmax23500次、Tmax31000次。

不同载荷作用次序下试样的加速寿命试验结果如表1所示，其中试样P46的加速疲劳试验进行到150万次载荷循环，仍然没有出现疲劳破坏，该试样的试验终止。试样P49、P52经过由低到高的递增载荷作用后，疲劳寿命也明显升高，这都预示着递增载荷会使试样的疲劳强度逐渐得到锻炼提高。

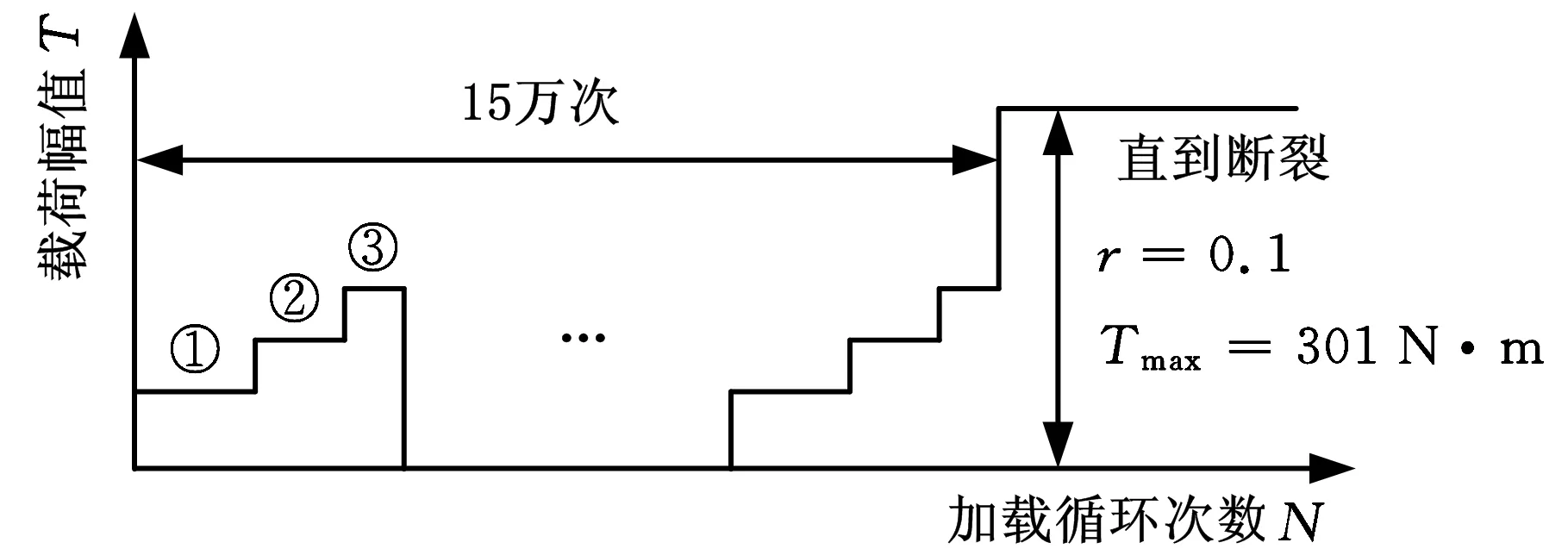
(a)小中大的载荷次序

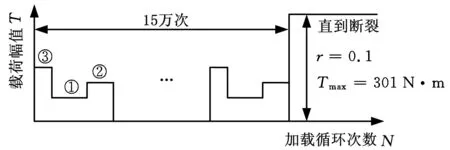
(b)大小中的载荷次序

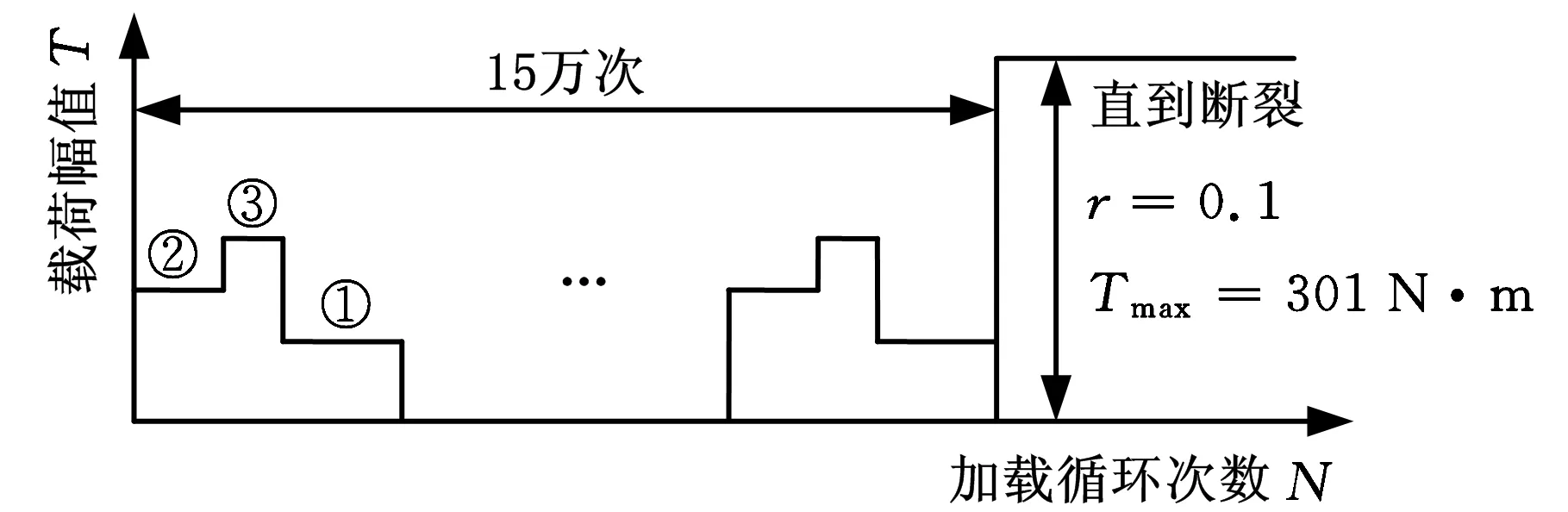
(c)中大小的载荷次序图1　三级程序锻炼载荷的加载方式

由于在小中大的加载次序下出现了试样经大量低幅载荷锻炼后在后续疲劳加速试验中未断裂的情况，需要首先对上述原始数据采用无替换定时截尾的可靠性数据分析方法进行处理[11]，以保证试验数据的有效性和数据处理的可信度。假设在该载荷作用次序下所有试样的总试验时间为tall，在t0时间之前发生了r个断裂失效，第i次断裂失效发生的时间是ti，则试样的平均寿命在置信概率P下的单侧置信下限为θL。代入相应的试验数据，可得

55.63+67.31+150=272.94(万次)

(1)

(2)

其中，n为小中大的加载次序下试验的总样本数，t0为截尾寿命。从式(2)的结果推断，在按照小中大载荷的加载次序进行了15万次锻炼循环后，试样的平均验证寿命在95%的置信水平下应不低于43.35万次。

小中大、大小中和中大小三组载荷锻炼后的平均验证寿命分别为43.35万次、32.45万次和37.74万次，与试样未经过低幅载荷锻炼的平均寿命21.93万次相比，各增加了21.42万次、10.52万次和15.81万次，说明不同的载荷作用次序对试样的疲劳寿命影响较大。

根据损伤度的定义，以强度值作为损伤变量的计算对象，将上述的寿命验证试验中的疲劳强度与初始疲劳强度的差值，即强度增量，定义为强化变量，也列于表1中。

2　试验结果的分析与评价

假设不考虑三级载荷之间的相互影响，分别以上述各级锻炼载荷独立作用，然后再在相同条件下加载至断裂。独立锻炼载荷的加载方式如图2所示，各级载荷总体锻炼次数下的独立强度增量如表2所示。

图2　独立锻炼载荷的加载方式

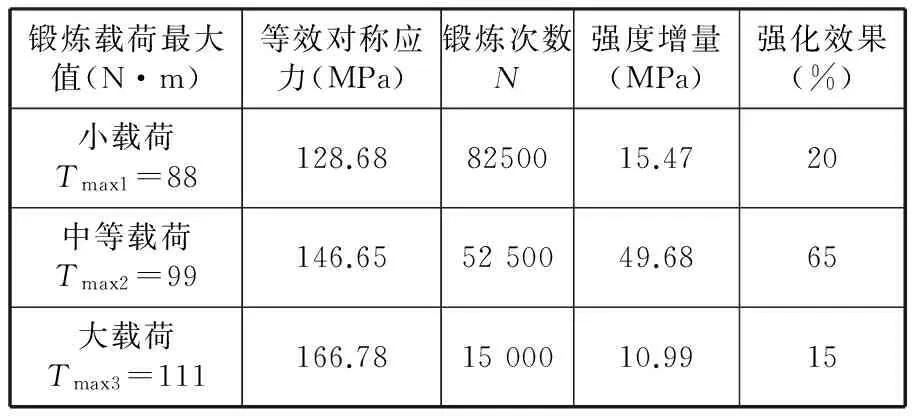
锻炼载荷最大值(N·m)等效对称应力(MPa)锻炼次数N强度增量(MPa)强化效果(%)小载荷Tmax1=88128.688250015.4720中等载荷Tmax2=99146.655250049.6865大载荷Tmax3=111166.781500010.9915

三级载荷在对应的锻炼次数下强度增量的总和为76.14 MPa，这与载荷按照小中大次序加载时的累积强化效果77.03 MPa比较接近，说明载荷按照小中大次序加载时，各级载荷均产生了相应的锻炼作用；载荷按照大小中，或者中大小的次序加载时，累积强化效果都要比各级载荷强化效果的总叠加值要低。其中按照大小中的加载次序是试验累积强化效果最差的情况，由于大载荷最先作用，中小载荷的强化效果都出现了明显下降。

假设当载荷由低到高逐级增大加载时，载荷次序对累积强化效应的影响系数为α；如果大载荷后紧跟着出现的是低一级的中等载荷，或者中等载荷后紧跟着出现的是比其低一级的小载荷，由于后面施加的载荷强化作用比其独立加载时强化效果要低，假设此时的载荷次序效应系数为β(β<1)；而如果大载荷后紧邻出现的是跨越两级的小载荷作用，设此时的载荷次序效应系数为γ(γ<1)。当后面施加的载荷对结构强度呈现出损伤作用时，载荷次序效应系数小于0。根据上述的假定，三级载荷作用时可能的加载次序及其对累积强化效应的影响系数如表3所示。

表3　加载次序对累积强化效应的影响系数

在随机载荷谱中，将低于疲劳极限的所有载荷划分成三级，假设小中大各级载荷在其区间内累积频次下独立作用时的强化效果分别为x、y、z，按照数学排列大中小三级载荷可能出现以下6种组合情况：①小中大作用次序下的累积强化效果，x+α y+α z；②小大中作用次序下的累积强化效果，x+α z+β y；③中小大作用次序下的累积强化效果，y+β x+α z；④中大小作用次序下的累积强化效果，y+α z+γ x；⑤大小中作用次序下的累积强化效果，z+γ x+α y；⑥大中小作用次序下的累积强化效果，z+β y+β x。

假设在随机载荷谱中每种情况出现的概率是相同的，则载荷作用次序对总体的累积强化效果修正系数η应为6种情况的均值:

(3)

根据表1的试验结果和上述的假设条件，列出载荷作用次序对传动轴试样累积强化效果的影响系数方程：

(4)

求得α=1.01，β=0.64，γ=-0.1。

从表1的试验数据也可以看出，当大载荷先作用时，试样的平均验证寿命明显下降，说明紧跟其后的中、小载荷强化效果降低，小载荷甚至不产生强化效应。在中大小的载荷作用次序下，如果忽略小载荷的强化效应，中等载荷和大载荷两级锻炼载荷强化效果的叠加值60.67 MPa与试验累积强化效果59.31 MPa也比较接近。说明当大载荷后紧邻出现的是跨越两级的小载荷，则小载荷的强化作用几乎可忽略不计，即载荷次序效应系数γ约为0。在大小中的载荷作用次序下，假定完全忽略小载荷的强化效应，中等载荷此时的强化效应只有其单独作用时的61%。

3　谱载荷下加载次序效应定量评价的初步研究

由于试验数据的分散性和随机性，试验本身也存在误差，为便于后续的分析和计算，近似地将上述载荷次序效应系数简化处理。以从小到大的加载次序产生的累积强化效果为基准，同时忽略后加载的跨越两级小载荷强化作用，将其他载荷作用次序对累积强化效应的影响做归一化处理。即令α=1，γ=0，则β≈0.61，推算出大中小三级载荷可能出现的6种情况累积强化效果系数列于表4。

表4　三级载荷不同作用次序下的累积强化效果系数

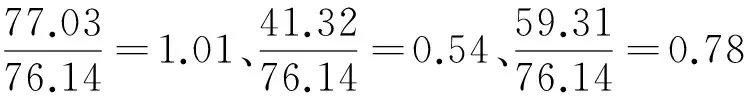
对于随机载荷谱，由于载荷谱中的载荷大小、载荷作用次数和载荷作用次序等参数随机性较大，不可能直接按照载荷谱的时间历程进行累积强化和损伤分析，而必须通过概率统计的方法，对载荷谱的特征参数进行统计处理。在确定了载荷谱的特征参数和结构材料的情况下，载荷作用次序对总体的累积强化效果修正系数η可以简化为常量，对文献[8]中谱载荷作用下结构疲劳累积损伤与强化效果的耦合模型修正为

W=∫LI(τ,lgN,S)ds=η∫LI(τ,lgN)ds=

(5)

式中，S代表载荷的作用次序；I(τ，lgN)为在应力水平τ下循环锻炼N次的强化效果；f(τ)为随机载荷下应力水平τ的概率密度函数；L为疲劳累积效果的积分路径，它代表了载荷谱中各级应力下强化或损伤变量的轨迹。

在随机载荷谱中，载荷作用次序修正系数η主要由材料的低载强化特性、载荷的分布以及载荷的级数划分等因素决定。需要说明的是，本文试验中仅将载荷分成三级，而在真实的随机载荷下，载荷是随意变化的，用来进行随机载荷谱累积频次统计的循环计数法，通常将载荷分成8级，那将使试验的时间和试样数量成几何级的增长，但对进一步反映加载次序的影响和精确推算的总体累积强化效果意义不大。

4　结论

(1)通过对40Cr材料光滑试样不同加载次序的三级程序载荷疲劳试验，验证并分析了载荷作用次序对累积强化效果的影响。试验结果表明：载荷按照从小到大逐渐增加的次序加载时，各级载荷均产生了相应的锻炼作用，此时的累积强化效果最大；载荷按照从大到小，或者先中等，再大小的次序加载时，累积强化效果都要比各级载荷强化效果的总叠加值要低。

(2)在不同幅值的低幅载荷对结构连续进行锻炼作用时，前期作用的小幅值载荷对后期的大幅值载荷强化效果基本不产生影响；而如果前期作用的是大幅值载荷，将会削弱后期的中小幅值载荷的强化效应。根据试验结果预测，其中中等幅值载荷的强化效果约降低为原先的60%，而小幅值载荷的强化效应几乎为0。

(3)根据三级程序载荷不同加载次序对总体累积强化效果影响的统计分析，对之前建立的随机载荷下累积强化效果模型做了进一步的修正，完善了低载强化效应的三个主要影响因素，即载荷的作用频次、幅值大小及作用次序，为建立考虑低载强化效应的疲劳累积理论进行了更深入探讨。

[1]Sinclair G M.An Investigation of the Coaxing Effect in Fatigue of Metals[R]. Urbana:Illinois University,1952.

[2]Nicholas T. Step Loading for Very Cycle Fatigue[J]. Fatigue Fracture of Engineering Materials Structures, 2002,25:861-869.

[3]Nakajima M, Jung J W, Uematsu Y, et al. Coaxing Effect in Stainless Steels and High-strength Steels[J]. Key Engineering Materials, 2007, 346: 236-238.

[4]Nakajima M, Akita M, Uematsu Y. Effect of Strain-induced Martensitic Transformation on Fatigue Behavior of Type 304 Stainless Steel[J]. Procedia Engineering, 2010,2:323-330.[5]李岩，鲍蕊，费斌军,等. 随机谱中小幅载荷对裂纹扩展寿命的影响[J]. 飞机设计, 2008(3):8-12.

Li Yan, Bao Rui, Fei Binjun,et al. The Influence of Low Amplitude Cycles in Random Spectra on Crack Growth Life[J]. Aircraft Design, 2008(3):8-12.

[6]郑松林. 低幅载荷对前轴疲劳寿命影响的试验研究[J]. 机械强度, 2002,24(4): 547-549.

Zheng Songlin. Studying The Effectof Low Amplitude Loading on Fatigue Life of Truck Front Axle[J]. Journal of Mechanical Strength, 2002,24(4): 547-549.

[7]卢曦，郑松林，寇宏滨,等. 圆柱齿轮低载强化试验研究[J]. 中国机械工程, 2005, 16(23): 2109-2111.

Lu Xi,Zheng Songlin,Kou Hongbin,et al. Experimental Study on Strengthening under Low Amplitude Loading for Cylindrical Gears[J]. China Mechanical Engineering, 2005, 16(23): 2109-2111.

[8]储军，郑松林，冯金枝,等. 基于低幅锻炼载荷的累积强化效果模型[J].机械工程学报,2011, 47(16):30-34.

Chu Jun, Zheng Songlin, Feng Jinzhi, et al. A Fatigue Cumulative Strengthen Effect Model Based on the Low-amplitude Training Load[J].Chinese Journal of Mechanical Engineering, 2011, 47(16):30-34.

[9]王旭亮，聂宏. 考虑载荷加载顺序的模糊Miner理论研究[J].中国机械工程,2008,19(22)：2725-2728.

Wang Xuliang, Nie Hong. Study on Fuzzy Miner’s Rule Considering Load Sequence[J].China Mechanical Engineering,2008,19(22)：2725-2728.

[10]Chu Jun, Zheng Songlin, Feng Jinzhi. A Model of Cumulative Fatigue Strengthening Effect Due to Coaxing[J]. Fatigue & Fracture of Engineering Materials & Structures, 2012,35(5):433-440.

[11]胡俏，徐灏，谢里阳. 疲劳应力统计分布与可靠度计算模型[J].机械工程学报, 1994, 30(2):105-110.

Hu Qiao, Xu Hao, Xie Liyang.Fatigue Stress Distribut10n and Reliability Calculation Model[J]. Chinese Journal of Mechanical Engineering,1994, 30(2):105-110.

(编辑郭伟)

Preliminary Study of Quantitative Evaluation for Spectrum Load Sequence Effect

Chu Jun1,2Zheng Songlin1

1.University of Shanghai for Science and Technology,Shanghai,200093 2.Wenzhou University,Wenzhou,Zhejiang,325035

According to the three level program load fatigue test on the 40Cr material smooth specimens with different loading sequences, the influences of load sequence on cumulative fatigue strengthening effect were verified and analyzed. The test results show that, in accordance with the sequence from small to large loads, the exercise loads caused the maximum cumulative fatigue strengthening effect, which approached to the added value of three exercise load’s strengthening effects independently. Whereas in other load sequences, the cumulative strengthening effect were decreased in different degrees. Finally, based on the statistical analysis of fatigue test data, a correction factor η was proposed, which expressed the influences of spectrum load sequence on overall cumulative strengthening effect. Moreover, the previous fatigue cumulative strengthening effect model under the random load was modified, which made a deep study of fatigue cumulative theory considering load strengthening effect.

fatigue cumulative theory; load sequence; strengthening effect; load strengthening

2013-11-12

国家自然科学基金资助项目(50875173)；浙江省自然科学基金资助项目(Y1100007)；上海市科委基础重点基金资助项目(13JC1408500)

TH114< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.03.014

储军，男，1980年生。上海理工大学机械工程学院博士研究生，温州大学机电工程学院讲师。主要研究方向为车辆结构强度理论及轻量化设计。郑松林，男，1958年生。上海理工大学机械工程学院教授、博士研究生导师。