一种关节型串联机器人工作空间边界提取的新方法

侯雨雷　王嫦美　胡鑫喆　曾达幸　赵永生

1.燕山大学，秦皇岛，0660042.东方电气集团东方电机有限公司，德阳，618000

一种关节型串联机器人工作空间边界提取的新方法

侯雨雷1王嫦美2胡鑫喆1曾达幸1赵永生1

1.燕山大学，秦皇岛，0660042.东方电气集团东方电机有限公司，德阳，618000

利用杆件极限组合原理，结合定步距角法可固定关节变量的特点，提出一种提取工作空间边界的新方法——“极限定步距角法”，阐明思路并给出其具体实施步骤。以某型ABB机器人为例，利用D-H法设定机器人连杆参数及关节变量，并建立机器人坐标系与D-H坐标系间的转换关系，获得机器人边界关键点位置，进而借助MATLAB软件绘制机器人手腕处三维透视工作空间，对比分析表明所获边界关键点精度完全满足商用机器人标准。所提出的方法简单有效、计算便捷、利于操作，对串联机器人工作空间的研究具有理论指导意义和实践应用价值。

串联机器人；工作空间；边界；极限定步距角

0　引言

机器人工作空间的大小代表其活动范围，是衡量机器人工作能力的一个重要运动学指标[1]。关节型串联机器人具有高度的能动性及广阔的可达空间，精确地获取其工作空间边界有利于机器人合理设计、选型及与周边设备有效配合。

目前，求取串联机器人工作空间的方法主要分为解析法、图解法和数值法。其中，解析法需建立复杂的数学方程，难以满足工程应用要求[2]；商用工业机器人多采用图解法来直观地呈现二维空间，但该方法不适合准确描述三维图形[3]；数值法是将关节组合变量作为输入，而以对应的位置解集作为输出[4]，因此工作空间体现为点状云图。随着计算机运算能力的提升，数值法愈加体现出其编程思路简单、图形处理能力强的优势[5]。

数值打点法成像最具代表性的实现方法有Rastegar等[6]引进的基于随机抽样组合原理的蒙特卡洛法、钟勇等[7]对前者改进后的定步距角法、赵燕江等[8]提出的基于结构建模的MATLAB/Simulink仿真法等。刘晓宇等[9]对比了上述3种主要方法，认为蒙特卡洛法与定步距角法更适用于串联机器人工作空间的求解，其中后者利用机器人运动学正解打出定步长的工作空间点，能以相同的成像点数绘制出更为清晰完整的边界，还能通过固定某些关节来查看机器人在特定位姿下的工作空间。

由于点状云图无法确切地表现内外边界，因此许多学者进行了云图边界点的降维提取与三维空间曲面的再现研究工作，一般主要筛选利用蒙特卡洛法生成的空间云图，其中包括Dabid等[10]的栅格搜索法、曹毅等[11]的极值搜索法、印峰等[12]的文本搜索法及赵杰等[13]的逆解搜索法等，上述各方法理论体系较为完备，然而其所基于的蒙特卡洛云图是工作空间的近似描述，即便工作量巨大，得到的也只能是逼近边界。Brezovnik等[14]、Gianni等[15]另辟蹊径，分别基于准三维模型法与计算机像素法再现了较为美观的三维工作空间边界，但这两种方法的可操作程度尚不够完善；杨文珍等[16]基于CAD软件建立了灵巧手运动学仿真的工作空间三维模型，由于其不涉及运动学正问题，且二维结构建模简单、三维实体生成速度快，若能成功解决三维曲面间的交叉问题，将有望成为一种通用性强的工作空间边界提取办法。

本文在广泛调研现有工作空间边界提取方法的优势和不足基础上，利用定步距角法可固定关节的特点，根据杆件极限组合原理直接获得串联机器人的二维、三维空间边界，进而形成一种新的串联机器人工作空间提取方法，即“极限定步距角法”。

1　“极限定步距角法”思路与步骤

本文针对应用较为广泛的关节型串联机器人，利用定步距角法能固定某些关节的特色之处，提出一种可以直接提取其工作空间边界的新方法——“极限定步距角法”，其核心思想为：由于关节型串联机器人末端参考点的位置主要由机器人的杆长和转角范围决定[14]，因此将机器人关节角的极限情况进行组合，通过定步长打点方式直接绘制二维工作空间边界曲线，在对之进行精确裁剪和关键点的验证后，最终分区拟合出机器人工作空间三维边界曲面。

“极限定步距角法”提取关节型串联机器人腕部参考点的工作空间边界的流程参见图1。

图1　“极限定步距角法”提取串联机器人工作空间边界流程图

“极限定步距角法”提取关节型串联机器人腕部工作空间边界的具体实施步骤如下：

(1)关节型串联机器人的前三个转动关节θ1、θ2、θ3(分别存在于基座与腰部、腰部与大臂、大臂和小臂之间)决定着机器人末端腕部参考点的活动范围，建立机器人的基坐标系O0X0Y0Z0，并依次在其第1～4个转动关节处分别建立Xi、Yi、Zi(i=1，2，3，4)轴，其中Zi轴是关节的转轴，若相邻的Zi-1、Zi轴不相交，则Xi轴是二者公垂线；连杆参数a为Zi-1沿Xi-1至Zi的距离，αi-1为Zi-1绕Xi-1转至Zi的角度，di为Xi-1沿Zi至Xi的距离，θi为Xi-1绕Zi转至Xi的角度，依此法则建立D-H连杆坐标系[17]，如图2所示。

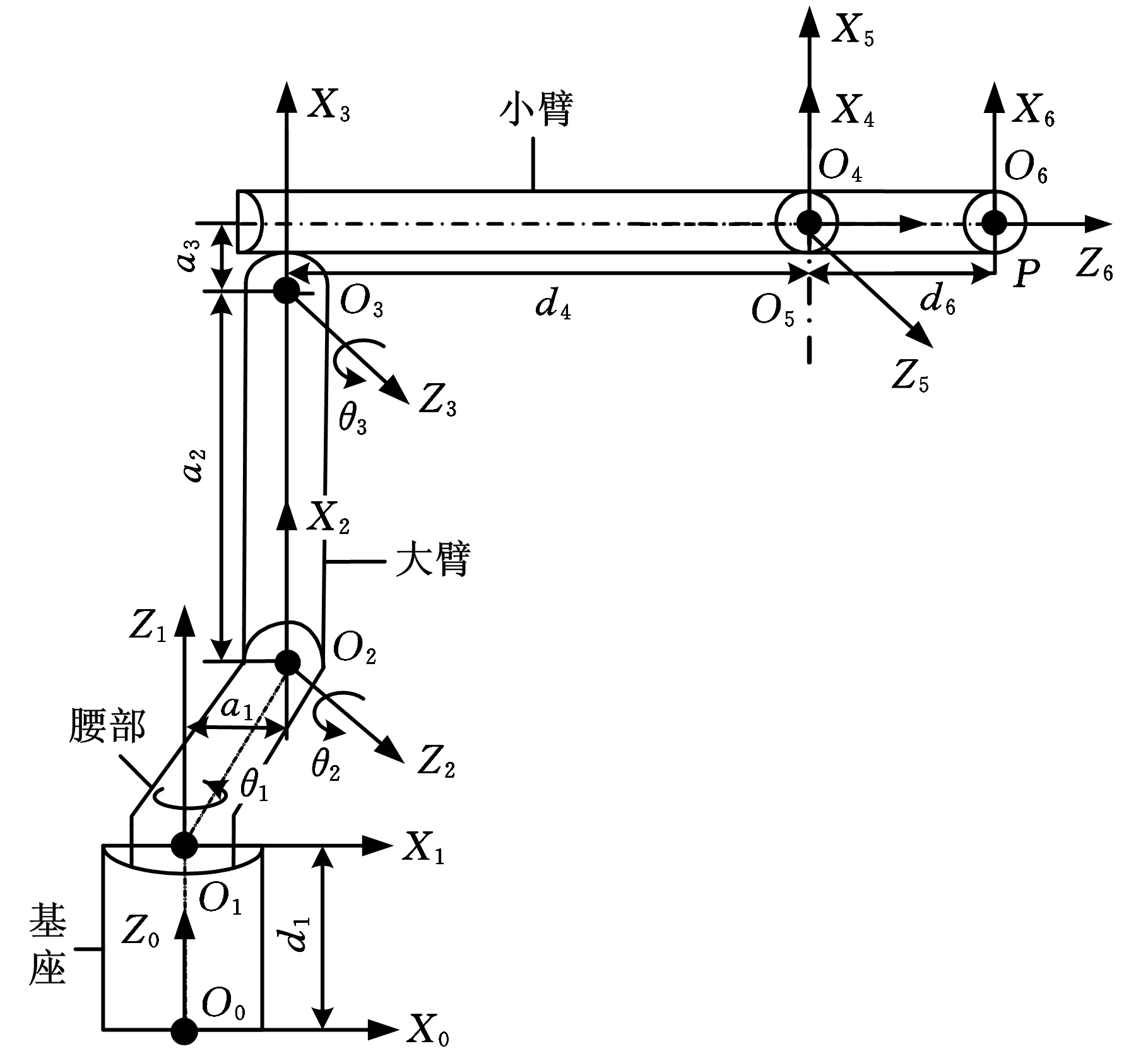
图2　关节型串联机器人D-H连杆坐标系

分析连杆坐标系及杆件参数，设点P为机器人末端的腕部中心参考点，其位置正解方程如下：

(1)

(2)利用机器人原始变量参数直接生成D-H坐标系下的工作空间，根据云图轮廓尺寸检验与参考空间是否一致，若一致则直接进入提取二维“完整边界”步骤；若不一致则需寻求机器人原始坐标系的建立法则，进而重新确认机器人关节变量范围的极限值。设机器人前三个关节在D-H坐标系下的参数范围分别为(θ1min,θ1max)、(θ2min,θ2max)、(θ3min,θ3max)，将第二、三关节变量参数的极限情况进行组合，即固定机器人第一关节角(一般设为0°)，另一关节角任设一个极限角度，再一关节角在其转动范围内从关节1到关节i定步长取值，分段绘制机器人二维空间“完整边界”。

机器人的二维“完整边界”即为机器人腕部所能到达的所有极限位置，通常内部存在线条交叉。以机器人的第二、三个关节转动中心点O2、O3以及小臂末端的参考点O4(图2)可否连成一条直线为界，“完整边界”的生成情况分为两类：第一类是O2、O3及O4三点未能连成一条直线，即当|θ3|<90°-arctan(a3/d4)时，边界由四条曲线L1、L2、L3与L4头尾相接而成(图3)，对应关节变量的极限组合情况分别为：θ2=θ2min与θ3=(θ3min,θ3max)，θ2=(θ2min,θ2max)与θ3=θ3max，θ2=θ2max与θ3=(θ3max,θ3min)，θ2=(θ2max,θ2min)与θ3=θ3min；第二类是当|θ3|≥90°-arctan(a3/d4)时，则在第一边界类型的基础上增设一条O2、O3及O4连成一条直线时的最高边界L5(图4)，对应的变量极限组合为θ2=(θ2min,θ2max)与θ3=90°-arctan(a3/d4)。

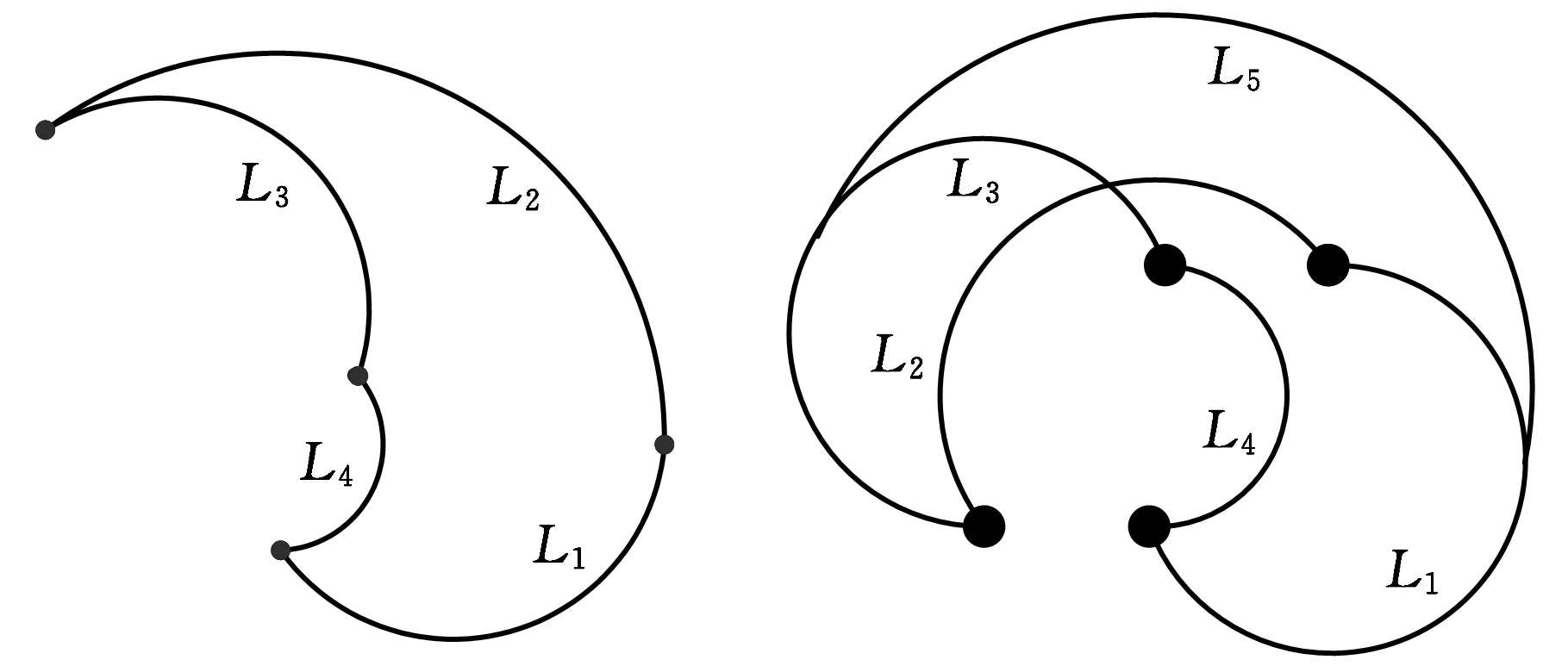
图3　机器人第一类工作空间边界图4　机器人第二类工作空间边界

(3)剔除机器人二维“完整边界”内部可能产生的交叉曲线，形成首尾顺序相接的“单向边界”并检验边界关键点。

本文提出一种较为简便的“数值逼近法”来剔除虚假边界：由于两相交边界曲线所对应数学方程即为运动学位置正解方程，因此只需若干次调整相应的极限变量输入，便能得到最为接近的相交点(关键点)坐标，且关键点的精度可高达到0.1 μm；该方法突破了另行拟合两相交边界曲线方程的常规思路，能够很好地实现机器人工作空间关键点的准确获取。

参照现今商用机器人标准，若所获关键点坐标与标准参考值的偏差在±0.5 mm以内，则边界验证通过；否则必须重新生成边界，再次检验；若依然不符则需通过三维建模软件或者机器人专用软件来共同证明之。

(4)在三维边界成形时，若机器人第一关节角范围超过180°，“单向边界”旋转时通常会产生曲面交叉，因此需进一步提取“准三维边界”。

“准三维边界”即为三维工作空间最终成形之前的二维最小内边界与最大外边界。对于第一关节角范围不超过180°的机器人，其“单向边界”即为“准三维边界”；若超过180°，本文提出“双向边界交叉法”来提取之：将第一关节角相差180°的两个“单向边界”叠放于同一坐标系下，在交叉处对之进行精确裁剪，余下的最外层和最内层曲线即为“准三维边界”。该方法使机器人空间边界提取过程中易于忽视且难于处理的三维曲面交叉问题变得简洁明了。

(5)按一定的嵌套规律存储“准三维边界”上的点，并分区域拟合光滑的内边界曲面以及透明的外边界曲面，从而构造出机器人三维工作空间透视图。

2　“极限定步距角法”应用实例

图5所示为ABB IRB 1410机器人(以下简称ABB机器人)，该机器人坚固可靠、活动范围大，是一款工业上常用于焊接、搬运的六自由度关节型串联机器人。鉴于其商用说明书中提供了详细的二维工作空间相关数据，因此通过“极限定步距角法”来提取其工作空间具有可靠的参照性。

(1)依照前文的具体实施步骤对ABB机器人进行D-H建模分析，得到连杆参数与关节角变量范围如表1所示。

表1　ABB IRB 1410机器人连杆参数

由于利用表1中的ABB机器人关节角范围直接求取的工作空间云图与其参考空间不符，因此需重新确认机器人的关节变量范围：通过ABB坐标系向D-H坐标系的转变关系(图6)可知，ABB坐标系是以机器人各轴均处于零点位姿为基准而建立的，且以顺时针旋向为正方向，从而得到D-H坐标系下的机器人第二、三关节角极限值，它们分别为：θ2min=+20°，θ2max=+160°；θ3min=-65°，θ3max=+70°。

(a)ABB坐标系下关节2转角范围(b)D-H坐标系下关节2转角范围

(c)ABB坐标系下关节3转角范围(d)D-H坐标系下关节3转角范围图6　ABB机器人第二、三关节角坐标系转换

(2)由于ABB机器人的第三关节角|θ3|<90°-arctan(a3/d4)，可知其“完整边界”由4条曲线L1、L2、L3与L4首尾相接而成，对应关节变量的极限情况组合分别为：θ2=+20°与θ3=(-65°,+70°)，θ2=(+20°,+160°)与θ3=+70°，θ2=+160°与θ3=(+70°,-65°)，θ2=(+160°,+20°)与θ3=-65°，如图7所示，因其内部无交叉曲线，即为“单向边界”。利用MATLAB软件编程，在普通计算机(CPU：2.8 GHz；内存：2.0 GB)上计算，“单向边界”生成所需最长计算时间为1.362 s。

图7　ABB机器人二维工作空间边界

(3)参照ABB机器人商用工作空间图形及边界关键点位置(图8，表2)，利用“数值逼近法”获取边界各关键点P0～P7的坐标，精确到小数点后1位，如表3所示。可见，圆整后的关键点位置参数与ABB公司提供的数据完全相同，且其对应的关节角参数符合坐标系转换规律，因而验证了所提取二维“单向边界”的正确性。

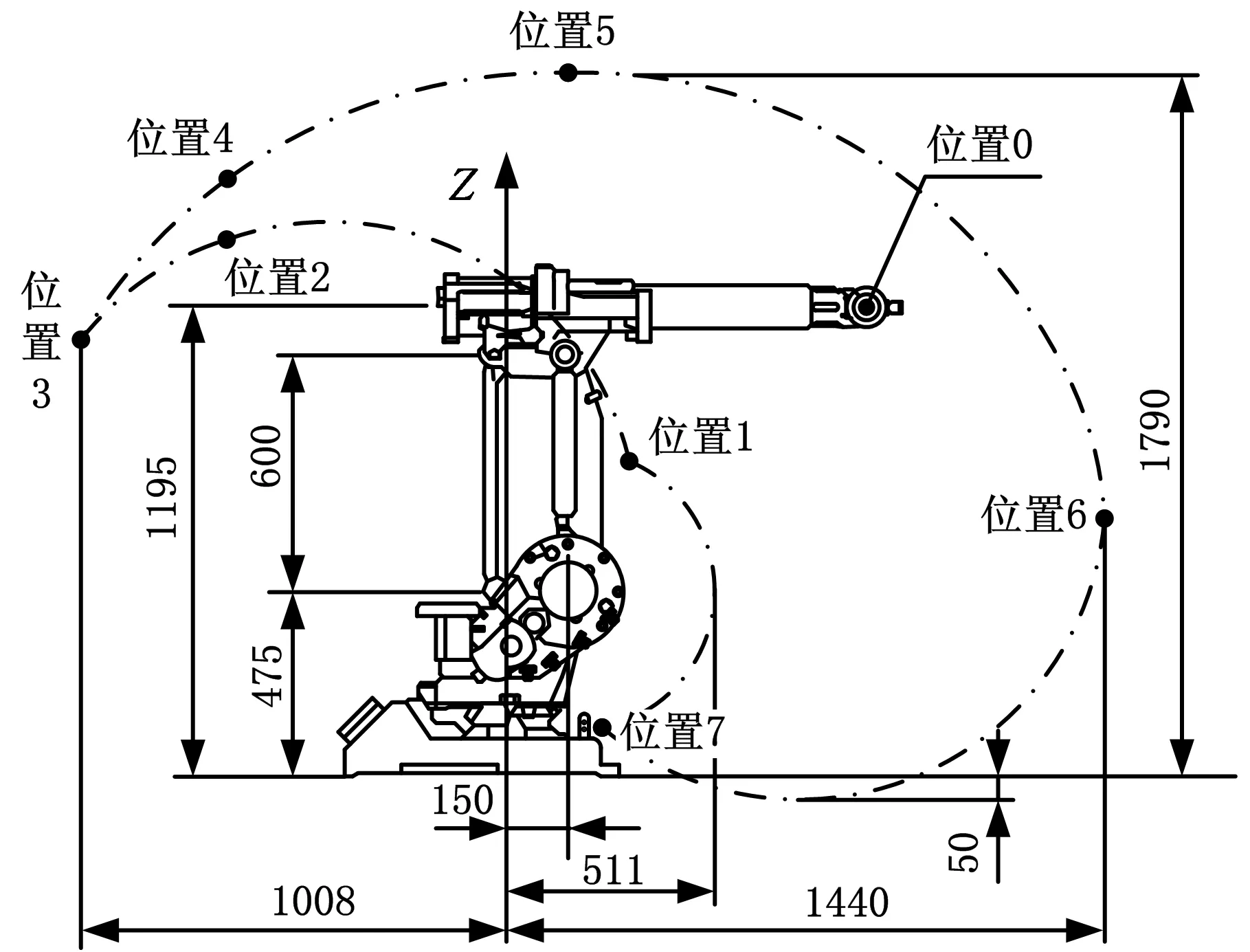
图8　ABB机器人商用二维工作空间边界

位置编号X(mm)Z(mm)θ2(°)θ3(°)08707795001306800-70+702-7161345-70-353-10081104-70-654-5961561-43-6552081792-6-6561142737+70-657239125+70+70

表3　ABB机器人连杆参数

(4)由于ABB机器人第一关节角-170°≤θ≤170°，超出了180°的旋转范围，因此为预防边界曲面交叉，需提取“准三维边界”。在θ1=(-10°,+10°)范围内，机器人的“单向边界”即为“准三维边界Ⅰ”(图7)；在θ1=(-170°,-10°)及θ1=(10°,170°)范围内，利用“双向边界交叉法”分别取θ1相差180°的两个“单向边界”叠放于同一坐标系下(图9)，继而采用“数值逼近法”裁剪虚假边界，从而得到“准三维边界Ⅱ”(图10)。

图9　ABB机器人双向边界交叉

图10　ABB机器人的“准三维边界Ⅱ”

(5)分别将“准三维边界Ⅰ”在θ1=(-10°,10°)区域内、“准三维边界Ⅱ”在θ1=(-170°,-10°)或θ1=(10°,170°)区域内拟合三维工作空间曲面，利用“mesh”命令生成透明的网格状外边界，由“surf”命令生成光滑内边界，渲染后的ABB机器人手腕处的三维空间透视效果如图11所示，所有极限位置一目了然，利用普通个人计算机实现三维造型所需最长计算时间为2.534 s。

图11　ABB机器人三维工作空间透视图

3　结语

针对关节型串联机器人工作空间求解问题，本文提出了能简便、有效提取机器人空间边界的“极限定步距角法”，给出了其前三个关节工作空间边界的获取方案，ABB工业机器人手腕处三维透视工作空间的生成实例充分体现出该方法直截、精准、省时的特征，为关节型串联机器人的轨迹规划和运动干涉的研究提供了便利条件。

“极限定步距角法”较好地解决了关节型串联机器人腕部二维工作空间边界的精确提取、关键点的有效验证以及三维工作空间边界的无交叉拟合问题，为三杆以上关节型串联机器人空间边界的获取奠定了理论基础，也为其他类型串联机器人工作空间的求取与优化提供了应用借鉴。

[1]理查德·摩雷，李泽湘，夏恩卡·萨思特里，等.机器人操作的数学导论[M].北京：机械工业出版社，1998.[2]Wang Y F, Chirikjian, Gregory S. A Diffusion-based Algorithm for Workspace Generation of Highly Articulated Manipulators[C]//Proceedings-IEEE International Conference on Robotics and Automation.Washington DC:IEEE, 2002: 1525-1530.

[3]刘淑春,许纪倩. 工业机器人工作空间及灵活性[J]. 北京科技大学学报, 1989, 11(2): 143-147.Liu Shuchun, Xu Jiqian. The Workspace and Flexibility of Industrial Robot[J]. Journal of University of Science and Technology Beijing, 1989, 11(2): 143-147.[4]王兴海, 周超. 机器人工作空间的数值计算[J]. 机器人, 1988, 2(1): 50-53.

Wang Xinghai, Zhou Chao. DigitalCalculation of Workspace for a Robot Manipulator[J]. Robot, 1988, 2(1): 50-53.

[5]袁泉. 喷浆机器人的工作空间分析[J]. 机械科学与技术, 2001, 20(1): 62-63.

Yuan Quan. An Analysis of the Work-space of a Spray Robot[J]. Mechanical Science and Technology, 2001, 20(1): 62-64.[6]Rastegar J,Fardanesh B.Manipulator Workspace Analysis Using the Monte Carlo Method[J].Mechanism& Machine Theory,1990,25(2):233-239.[7]钟勇,朱建新. 机器人工作空间求解的新方法[J]. 凿岩机械气动工具, 2003(4): 11-13.

Zhong Yong, Zhu Jianxin. ANew Method of Solving the Robot Workspace[J]. Mechanical Pneumatic Rock Drill Tools, 2003(4): 11-13.

[8]赵燕江，张永德，蒋金刚，等. 基于Matlab的机器人工作空间求解方法[J]. 机械科学与技术， 2009, 28(12): 1656-1666.

Zhao Yanjiang, Zhang Yongde, Jiang Jingang, et al. AMethod for Solving Robot Workspace Based on Matlab[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(12): 1656-1666.

[9]刘晓宇，路小龙，赵世平. 电力铁塔攀爬机器人工作空间的3种求解方法[J]. 机械设计，2012,29(5): 10-14.

Liu Xiaoyu, Lu Xiaoong, Zhao Shiping. ThreeMethods for Solving Power Tower Climbing Robot Workspace[J]. Journal for Machine Design, 2012, 29(5): 10-14.

[10]David G A, Chung-Ching D N. Determining Manipulator Workspace Boundaries Using the Monte Carlo Method and Least Squares Segmentation[C]//23rd ASME Mechanisms Conference.Minneapolis:ASME,1994: 141-146.[11]曹毅，王树新，李群智. 基于随机概率的机器人工作空间及其解析表达[J]. 组合机床与自动化加工技术，2005(2)：1-4.

CaoYi,WangShuxin,LiQunzhi.GenerationofManipulatorWorkspaceBoundaryGeometryUsingtheProbabilisticMethodandItsAnalyticalDescription[J].ModularMachineTool&AutomaticManufacturingTechnique, 2005(2): 1-4.

[12]印峰，王耀南，余洪山. 基于蒙特卡罗方法的除冰机器人作业空间边界提取[J]. 控制理论与应用，2010,27(7)：891-896.

YinFeng,WangYaonan,YuHongshan.WorkspaceBoundaryExtractionofDe-icingRobotBasedonMonteCarloMethod[J].ControlTheory&Applications, 2010, 27(7): 891-896.

[13]赵杰，王卫忠，蔡鹤皋. 可重构机器人工作空间的自动计算方法[J]. 天津大学学报，2006，39(9)：1082-1087.

ZhaoJie,WangWeizhong,CaiHegao.AlgorithmsforAutomaticallyDeterminingWorkspaceofReconfigurableRobots[J].JournalofTianjinUniversity, 2006, 39(9): 1082-1087.

[14]BrezovnikS,GotlihK,BalicJ,etal.OntheDesignofWorkspacesofSerialMechanisms[C]//13thWorldCongressinMechanismandMachineScience.Guanajuato,México, 2011: 1-8.

[15]GianniC,ErikaO,MarcoC.AFairlyGeneralAlgorithmtoEvaluateWorkspaceCharacteristicsofSericalandParallelManipulators[J].MechanicsBasedDesignofStructuresandMachines:AnInternationalJournal, 2008,36: 14-33.

[16]杨文珍，梁春辉，陈文华，等.ZATU拟人灵巧手设计与仿真[J]. 系统仿真学报，2011，23(12)：2617-2622.

YangWenzhen,LiangChunhui,ChenWenhua,etal.DesignandSimulationofZSTUAnthropomorphicRobotHand[J].JournalofSystemSimulation, 2011, 23(12): 2617-2622.

[17]熊有伦. 机器人学[M]. 北京：机械工业出版社，1993.

(编辑郭伟)

A New Method for Workspace Boundary Extraction for Jointed Serial Robot

Hou Yulei1Wang Changmei2Hu Xinzhe1Zeng Daxing1Zhao Yongsheng1

1.Yanshan University,Qinhuangdao,Hebei,066004 2.Dongfang Electric Machinery Co.,Ltd.,Deyang,Sichuan,618000

Based on the principles of bar limit combined with fixed joint variable, a new method for the workspace boundary extraction——“limit fixed interval angle” was proposed. The ideas and implementation steps was illuminated. Taking the ABB robot as an example, the link parameters and joint variables were set with D-H method. In addition, the transformation relation between the robot coordinate system and D-H coordinate system was established, from which the key point of workspace was obtained. Using MATLAB software, the three dimensional perspective workspace of the robot in the wrist was drew. A comparative analyses reveal that the accuracy of the boundary keypoint satisfies the standard of the commercial robots completely. The method presented herein is simple, effective, easy to calculate and manipulate. The research fruit of workspace of the serial robot possesses important theoretical guiding significance and practical application value.

serial robot; workspace; boundary; limit fixed interval angle

2014-05-19

国家科技重大专项(2010ZX04004-112)；河北省自然科学基金资助项目(E2012203034)

TP24DOI：10.3969/j.issn.1004-132X.2015.03.005

侯雨雷，男，1980年生。燕山大学机械工程学院副教授、博士。主要研究方向为并联机构学、多维力传感器技术、人形机器人关节仿生等。王嫦美，女，1987年生。东方电气集团东方电机有限公司工艺部水轮发电机组助理工程师。胡鑫喆，女，1987年生。燕山大学机械工程学院硕士研究生。曾达幸，男，1978年生。燕山大学机械工程学院副教授、博士。赵永生(通信作者)，男，1962年生。燕山大学机械工程学院教授、博士研究生导师。