一种基于SOM神经网络的污水处理工艺方案比选方法

曹　荣　王仁雷

（华电电力科学研究院，浙江杭州　310030）

一种基于SOM神经网络的污水处理工艺方案比选方法

曹荣王仁雷

（华电电力科学研究院，浙江杭州310030）

目前越来越多的电厂开始应用城镇污水处理厂出水作为生产用水水源，而其出水水质直接取决于所采用的污水处理工艺。本文尝试将自组织神经网络模型应用于城镇污水处理工艺方案的决策，实例分析结果证明模型和方法是实用、有效的。且与常规比选方法相比，该模型编程简洁，实现容易，效率更高。

城镇污水处理厂自组织神经网络方案比选

1　引言

图1　自组织映射神经网络模型

表1　4种工艺方案和理想方案及淘汰方案的评价指标方案

目前越来越多的电厂开始应用城镇污水处理厂出水作为生产用水水源，而其出水水质直接取决于所采用的污水处理工艺。城镇污水处理厂工艺方案比选是一个十分复杂的系统分析问题，涉及经济、技术、社会、生态环境等诸多因素，而这些因素各自的属性不同、重要性差异较大，许多因素的评价结果难于定量化［1］。近年来国内外许多学者对该问题进行了研究，提出了灰色关联度比选模型［2-3］、层次分析法［4-5］、模糊数学评价模型［6-8］、物元分析模型［9］等众多方法，对城镇污水厂工艺方案比选起到了积极的作用。但是鉴于城镇污水处理工程关系重大，而现有方法各有其缺陷，因此在进行工艺方案比选时，有必要采用多种方法进行评估，综合比较，从而得出较为客观与合理的结论。为此，本文提出一种新的比选方法，即自组织映射（Self-Organizing Mapping，简称SOM）神经网络模型进行工艺方案的比选，以求丰富和完善城镇污水处理工艺方案比选的模型和方法。

2　自组织映射神经网络原理

自组织映射模型（SOM）是由芬兰学者Kohonen于1982年提出的，这种网络能模拟大脑脑皮层自组织的功能，它是一种竞争式学习网络，能无监督地进行自组织学习。自组织映射神经网络模型如图1所示，它由两层神经元构成，即输入层和竞争层（输出层），没有隐含层。输入层的神经元排成一列，其个数由输入网络的向量个数而定，竞争层（输出层）的若干神经元排成一个二维阵列。输入层与竞争层之间实行全互连接，竞争层的神经元之间还实行侧抑制连接。

Kohonen认为当一个神经网络接收外界输入模式时，将会分为不同的区域，各区域对输入模式具有不同的响应特征，同时这一过程是自动完成的。各神经元的连接权值具有一定的分布，最近的神经元互相诱导，而较远的神经元则相互抑制，而更远一些的则具有较弱的诱导作用。这样某个输出结点能对某个模式作出特别的反应以代表该模式，而且二维平面上相邻的结点能对实际模式分布中相近的模式作出特别的反应。当某数据模式输入时，对其某点给予最大的诱导。以指示该类模式所属区域，而同时对该点周围的点也给予较大的诱导。因此，自组织映射神经网络的输出状况，不但能判断输入模式所属的类别并使输出结点代表某一模式，还能够得到整个数据区域的大体分布情况，即从样本数据中抽取到所有数据分布的大体本质特征。总之，自组织特征映射神经网络是一种无教师的聚类方法，它能将高维模式映射到一平面上，而保持其拓扑结构不变，亦即距离相近的模式点，其映射点的距离也相近。其学习过程可描述为：对于每一个网络的输入，只调整一部分权值，使权向量更接近或更偏离输入矢量，这一调整过程，即为竞争学习。随着不断学习，权矢量在输入空间相互分离，形成了各自代表输入空间的一类模式，即实现了聚类功能。SOM神经网络的详细内容见文献［10-11］。下面给出这种模型的通用算法：

（1）初始化：将权值向量Wi用小的随机值进行初始化。设置初始学习速率η（0）。

（2）采样：从输入空间中选取训练样本X。

（3）近似匹配：通过欧式距离最小的标准：

来选取获胜神经元c，从而实现了神经元的竞争过程。

（4）更新：对获胜神经元拓扑邻域Nc（n）内的兴奋神经元，以Hebb学习规则：

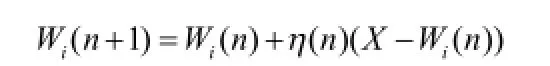
更新神经元的权值向量，从而实现神经元的合作和更新过程。

（5）更新学习速率η（n）及拓扑邻域Nbi（n），其中一种更新方法为：

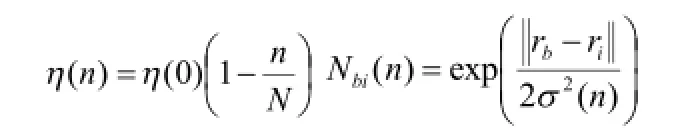
式中rb和ri分别是输出单元b和i在映射平面的位置；σ（n）反映了邻域的范围。η（n）是可变学习速度，随迭代次数的增加而减小。也就是说，随着训练过程的进行，权值的调整幅度越来越小。Nbi（n）也随着迭代次数而收缩，当n足够大时，只训练获胜结点本身。η（n）和Nbi（n）有多种不同的表达形式，在具体训练过程中可以根据不同的要求不同的数据分布进行设计。

（6）判断迭代次数n是否超过N，如果n≤N，转到第二步，否则结束迭代过程。

3　实例研究

3.1实例概况

南方某城镇污水处理厂的设计规模为5×104m3/d，工艺方案准备在三沟式氧化沟、SBR法、A2/O法和AB法4种工艺中选择，并依次记为方案1、方案2、方案3、方案4。选择的评价指标有工艺技术成熟度、费用现值（主要为主体构筑物和污泥处理部分的基建投资和运行电费现值之和）、占地面积、操作管理、出水稳定性和除磷脱氮效果6项。除费用现值和占地面积根据概算得到外，其余4项模糊指标经多位专家打分后取平均值得到。最后得到4种工艺方案和理想方案（记为方案5）及淘汰方案（记为方案6）的评价指标值，如表1所示。数据来自文献［3］。

3.2原始数据预处理

城镇污水处理工艺方案决策的影响因素错综复杂，包括多个评价指标。由于各评价指标量纲不一，范围大小差别较大，因此有必要对评价指标原始数据作预处理，以改善数据质量，保证工艺方案的可比性。常见的数据预处理方法有均值中心化、对数变换、正规化变换和标准化处理等，其中标准化处理方法是应用最广泛和最有效的数据预处理技术。本文就选用该方法对评价指标原始数据作预处理。变换公式为：

由层次分析法得到6项评价指标的权重为［0.3269，0.3269，0.0639，0.1165，0.1019，0.0639］，数据来自文献［3］。按照式（1）、式（2）对评价指标原始数据进行标准化处理，再乘以相应的权重得到样本矩阵X（输入SOM网络时需要进行转置）。

3.3模型建立与方案比选

按照SOM原理，首先将上述的各个方案标准化和加权后的评价指标矩阵（转置后）作为输入样本，则输出为各个方案的分类，然后根据分类结果进行排序，从中选出最优方案。

利用MATLAB6.5神经网络工具箱［12］编制了一个程序，主要过程如下：

（1）确定输入样本，此处输入样本是标准化和加权后方案的评价指标集。

（2）利用神经网络工具箱函数newsom建立一个SOM网络，先确定竞争层（输出层）的神经元个数为两个，即将方案分为2类（优类与劣类）。

（3）利用train函数对网络进行训练，最大训练次数定为500次。

（4）最后通过sim函数实现输入样本的分类。

运行上述自编的程序，得到输出结果为：

式（3）中括弧内第1个数字为神经元编号，第2个数字为方案编号。即方案1、方案3、方案6在第2个神经元响应，它们属于同一类，方案2、方案4、方案5在第1个神经元响应，它们也属于同一类。由于方案5是理想方案，方案6是淘汰方案，故方案2和4要优于1和3。

由于还没有选出最优方案，需要利用SOM网络对样本进行进一步的细分。考虑将竞争层（输出层）的神经元个数定为3个，即将方案分为3类（优类、中类和劣类）。

运行程序得到输出为：

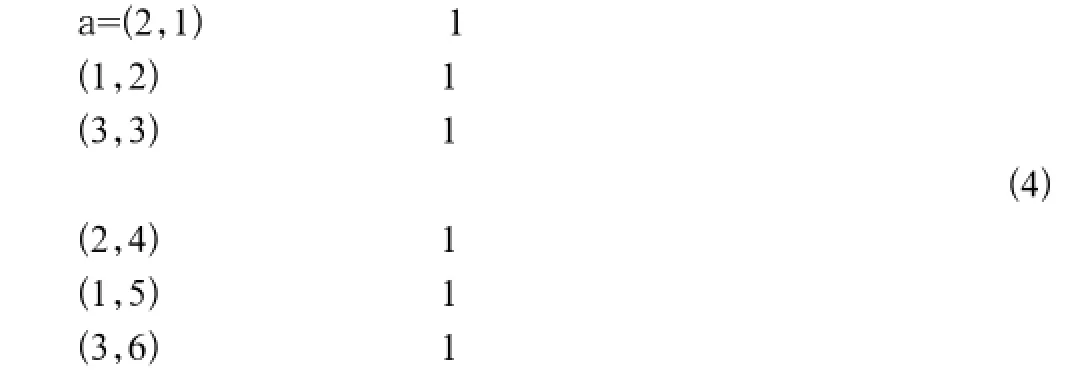
可见方案2和5为一类，方案1和4为一类，方案3和6为一类。综合以上两次分类所得结果可以知道方案2是最优方案，方案3是最差方案，4个方案的排序是2＞4＞1＞3，即SBR法＞AB法＞三沟式氧化沟＞A2/O法。故本方法推荐的比选方案是SBR法，这与实际结果是一致的，同时与文献［3］灰色关联度法比选的结果也是一致的。

4　结论与建议

（1）利用自组织神经网络模型对城镇污水处理工艺方案进行比（2）建立自组织神经网络模型时，利用MATLAB软件的神经网络工具箱进行编程，简洁方便，且实现较为容易，比常规比选方法效率更高。

选，实质是一个对候选方案与理想开发方案及淘汰方案进行模式识别的过程，实例证明它是合理的、可行的，该方法也适用于其它类似问题的比选决策。

（3）由于城镇污水处理工艺方案的比选关系重大，因此可同时考虑几种决策方法，对它们的结果进行综合比较，从而得到更为客观、合理的方案。

［1］周律，米金套，吴春旭，等.中小城镇污水处理投资决策与工艺技术［M］.北京：化学工业出版社，2002.

［2］凌猛，杭世珺.城镇污水处理厂工艺方案模糊决策方法的应用［J］.给水排水，1998，24（3）：6－9.

［3］王浙明，史惠祥，苏雨生，等.灰色关联模型用于工程方案优化［J］.中国给水排水，2002，18（1）：81－84.

［4］胡天觉，陈维平，曾光明，等.运用层次分析法对株洲霞湾污水处理厂污水处理工艺方案择优［J］.环境工程，2000，18（1）：61－63.

［5］张建锋，黄廷林.关中地区污水处理工艺选择的系统分析［J］.环境工程，1999，17（3）：61.

［6］李如忠.多层次模糊综合评判模型在城镇污水处理中的应用［J］.淮南工业学院学报，2000，20（4）：1－4.

［7］鄢恒珍，龚文琪，晏全香.小城镇污水处理方案的模糊相似优先比决策模型［J］.环境科学与管理，2009，08：62-65.

［8］刘庆玉，柴丽.污水处理工艺方案的熵权模糊灰色关联优选法［J］.沈阳农业大学学报，2008.02：125-127.

［9］慕金波，酒济明.物元分析在环境工程方案评标中的应用［J］.重庆环境科学，1997，19（3）：28-32.

［10］Kohonen T. Self-Organizing Maps［M］.Spring.Berlin.1995.

［11］袁曾任.人工神经元网络及其应用［M］.北京：清华大学出版社，1999.

［12］许东，吴铮.基于MATLAB6.x的系统分析与设计—神经网络（第二版）［M］.西安：西安电子科技大学出版社，2002.

Self-organizing neural network model is used to make decision about process selection of urban WTP. An example shows that the method is effective and valuable. Compared with conventional methods of optimization，the new model is easier to program and realize.

Urban WTP；Self-organizing neural network；Project；Decision-making

曹荣（1982—），男，硕士，毕业于浙江工业大学，主要从事电力化学及环保技术研究工作；王仁雷（1980—），男，硕士，毕业于重庆大学，主要从事电力化学及环保技术研究工作。