结构参数对偶极声波换能器谐振频率的影响∗

唐 壤　吴德林　丛健生　魏 倩

（1中国科学院声学研究所声场声信息国家重点实验室　北京　100190）

（2中国科学院大学　北京　100049）

结构参数对偶极声波换能器谐振频率的影响∗

唐 壤1，2†吴德林1，2丛健生1魏 倩1

（1中国科学院声学研究所声场声信息国家重点实验室北京100190）

（2中国科学院大学北京100049）

偶极横波远探测技术在我国复杂地质结的构油气勘探中具有十分广阔的应用前景。换能器的工作频率直接影响声波测井的探测深度。本文对正交偶极声波测井换能器弯曲模态的谐振频率进行了解析计算，并利用有限元方法研究了其结构参数对谐振频率的影响。计算结果表明：当压电陶瓷片的长度增加时，换能器一阶谐振频率先降低后升高，三阶谐振频率先升高再降低之后又上升；当金属基片厚度增加时，换能器一阶与三阶谐振频率均升高；当压电陶瓷片厚度增加时，换能器谐振频率的变化方向与幅度还与压电陶瓷片长度等其他参数相关，有可能升高或降低。

声波远探测，偶极声波，声学换能器，低频

1　引言

声波远探测是利用反射声波识别井周地质构造的技术，探测范围从常规测井技术的井周1 m左右提高到几十米，该技术在我国陆相沉积盆地的油气勘探中具有十分广阔的应用前景。2004年，Tang首次提出偶极横波远探测声波成像方法，使用具有指向性的偶极声源解决了单极测量无法判断反射体方位的问题，并且借助偶极声源较低的工作频率（约2～5 kHz）获得了较高的探测深度［1-3］。

由于我国油田井下地质结构变化复杂，钻探费用高，这就需要在现有探井中进行测井作业时尽可能地提高探测范围。换能器的工作频率直接影响声波测井的探测深度。在不改变现有多极子阵列声波成像测井仪器机械结构的前提下，降低其工作频率，突出低频成分，利用横波远探测处理方法，可以提高井周的声探测范围［4］。

偶极声波测井换能器大多采用弯曲振子产生声波，这种工作模式能够在较小尺度就获得较低的工作频率。近几年，国内一些学者在偶极声波测井换能器方面做了一定的研究工作。陈雪莲采用数值方法分析了偶极声波换能器在不同边界条件下的振动模态和频率响应［5］；乔文孝等研究了边界条件对弯曲振子振动模态的影响，并对比了数值分析与实验结果［6］；郑林等利用数值方法研究了三叠片型偶极声波测井换能器，并就换能器结构参数对换能器的工作模态、谐振频率发射效率等性能指标的影响进行了讨论，其中对谐振频率的分析主要针对一阶频率［7］。由于偶极声源在低频时的辐射效率偏低［8-9］，目前换能器的实际工作通常需要一阶和三阶模态配合使用。但有关偶极子换能器三阶模态的研究还少有报道。

本文运用薄板理论推导三叠片型换能器在空气中的谐振频率。在现有正交偶极声波测井换能器机电结构的基础上，利用有限元方法研究换能器结构参数对其谐振频率的影响，并与解析解进行比较。上述研究工作的开展，对于目前正交偶极子声波测井仪器的升级改造和功能提升可提供参考依据，也有助于声波远探测仪器的研发工作。

2　三叠片型偶极声波测井换能器

三叠片型偶极声波测井换能器的基本结构如图1所示。上下两片+z方向极化的压电陶瓷，与中间金属基片黏结而成。金属基片接电源负极，压电陶瓷外侧面接电源正极，工作在长度方向弯曲振动模式。

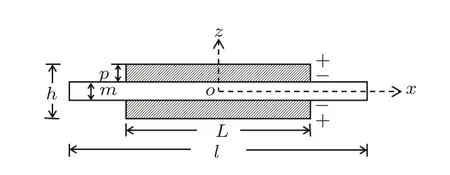
图1　三叠片型偶极声波测井换能器示意图Fig.1 Dipole trilaminar bar transducer

本文的算例以多极子阵列声波成像测井仪偶极子发射换能器（以下称参考模型）为参考，采用的压电陶瓷材料为PZT-4，金属基片材料为硬铝。参考模型中压电陶瓷片的长度为L=101 mm，宽度b=38 mm，每片厚度p=3.4 mm。金属基片总长度192 mm，考虑到两端均有打孔并以螺栓固定，有效振动长度为l=182mm，厚度m=3.2 mm，宽度仍为b。换能器总厚度为h。数值计算中金属基片两端按钳定边界处理，并忽略了粘胶、引线等装配结构。

用有限元方法模拟空气介质中三叠片的谐振频率，得到的一阶与三阶弯曲振动模态如图2（a）、2（b）所示，谐振频率分别为462 Hz、3693 Hz。

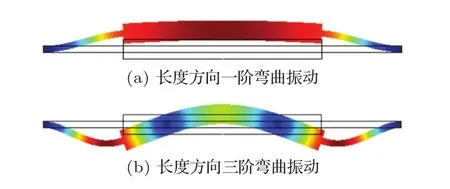
图2　换能器长度方向弯曲振动模态Fig.2　Flexural vibration of the transducer in length

3　换能器谐振频率的解析分析与有限元计算

3.1弯曲振动三叠片换能器的理论分析

应用薄板理论推导图1中三叠片型换能器的谐振频率，有以下假设条件［10-12］：（1）换能器的长度l远大于其横向尺寸b与h；（2）换能器各部分的形变看成是中性面的一边被拉长，而另一边被压缩，不考虑剪切形变；（3）只考虑换能器垂直于其中性面的位移，即挠度w，不考虑其旋转惯性。

设压电陶瓷的密度为ρp，柔性常数矩阵机电耦合系数k31。金属基片密度为ρm，柔性系数为sm。三叠片作弯曲振动。其有源部分（|x|＜L/2）为I段，其余部分（|x|＞L/2）为II段。I段满足波动方程

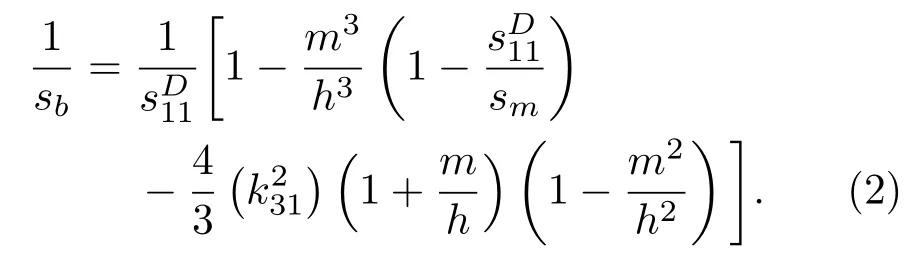
II段为无源的金属基片部分，满足波动方程［8］

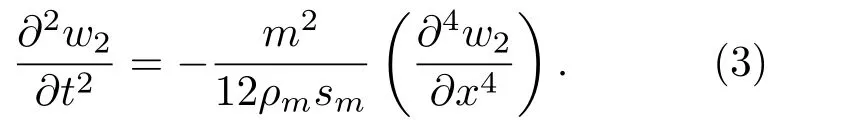
只考虑w（x）=w（-x）的对称模态，可以设

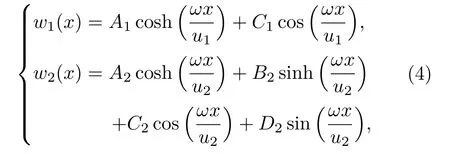
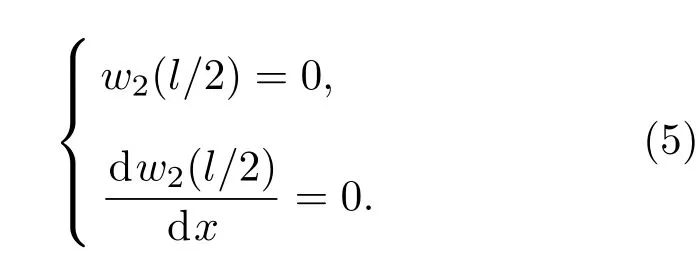
x=L/2的衔接处应满足弯曲位移、弯角、弯矩及剪应力连续［12］：

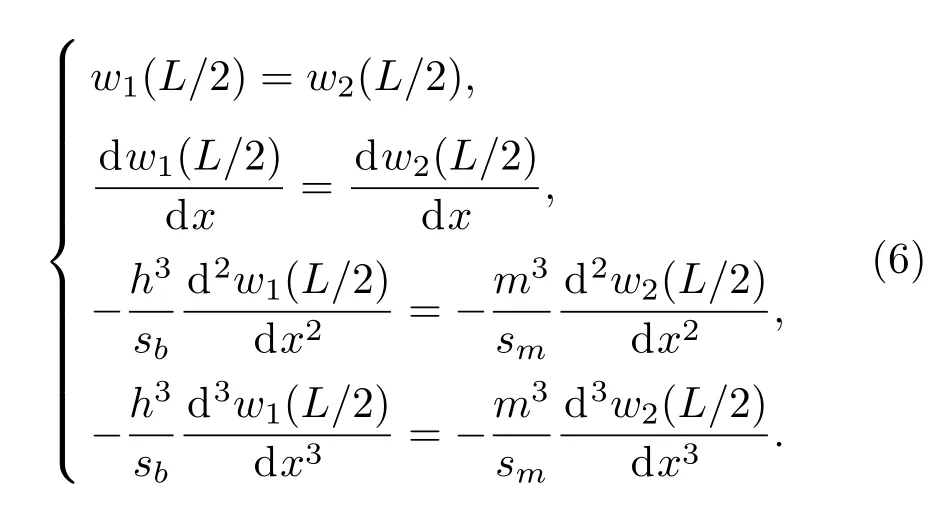
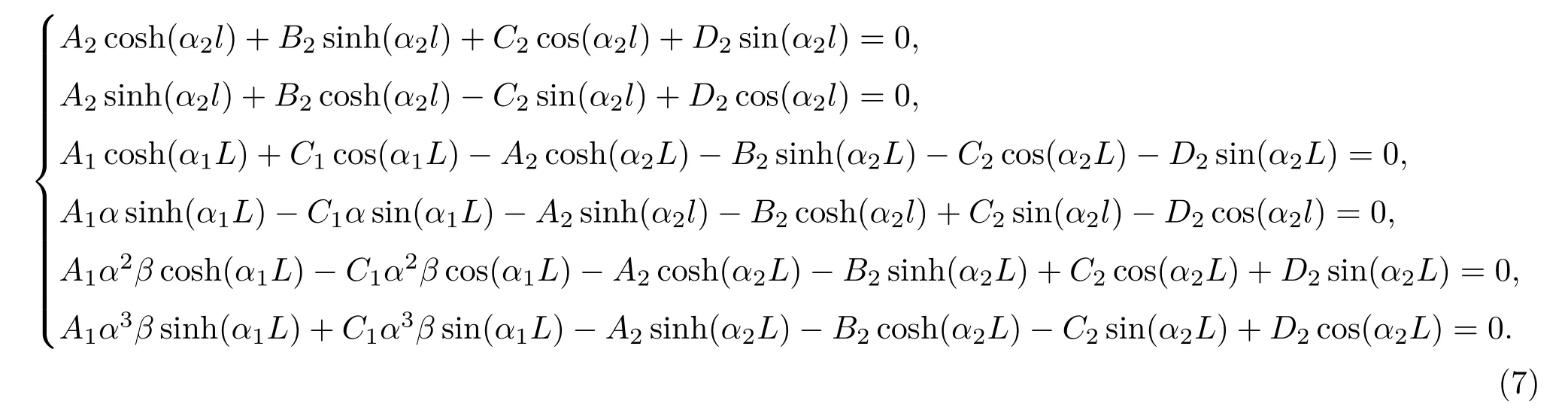
要求得A1，C1，A2～D2的非零解，需要其系数行列式为零，即

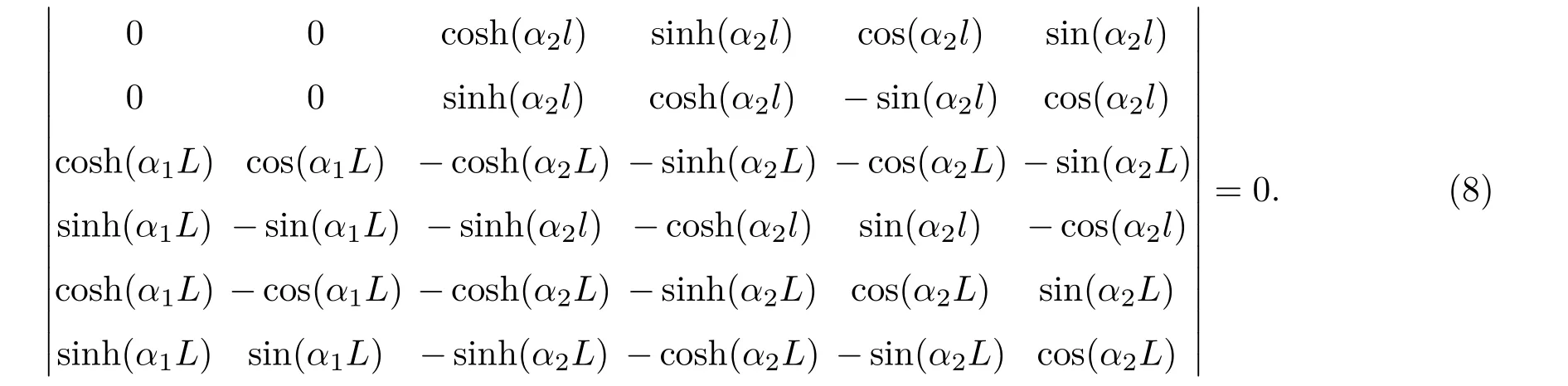
由此可解出ω进而得到三叠片的谐振频率。

3.2计算实例及结果对比

对于参考模型，根据（8）式求解其前三阶谐振频率，并与有限元计算结果进行对比，见表1。参考模型的几何尺寸和材料参数分别见表2、表3。由于上述推导中已经假定三叠片为对称振动，因此求得的均为奇数阶谐振频率。

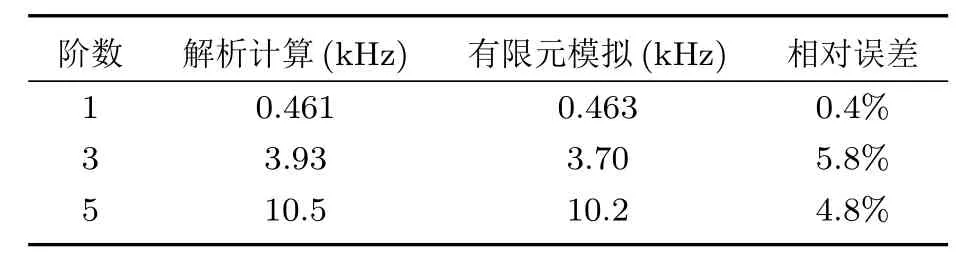
表1　参考模型谐振频率解析计算与有限元结果对比Table 1　Comparison of analytical and FEM results on reference model

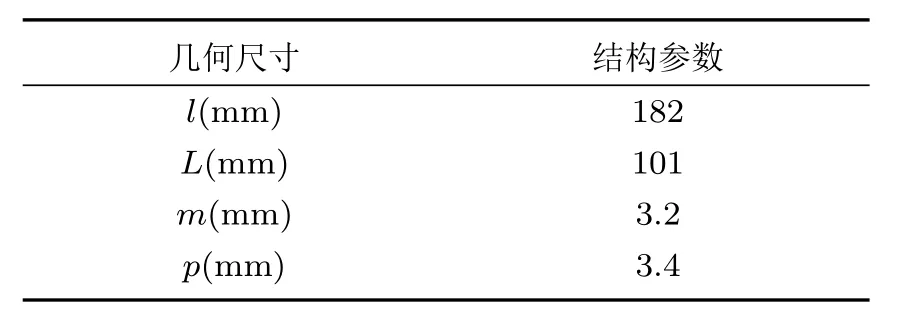
表2　参考模型尺寸Table 2 Dimensions of the reference model

表3　参考模型材料参数Table 3 Materials of the reference model

对比发现，有限元模拟与解析方法求得的基频相差很小。三阶频率误差最大，超过了5%。高阶频率的解析解与有限元模拟结果偏差较大的原因可能是波长变短，不满足薄板假设。

4　结构参数对三叠片型换能器谐振频率的影响

为使改进后的换能器可以在现有的多极子阵列声波成像测井仪器上装配使用，需要保持换能器金属基片的长度、宽度和开孔位置不变，即l、b不变。在此情况下，分别改变三叠片的金属基片厚度（m）、压电陶瓷片厚度（p）、压电陶瓷片长度（L），用有限元方法计算这三者的尺寸变化对三叠片换能器一阶与三阶谐振频率的影响。

4.1金属基片厚度、压电陶瓷片长度对换能器谐振频率的影响

首先保持压电陶瓷片厚度不变，只改变金属基片厚度（m）和压电陶瓷片长度（L），计算变化尺寸下换能器长度方向的前两阶谐振频率，关系曲线如图3。其中图3（a）、3（b）分别为一阶频率、三阶频率与金属基片厚度以及压电陶瓷片长度的关系。

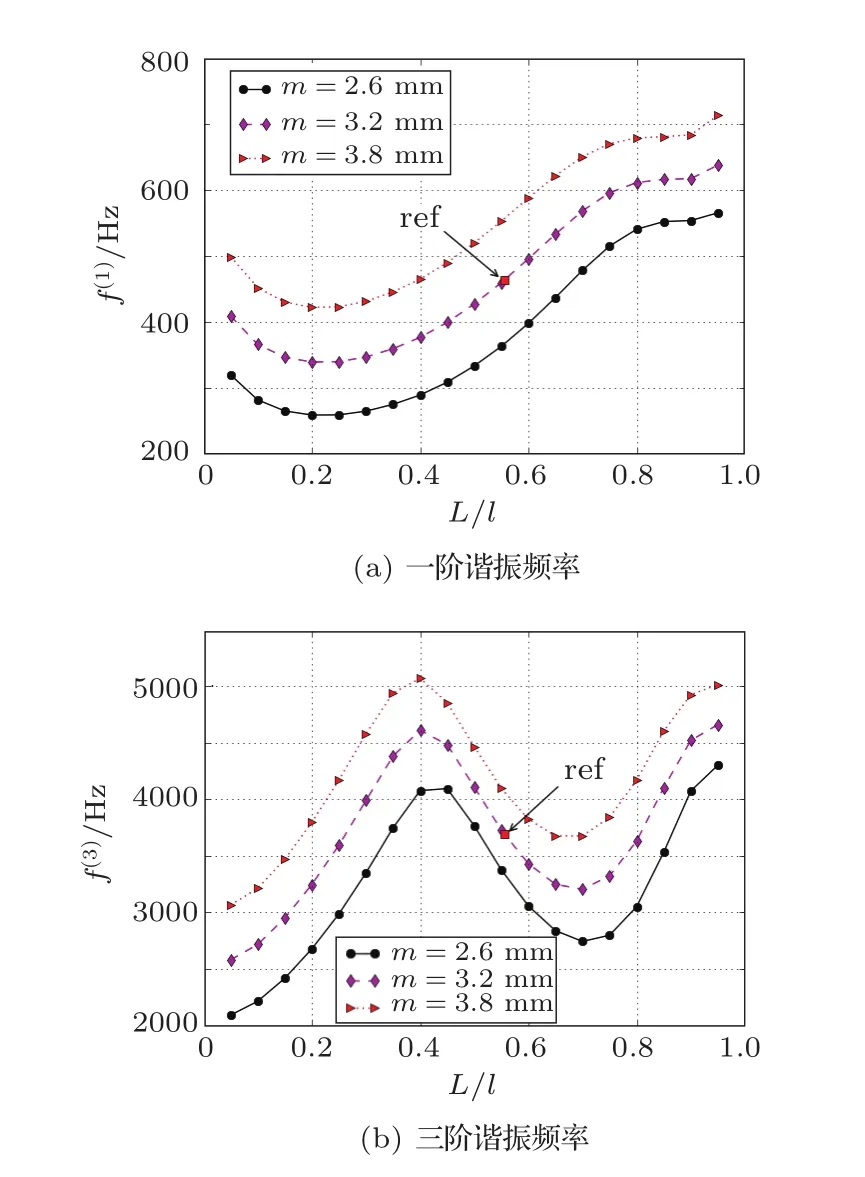
图3　换能器谐振频率与金属基片厚度和压电陶瓷片长度的关系Fig.3　Impact of thickness of metal layer and length of piezoelectric ceramics on the resonant frequencies

图3中横坐标为压电陶瓷片的长度L与金属基片有效长度l之比，每条曲线表示了换能器谐振频率随L/l的变化情况。从图3中可以看出，随着压电陶瓷片长度增加，换能器的一阶谐振频率先下降后上升；而三阶谐振频率先上升再下降，之后又上升。三阶谐振频率在L/l=0.4附近有极大值，在L/l=0.7附近有极小值。

图3中各条曲线代表金属基片厚度不同的情况下换能器的谐振频率，从下往上基片厚度依次增大。这表明换能器的一阶、三阶谐振频率均随金属基片厚度增大而增大。

4.2压电陶瓷片厚度与长度对换能器谐振频率的影响

保持金属基片厚度不变，只改变压电陶瓷片厚度（p）和压电陶瓷片长度（L），计算变化尺寸下换能器长度方向的一、三阶谐振频率，结果如图4。

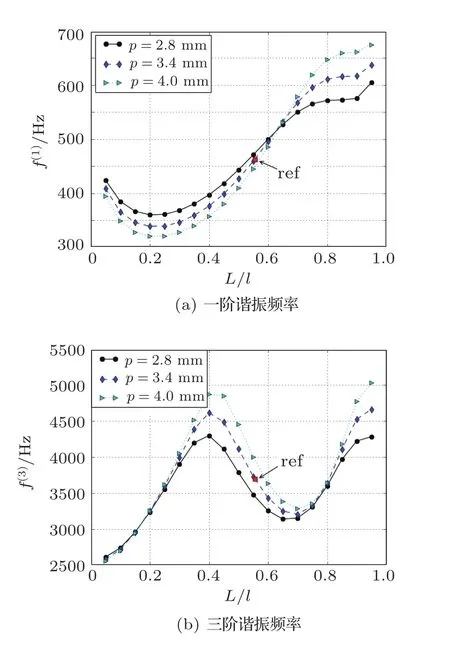
图4　换能器谐振频率与压电陶瓷片厚度和长度的关系Fig.4 Impact of thickness and length of piezoelectric ceramics on the resonant frequencies

图4中每条曲线表示了换能器谐振频率随L/l的变化情况。从图4中也可以看出，换能器的一阶谐振频率随着压电陶瓷片长度增加先下降后上升；而三阶谐振频率先上升再下降，之后又上升。这与图3的结果是一致的。

图4中各条曲线代表压电陶瓷片厚度不同的情况下换能器的谐振频率。从图4（a）可见，在压电陶瓷片长度较小时，换能器的一阶谐振频率随压电陶瓷片厚度增大而减小；压电陶瓷片长度较大时，一阶频率随压电陶瓷片厚度增大而增大。从图4（b）可见，除了在L/l很小时换能器的三阶谐振频率随压电陶瓷片厚度增大而略有减小，其余部分三阶谐振频率随压电陶瓷片厚度增大而增大，但变化的幅度还因L/l的不同而不同。

综合比较图3与图4可以发现，随着金属基片厚度增大，三叠片型换能器在长度方向的一阶与三阶谐振频率都增大；随着压电陶瓷片长度增大，换能器长度方向的一阶谐振频率先减小后增大，三阶频率先增大再减小后又增大。随着压电陶瓷片厚度增大，换能器谐振频率的变化方向还与压电陶瓷片的长度等其他参数有关，有可能增大或减小。

4.3与解析计算结果对比，压电陶瓷片长度对谐振频率的影响

改变压电陶瓷片长度L，根据方程组（7）求解换能器的谐振频率，并与有限元分析的结果进行对比。图5（a）、5（b）分别为一阶、三阶谐振频率。

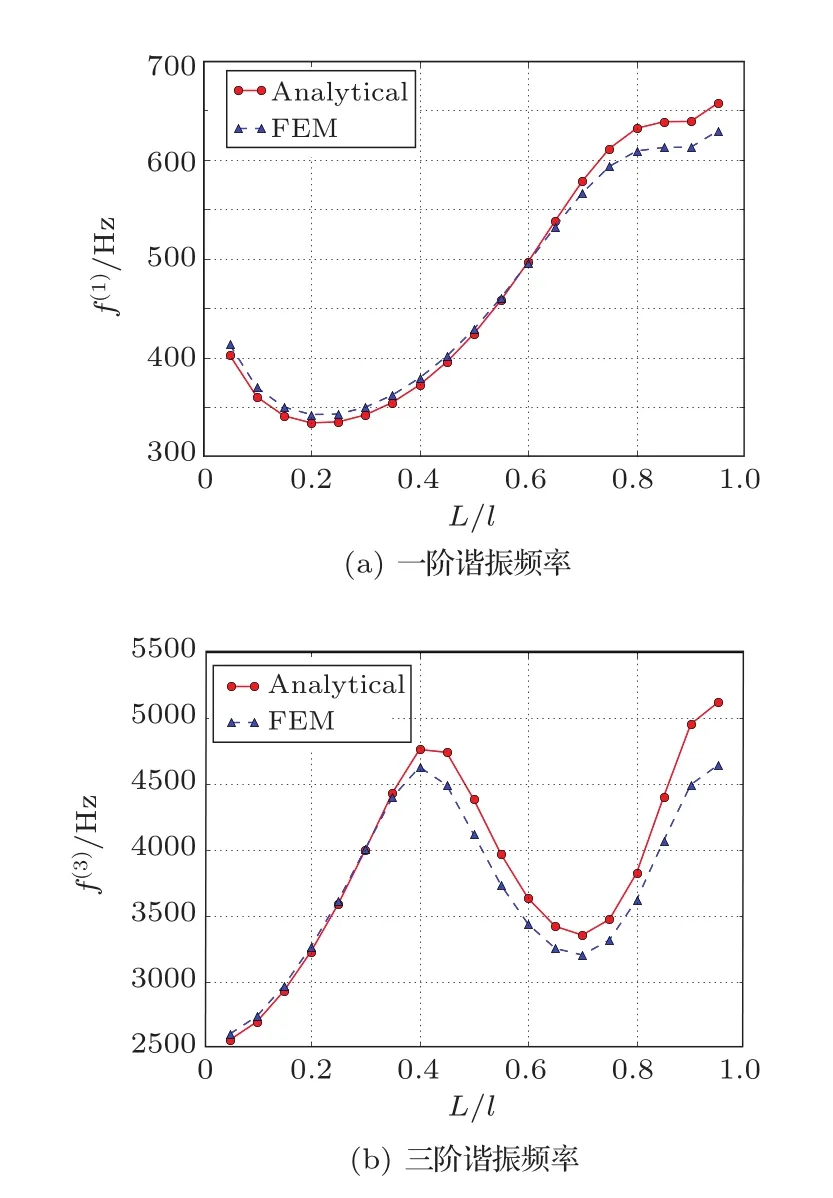
图5　换能器谐振频率与压电陶瓷片长度的关系Fig.5 Impact of length of piezoelectric ceramics on the resonant frequencies

计算结果表明，有限元分析与解析计算结果基本吻合。L/l较小时两者相差较小，L/l较大时误差略有增大。一阶频率最大误差4.3%，三阶频率最大误差9.3%。三阶谐振频率在L/l较大时误差较大，原因可能是波长与厚度之比变小，不再满足薄板理论的假设条件。

5　讨论与结论

本文对三叠片型偶极声波测井换能器在空气中的谐振频率进行了理论与数值仿真，推导了三叠片型换能器谐振频率的解析计算方法。分析了压电陶瓷片长度、厚度、金属基片厚度对换能器长度方向弯曲振动的一阶与三阶谐振频率的影响。数值分析表明，当金属基片厚度增加时，换能器一阶与三阶谐振频率均增加；随着压电陶瓷片长度增加，换能器的一阶频率先下降后上升，三阶频率先上升再下降后又上升。在原模型的基础上如要降低换能器长度方向三阶谐振频率，可适当增加压电陶瓷片长度，但不宜超过三阶谐振频率取得极小值处的长度；也可以适当减小压电陶瓷的厚度和金属基片的厚度，但考虑机械加工以及压电陶瓷电极限等因素，不宜太薄。

致谢 感谢中国科学院声学研究所王秀明研究员、张海澜研究员对本文的指导。

［1］唐晓明，魏周拓.声波测井技术的重要进展——偶极横波远探测测井［J］.应用声学，2012，31（1）：10-17. TANG Xiaoming，WEI Zhoutuo.Significant progress of acoustic logging technology：remote acoustic reflection imaging of a dipole acoustic system［J］.Applied Acoustics，2012，31（1）：10-17.

［2］唐晓明，魏周拓.利用井中偶极声源远场辐射特性的远探测测井［J］.地球物理学报，2012，55（8）：2798-2807. TANG Xiaoming，WEI Zhoutuo.Single-well acoustic reflection imaging using far-field radiation characteristics of a borehole dipole source［J］.Geophysics，2012，55（8）：2798-2807.

［3］TANG X M.Imaging near borehole structure using directionalacousticwavemeasurement［J］.Geophysics，2004，69（6）：1378-1386.

［4］辛鹏来，王东，陈浩，等.多极子阵列声波成像测井技术研究［J］.应用声学，2013，32（4）：237-245. XIN Penglai，WANG Dong，CHEN Hao，et al.Research on key technologies of multipole array sonic logging［J］. Applied Acoustics，2013，32（4）：237-245.

［5］陈雪莲.偶极声波换能器振动特性计算［J］.应用声学，2008，27（5）：407-412. CHEN Xuelian.Calculation of vibration characteristics of acoustic dipole transducer［J］.Applied Acoustics，2008，27（5）：407-412.

［6］乔文孝，车小花，张菲.边界条件对声波测井弯曲振子振动模态的影响［J］.中国科学，2008，38（增刊I）：174-179. QIAO Wenxiao，CHE Xiaohua，ZHANG Fei.The effect of boundary condition to the mode of vibration of well logging bender vibrator［J］.Science in China，2008，38（I）：174-179.

［7］郑林，林伟军，王东.三叠片型偶极声波测井换能器的有限元设计［J］.测井技术，2009，33（2）：106-109. ZHENGLin，LINWeijun，WANGDong.The design of sandwich dipole transducer based on finite element method［J］.Well Logging Technology，2009，33（2）：106-109.

［8］杜功焕，朱哲民，龚秀芬.声学基础［M］.南京：南京大学出版社，2001.

［9］张海澜.理论声学［M］.北京：高等教育出版社，2007.

［10］栾桂冬，张金铎，王仁乾.压电换能器和换能器阵［M］.北京：北京大学出版社，2005.

［11］WOOLLETT R S.The flexural bar transducer（Scientific and engineering studies）［M］.U.S.：Naval Underwater Systems Center，1986.

［12］林书玉.超声换能器的原理及设计［M］.北京：科学出版社，2004.

Impact of structure parameters on resonant frequencies of dipole transducer

TANG Rang1,2WU Delin1,2CONG Jiansheng1WEI Qian1
（1 State Key Laboratory of Acoustics，Institute of Acoustics，Chinese Academy of Sciences，Beijing 100190，China）
（2 University of Chinese Academy of Sciences，Beijing 100049，China）

Remote sensing logging using dipole shear wave has broad prospects in oil and gas exploration in China.Frequency of the transducer directly affects the detecting depth.In this paper the resonant frequencies of dipole transducer are studied with both analytical and finite element method.The effects of modifying the transducer's structural dimensions on its resonant frequencies are discussed.Results demonstrate that，as the length of piezoelectric ceramic layers increases，the 1st-order frequency increases after decreases first，while 3rd-order frequency at first increases then decreases and finally rises again.As the metal layer gets thicker，both 1st and 3rd-order frequencies increase.Impact of thickness of the piezoelectric ceramic layers on the resonant frequencies varies with other parameters.

Remote sensing logging，Dipole，Acoustic transducer，Low frequency

TB552

A

1000-310X（2015）02-0107-06

10.11684/j.issn.1000-310X.2015.02.003

2014-05-14收稿；2014-07-23定稿

∗国家自然科学基金项目（41474160）

唐壤（1989-），女，重庆人，硕士研究生，研究方向：超声换能器。

E-mail：tangrang11@mails.ucas.ac.cn