汽车非线性主动悬架系统的分数阶模糊控制

高　远　范健文　潘盛辉　李　珊　孔　峰

1.广西科技大学,柳州,545006　　2.广西科技大学鹿山学院,柳州,545616　　3.广西汽车零部件与整车技术重点实验室,柳州,545006

汽车非线性主动悬架系统的分数阶模糊控制

高远1,3范健文2,3潘盛辉1,3李珊2孔峰1

1.广西科技大学,柳州,5450062.广西科技大学鹿山学院,柳州,5456163.广西汽车零部件与整车技术重点实验室,柳州,545006

针对非线性主动悬架系统的控制问题，提出一种分数阶模糊控制方法。该方法采用分数阶微分信号作为模糊控制器输入,并根据悬架系统综合性能指标函数最小准则获得分数阶次。仿真结果表明：相比整数阶的模糊控制情形，即使车辆在不同车速和不同等级道路的行驶工况下，该分数阶模糊控制方法可以使得非线性悬架系统能够获得更优的控制效果，能进一步降低车身垂直振动加速度、动行程及轮胎形变，有效提高车辆的行驶平顺性和操纵稳定性。

车辆；非线性悬架；分数阶；模糊控制

0　引言

汽车悬架是影响汽车乘坐舒适性和操纵稳定性的重要部件。以微处理器为核心，采用电控技术的可控悬架是现代车辆悬架技术发展的重要趋势。控制策略是实现悬架系统最优控制的保证，也是当前悬架控制系统研究发展的一个重要方面[1]。车辆悬架系统可视为一个受随机路面激励的非线性系统[2],结合汽车悬架系统模型，研究者迄今提出了许多悬架系统控制方法，这些方法几乎涉及控制理论的各分支,但其各有优缺点[3]。如模糊控制法[4-5],虽然方法简单,可适用于非线性、时变和滞后系统，且具有一定的自适应能力，但其性能完全依靠专家经验设计，一旦控制器的规则及参数确定，则按特定的规则方式处理，故控制性能不能很好地适于各种行驶工况要求。为解决这些问题，目前主要采取自动调整模糊控制器中论域比例因子、量化因子或直接修改模糊关系矩阵的手段。然而，比例因子与量化因子存在相互制约影响，而后者也面临计算量较大的困难[6-7]。

自20世纪末以来,随着计算机技术的发展，分数阶微积分理论被广泛应用于物理、材料、信号处理及自动控制等领域[8]。研究发现,相比整数阶情形，分数阶的控制器能获得更优的控制性能和鲁棒性，这极大地促进了分数阶数学理论在控制领域中的应用[9]。目前,已有学者将分数阶理论应用于汽车悬架系统的设计及控制,但研究成果报道尚少。Oustloup等[10]提出CRONE悬架，采用分数阶阻尼的机械系统替代传统被动悬架中的弹簧及阻尼器，分析表明该悬架系统具有很强的鲁棒性和稳定度；为提高汽车行驶平顺性，文献[11]采用CRONE控制方法对不同荷载的悬架模型进行了控制;文献[12-13]以分数阶天棚阻尼控制的车辆悬架作为参考模型，分别提出了悬架系统的自适应控制方法和滑模主动控制方法;文献[14]采用分数阶的天棚阻尼控制策略提高了半主动非线性空气悬架系统的乘坐舒适性。

本文首先建立了1/4车辆非线性主动悬架系统模型，然后针对悬架系统的控制问题，提出了一种分数阶模糊控制方法。研究采用Mamdani模糊推理系统设计模糊控制器，并考虑悬架系统受冲击载荷作用，根据时间乘平方误差积分(ITSE)控制综合性能指标函数最小的准则，得到模糊控制器输入变量的分数阶微分阶次。仿真结果表明，在不同的车速和等级道路行驶工况条件下，相比传统的整数阶模糊控制，分数阶模糊控制方法可进一步降低车辆悬架的垂直振动加速度、动行程和轮胎形变，使车辆获得更好的行驶平顺性和操纵稳定性。

1　非线性主动悬架系统模型

图1所示为1/4车辆二自由度非线性汽车主动悬架系统简化模型。图中，m1和m2分别表示1/4车身质量和轮胎质量，c为悬架阻尼系数，k1和k2分别为悬架弹簧刚度和轮胎刚度,u为主动控制力,x1、x2分别为车身位移和轮胎位移，q为路面位移输入。假设悬架弹簧为非线性刚度弹簧，其产生的非线性恢复力与位移的关系为

F=k1(x1-x2)+εk1(x1-x2)3

(1)

式中,ε为弹簧的非线性系数。

图1　1/4车辆主动悬架简化模型

定义悬架阻尼力Fd为

(2)

结合图1,可建立非线性悬架系统的动力学模型如下：

(3)

非线性悬架系统模型中的系统参数如表1所示。

表1　悬架系统参数

2　悬架系统的分数阶模糊控制器设计

2.1分数阶微积分的定义

(1) 施工质量控制问题。受施工各方面条件的限制，施工质量控制是改造方案的关键所在，特别是在新浇筑道床与既有道床基础联结，以及换铺新轨枕、安装扣件并浇筑恢复整体道床后，白天行车产生的振动和冲击才是影响施工质量的关键因素。

分数阶微积分运算是整数阶微积分理论的推广，整数阶情形是分数阶微积分的特例[9]。对于分数阶微积分算子，可定义为

(4)

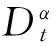
(5)

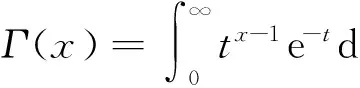
图2　悬架系统的分数阶模糊控制原理

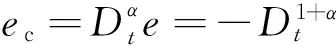
本文采用Mamdani模糊逻辑推理系统设计模糊控制器[17],该控制器的结构及主要特点如下。

(1)模糊控制器的输入变量分别为e和ec，其对应的模糊语言变量分别为E和EC；输出是悬架系统的模糊控制作用力u，对应的模糊语言变量为U。

(2)E、EC和U的模糊集均为{负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)}。

(3)E、EC和U的论域分别为：{-0.3,-0.2,-0.1,0,0.1,0.2,0.3}、{-3,-2,-1,0,1,2,3}、{-1050,-700,-350,0,350,700,1050}。

(4)e、ec和u的隶属函数均采用Z型、sigmoid型及三角形函数相结合。

(5)所建立的模糊推理规则见表2。当输入e、ec到模糊控制器，模糊化所得到的模糊输入变量根据表2进行模糊推理产生模糊输出。表2反映出当误差绝对值朝增大的方向变化时，可根据误差大小分别实施较强或一般的反馈控制作用，以抑制动态误差；而当误差朝绝对值减小的方向变化时，可采取保持等待措施，这符合专家控制的负反馈设计思想。

(6)解模糊化方法采用面积重心法，通过解模糊得到非线性悬架的模糊控制力u。

(7)当分数阶微分阶次α=1时,则对应传统的整数阶模糊控制情形。

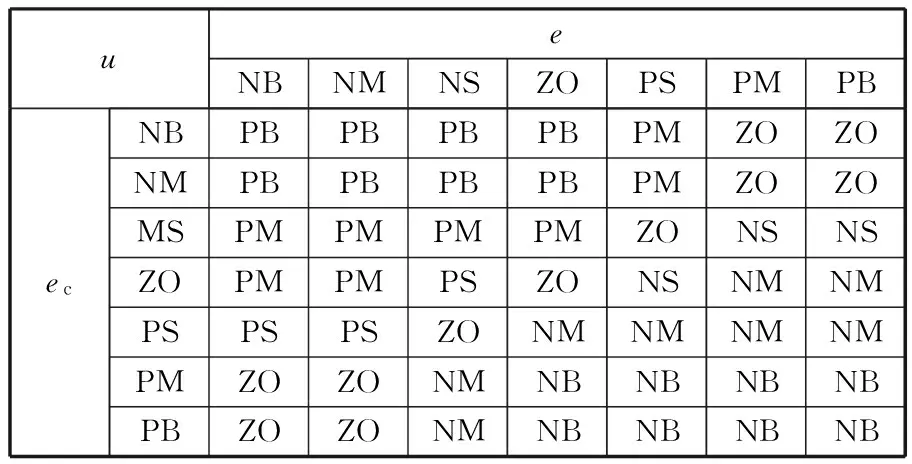
表2　模糊推理规则表

2.3分数阶微分参数的选取

(6)

式中,w1、w2、w3分别为垂直振动加速度、悬架动行程和轮胎形变的加权系数。

根据各指标的重要程度以及其本身的数量级,确定加权系数分别为w1=5×102,w2=1×104,w3=4×105。考虑车辆非线性悬架系统受图3所示的路面冲击载荷作用[18],并基于ITSE综合性能指标函数最小原则，利用MATLAB优化工具箱的fmincon命令对控制器的α参数在(0,1]范围内进行最优搜索。优化过程中的分数阶微分数值计算采用Oustaloup滤波算法实现[19]。

图3　冲击载荷波形图

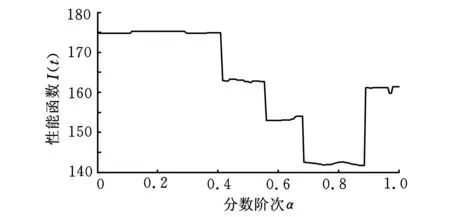
图4　综合性能指标函数与分数阶次的关系曲线

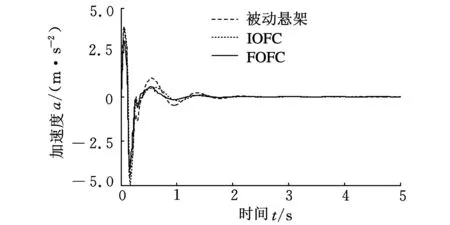
图5　垂直加速度响应曲线

图6　动行程响应曲线

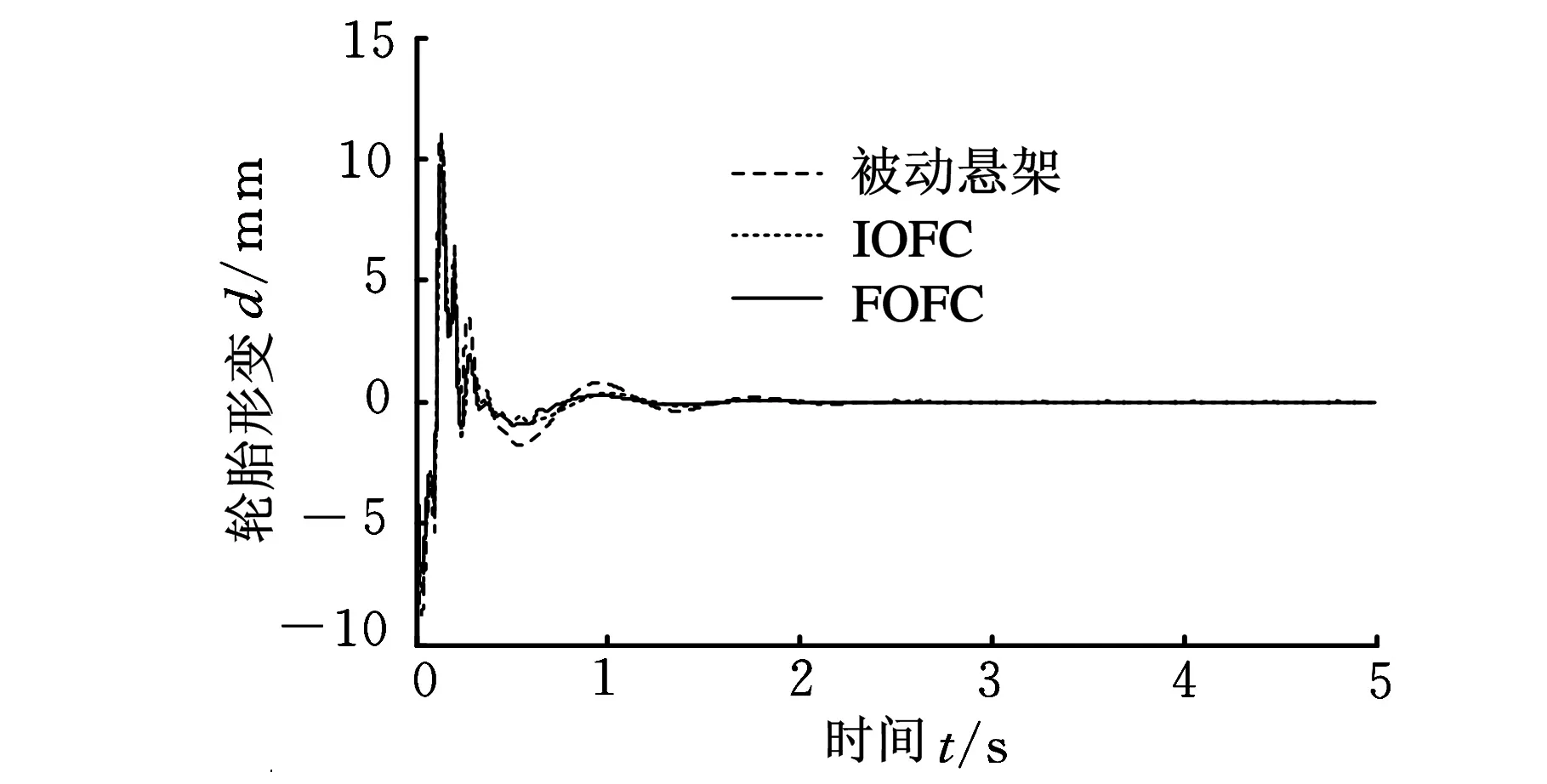
图7　轮胎形变响应曲线

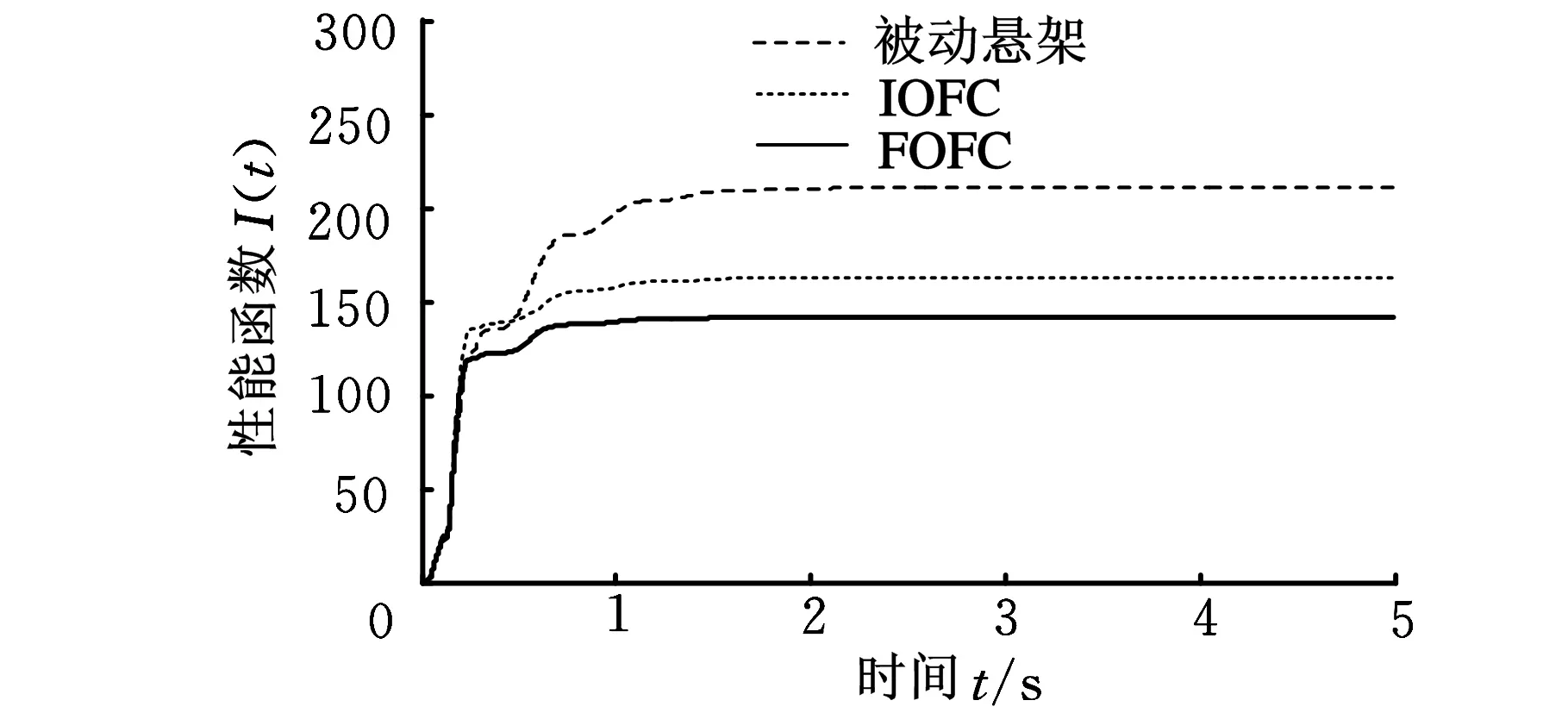
图8　综合性能指标函数曲线

3　仿真结果及分析

基于MATLAB/Simulink环境,将非线性悬架系统模型、分数阶模糊控制器以及路面输入模型模块化程序实现。仿真中分数阶微分数值计算仍采用Oustaloup滤波算法，路面激励q则通过噪声滤波方法产生[20]。为验证分数阶模糊控制方法的有效性和先进性，仿真中考虑汽车不同车速及等级路面的多种行驶工况，以及对比被动悬架、整数阶模糊控制的控制效果。

当车辆在B级路面以60 km/h速度行驶时，图9～图11分别示出了车身垂直振动加速度、悬架动行程和轮胎形变的时域响应曲线。表3～表5分别给出了不同等级路面和车速行驶工况情况下，车身振动加速度、悬架动行程和轮胎形变的均方根值，并同时列出相比被动悬架情形，不同控制方法降低对应指标的百分比。由这些图表可见，整数阶模糊控制较被动悬架而言，在B级道路行驶时，车身垂直加速度改善程度不高，甚至轮胎形变出现恶化现象，这反映模糊控制按照所确定的规则方式进行处理，控制性能不能很好适于各种行驶工况要求；然而，在相同的模糊控制器规则及参数条件下，相比整数阶控制情形，分数阶模糊控制在各种行驶工况均能进一步改善车身振动加速度、悬架动行程和轮胎形变，可有效提高车辆的行驶平顺性和操纵稳定性。这也表明分数阶模糊控制方法由于增加了可调的分数阶微分阶次参数α,使得控制器控制被控对象更加灵活，通过合理设计α参数,可以使悬架系统控制性能适于各种行驶工况要求。

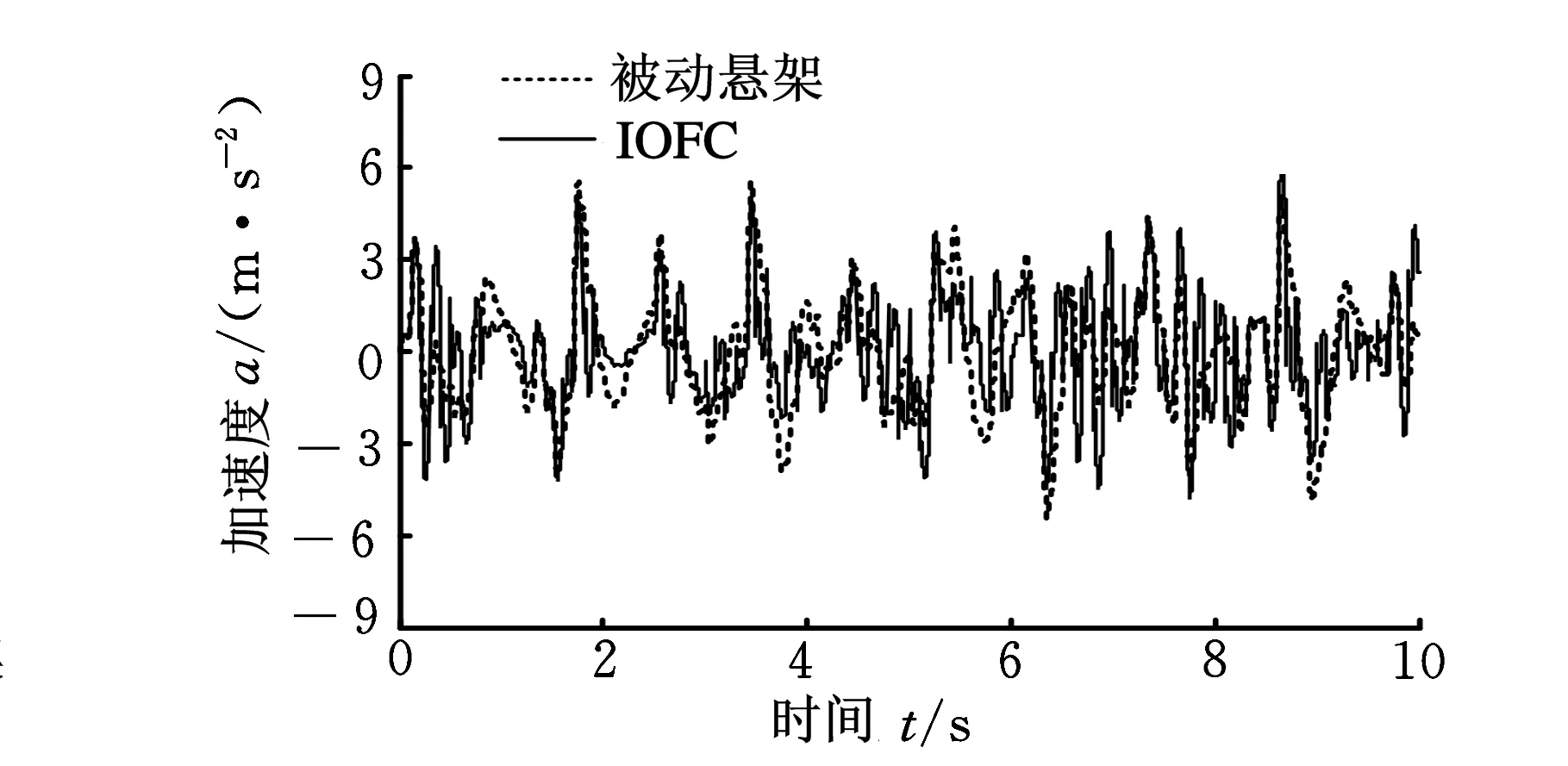
(a)整数阶模糊控制

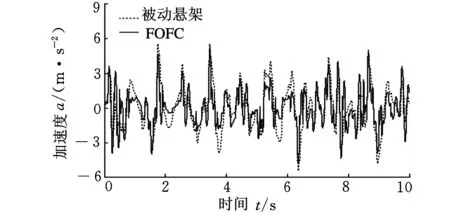
(b)分数阶模糊控制图9　振动加速度响应曲线

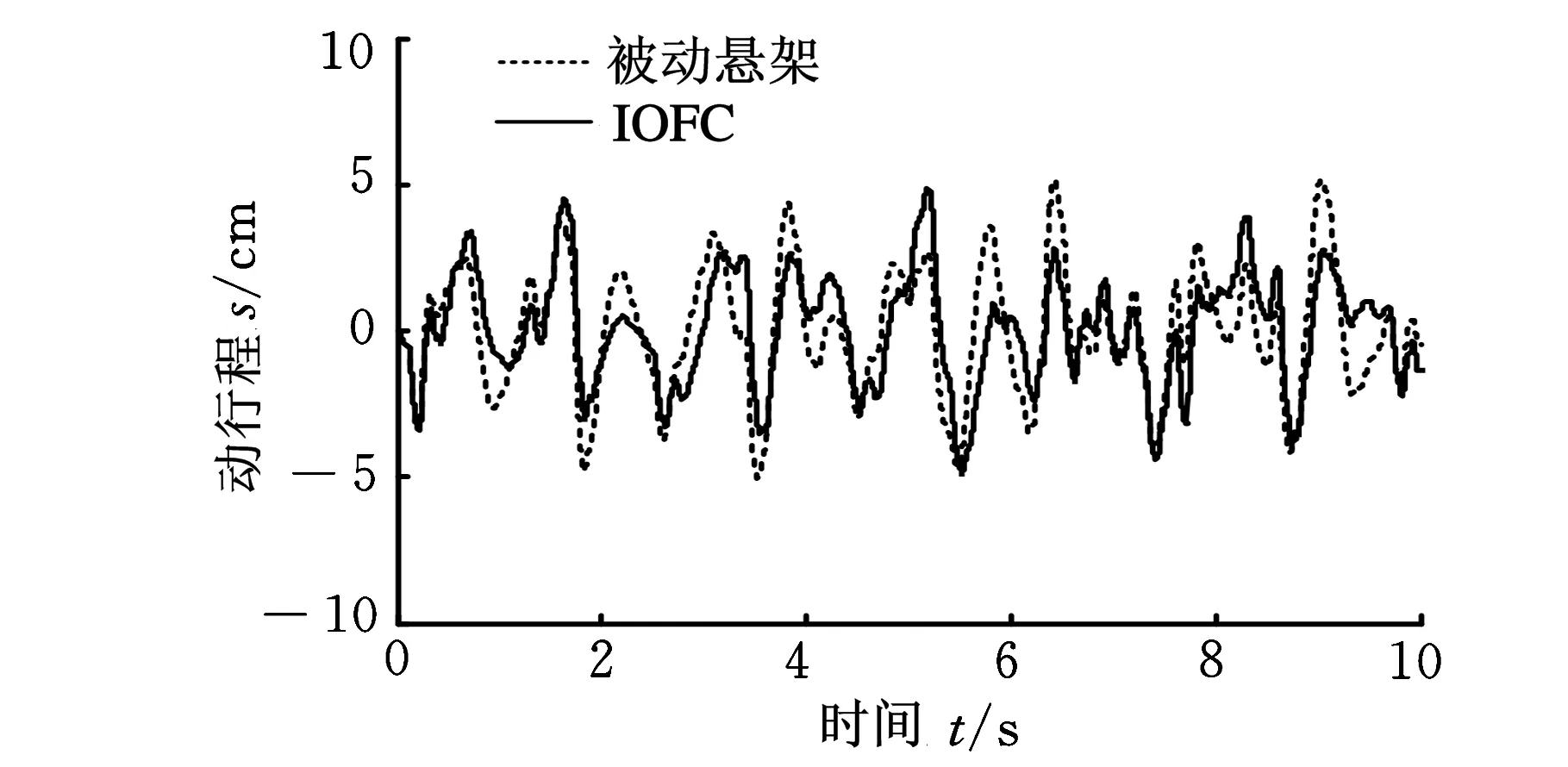
(a)整数阶模糊控制

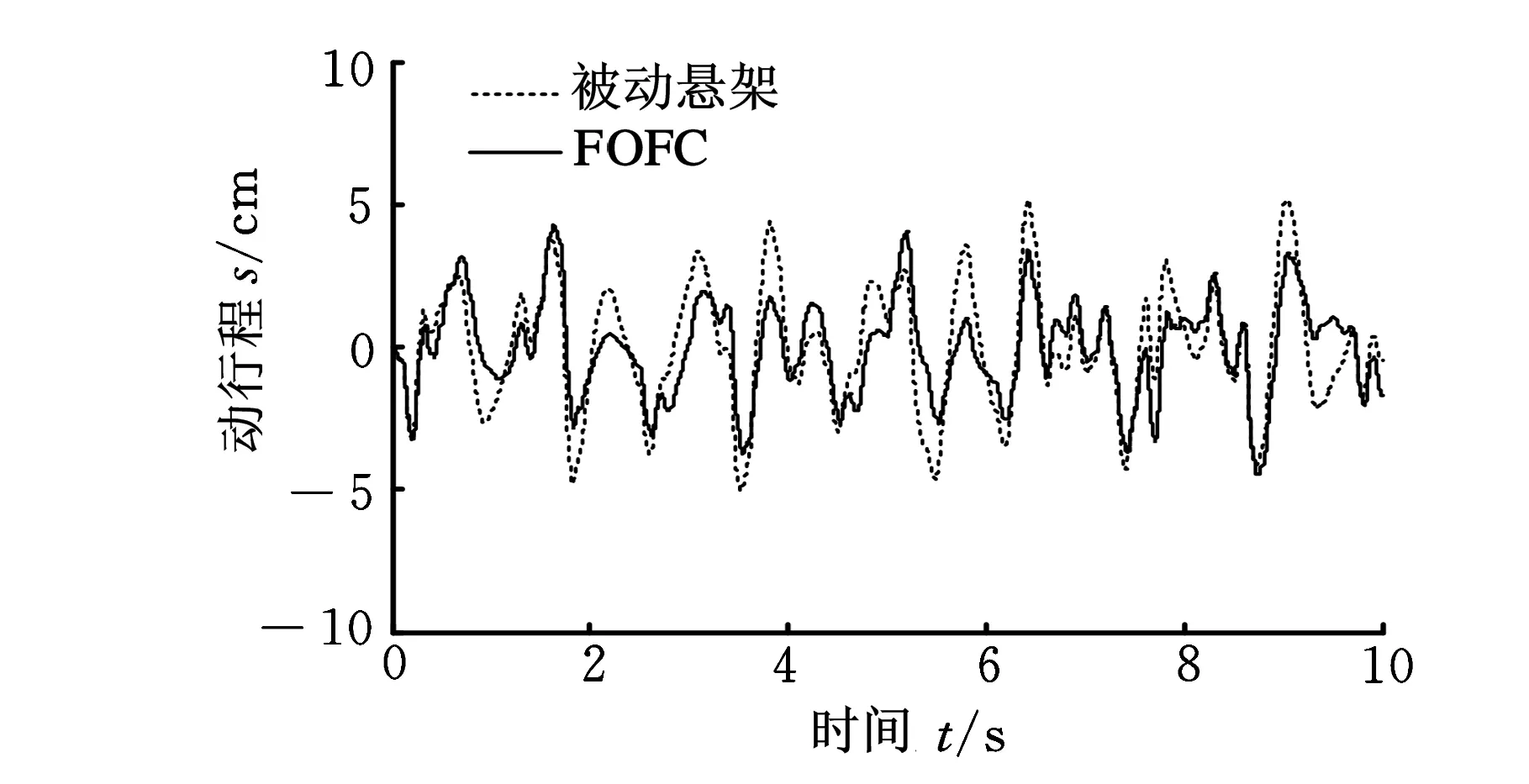
(b)分数阶模糊控制图10　悬架动行程响应曲线

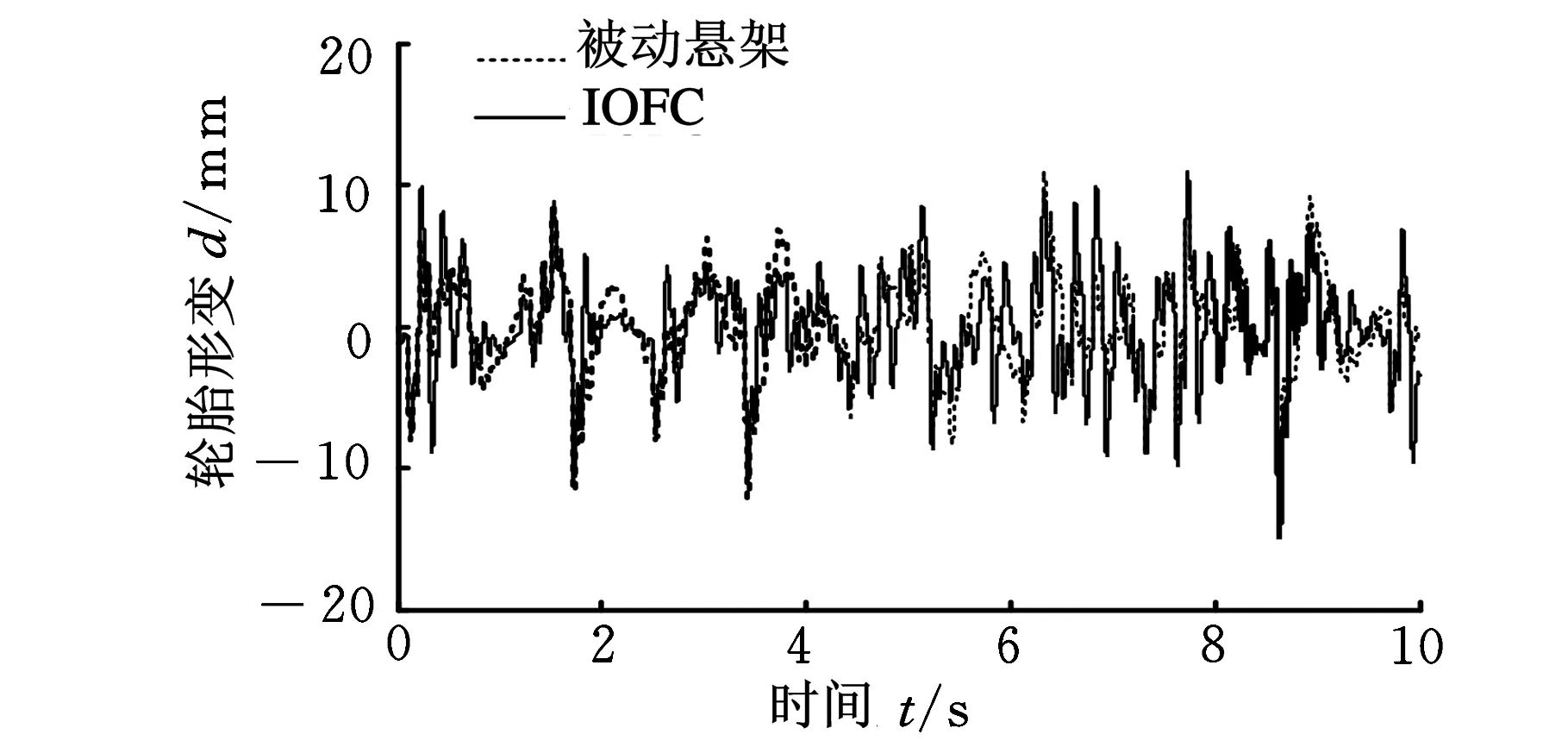
(a)整数阶模糊控制

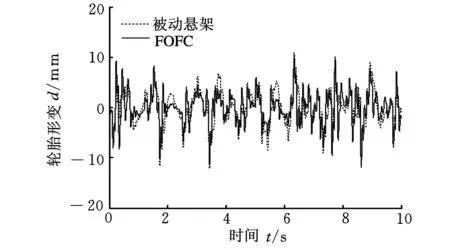
(b)分数阶模糊控制图11　轮胎形变响应曲线

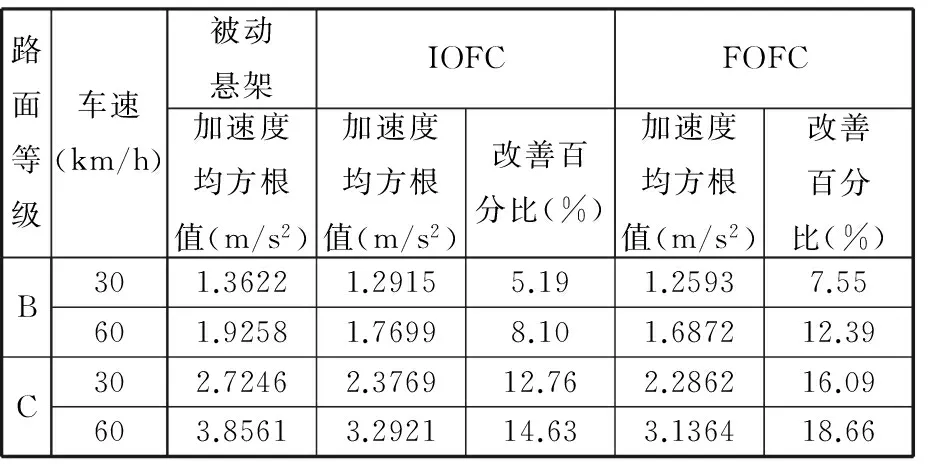
路面等级车速(km/h)被动悬架IOFCFOFC加速度均方根值(m/s2)加速度均方根值(m/s2)改善百分比(%)加速度均方根值(m/s2)改善百分比(%)BC306030601.36221.29155.191.25937.551.92581.76998.101.687212.392.72462.376912.762.286216.093.85613.292114.633.136418.66

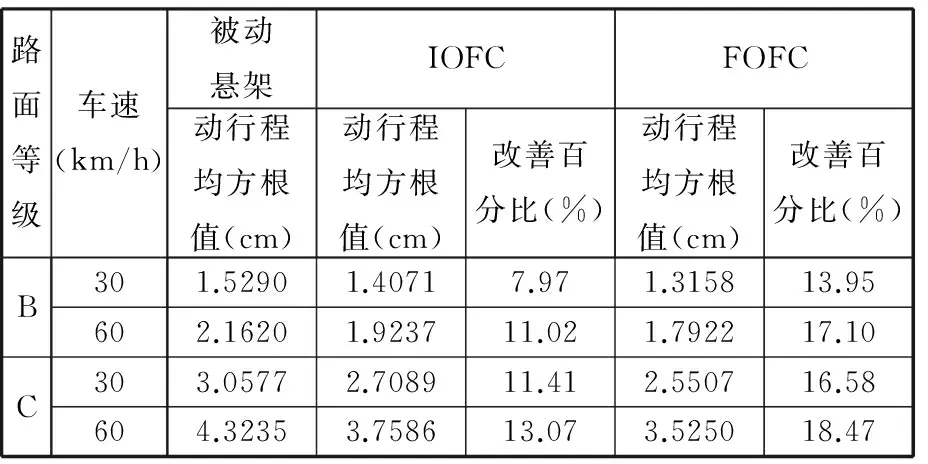
表4　悬架动行程均方根值及其改善百分比

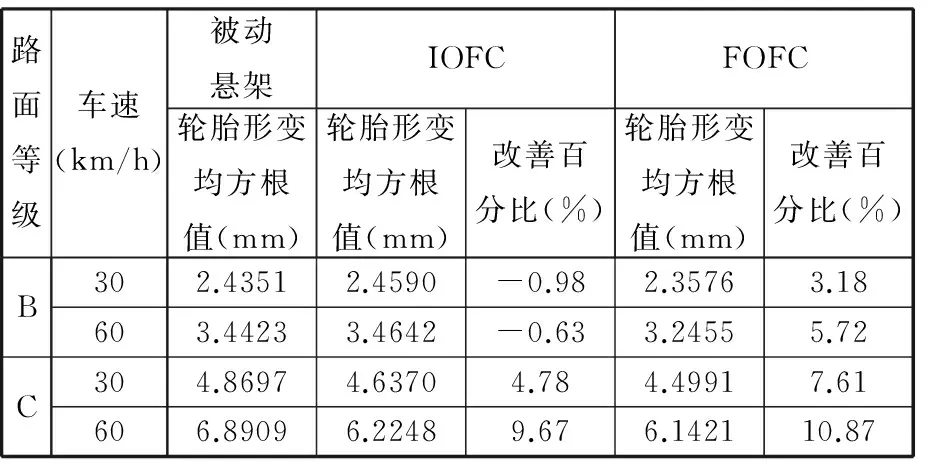
表5　轮胎形变均方根值及其改善百分比

4　结论

(1)非线性主动悬架系统的分数阶模糊控制方法将分数阶微分信号量作为模糊控制器输入,其中的分数阶微分阶次参数根据悬架系统的ITSE综合性能函数最小准则搜索计算得到，可避免传统模糊控制优化方法中论域比例因子和量化因子关系相互制约,以及修改模糊关系矩阵计算量较大的困难。

(2)仿真结果表明,相比整数阶模糊控制，在相同的模糊规则及参数条件下，分数阶模糊控制方法能进一步降低车身垂直振动加速度、悬架动行程和轮胎形变，使得悬架系统控制性能适于各种行驶工况要求，使车辆获得更好的行驶平顺性和操纵稳定性。

(3)分数阶微积分运算可采用微处理技术实现，随着高速微处理器及模糊控制芯片的发展，该方法有利于工程试验，因此研究结果为探索可控悬架系统控制策略,提高汽车行驶性能，提供了新的、有效可行的方法参考。

[1]高国生,杨绍普,郭京波.汽车悬架控制系统研究动态与展望[J].机械强度,2003,25(3):279-284.

Gao Guosheng,Yang Shaopu,Guo Jingbo.Surview and Prespect in Research of Controlling System on Automobile Suspension[J].Journal of Mechanical Strength,2003,25(3):279-284.

[2]Verros G,Natsiavas S.Ride Dynamics of Nonlinear Vehicle Model Using Component Mode Synthesis[J].Journal of Vibration and Acoustics,2002,124(3):427-434.

[3]周长城.汽车平顺性与悬架系统设计[M].北京:机械工业出版社,2011.

[4]Son S,Isik C.Application of Fuzzy Logic Control to an Automotive Active Suspension System[C]//Fuzzy Systems,Proceedings of the Fifth IEEE International Conference.New Orleans,La,USA,1996,1:548-553.

[5]Ozgur D,Ilknur K,Saban C.Modeling and Control a Nonlinear Half-vehicle Suspension System:A Hybrid Fuzzy Logic Approach[J].Nonlinear Dynamics,2012,67:2139-2151.

[6]冯宏娟,王守觉.直接修改控制规则的自调整模糊控制器[J].电子学报,1992,20(2):10-16.

Feng Hongjuan,Wang Shoujue.On Self-organizing Fuzzy Control Algorithm with Regulating the Control Rules Directly[J].Acta Electronica Sinica,1992,20(2):10-16.

[7]孙建民.基于LMS自适应滤波的模糊控制主动悬架研究[J].汽车工程,2004,26(4):472-475.

Sun Jianmin.Fuzzy Control for Vehicle Direction Adaptive PID Control Based on Single Neural Cell[J].Automotive Engineering,2004,26(4):472-475.

[8]Bohannan G W.Analog Fractional Order Controller in Temperature and Motor Control Applications[J].J. Vib. Control,2008,14(9):1487-1498.

[9]朱呈祥,邹云.分数阶控制研究综述[J].控制与决策,2009,24(2):161-169.

Zhu Chengxiang,Zou Yun.Summary of Research on Fractional-order Control[J].Control and Decision,2009,24(2):161-169.

[10]Oustloup A,Moreau X,Nouillant M.The Crone Suspension Control Engineering Practice[J].Journal of The International Federation of Automatic Control,1996,4(8):1101-1108.

[11]Altet O,Moreau X,Moze M, et al. Principles and Synthesis of Hydractive CRONE Suspension[J].Nonlinear Dynamics,2004,38:435-459.

[12]陈宁,陈南,王乃洲,等.基于分数阶参考模型的车辆悬架自适应控制[J].南京林业大学学报(自然科学版),2009,33(3):116-120．

Chen Ning,Chen Nan,Wang Naizhou,et al.Adaptive Control of Vehicle Suspension Using Fractional Order Reference Models[J].Journal of Nanjing Forestry University(Natural Science Edition),2009,33(3):116-120．

[13]陈宁,台永鹏,陈南.分数微积分理论在非线性车辆悬架滑模控制中的应用[J].动力学与控制,2009,7(3):258-264.

Chen Ning,Tai Yongpeng,Chen Nan.Application of Fractional Calculus Theory Sliding Mode Control for Vehicle Suspension Systems with Nonlinearities[J].Journal of Dynamics and Control,2009,7(3):258-264.

[14]吴光强,黄焕军,叶光湖.基于分数阶微积分的汽车空气悬架半主动控制[J].农业机械学报,2014,45(7):19-25.

Wu Guangqiang,Huang Huanjun,Ye Guanghu.Semi-active Control of Automotive Air Suspension Based on Fractional Calculus[J].Transactions of the Chinese Society for Agricultural Machinery,2014,45(7):19-25.

[15]Oldham B,Spanier J.The Fractional Calculus[M].New York:Academic,1974.

[16]Sakman L,Guclu R,Yagiz N.Fuzzy Logic Control of Vehicle Suspensions with Dry Friction Nonlinearity[J].Sdhan,2005,30(10):649-659.[17]韩峻峰,模糊控制技术[M].重庆:重庆大学出版社,2000.[18]Demir O,Keskin I,Cetin S.Modeling and Control of a Nonlinear Half-vehicle Suspension System:a Hybrid Fuzzy Logic Approach[J].Nonlinear Dyn.,2012,67:2139-2151.

[19]薛定宇.控制系统计算机辅助设计[M].2版.北京：清华大学出版社,2006.

[20]喻凡.车辆动力学及其控制[M].北京:人民交通出版社,2003.

(编辑王艳丽)

Fractional-order Fuzzy Control Method for Vehicle Nonlinear Active Suspension

Gao Yuan1,3Fan Jianwen2,3Pan Shenghui1,3Li Shan2Kong Feng1

1.Guangxi University of Science and Technology,Liuzhou,Guangxi,545006 2.Lushan College of Guangxi University of Science and Technology,Liuzhou,545616 3.Guangxi Key Laboratory of Automobile Components and Vehicle Technology,Liuzhou,Guangxi,545006

A fractional-order fuzzy control method was presented for vehicle nonlinear active suspension.This new scheme used a fractional-order differential signal as one of the control inputs,and the fractional order was obtained based on the minimum criteria of the suspension system comprehensive performance index function.Simulation results demonstrate that under the driving cycles with various grade roads and vehicle speeds,comparing with the traditional integral-order fuzzy control method,the presented method has better control performances including further reducing body acceleration,suspension travel and tyre deflection,and can improve the ride comfort and handling stability of vehicle effectively.

vehicle;nonlinear suspension;fractional-order;fuzzy control

2014-07-17

广西自然科学基金资助项目(2013GXNSFAA019351,2010GXNSFA013024);广西教育厅科研项目(201202ZD068,201204LX657);广西高等学校特色专业及课程一体化建设项目(GXTSZY234)

TP13；U463.33DOI：10.3969/j.issn.1004-132X.2015.10.023

高远，男,1975年生。广西科技大学电气与信息工程学院教授。主要研究方向为车辆动力学及控制。发表论文30余篇。范健文(通信作者),男,1963年生。广西科技大学鹿山学院副教授。潘盛辉,男,1971年生。广西科技大学电气与信息工程学院副教授。李珊,女,1988年生。广西科技大学鹿山学院助教。孔峰,男,1947年生。广西科技大学电气与信息工程学院教授。