基于RQA与GG聚类的滚动轴承故障识别

张淑清　包红燕　李　盼　李新新　姜万录

燕山大学河北省测试计量技术及仪器重点实验室，秦皇岛，066004

基于RQA与GG聚类的滚动轴承故障识别

张淑清包红燕李盼李新新姜万录

燕山大学河北省测试计量技术及仪器重点实验室，秦皇岛，066004

提出递归定量分析与GG聚类相结合的滚动轴承故障识别方法。利用能够表征信号发散程度的RQA参数——确定率和分层率组成轴承故障识别的特征向量，结合GG模糊聚类实现滚动轴承故障模式识别。对实际故障数据进行分析，结果表明，该方法不仅能够识别滚动轴承的不同程度损伤，而且能够实现不同部位的轴承故障诊断。研究结果为滚动轴承故障识别提供了一种高效、直观的新方法。

故障诊断；递归图；递归定量分析；GG模糊聚类

0　引言

滚动轴承作为旋转机械中的广泛通用部件，其缺陷和损伤将直接影响设备的稳定运行甚至造成整个设备的损坏，因此滚动轴承的故障诊断与识别极为重要[1]。故障诊断通常包括两步：第一步是故障特征参数的提取；第二步是故障类型的诊断。

滚动轴承故障信号所呈现出的非线性和非平稳特性，使得传统的建立在信号平稳性基础上的故障特征提取方法受到限制，而递归定量分析(recurrence quantification analysis, RQA)方法是在改进递归图基础上，能够量化递归图中表现出来的系统递归现象的一种方法。该方法不受数据统计分布假设的限制，能够克服传统方法对过程平稳的严格要求[2]，因此利用RQA提取轴承信号中隐含在噪声中的故障特征参数，能获得其他方法难以得到的可靠结论。

故障类型识别比较常用的方法是模糊聚类[3-4]。在众多的聚类算法中，模糊C均值(fuzzy C-means，FCM)聚类和GK(Gustafson-Kessell)聚类在工程实际中都得到了广泛应用，但FCM只适合于具有相同形状和方向的数据结构，只能反映超球形数据结构的标准距离规范(各向同性)[5]；GK算法引进了自适应距离范数和协方差矩阵，可以反映数据沿任意方向或子空间的分散程度，但该方法并没有改变聚类算法产生类似于球体的聚类状态。因此这两种聚类算法只能产生类似于球体的聚类状态。

由于数据的分布不可能总是类似于球形，本文采用GG(Gath-Geva)聚类，引入基于模糊最大似然估计的距离测度，使聚类形状不受体积的限制，以适应非规则分布数据的模糊聚类[6]。

1　递归定量分析

滚动轴承故障识别第一步是故障特征参数的提取。递归图(recurrence plot,RP)是以图形的方式定性地表征系统的动力学特性，描述重构的轨迹是如何递归或者重复其自身的。利用RQA提取轴承信号中隐含在噪声中的故障特征参数，能获得其他方法难以得到的可靠结论。

在进行递归图分析前，需先对时间序列进行相空间重构[7]。

选取最优的延迟时间τ和嵌入维数m。以时间序列{x(n)，n=1,2,…,N}为例，重构后的序列为

X(n)=(x(n),x(n+τ),…,x(n+(m-1)τ))

(1)

递归图中的点由下列矩阵确定:

Ri,j=Θ(ε-‖xi-xj‖)

(2)

i,j=1,2,…,N-(m-1)τ

其中，ε为参考阈值，本文选取ε=0.15，‖xi-xj‖为重构相空间中任意两点间的距离，Θ(·)为Heaviside函数(若x<0，则Θ(x)=0；若x>0，则Θ(x)=1)，则矩阵Ri,j由0和1组成。以i作为横坐标，以j作为纵坐标绘出Ri,j所得到的图形即为递归图。

递归图只能在二维平面内展现其递归行为，对系统动力学特性进行定性分析,无法定量描述。针对这一缺陷，Webber等[8]提出了递归定量分析方法，该方法对递归图中表现出来的递归现象进行了量化。RQA的主要非线性特征量包括递归率(RR)、确定率(DET)、递归熵(ENTR)、分层率(LAM)、平均对角线长度(L)和递归次数(TT)等。其中确定率和分层率能够表征信号发散程度，两者越接近1，发散度越低，表明信号的随机性越小，处于相对有序状态。本文选取这两个参量作为故障识别的特征向量，分析不同状态下各振动信号的差异。

确定率和分层率的计算方法如下[9-10]：

(1)确定率(DET)是构成平行于对角线线段的递归点点数与总的递归点数的比值，即

(3)

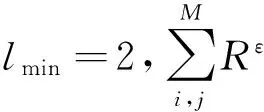
(2)分层率(LAM)是垂直线段递归点点数与所有垂直结构包含的递归点点数的比值，即

(4)

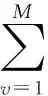
2　GG模糊聚类

滚动轴承故障识别第二步是故障类型的诊断，即利用所提取的特征参数来判别信号的归属类别。不同故障信号的特征参数对其类别的区分作用是不同的，而GG模糊聚类对非规则分布数据非常适用。因此，本文采用GG模糊聚类对所有的特征参数进行有效性分析，以提高识别效率。

GG模糊聚类引入基于模糊最大似然估计的距离测度，具体算法如下：

(1)把给定的数据集X={X1,X2,…,Xn}分成c(2≤c≤n)类，其中每个样本Xj均有q个特征向量，则分类结果可以用划分矩阵U=[uij]c×n表示，其中，i=1,2,…,c；j=1,2,…,n；uij表示第j个待分类对象属于第i类的隶属度。

(2)选定终止容差ε，ε>0，随机的初始化隶属矩阵U(0)。

(3)计算聚类中心：

(5)

(4)计算最大似然估计引入的距离测度：

Dij(Xj,vi)=

(6)

(7)

(5)更新分类矩阵:

(8)

直到‖U(l)-U(l-1)‖<ε。

通常通过如下两个系数来判定聚类效果：

(1)分类系数：

(9)

Fca越接近1，聚类效果就越好。

(2)平均模糊熵：

(10)

Hca越接近于0，聚类效果就越好。

3　实验分析

本文实验数据来自于美国凯斯西储大学(CaseWesternReserveUniversity)电气工程实验室[11]，首先选取滚动轴承外圈分别为无故障、轻微损伤(故障点尺寸为0.1778cm)、中等损伤(故障点尺寸为0.3556cm)三种状态下的振动数据为研究对象。故障点均位于6点钟方向，损伤深度均为0.2794cm。电机转速为1797r/min，负载为1492W，振动信号采样频率为12kHz。

滚动轴承外圈损伤尺寸的不同，会导致损伤引起的振动信号强弱不同，进而其吸引子的表现不一样，递归图的结构也不尽相同。进行递归图分析前需先对所研究数据进行相空间重构，本文采用基于样本时间序列及其替代数据的微分熵方法，同时对m和τ进行优化，避免了分别求取m和τ引起的不一致性[12]。

由微分熵求得无故障状态下的最佳嵌入维数m=2，最佳延迟时间τ=3；轻微损伤下的相空间重构参数为m=3，τ=6；中等损伤下的相空间重构参数为m=2，τ=9。则三种状态下的RP图形如图1所示。递归图中的垂直线或者水平线结构表明振动信号间歇性地存在，对角线或棋盘结构表示存在有规律的振荡。从递归图中可以定性地显示出三种状态的振动信号存在较大差异。

(a)无故障状态下的RP图

(b)轻微损伤状态下的RP图

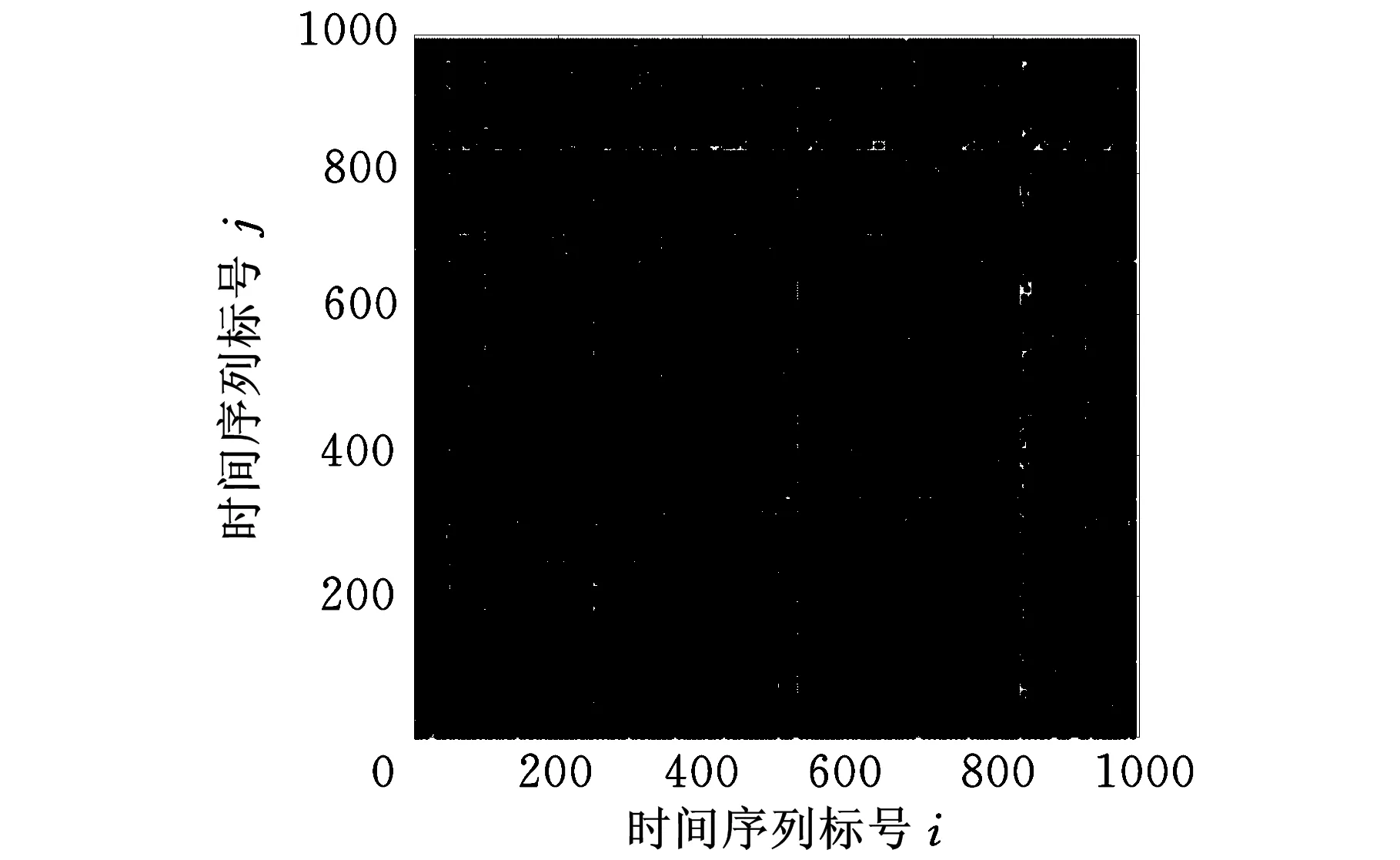
(c)中等损伤状态下的RP图图1　三种状态下的RP图

本文采用CRPTOOL[13]工具箱对三种状态振动信号进行递归定量分析，提取能将个别发散的递归点与有规律形成的特定图案的递归点区分开来的特征参数确定率(DET)和分层率(LAM)。以这两个特征参数为坐标可绘出图2。

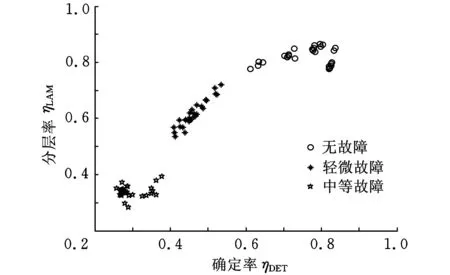
图2　不同损伤状态下的特征参数坐标图

从图2中可以看出三种状态振动信号的确定率和分层率随着损伤程度的增大而逐渐减小，表明信号发散程度逐渐增大，随机性增大，处于相对无序状态。

把确定率和分层率作为GG聚类的输入值，完成对振动信号进一步的识别和诊断。选取轴承外圈振动信号各28组，构成84×2的故障特征矩阵，聚类组数c=3，容差ε=0.0001，经迭代计算并不断更新聚类中心，直至收敛为止。GG聚类结果如图3所示，图中“O”为聚类中心。

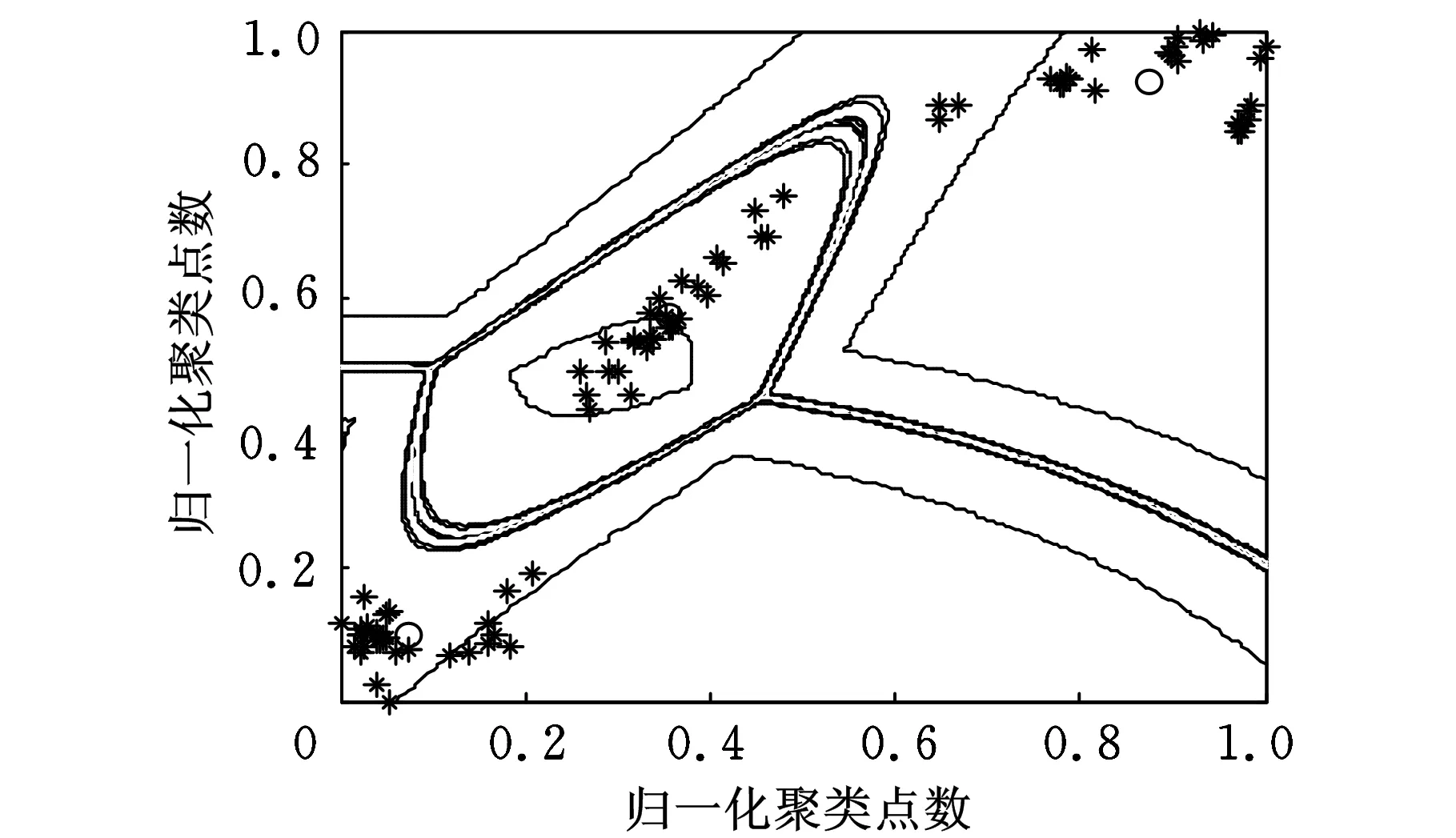
图3　GG聚类效果图

为了对三种聚类算法进行比较，分别采用FCM聚类算法和GK聚类聚类算法对三种状态下的外圈振动数据进行聚类，聚类结果如图4所示。

(a)FCM聚类效果图

(b)GK聚类效果图图4　FCM聚类和GK聚类效果图

从图中可以看出FCM聚类和GK聚类的聚类曲线都近似为圆，而GG聚类曲线不规则，能够对不同大小、形状和密度的数据分布进行聚类。为了定量表明GG聚类效果的优越性，分别计算三种聚类算法的分类系数和平均模糊熵，如表1所示。从表中可以看出GG聚类的分类系数接近于1，平均模糊熵接近于无穷小，从而证明该算法的聚类效果最好。

表1　三种聚类算法效果检验结果

依据同样的原理，对不同部位的轴承故障进行诊断实验。选取正常、滚动体故障和外圈故障三种状态下的振动数据为研究对象。损伤直径均为0.3556cm(均为中等损伤)，外圈故障点位于6点钟方向。电机转速为1797r/min，负载为1492W，振动信号采样频率为12kHz。

首先对三种状态信号进行递归图定性分析，由微分熵求得三种状态下的最佳嵌入维数和最佳延迟时间，则三种状态下的RP图形如图5所示。

从递归图中可以看出三种故障状态下的信号存在着差异，为了更准确地区别不同故障类型信号，同样采用CRPTOOL[13]工具箱对三种状态振动信号进行递归定量分析，选取确定率(DET)和分层率(LAM)作为特征参数，其坐标图如图6所示。

(a)无故障状态下的RP图

(b)滚动体故障状态下的RP图

(c)外圈故障状态下的RP图图5　三种故障状态下的RP图

图6　不同部位故障的特征参数坐标图

从图6中可以看出，三种状态振动信号的确定率和分层率存在明显区别，表明信号发散程度大不相同，随机性也有较大差异。

把两个特征参数作为GG聚类的输入值，选取滚动轴承三种状态信号各28组，构成84×2的故障特征矩阵，聚类组数为3，容差同上，经迭代计算并不断更新聚类中心，直至收敛为止。GG聚类算法的结果图如图7所示。

图7　GG聚类效果图

由于同一类型故障的不同样本之间具有相似的特点，通过RQA提取滚动轴承特征信号后，经过GG聚类处理，从图7中可以看出同一故障类型特征数据被分配到同一聚类中心周围，84组数据样本经过聚类处理后，均匀地分布到三个聚类中心周围，每一个聚类中心分布的实为同一种故障类型数据样本，且分布较为紧凑，即每个类均是紧致的，这说明RQA特征提取与GG聚类结合的方法具有极高的识别效率，同时达到了良好的故障识别效果。

4　结论

(1)提出了一种基于RQA和GG模糊聚类的故障识别方法。首先对故障信号进行递归定量分析提取特征向量参数，特征参数显示不同故障信号存在明显差异。为了进一步识别故障类型，将特征参数作为GG模糊聚类的输入向量，对滚动轴承信号进行故障识别。

(2)将GG聚类与FCM聚类和GK聚类算法进行对比，实验表明，GG聚类更适合于不规则分布数据的聚类分析，并且聚类效果也证明了GG聚类算法具有明显的优越性。

(3)分别对不同损伤故障信号和不同故障类型信号进行递归定量分析和GG模糊聚类结合的方法进行故障诊断与识别，结果表明，该方法可以完成对滚动轴承故障的诊断与识别，并且准确率高，可以作为滚动轴承故障识别的重要手段，具有一定的实际应用价值。

[1]刘卫兵,李志农,蒋静. 基于局域均值分解的滚动轴承故障诊断方法[J]. 轴承, 2009(9): 48-52.

LiuWeibing,LiZhinong,JiangJing.FaultDiagnosisMethodofRollingBearingBasedonLocalMeanDecomposition[J].Bearing, 2009(9): 48-52.

[2]赵鹏,周云龙,孙斌. 递归定量分析在离心泵故障诊断中的运用[J].振动、测试与诊断, 2010(6): 612-616.

ZhaoPeng,ZhouYunlong,SunBin.ApplicationofRecurrenceQuantificationAnalysistoFaultDiagnosisofCentrifugalPump[J].JournalofVibration,Measurement&Diagnosis, 2010(6): 612-616.

[3]LiuXF,MaL,JosephM.MachineryFaultDiagnosisBasedonFuzzyMeasureandFuzzyIntegralDataFusionTechniques[J].MechanicalSystemsandSignalProcessing, 2009,23: 690-700.

[4]FengZP,SongXG,ChuFL.FaultDiagnosisBasedonIntergrationofClusterAnalysisRoughSetMethodandFuzzyNeuralNetwork[J].ChineseJournalofMechanicalEngineering, 2004，17(3)：349-352.

[5]王书涛,张金敏,张淑清,等. 基于威布尔与模糊C均值的滚动轴承故障识别[J]. 中国机械工程, 2012,23(5): 595-599.

WangShutao,ZhangJinmin,ZhangShuqing,etal.FaultDiagnosisofRollingBearingsBasedonWeibullDistributionandFuzzyCMeansClusteringAnalysis[J].ChinaMechanicalEngineering, 2012, 23(5): 595-599.

[6]王书涛,张金敏,李圆圆,等. 基于数学形态学和模糊聚类的旋转机械故障诊断[J]. 仪器仪表学报, 2012(5): 1055-1061.

WangShutao,ZhangJinmin,LiYuanyuan,etal.RotatingMachineryFaultDiagnosisBasedonMathematicalMorphologyandFuzzyClustering[J].ChineseJournalofScientificInstrument, 2012(5): 1055-1061.

[7]严如强, 黄周弟, 钱宇宁. 基于递归定量分析法的旋转机械故障诊断[C]//2010年江苏省仪器仪表学会学术年会.徐州，2010：5-7.

[8]WebberHC,ZbilutJP.DynamicalAssessmentofPhysiologicalSystemsandStatesUsingRecurrencePlotStrategies[J].JournalofAppliedPhysiology, 1994,76:965-973.

[9]肖涵,李友荣,吕勇. 基于递归定量分析与高斯混合模型的齿轮故障识别[J]. 振动工程学报, 2011(1): 84-88.

XiaoHan,LiYourong,LüYong.GearFaultRecognitionBasedonRecurrenceQuantificationAnalysisandGaussianMixtureModel[J].JournalofVibrationEngineering, 2011(1): 84-88.

[10]尹少华,杨基海,梁政,等. 基于递归量化分析的表面肌电特征提取和分类[J]. 中国科学技术大学学报, 2006(5): 550-555.

YinShaohua,YangJihai,LiangZheng,etal.RecurrenceQuantificationAnalysisBasedonSurfaceEMGSignalFeatureExtractionandClassification[J].JournalofUniversityofScienceandTechnologyofChina, 2006(5): 550-555.

[11]TheCaseWesternReserveUniversityBearingDataCenterWebsite.Bearingdatacenterseededfaulttestdata[EB/OL]. [2007-11-27].http: //csegroups.case.edu/bearingdatacenter/pages/download-data-file.

[12]ZhangShuqing,ZhaoYuchun,JiaJian,etal.ResearchontheChaosRecognitionMethodBasedonDifferentialEntropy[J].Chin.Phys.B,2010,19(6):060514.

[13]CrossRecurrencePlotToolboxforMATLAB[EB/OL].[2006-10-24].http://tocsy.agnld.uni-potsdam.de.

(编辑王艳丽)

Fault Diagnosis of Rolling Bearings Based on RQA and GG Clustering

Zhang ShuqingBao HongyanLi PanLi XinxinJiang Wanlu

The Key Lab of Measurement Technology and Instrumentation of Hebei Province,Yanshan University,Qinhuangdao，Hebei,066004

A fault diagnosis method of rolling bearings based on RQA and GG clustering was put forward. The parameters of the RQA which were able to characterize the degree of divergence of the signal-determinism and laminarity were used to consist the fault feature vector. Combined with the GG fuzzy clustering, it could achieve the fault pattern recognition of rolling bearings. The analyses of the actual fault data show that the method is able to identify different degrees of damage of rolling bearing faults and to complete different parts of the bearing fault diagnosis. It provides an efficient and intuitionistic new way for the identification of rolling bearing faults.

fault diagnosis;recurrence plot; recurrence quantification analysis(RQA);GG fuzzy clustering

2013-07-04

国家自然科学基金资助项目(61077071，51475405)；河北省自然科学基金资助项目(F2015203413)

TH17< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.10.019

张淑清(通信作者)，女，1966年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为弱信号检测、机械故障诊断、图像处理与识别等。包红燕，女， 1987年生。燕山大学电气工程学院硕士研究生。李盼，男，1987年生。燕山大学电气工程学院博士研究生。李新新，女，1988年生。燕山大学电气工程学院硕士研究生。姜万录，男，1964年生。燕山大学机械工程学院教授、博士研究生导师。