基于神经网络与遗传算法的关节轴承挤压模具优化

吴连平　杨晓翔

福州大学,福州,350116

基于神经网络与遗传算法的关节轴承挤压模具优化

吴连平杨晓翔

福州大学,福州,350116

针对实际生产中关节轴承内外圈间隙分布不均问题，以GEW12关节轴承为例，应用ABAQUS软件对关节轴承挤压装配过程进行了数值模拟。采用BP神经网络建立了挤压模具形状与内外圈最大间隙与最小间隙之差的映射关系。以关节轴承内外圈间隙均匀分布为目标，结合遗传算法，提出了一种集数值仿真、人工神经网络和遗传算法为一体的关节轴承挤压模具型腔优化设计方法。实验结果表明，模具型腔经过优化后，轴承内外圈间隙均匀性得到了很大的改善，轴承金属流动速度更加均匀。

关节轴承；数值模拟；BP神经网络； 遗传算法

0　引言

关节轴承具有结构紧凑、质量轻、耐冲击、免维护、安全可靠性高和寿命长等优点[1],常用于低速时的摆动运动，也能在一定角度范围内做倾斜运动,能承受较大的载荷。它是工程机械、载重汽车、水利设备、军工机械等领域的重要零件[2]。冷挤压作为关节轴承最重要的成形方式，已有较多学者对其进行了研究。Yang等[3]分析了关节轴承双收口成形相对单边收口成形的优势；Orsolini等[4]用ABAQUS软件分别建立了关节轴承挤压成形的二维轴对称模型和三维模型，得出二者模拟结果差别小于百分之一的结论，并用理论和实验验证了模型的可靠性;Woodhead等[5]用ABAQUS软件对关节轴承一次挤压成形进行了数值模拟，并分析了外圈与模具之间的摩擦因数对挤压力的影响;Wang等[6]利用ANSYS软件对自润滑关节轴承挤压装配过程进行了数值模拟并与实验结果进行了对比。

实际生产的关节轴承常常由于密合度过大而不合格，而挤压模具是冷挤压的关键工艺设备，是技术密集型产品，其设计及制造工作量大，周期长。模具的不合理设计会直接导致轴承密合度过大，因此，以提高内外圈间隙分布的均匀性为目标，对挤压模具进行优化设计是现今轴承行业的研究热点。闫洪等[7]提出了一种集数值仿真、人工神经网络和遗传算法为一体的工艺参数优化模型，合理配置了非对称角铝型材模模孔位置;kahhal等[8]利用遗传算法结合有限元方法对薄板成形模具进行了多目标优化,有效地改善了板料的成形质量;Wu等[9]和Zhao等[10]采用神经网络结合遗传算法对挤压模具进行了优化设计,优化后的模具大大提升了挤压件的成形质量。

本文根据关节轴承挤压装配的特点，采用ABAQUS软件对关节轴承挤压装配过程进行数值模拟，以L16(45)正交试验和6个补充试验作为BP神经网络的训练样本,建立模具圆弧半径R1和R2、轴承收口半径Ra、定径带长度h以及内外圈最大间隙与最小间隙之差δ的非线性映射关系；以内外圈间隙均匀分布为目标，运用遗传算法对模具型腔进行优化。最终得出模具型腔圆弧半径R1、R2,轴承收口半径Ra,定径带长度h等4个参数最佳的组合,结合实验证明了优化结果的可靠性。

1　有限元模型的建立

本文选用GEW12DEM1T轴承进行模拟。轴承外圈材料为0Cr17Ni4Cu4Nb，内圈材料为9Cr18Mo。根据关节轴承实际挤压装配条件，对模具和轴承进行建模。由于挤压过程中轴承几何形状和受力情况都是对称的，所以建立二维轴对称有限元模型进行分析。模具与定位套均采用解析刚体进行求解。每个刚体设置一个参考点，用参考点代表它们的运动。根据模具和轴承的实际尺寸，完成每个零件的几何造型并按照实际工况装配起来，如图1所示。

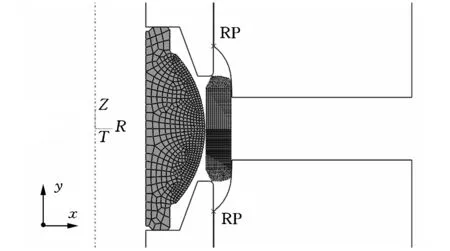
图1　关节轴承的有限元模型

由于关节轴承挤压装配过程属于材料非线性、几何非线性、接触非线性问题，故采用ABAQUS/Expilcit求解器进行挤压分析。根据实际运动关系，本文定义7个接触对。接触面之间的摩擦采用库仑摩擦定律，摩擦因数取为0.15。下模固定，上模和定位套有z方向的进给运动。分析模型的单元尺寸由材料的变形程度确定，因外圈变形较大，对其使用ALE自适应网格划分技术，内圈与外圈有接触的部位网格划分得较细,无接触部分网格划分得较粗。

回弹过程的模拟是基于挤压成形过程的模拟。采用ABAQUS/Standard求解器进行静态隐式分析。将成形过程中的模具和定位套都去除，并对内圈和外圈施加z方向的约束。

2　非线性函数关系的建立

在MATLAB环境下，以模具型腔圆弧半径R1和R2、轴承收口半径Ra、定径带长度h4个参数作为网络的输入量，以内外圈最大间隙与最小间隙之差为网络的输出量,实现BP神经网络的建模。输入层的神经元数取输入参数的个数，输出层神经元数取输出参数的个数。对于各层的激活函数，隐含层采用S形正切激活函数tansig,输出层选用线性激活函数purelin。

2.1BP神经网络训练样本的选择

神经网络的仿真可信度与选择的样本关系较大，因此在选择网络的训练样本时，应尽可能全局反映各参数的变化规律[11]。图2给出了挤压模具结构要素图，由图2可以看出，模具圆弧型腔由半径R1、R2、Ra和定径带长度h决定。其中，模具型腔的圆弧部分主要由半径为R1的圆弧和半径为R2的圆弧组成，为了保证外圈能逐渐缓慢地变形，半径为R2的圆弧的弧度应小于半径为R1的圆弧的弧度。此外，为保证模具型腔的两段圆弧光滑过渡，以R1为半径的圆应内切于以R2为半径的圆，所以半径R2的值也远大于R1的值。表1为四个工艺参数的变化范围，表1中定径带长度和收口半径的大小分别根据外圈的高度和厚度进行取值，半径R2的大小主要根据外圈的外径进行取值，最后根据半径R2、Ra、定径带长度h的值，并在保证以R1为半径的圆应内切于以R2为半径的圆的前提下，获得半径R1的取值范围。在该范围内，采用L16(45)正交试验组成16组试验，并在表1中再随机选取6个补充试验，共22组试验数据为网络的训练样本。针对各参数组合通过采用弹塑性有限元法来获得内外圈最大间隙与最小间隙之差δ,从而组成一个训练样本,如表2所示。

图2　挤压模具结构要素图

试验因素试验水平1234定径带长度h(mm)5.86.16.46.7模具半径R1(mm)3.64.45.26.0模具半径R2(mm)17213054收口半径Ra(mm)13.513.914.314.8

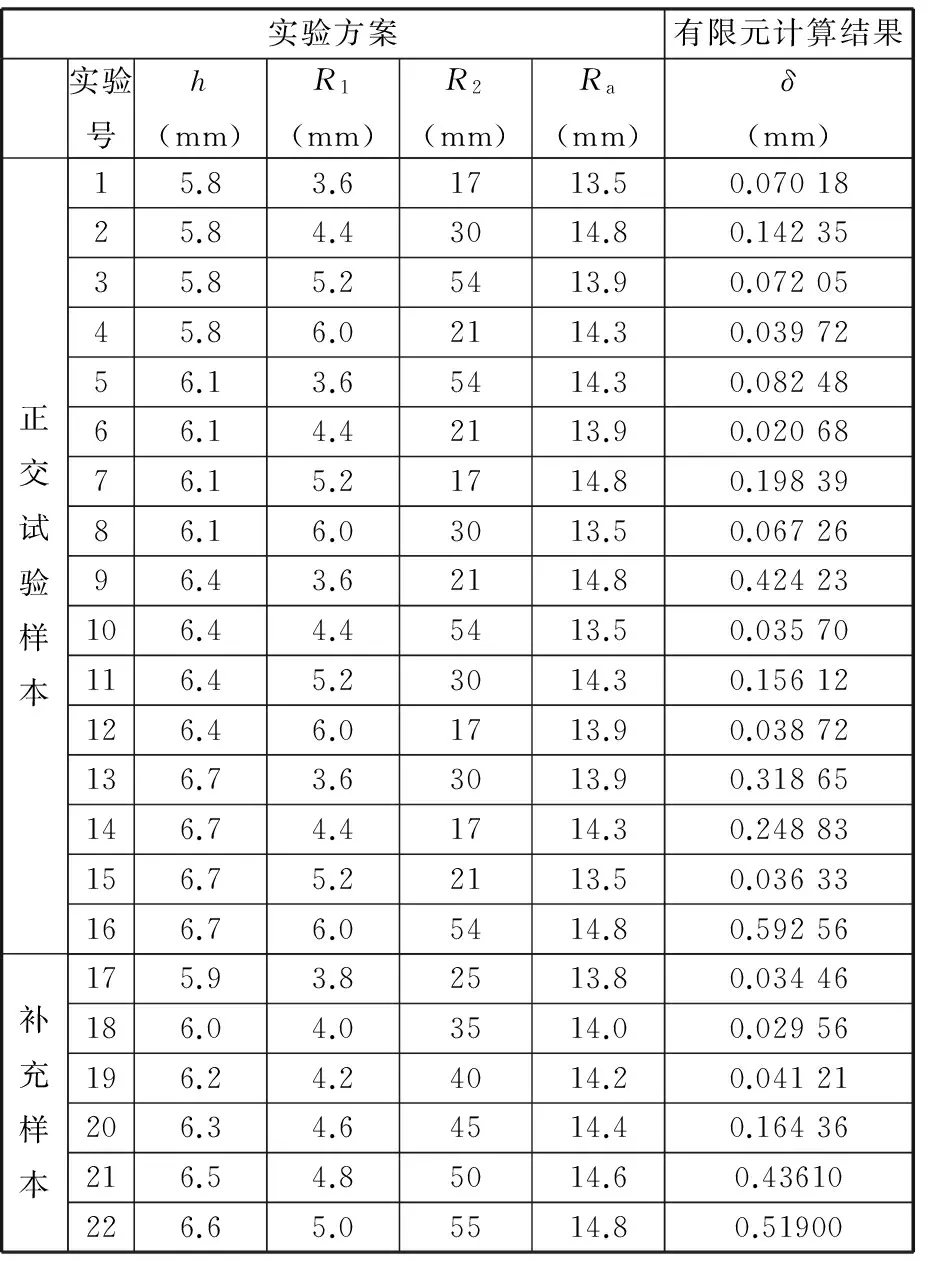
表2　神经网络训练样本

2.2BP神经网络的构建

根据文献[12],至少具有一个S形隐含层加上一个线性输出层的网络,能够逼近任何有理函数。因而本文实验在满足训练要求的前提下，采用三层前馈网络，结构参数如下:输入层神经元个数4个,隐含层神经元个数10个,输出层神经元个数1个。其中隐含层神经元数是在经验公式M=2N+1的基础上,再适当增加1～2个余量。其中，M为隐含层神经元个数，N为输入层神经元个数。

2.2.1样本的归一化处理

由表2给出的训练样本可知,当样本中输入数据的数值差距很大时,输入样本就构成了奇异矩阵，这影响网络的收敛性能及网络精度。因此本次实验调用了mapminmax函数，对输入向量和目标向量进行归一化处理。

2.2.2附加动量法的采用

为了防止BP算法所求的解不是误差平面的全局最小解[13],本文采用附加动量法对网络进行训练。网络训练过程中，训练误差先落入局部极小值，在附加动量的作用下，训练误差能继续向前产生一个正向斜率的运动，跳出峰值，落入全局最小值。

2.2.3自适应学习速率的采用

根据文献[14],BP网络所采用的速率一般凭经验或采用试验的方法选取。这种固定的学习速率不能确保BP网络训练的准确性。本文采用自适应的学习速率，既能加快网络的收敛速度，又能得到较为稳定的神经网络，大大缩短了训练时间。在MATLAB环境下，可以调用traingdx.m把附加动量法和自适应学习速率结合运用。

2.3BP网络的训练过程

图3给出了网络预测值与有限元计算值的比较，由图3可以看出，函数关系曲线较好地拟合了22组输入样本向量和输出样本向量。由此可知，此时的BP网络基本上建立了输入参数与输出参数良好的映射模型。图4给出了网络预测值与有限元计算值之间的误差百分比。由图4可以看出，两者误差很小，最大误差也小于5%。由此说明，训练结束后网络具有较好的推广性，可以作为后续优化模型的知识源。

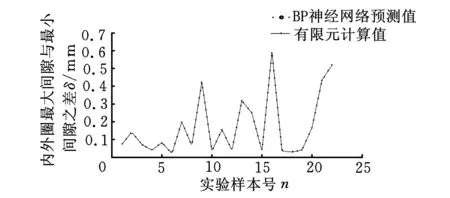
图3　网络预测值与有限元计算值的比较

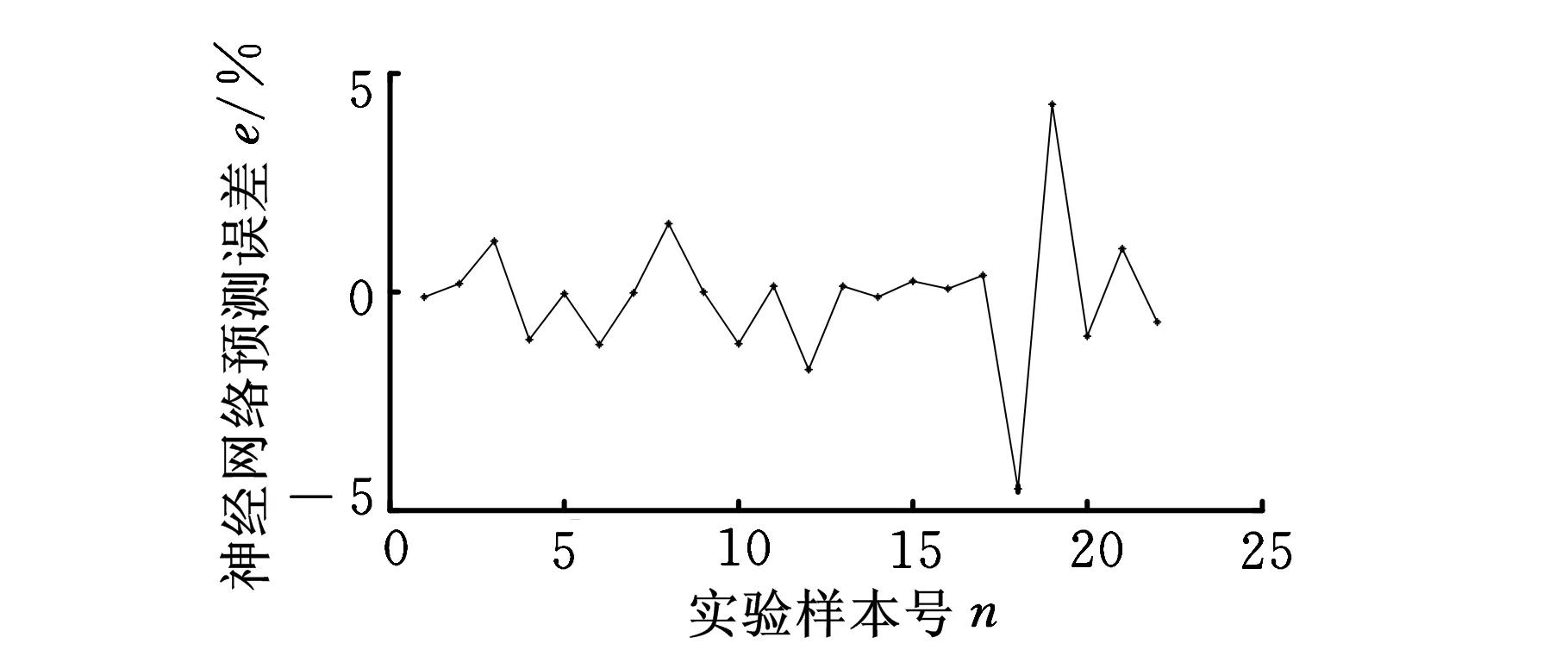
图4　网络预测值与有限元计算值之间的误差

3　工艺参数的优化

3.1遗传算法程序的构建

为了避免搜索过程中产生欺骗性结果或不能有效定位全局的最小值，程序采用格雷码编码。变量取值范围与各个工艺参数的取值范围一致。初始种群采用crtbp创建，随后产生一个矩阵Chorm，它由50个均匀分布长度为50×30的格雷码构成。选用BP神经网络训练构建出良好的输入输出映射关系作为目标函数。适应度函数选择基于排序的适应度函数ranking分配计算。交叉概率为0.4,变异概率为0.2,如果变量是浮点变量,则长度为1。

3.2遗传算法优化过程

图5为采用遗传算法对目标函数进行优化后,目标函数值迭代次数变化的性能跟踪图。经过250次迭代后，目标函数的最优适应度和平均适应度就基本趋于平稳，且目标函数最小值为0,所对应的最优解组合为h=6.1074 mm,R1=4.6132 mm,R2=29.6502 mm,Ra=14.1077 mm。

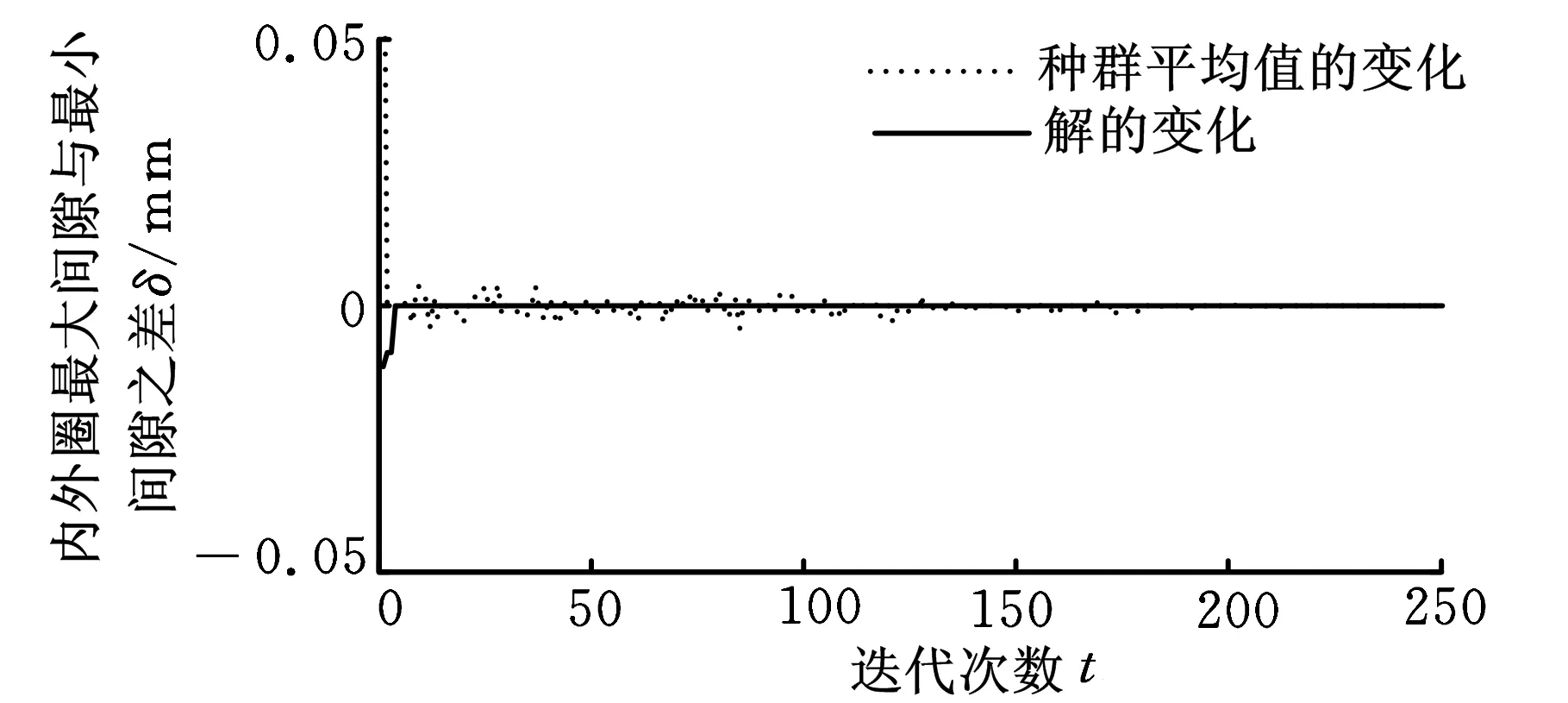
图5　目标函数的变化过程

4　实验验证

4.1FEM模拟验证

为验证GA寻优的真伪，采用FEM对该组实验参数组合进行数值模拟,将其所得到结果与GA的最优解作对比,其结果如表3所示。由表3可知，两者的误差相差较小，仅为0.018 mm,说明GA寻优获得的结果是真实可靠的。

表3　GA优化结果和FEM模拟结果对比　mm

从金属流速角度分析优化后的结果，在挤压成形过程中，外圈表面速度是否均匀，直接影响轴承外圈表面的质量。为了准确地描述轴承外圈表面的速度均匀程度，本文引入轴承外圈表面金属流速均方差Fsdv,其表达式为[15]

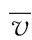
显然,速度均方差越小,轴承表面速度分布越均匀。本文选取轴承外圈表面所有节点并记录其速度值以准确地计算轴承外圈表面速度均方差值。

图6为优化前轴承截面的金属流速分布图，图7为优化后轴承截面的金属流速分布图。由图6、图7可以看出，优化前最大速度为93.51 mm/s,最小速度为22.62 mm/s,轴承外圈表面速度均方差为0.73 mm/s;优化后最大速度为84.80 mm/s,最小速度为28.23 mm/s,轴承外圈表面速度均方差为0.06 mm/s。由此说明通过GA优化模具型腔后，不仅内外圈间隙分布均匀性增加，轴承表面质量也明显提高了。

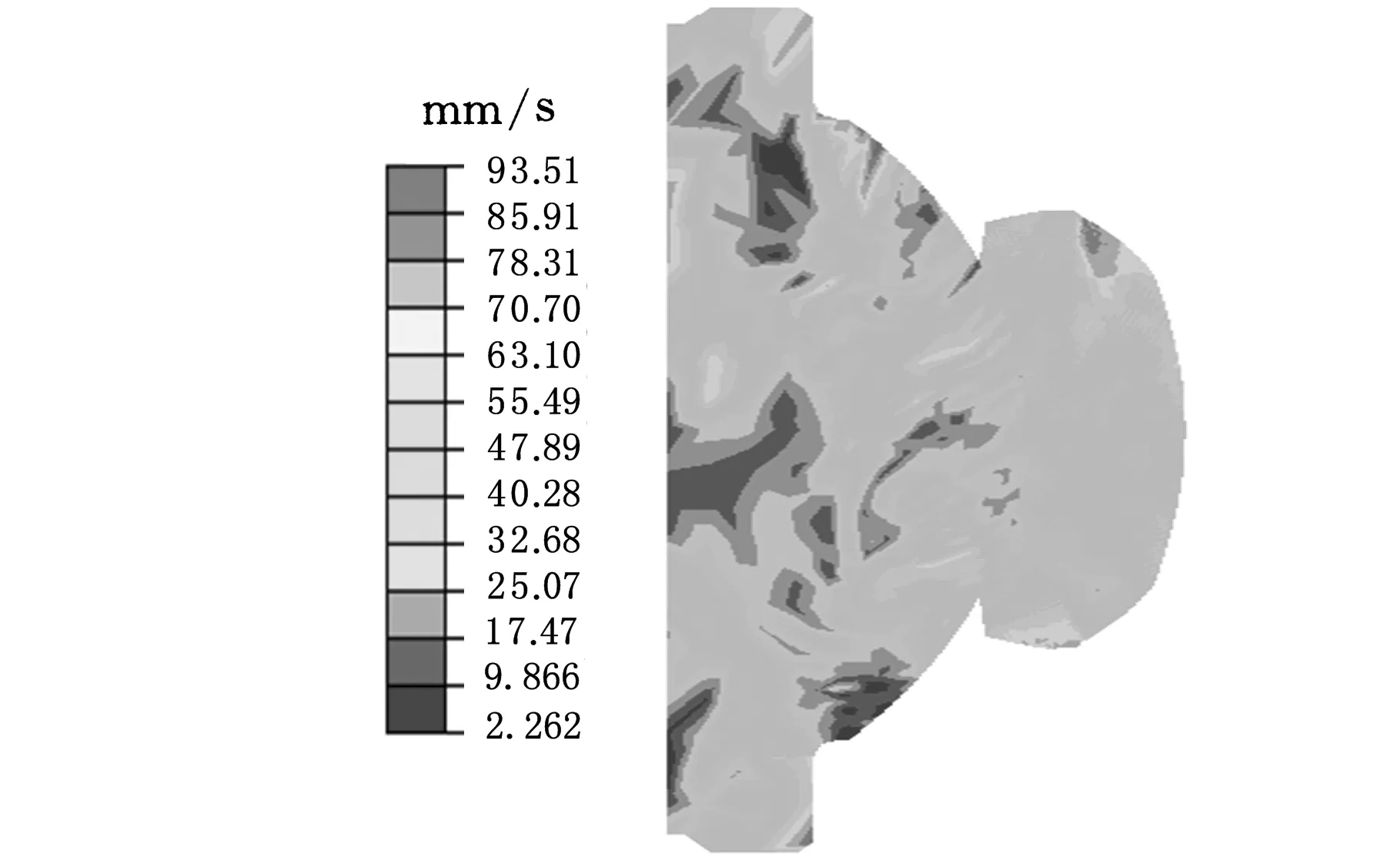
图6　优化前轴承截面的金属流速分布

图7　优化后轴承截面的金属流速分布

4.2物理实验验证

为了验证优化模具的实用性，用经GA寻优后的挤压模具参数组合在100 t的挤压机上对轴承进行挤压装配。图8为挤压获得的关节轴承，其表面质量好，无褶皱、屈曲等缺陷。为测量关节轴承内外圈之间间隙，将关节轴承固化后剖开，如图9所示。再用万能工具显微镜测量内外圈之间的间隙，实验测得最大间隙与最小间隙之差为0.0212 mm,与优化前最大间隙与最小间隙之差0.0442 mm相比得到了大幅度的减小。

图8　关节轴承实物图

图9　剖开后的关节轴承实物图

5　结论

(1)利用ABAQUS软件对关节轴承挤压装配过程进行了数值模拟，并分析了挤压模具的关键参数。

(2)基于虚拟正交试验获得了BP神经网络训练样本，利用BP神经网络建立了挤压模具型腔参数与关节轴承内外圈最大间隙与最小间隙之差的映射关系。

(3)利用遗传算法对映射关系进行优化，获得了最优挤压模具参数组合，并用实验验证优化结果的可靠性。

[1]Chul K B,Chang P D,Sung K H.Development of Composite Spherical Bearing[J].Composite Structures,2006,75(1):231-240.

[2]陈继刚，杨育林，夏振伟,等.整体型外圈关节轴承成形技术现状及发展趋势[J].轴承，2013(9)：58-62.

Chen Jigang,Yang Yulin,Xia Zhenwei,et al.Current Status and Development Trends of Forming Technology for Spherical Plain Bearing with One Piece Outer Ring[J].Bearing,2013(9):58-62.

[3]Yang Yulin,Huang Shijun.Study on New Forming Process for Spherical Plain Bearing and Optimum of the Necking Force[C]//International Conference on Information Engineering.Beidaihe,2010: 216-219.

[4]Orsolini A,Booker J D.Modelling Capabilities Required for the Double Nosing Process in the Assembly of Spherical Plain Bearings[J]. Journal of Engineering Manufacture,2012,226(5):930-940.

[5]Woodhead J,Booker J.Modelling of Nosing for Assembly of Aerospace Bearings[J].Experimental and Applied Mechanics,2013,38:327-338.

[6]Wang Xiumei,Lü Shaowei.Numerical Investigation

on Press Forming of Self-lubricating Spherical Plain Bearings[J].Int. J. Materials and Product Technology,2013,47:46-62.

[7]闫洪,夏巨谌,胡国安.型材挤压过程工艺参数优化模型[J].机械工程学报,2002,38(10):78-81.

Yan Hong,Xia Juchen,Hu Guoan.Optimization of Technological Parameters for Profile Extrusion Process[J].Chinese Journal of Mechanical Engineering,2002,38(10):78-81.

[8]Kahhal P,Brooghani A,Azodi D.Multi-objective Optimization of Sheet Metal Forming Die Using Genetic Algorithm Coupled with RSM and FEA[J].J. Fail. Anal. and Preven, 2013,13:771-778.

[9]Wu C Y,Hsu Y C.Optimal Shape Design of an Extrusion-forging Die Using a Polynomial Network and a Genetic Algorithm[J].International Joural of Advanced Manufacturing Technology,2002,20:128-137.

[10]Zhao Guoqun,Chen Hao,Zhang Cunsheng,et al.Multiobjective Optimization Design of Porthole Extrusion Die Using Pareto-based Genetic Algorithm[J].International Joural of Advanced Manufacturing Technology,2013,69:1547-1556.

[11]周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社，2005.

[12]丛爽.面向MATLAB工具箱的神经网络理论与应用[M].合肥:中国科学技术大学出版社，2009.

[13]杨庆雄.基于神经网络的字符识别研究[J].信息技术,2005(4):92-96.

Yang Qingxiong.Realization of Character Recognition Based on Neural Network[J].Information Technology,2005(4):92-96.

[14]张德丰.MATLAB神经网络应用设计[M].北京：机械工业出版社，2012.

[15]陈浩,赵国群,张存生,等.薄壁空心铝型材挤压过程数值模拟及模具优化[J]. 机械工程学报,2010，46(26):35-39.

Chen Hao,Zhao Guoqun,Zhang Cunsheng,et al.Numerical Simulation of Extrusion Process and Die Structure Optimization for a Hollow Aluminum Profile with Thin Wall[J]. Chinese Journal of Mechanical Engineering,2010，46(26):35-39.

(编辑王艳丽)

Optimization of Extrusion Die of Spherical Plain Bearings Based on BP Neural Network and GA Algorithm

Wu LianpingYang Xiaoxiang

Fuzhou University,Fuzhou,350116

The paper addressed a practical problem of the non-uniform clearance between the outer ring and the inner ring after the nosing process in the assembly of spherical plain bearings,the extrusion process of GEW12 spherical plain bearings was simulated by using ABAQUS software. BP neutral network was applied to identify the relationship between the die profile and the peak difference between the maximum clearance and minimum clearance.A genetic algorithm was used to optimize the die profile,which yielded more uniform clearance distribution. Thus, the FEM, neutral network, and genetic algorithm were combined to develop a method for the design of the optimal shape of a extrusion die.The experimental results show that the clearance distribution between outer ring and inner ring is improved greatly and the metal flow of the bearing becomes more uniform.

spherical plain beating;numerical simulation;BP neural network;genetic algorithm(GA)

2014-06-10

福建省科技重大专项(2012HZ0006-3)

TG375DOI：10.3969/j.issn.1004-132X.2015.10.013

吴连平,女,1988年生。福州大学机械工程及自动化学院硕士研究生。研究方向为金属塑性成形。杨晓翔，男,1963年生。福州大学机械工程及自动化学院教授、博士研究生导师。