基于时变混合Copula的金融市场传染效应研究
2015-10-27徐凯潘攀曹雅晴
徐凯++潘攀++曹雅晴


摘要:针对金融市场普遍存在异方差、波动聚集性、尖峰和厚尾等典型事实,应用GARCH-t模型对边缘分布进行建模,得到“干净”蕴含波动率本源动力学特征的标准残差;考虑到不同市场间存在非对称的传染效应,运用由Gumbel、Frank、Clayton构成的时变混合Copula分析大中华区中国内地、香港、台湾股票市场之间的传染效应,尤其关注代表不同市场同时急剧上涨和急剧下跌的尾部传染关系。实证结果表明,内地股市与香港股市之间表现出与以往研究截然相反的传染特征,即上尾相关性大于其下尾相关性;内地股市与台湾股市之间发生风险传染的可能性不大,但同时也说明应进一步加强两岸之间经济交流与合作;内地与台湾之间呈现出特有的周期性传染关系,其周期时间约为两年。
关键词:金融市场;传染效应;时变混合Copula;尾部相关性
中图分类号:F832.5 文献标识码:A 文章编号:
Research on Contagion Effect of Financial Markets Based on Time-varying Mixed Copula Model
XU Kai1, PAN Pan2, CAO Ya-qing3
(1.School of Economics & Management, Chengdu University, Chengdu 610106;
2.School of Business, Chengdu University of Technology, Chengdu 610059, China; 3.School of Management, Cranfield University, Bedfordshire MK43 0AL, England)
Abstract: In this paper, GARCH-t model is used to capture the stylized facts of financial returns, such as heteroskedasticity, clustering, leptokurtosis and fat tail. And considering the asymmetric character of risk infection, we employed the time-varying mixed Copula model, which combine the Gumbel, Frank and Clayton Copula, to analysis the contagion effects between Hong Kong, Taiwan and China mainland stock markets. The most energy is focus on the tail risk infection, which represents the extreme risk. The empirical results show that, the contagion characters between China mainland stock market and Hong Kong stock market are different from previous studies. That is to say, the upper-tail dependence level is higher than its lower-tail dependence level. The risk contagion effect between Taiwan and China mainland market is slight. It indicates the risk cannot spread from Taiwan stock market to China mainland stock market. There is a cycle risk contagion effect between China mainland and Taiwan stock markets, and the cycle time is about two years.
Key words: financial market; contagion effect; time-varying mixed Copula; tail dependence
引言
在过去的十多年间,全球金融市场爆发了几次重大的金融危机,这些金融危机事件由始发国通过不同渠道传染至其他国家或地区,最终诱发了全球性金融海啸,如2007年美国次贷危机、2009年迪拜危机和希腊债务危机。这表明,金融风险传染广泛存在金融市场之中,并迅速向其他国家或地区蔓延、扩大,最终衍化成全球性金融危机。因此,研究金融市场之间的风险传染对于防范金融危机,对于维护金融市场平稳运行有着极其重要的现实意义。
众所周知,股票市场是一国经济状况的“晴雨表”,如果一个国家的经济发生剧烈波动,将迅速反应在该国股票市场上,并以“多米诺骨牌”方式向其他股票市场传染,造成全球经济动荡。要维护中国金融市场安全与稳定就必须重点监控股市波动,尤其要关注周边股市对中国股市的风险传染特征[1]。香港、台湾地区的金融市场是国际化程度最高的几个市场之一,与中国金融市场有着密切的联系,同时其他国家爆发的金融危机极有可能通过香港、台湾传染至内地股市。近年来,随着自由贸易协议(CEPA)的签署,合格的境外机构投资者(QFII)、合格境内机构投资者(QDII)机制的引入等,使得内地金融市场与香港金融市场之间的金融联系更为紧密。同时,内陆与台湾地区的经济联系上,不仅贸易规模不断扩大,而且贸易依存度急剧上升,特别是随着两岸经济协议(ECFA)的签署等,更是使得内地金融市场与台湾金融市场之间的金融联系进一步加深。因此,研究香港地区、台湾地区与内地股市之间的传染效应对于我国防范金融风险有着重要的意义。
与金融市场发生的小波动相比,急剧上涨或急剧下跌等极端事件将导致投资者的收益巨幅增长或巨幅下降,所以在研究金融市场的风险传染时,学者们通常更加关注于不同金融市场间极端风险传染关系。而收益率的尾部相关系数则表示当收益率发生极端风险时,它对其他金融市场收益率波动的影响程度,即它可以反映一个股票市场的大波动是否会引起其他金融市场的大波动。因此,本文将主要研究内地、香港、台湾股票市场之间的尾部风险传染关系。
目前,已有大量方法被应用于金融风险传染实证研究之中,比较流行的研究方法主要包括相关系数法、以VAR方法为基础的协整、格兰杰因果检验等传统数理统计方法,尽管这些方法取得了较好的实证结果,但这些方法均是从线性视角研究不同金融市场间风险传染关系,因而也就无法对非线性的金融风险传染进行准确描述。相比上述方法,Copula模型不仅能有效解决上述问题,还尤其善于刻画不同金融市场之间的极端风险传染[2]。
Copula函数主要包括对称性的椭圆型Copula函数和非对称的阿基米德Copula函数两种类型,而金融风险传染常常呈现出非对称特征,所以阿基米德Copula函数受到了学者们的普遍青睐。阿基米德Copula函数包括Gumbel-Copula函数,Clayton-Copula函数和Frank-Copula函数。虽然Gumbel-Copula函数能够捕捉上尾相依关系,却无法捕捉下尾相依关系;Clayton-Copula函数能够捕捉下尾相依关系,却难以捕捉到上尾相依关系;而Frank-Copula函数只能刻画对称两尾的相依关系。如果单单使用一种Copula函数,很难准确描述金融市场之间的尾部相依关系。混合Copula函数虽然能够准确地描述金融市场之间非对称的上下尾相依性,但目前的绝大多数实证研究都是假设金融风险传染关系在研究样本范围内保持不变 [3]。事实上,金融市场之间的传染关系更应该被描述为随着外部环境的变化而产生波动 [4-7]。因此,本文在构造由Gumbel,Clayton,Frank构成的混合Copula的基础上,加入时变相关特征,力求对金融市场之间动态的尾部相依关系进行更为准确的描述。
需要指出的是,对金融市场间传染关系研究通常建立在金融收益时间序列上。金融收益时间序列又常常存在尖峰、厚尾、条件异方差等典型事实[8],因此运用Copula模型对金融市场传染分析之前,必须消除上述典型事实对随机变量本身动力学特征的影响。同时考虑到学生t分布相比正态分布能更好拟合厚尾特征,因此本文运用GARCH-t模型对金融收益时间序列进行处理。
综上所述,针对金融市场普遍存在非正态性、尖峰、厚尾和条件异方差等典型事实,应用GARCH-t模型对边缘分布进行建模,得到“干净”蕴含波动率本源动力学特征的标准残差;再运用由Gumbel、Frank、Clayton构成的时变混合Copula分析香港、台湾和内地股票市场之间的传染效应,并着重分析代表不同市场同时急剧上涨和急剧下跌的尾部传染关系。
迄今为止,已有一些国内外相关学者对金融市场之间的尾部相关结构和风险传染效应进行了研究。吴恒煜等使用四种不同Copula对组合信用风险进行了度量 [9];韦艳华、齐树天以内地、香港、日本、泰国等亚洲几个重要的经济体为研究对象,将Copula理论应用于它们之间的风险传染分析之中[2];闫海梅和王波运用三种Copula函数,分别对我国证券市场三种最主要的股票指数之间的尾部相关关系进行了分析[10]。易文德将关注点放在股票指数和日交易量之间的相关关系,结合ARMA、GARCH和Copula模型对尾部进行了分析[11]。虽然以上研究已经取得了较好研究成果,但大多仅仅只是进行了静态研究,并未对金融市场风险传染时变特征展开分析,也较少有文献运用时变混合Copula进行研究,尤其是极少有文献对股市极端风险尾部传染关系进行深入细致分析。
最后,与已有的研究相比,本文的创新性在于:(1)应用由三种不同阿基米德Copula函数组成的混合Copula函数对金融市场间非对称传染结构进行描述,不仅如此,还构建了具有时变特征的时变混合Copula模型,使刻画的金融市场间传染关系更加准确和更加符合实际运行情况;(2)金融市场间同时急剧上涨和急剧下跌会造成经济的剧烈震荡,因此,本文着重分析了代表股票市场之间极端风险传染的尾部相关关系。(3)以大中华区内香港、台湾、内地股票市场为研究对象,对他们之间的尾部风险传染关系进行了深入分析,这对于加强大中华区内区域间经济合作、防范区域间金融风险传染具有极大的参考价值。
1 研究方法
1.1 典型事实约束条件下不同金融市场边缘分布建模方法
由于金融收益序列通常呈现出非正态性、尖峰、厚尾、条件异方差等典型事实特征,它们不仅不能被有效市场理论所解释,而且广泛存在不同金融市场之中。Cont指出,对金融收益进行建模时,将典型事实纳入到研究框架下的波动率动力学特征刻画才是准确、有效的[12]。
由于金融资产收益率的波动具有明显的异方差性,因此,本文使用相比ARCH所需阶数更小的GARCH模型对动态方差进行建模分析。GARCH(p,q)模型如下:
(1)
其中, 为条件方差。
在早期的研究中,金融收益序列的刻画大多以正态分布为基础而展开的。但在实践中,金融收益序列的经验分布常常呈现尖峰、厚尾等特征,如果运用高斯正态分布假设的GARCH模型来刻画金融收益序列的条件边缘分布,势必会出现偏差,得到的实证结果也将值得怀疑。大量实证研究结果表明,与正态分布相比,学生t分布能够更好对金融收益序列的厚尾特征进行刻画。因此,本文采用GARCH-t模型对金融收益序列进行建模,消除尖峰、厚尾等典型事实特征的影响。
1.2 基于典型事实的时变混合Copula函数的构造
Copula相关理论最早由Sklar提出[13]。1959年,Sklar将一个联合分布拆分为n个边缘分布和一个描述边缘分布之间相关结构的Copula函数。运用Copula函数,能够在不考虑单个金融市场边缘分布的情况下,研究各个资产间的相关结构或相关模式,为准确刻画金融市场间传染关系的多元分布函数提供了解决办法。
正如引言中所述,Copula函数主要包括两种类型,椭圆Copula函数族和阿基米德Copula函数族。椭圆Copula函数族包含高斯Copula函数、t-Copula函数,阿基米德Copula函数族包含Gumbel-Copula函数、Clayton-Copula函数和Frank-Copula函数。由于椭圆Copula函数族只能刻画金融市场之间对称的相依关系,而阿基米德Copula函数族既能够刻画金融市场对称又能够刻画不对称的相依关系,因此,这里主要介绍阿基米德Copula函数模型。它们的特点如下:
(1)Gumbel-Copula函数的函数表达式为
(2)
Gumbel函数具有不对称性,且上尾高于下尾,即Gumbel能够刻画金融市场间的上尾相关关系,但较难刻画市场间的下尾相关关系。也就是说,在金融市场急剧上涨的情况下,Gumbel能较好地刻画相关关系,但在急剧下跌的情况下,它不能准确地刻画相关关系。
(2)Clayton-Copula函数的函数表达式为
(3)
Clayton函数也具有不对称性,但其下尾高于上尾,即Clayton能够刻画金融市场间的下尾相关关系,而较难刻画市场间的上尾相关关系,这恰好与Gumbel函数的分布相反。也就是说,在金融市场急剧下跌的情况下,Clayton能较好地刻画相关关系,但在急剧上涨的情况下,它不能准确地刻画相关关系。
(3)Frank-Copula函数的函数表达式为
(4)
Frank函数具有对称性,即Frank能够刻画金融市场间对称的两尾相关关系,但较难刻画市场间的非对称结构。
以上三种阿基米德Copula函数各有优劣,为了更加全面、准确地刻画金融市场间的相关关系,本文运用阿基米德Copula函数中Gumbel-Copula函数、Clayton-Copula函数与Frank-Copula函数组成混合Copula函数,对金融市场间的传染效应进行拟合。混合Copula函数的表达式为:
(5)
其中, 表示Gumbel-Copula函数, 表示Clayton-Copula函数, 表示Frank-Copula函数, 表示三种Copula函数的权重, ,相依性参数 。
金融市场的相依关系并非是静止的,它可能会随着外部经济环境的改变而呈现出不同的状态,因而需要建立动态的Copula函数来刻画金融市场间的相依关系。Patton最早提出了时变Copula函数的概念[14],也就是在Copula函数中引入时间参数。随后,Patton将时变Copula函数概念进一步完善[15],令参数随着时间作动态变化,其函数表达式为:
(6)
其中,函数 是逻辑转换函数,其目的是为了确保相依性参数 一直在(-1,1)区间内。 , 是由原序列进行概率积分变换后得到的标准收益序列。
1.3 金融市场极端风险传染测度方法
金融市场的极端风险(急剧上涨或急剧下跌)发生的概率很小,一旦发生投资者将承担过大的风险,甚至面临灭顶之灾。因此,与股票市场上平时的波动相比,投资者更关注股票市场极端风险的发生。在金融分析中,尾部系数通常用来描述金融市场极端风险发生的概率,因此本文将利用尾部相关系数分析股票市场间的尾部传染关系。
这里引入条件概率 ,它反映了当 时, 的概率,即一种资产价格高涨后,另一种资产价格高涨的概率。
设X,Y为两个随机变量,其分布函数的形式分别为F和G,则X和Y的上尾相关性和下尾相关性可分别定义为: , 。其中 , 。如果 或 存在且 或 ,那么X与Y具有上尾或下尾相关性,如果 或 ,那么X与Y在上或下尾独立。结合尾部相关系数的定义和Copula函数的定义,得到尾部相关系数的Copula表示形式:
(7)
(8)
2 实证分析
2.1 样本选取与说明
本文取恒生指数、台湾50指数、沪深300指数每日的收盘价为样本数据,分别代表香港地区、台湾地区和中国内地股市状况。选取样本时间段为2003年1月1日至2014年5月1日,恒生指数共3537个收盘价数据,台湾50指数共2859个收盘价数据,沪深300指数共2987个收盘价数据。由于三个股票市场的休市日期不同,因此需要对数据作简单的匹配处理。在剔除不匹配数据后,得到2609组收盘价数据样本。
2.2 描述性统计分析
用 表示第t日的收盘价,通过 得到对数收益率,并对收益率进行波动状况分析和描述性统计分析,分析结果如表1所示。从表中可以看出,在样本观察期内,恒生指数,台湾50指数,沪深300指数的收益序列呈现出明显的尖峰厚尾特点,且具有非正态性和异方差性。
2.3 边缘分布参数估计与检验
由于收益率有自相关性、异方差性等典型事实的存在,因此在运用Copula模型对收益序列建模之前,需要运用模型对金融收益序列进行处理,消除上述典型事实的影响,得到标准收益序列。本文运用GARCH-t模型对恒生指数、台湾50指数和沪深300指数收益率分别建模,并对积分转换后的标准残差进行K-S检验。模型的参数估计及检验结果如表2所示。
注:括号内为边缘分布模型参数υ、ω、α、β的p值。
如上表所示,表中K-S统计量值均大于K-S判断值,表明变换后的各收益序列均服从(0,1)的均匀分布。这说明GARCH-t模型的应用,能够充分地刻画以上各序列。
2.4 尾部相关性分析
通过运用GARCH模型对边缘分布进行建模,得到了消除典型事实影响后的标准收益序列。因此,我们可以运用由Gumbel、Frank、Clayton构成的时变混合Copula模型来描述大中华区内香港、台湾、内地股票市场之间的尾部相依关系。
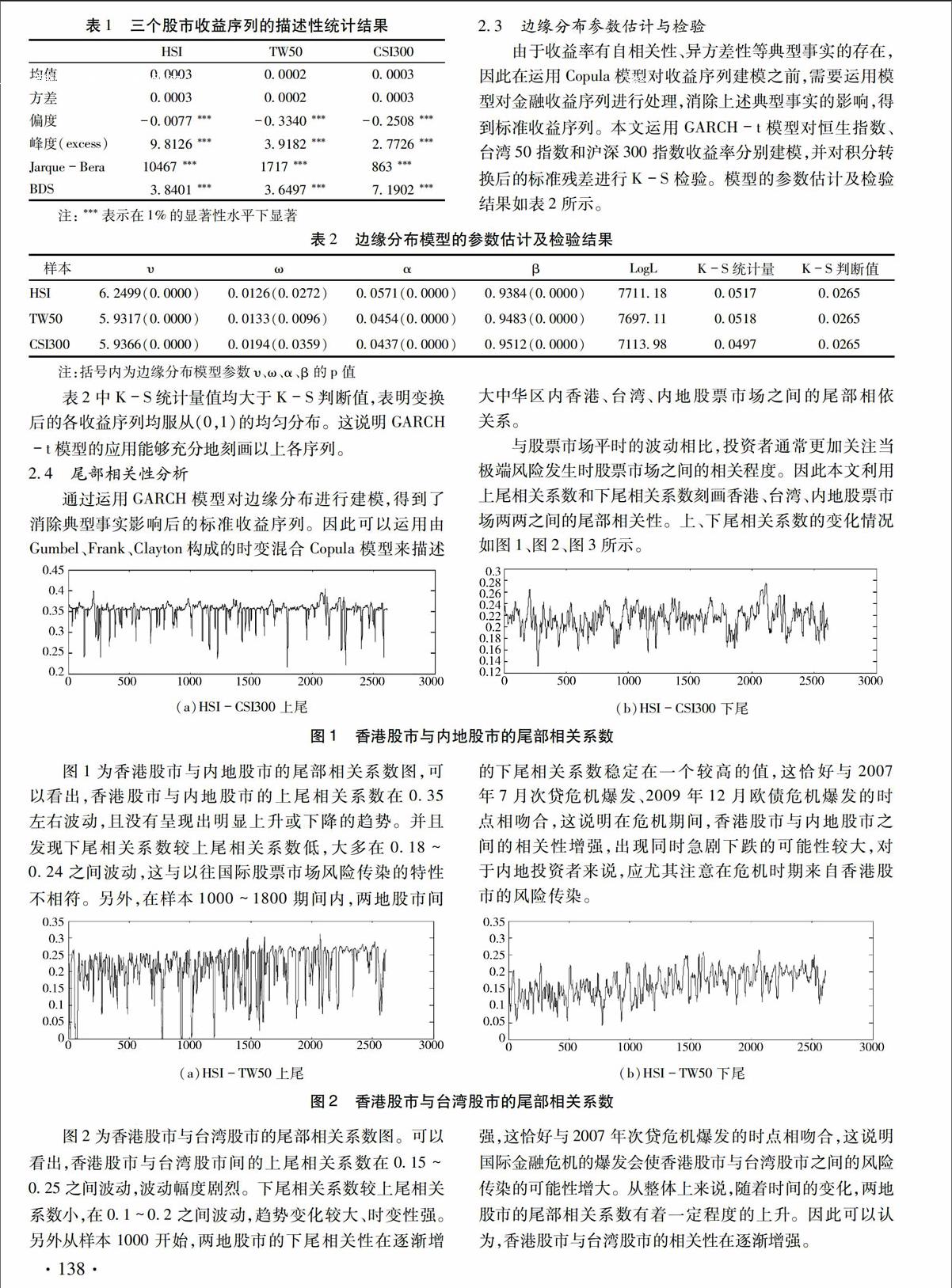
与股票市场平时的波动相比,投资者通常更加关注当极端风险发生时,股票市场之间的相关程度。因此我们利用上尾相关系数和下尾相关系数刻画香港、台湾、内地股票市场两两之间的尾部相关性。上、下尾相关系数的变化情况如图1、图2、图3所示。
(a)HSI-CSI300上尾
(b)HSI-CSI300下尾
图1 香港股市与内地股市的尾部相关系数
图1为香港股市与内地股市的尾部相关系数图,可以看出,香港股市与内地股市的上尾相关系数在0.35左右波动,且没有呈现出明显上升或下降的趋势。我们惊讶发现,下尾相关系数较上尾相关系数低,大多在0.18-0.24之间波动,这与以往国际股票市场风险传染的特性不相符。另外,在样本1000-1800期间内,两地股市间的下尾相关系数稳定在一个较高的值,这恰好与2007年7月次贷危机爆发、2009年12月欧债危机爆发的时点相吻合,这说明在危机期间,香港股市与内地股市之间的相关性增强,出现同时急剧下跌的可能性较大,对于内地投资者来说,应尤其注意在危机时期来自香港股市的风险传染。
(a)HSI-TW50上尾
(b)HSI-TW50下尾
图2 香港股市与台湾股市的尾部相关系数图
图2为香港股市与台湾股市的尾部相关系数图,可以看出,香港股市与台湾股市间的上尾相关系数在0.15到0.25之间波动,波动幅度剧烈。下尾相关系数较上尾相关系数小,在0.1到0.2之间波动,趋势变化较大,时变性强。另外,从样本1000开始,两地股市的下尾相关性在逐渐增强,这恰好与2007年次贷危机爆发的时点相吻合,这说明,国际金融危机的爆发会使香港股市与台湾股市之间的风险传染的可能性增大。从整体上来说,随着时间的变化,两地股市的尾部相关系数有着一定程度的上升。因此,我们可以认为,香港股市与台湾股市的相关性在逐渐增强。
(a)CSI300-TW50上尾
(b)CSI300-TW50下尾
图3 内地股市与台湾股市的尾部相关系数图
图3为内地股市与台湾股市的尾部相关系数图,可以看出,内地股市与台湾股市的上尾相关系数大多在0.06到0.16之间波动,较前两组市场的上尾相关系数小。下尾相关系数与上尾相关系数的数值差异不大,在0.05到0.15之间波动。我们可以认为内地股市与台湾股市的风险联系较弱。
值得注意的是,内地股市与台湾股市的尾部相关性呈现出周期性变化。每隔400个样本,也就是每隔2年左右的时间,两地股市的尾部相关系数会出现一次周期性波动,且上尾相关系数与下尾相关系数的周期性波动大致相同。在样本2003年1月至2014年5月期间内,共发生了7次周期性波动。
从上述分析中我们可以看到,除内地股市与台湾股市之间的上下尾系数基本一致外,另外两个股票市场两两之间的尾部相关结构均呈不对称,其上尾相关性均高于其下尾相关性,这与以往国际股票市场风险传染的特性不相符。原因可能是中国内地股票市场尚处于发展的进程中,资本开放的深度较小,因此利好消息对股市的影响略大于利空消息对股市的影响。
3 结论
本文针对金融市场普遍存在异方差、波动聚集性、尖峰和厚尾等典型事实,应用GARCH-t模型对边缘分布进行建模,得到“干净”蕴含波动率本源动力学特征的标准残差;考虑到不同市场间存在非对称的传染效应,运用由Gumbel、Frank、Clayton构成的时变混合Copula分析大中华区中内地、香港、台湾股票市场之间的传染效应,尤其关注代表不同市场同时急剧上涨和急剧下跌的尾部传染关系。通过实证研究分析,得到以下一些有价值的研究结论:
(1)香港股市与内地股市之间的尾部相关系数较大,尾部相关性强,表明两地股市之间风险传染的可能性较大。但我们惊讶发现,香港股市与内地股市之间的上尾相关性高于下尾相关性,即两地股市同时上涨的概率高于同时下跌的概率,这与国际股票市场风险传染的特性不相符。并且在次贷危机和欧债危机期间,香港股市与内地股市之间的的下尾相关性较大,说明在危机期间,两地股市风险传染的可能性增大,对于内地投资者来说,应尤其注意在危机时期来自香港股市的风险传染。(2)香港股市与台湾股市之间的尾部相关性随着时间的变化,呈现出上涨的趋势,说明两地股市之间风险传染的可能性在逐渐增大。因此在作投资决策时,投资者应注意优化资产配置,调整资产组合中所持香港股票和台湾股票的比例,以达到控制风险的目的。(3)内地股市与台湾股市之间的尾部相关性较小,尽管表明两地股市之间发生金融传染的可能性不大,但也说明内地与台湾之间的经济联系有待于进一步加强,应更大力度推进两岸间经济交流与融合。值得注意的是,内地股市与台湾股市之间的尾部相关性呈现出周期性波动,其波动周期大约两年。这种情况在以前的研究中未曾出现过,值得在以后的研究中进行深入分析原因以及周期特征。
参考文献
[1]杨竹清,刘少波.境外股东持股对中国股市风险的影响研究[J].软科学,2013,27(5):75-79.
[2]韦艳华,齐树天.亚洲新兴市场金融危机传染问题研究—基于Copula理论的检验方法[J].国际金融研究,2008:22-29.
[3]Muns S.Measuring and Explaining Systemic Risk with Stock Prices[R].Working Paper, Erasmus University Rotterdam,2011.
[4]Bartram S, Taylor S, Wang Y. The Euro and European Financial Market Dependence[J].Journal of Banking&Finance,2007,31(5):1461-1481.
[5]Rodriguez J C. Measuring Financial Contagion: A Copula Approach[J].Journal of Empirical Finance,2007,14(3):401-423.
[6]Hafner C M, Manner H. Dynamic Stochastic Copula Models: Estimation, Inference and Applications[J]. Journal of Applied Econometrics,2012,27(2):269-295.
[7]王永巧,刘诗文. 基于时变Copula的金融开放与风险传染[J].系统工程理论与实践,2011,31(4):778-784.
[8]林宇.典型事实—极值理论与金融市场动态风险测度研究[J].投资研究.2012:41-56.
[9]吴恒煜,李冰,严武.投资组合信用风险的测度和优化——基于Copula理论 [J].软科学,2010,24(10):128-133.
[10]闫海梅,王波.沪深300指数与沪深股市尾部相关性分析[J].数学的实践与认识,2010,40(22):50-55.
[11]易文德.基于ARMA-GARCH-COPULA模型的交易量与股价波动相依关系[J].系统管理学报.2012,21(5):696-703.
[12]Cont. Empirical properties of assets returns: Stylized facts and statistical issues[J]. Quantitative Finance, 2001,(1):223-236.
[13]Sklar, A. Fonctions de repartition à n dimensions et leurs marges [J]. Publ. Inst. Statistique Univ. Paris, 1959, 8: 229-231.
[14]Patton A J. Modeling time-varying exchange rate dependence using the conditional copula[Z]. Department of Economics, University of California, San Diego,2001.
[15]Patton A J.Modeling Asymmetric Exchange Rate Dependence[J].International Economic Review.2006.47(2):527-556.
