深水锚在海床中复杂动力行为的分析模型

宋海娟，刘海笑，赵燕兵

(天津大学 建筑工程学院，天津 300072)

深水锚在海床中复杂动力行为的分析模型

宋海娟，刘海笑，赵燕兵

(天津大学 建筑工程学院，天津 300072)

深水锚是深水系泊系统的核心组成，随着新概念和新技术在深水系泊领域的不断涌现和发展，深水锚在海床中的动力行为变得更为复杂，这给既有的分析方法带来极大的挑战。将深水锚的复杂动力行为视为拔出、旋转、嵌入三种典型行为的组合，分别给出明确定义并建立力学模型。提出最小力准则以确定锚的拔出、嵌入方向和旋转中心，该准则同时可作为拔出、旋转、嵌入行为是否发生的判定条件，从而建立起可以描述深水锚在海床中复杂动力行为的分析模型。为检验所提出的分析模型，将其应用于预测拖曳锚在海床中的嵌入运动轨迹，并与已有分析方法和离心机试验结果进行对比，验证了该分析模型的有效性。

深水锚；动力行为；分析模型；运动轨迹；海床

随着国际海洋油气开发迈入深水和超深水，大型浮式海洋平台及适用于深水油气开发的绷紧式系泊方式得到了日趋广泛的应用，同时也对深水系泊系统的安装稳定性和系泊性能提出了更高的要求。深水锚是深水系泊系统的核心组成部分，工程中常见的深水锚类型有吸力锚、拖曳锚、吸力嵌入式板锚和重力贯入锚，如图1所示。由于迥然各异的结构特性和安装方式，不同类型的深水锚在海床中的动力行为复杂且各具特点，如吸力锚在负压作用下的定点沉贯，拖曳锚在海床中长距离的拖曳安装，吸力嵌入式板锚在负压定点贯入后的旋转，以及重力贯入锚在自重作用下的初始贯入和在海床中后续的旋转和嵌入。深水锚在海床中的这些复杂动力行为，不断更新人们的既有认知，挑战人们的分析能力。

深水锚在海床中所体现的复杂动力行为，一方面是其安装技术的需要，以拖曳锚的安装过程为例，拖曳锚抛锚至海床面后，基于锚板自身结构与海床面形成一定的初始角度，通过拖船缓慢的水平移动，锚板逐渐下嵌至目标深度，同时锚板与水平面的夹角，即方位角，也发生变化，如图2所示；另一方面体现在系泊状态尤其在极端环境下能保证更大的承载力。以重力贯入锚为例，2008年在墨西哥湾的现场测试发现[1]，在经历一场大风暴后，组成系泊系统的8枚初始贯入深度为15.2～18.3 m的重力贯入锚，不仅没有随大幅漂移的平台被拔出，相反在7根系缆先后断裂的情况下，出人意料地在海床中均不同程度地达到了更大埋深(19.2～36.6 m)，从而有效化解了在极端环境下因平台系泊系统受损导致的次生灾害。重力贯入锚这种可抵御灾害条件的优异性能，正是由于其在极端载荷条件下具有复杂的动力行为。可以说，深水锚在海床中的复杂动力行为不仅与其安装技术和系泊性能密切相关，更是大型浮式海洋平台在极端载荷条件下重要的安全保障。

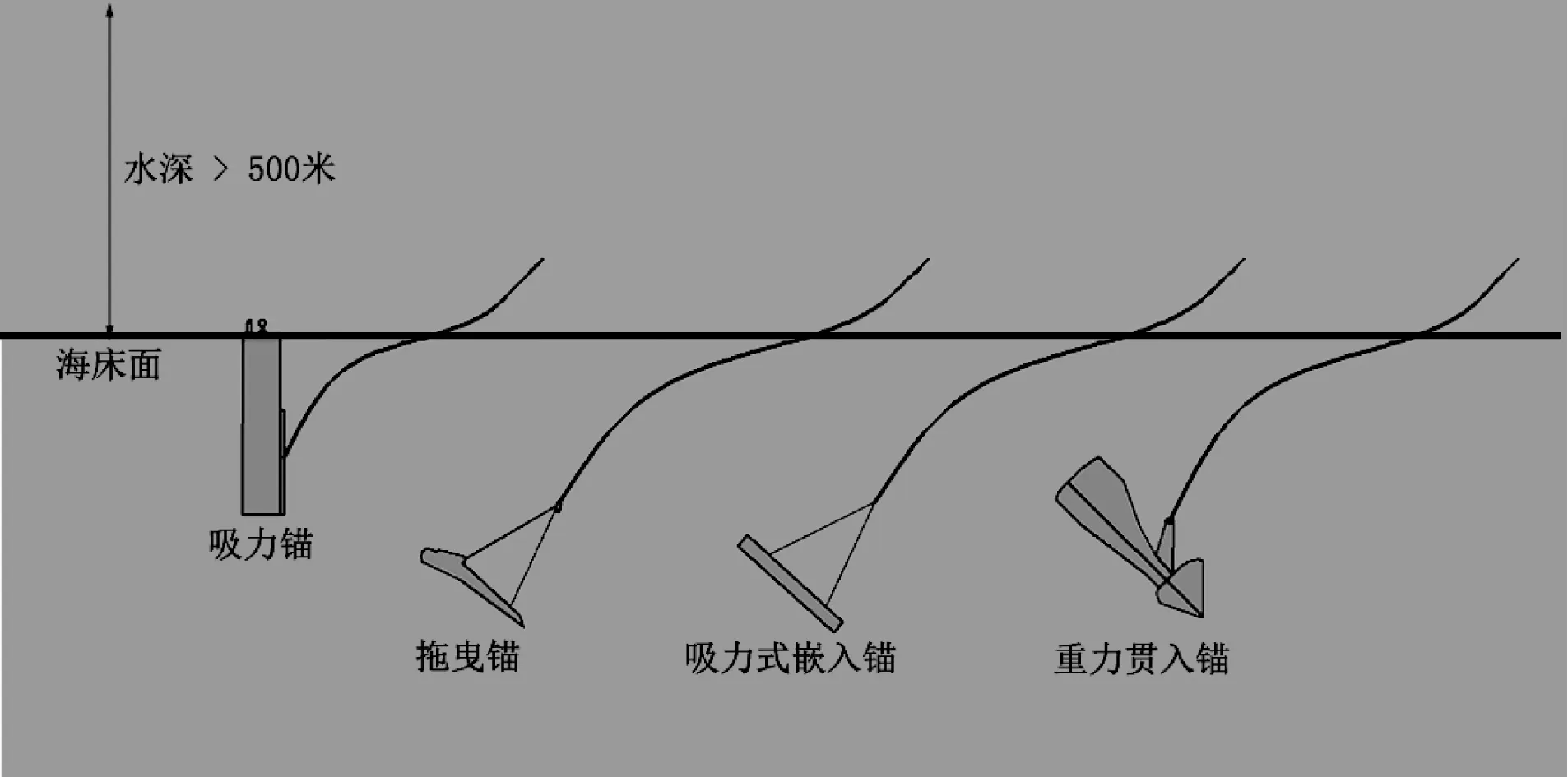
图1 典型深水锚示意Fig. 1 Schematic of typical deepwater anchors

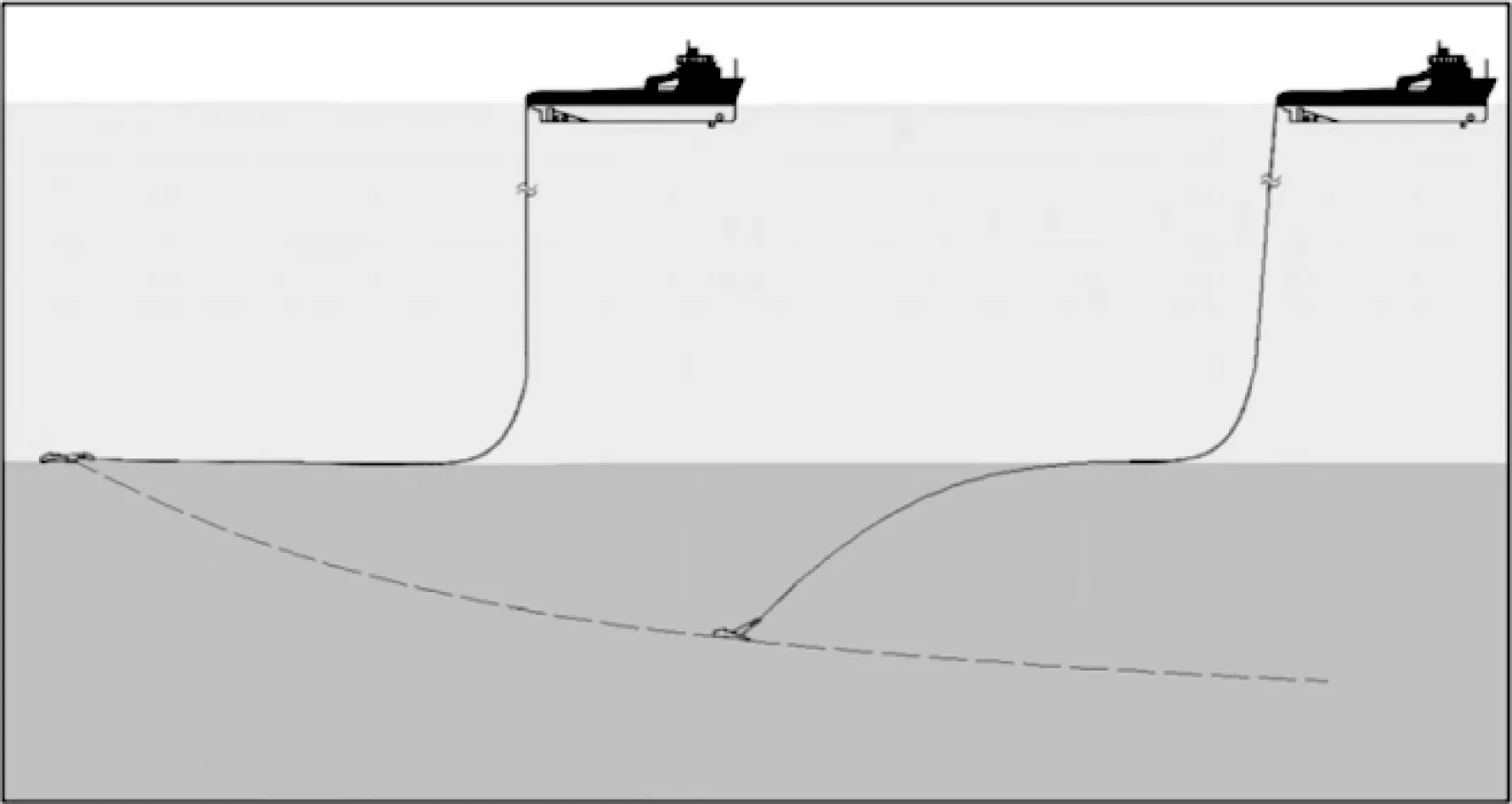
图2 拖曳锚安装过程示意Fig. 2 Schematic of the drag anchor installation process

从物理学角度分析，深水锚的上述复杂动力行为可以描述为其深度和方位角的变化，在理论分析时均可看作拔出、旋转和嵌入三种行为共同作用的结果。例如，在研究拖曳锚的运动轨迹时，通常将其视为嵌入和旋转行为的组合[2-5]。对于拖曳锚的嵌入行为，研究者们通常假设锚沿板面行进[2-5]。对于拖曳锚的旋转行为，目前有两种典型处理方式：一种是假设在锚的整个嵌入过程中拖曳力与锚板夹角，即拖曳角，为一特征常数(如等于锚胫角)，当拖曳角大于该特征常数时，锚发生旋转[3]；另一种是对锚建立力矩平衡方程，当不满足力矩平衡时，锚发生旋转[2,4-5]。在研究吸力嵌入式板锚在负压定点贯入后的埋深损失时，通常将其视为旋转和拔出的组合，目前仅有的理论分析方法为Cassidy等[6]基于塑性上限法开展的研究，但其屈服函数中的参数取值存在较大的不确定性。对于重力贯入锚在安装过程中和工作状态下的旋转、拔出和嵌入行为，国内外尚未有相关的理论研究成果。

综上所述，深水锚在海床中的动力行为变得更为复杂，这给既有的分析方法带来极大的挑战。一方面，对深水锚在海床中复杂动力行为的发生机理缺乏认识；另一方面，难以提出一套能够准确描述不同类型的深水锚在任意载荷条件下综合行为的力学模型。

首先将深水锚的综合行为分解，基于实际物理情况，明确定义了锚在海床中的拔出、旋转和嵌入行为；其次，基于承载力分析理论和极限平衡法，建立了描述深水锚拔出、旋转和嵌入行为的力学模型；提出了最小力准则以确定锚的拔出、嵌入方向和旋转中心，该准则同时可作为拔出、旋转、嵌入行为是否发生的判定条件，从而建立起可以描述深水锚在海床中综合行为的分析模型。值得注意的是，文中所提出的分析模型在确定深水锚的拔出、嵌入方向和旋转中心以及判断拔出、旋转和嵌入行为是否发生时，并非事先假设，而是基于符合物理实际的力学模型及“最小力准则”直接求解，具有明确的理论依据和判定准则。为检验本文所提出的分析模型，将其应用于拖曳锚的嵌入运动轨迹预测，并与已有分析方法和离心机试验结果进行了对比。

1 力学模型

深水锚的复杂动力行为可描述为其深度和方位角的变化，因此，在理论分析时，可将其分解为拔出、旋转和嵌入行为的叠加。本节首先对锚的拔出、旋转和嵌入行为作出严格定义；为确保深水锚的安装稳定性，工程实际中其安装速度通常极小，锚近似处于极限平衡状态，因此，可基于承载力分析理论和极限平衡法[2-4]，建立深水锚在海床中拔出、旋转和嵌入行为的力学模型。此外，文中还引入缆绳方程，以考虑缆绳对深水锚复杂动力行为的影响。

不同类型的深水锚几何形状各异，但均具有典型的结构特性，即由锚板和锚胫组成。本文所提出的理论分析模型均基于该典型结构形式，如图3所示。

1.1拔出、旋转和嵌入行为的定义

深水锚拔出、旋转和嵌入行为的定义如图3所示。其中，Ta表示系缆点处的拖曳力；θm为锚运动方向与锚板上表面的夹角，以顺时针方向为正，逆时针方向为负，当锚沿锚板上表面嵌入时，θm=0°。所谓拔出即锚的运动方向在海床面以上，数学上表达为-π-θ0≤θm<-θ0，见图3(a)，其中θ0表示锚板方位角，即锚板与水平面的夹角。所谓旋转即锚绕某一固定点转动，该点定义为旋转中心，用Pk表示，见图3(b)。Lb表示锚胫与锚板中轴线的交点到锚尾端中心点的距离；Lk表示旋转中心到锚尾端中心点的距离；Lc表示拖曳力与锚板中轴线的交点到锚尾端中心点的距离。假设旋转中心位于锚板中轴线上，以获得最大的旋转效率。对拖曳锚而言，由于其在整个嵌入运动过程中均为逆时针转动，因此，旋转中心只能位于锚尾端中心点和拖曳力与锚板中轴线交点之间，数学上表达为0≤Lk≤Lc。在定义上，嵌入与拔出行为的区别仅在于运动方向不同，所谓嵌入即锚的运动方向在海床面以下，数学上表达为-θ0≤θm<π-θ0，见图3(c)。

图3 拔出、旋转和嵌入行为的定义Fig. 3 Definitions of pulling out, keying and diving

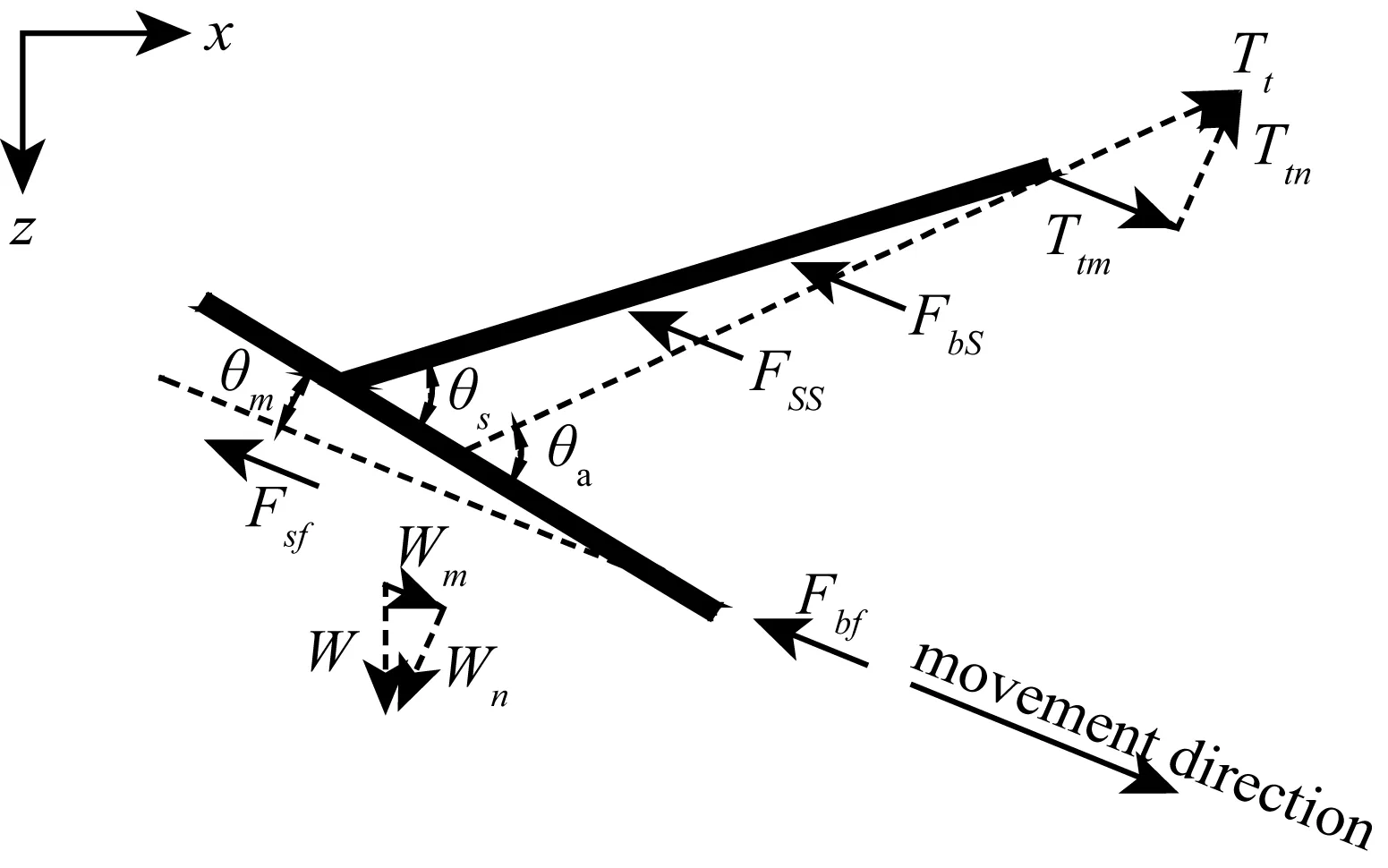
图4 深水锚的拔出、嵌入力学模型Fig. 4 Mechanical model of the deepwater anchor under pulling out or diving

1.2拔出、嵌入行为的力学表达

由1.1节可知，拔出、嵌入行为在定义上的区别仅在于运动方向不同。典型深水锚在拔出、嵌入状态下的受力模型如图4所示。其中，Tt表示发生拔出或嵌入时系缆点处的拖曳力，若对应拔出，Tt为拔出拖曳力Tp；若对应嵌入，则Tt为嵌入拖曳力Td。Ttm和Ttn分别表示Tt沿运动方向和垂直于运动方向的分量。θa为拖曳力与锚板上表面的夹角；θs为锚胫角；W为锚的浮容重，Wm和Wn分别表示W沿运动方向和垂直于运动方向的分量；Fbf为锚板所受端阻力，Fbs为锚胫所受端阻力；Fsf为锚板所受摩阻力，Fss为锚胫所受摩阻力。为简化表达，定义Fb和Fs，分别表示沿深水锚运动方向总的端阻力和摩阻力，其中Fb=Fbf+Fbs，Fs=Fsf+Fss。

沿锚板运动方向建立受力平衡方程：

由图4所示的几何关系，可获得锚发生拔出、嵌入行为时的拖曳力：

饱和黏土中，借用Skempton[7]条形基础承载力公式，可得到锚所受端阻力Fb的表达式：

其中，Ncf为锚的端阻力系数，Ab为锚的有效端阻面积，即锚在垂直于运动方向平面上总的投影面积，包括锚板和锚胫。饱和黏土可视为无摩擦材料，其不排水抗剪强度su可表示为su=su0+kz，其中，z为海床面以下的深度，su0为海床面(z=0)的土体不排水抗剪强度，k为土体不排水抗剪强度梯度。

摩阻力由土的黏滞性产生，借用摩阻力计算公式，可得到锚所受摩阻力Fs的表达式：

其中，α为土的黏滞系数，As为锚的有效摩阻面积。

因此，作用于锚的总端阻力和总摩阻力可以表示为：

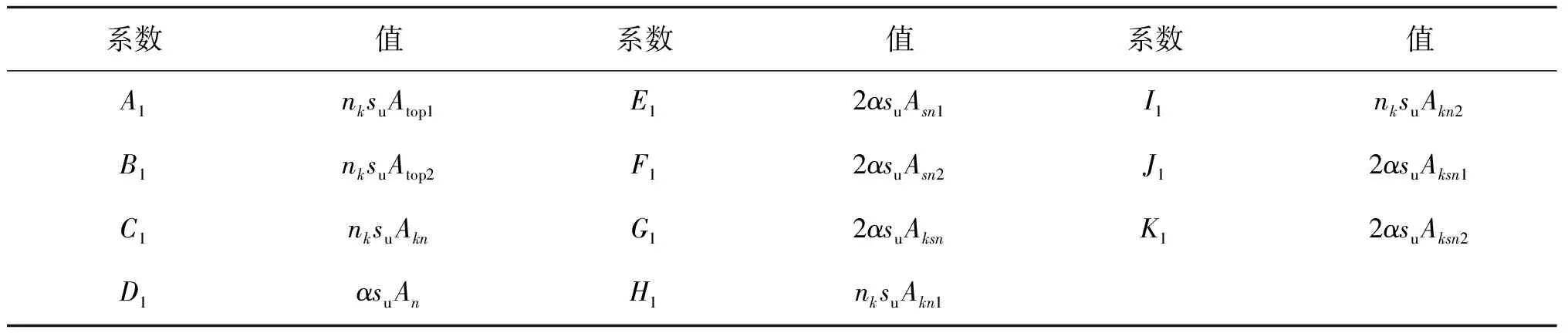
其中，A～G为包含锚、土特性的系数，均为正值，如表1所示。其中涉及的深水锚特性参数见表2。图6以典型深水锚为例，给出其面积参数的具体位置。而对于工程实际中形状不规则的深水锚，应根据表2中的参数含义进行面积参数的取值。

表1 方程(5)中所涉及系数Tab. 1 Coefficients in Eq. 5

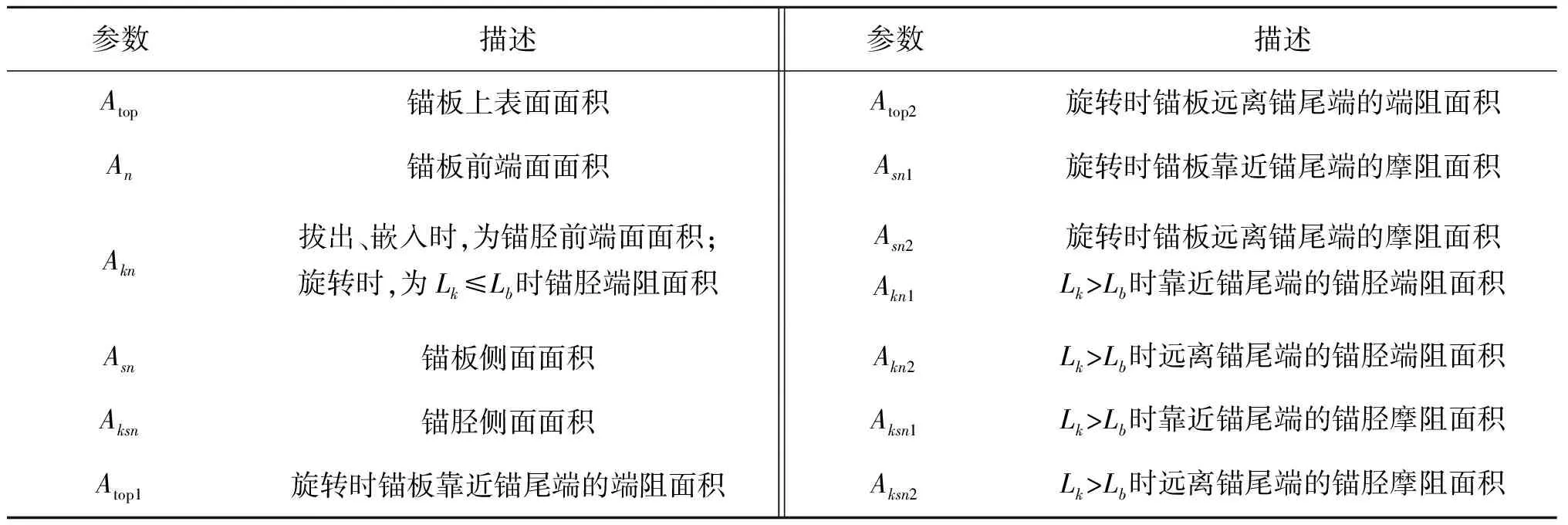
表2 深水锚特性参数表Tab. 2 Parameters of deep water anchors

图5 深水锚的旋转力学模型Fig. 5 Mechanical model of the deepwater anchor under keying

1.3旋转行为的力学表达

深水锚在旋转状态下的受力模型如图5所示。其中，Tk表示发生旋转行为时系缆点处的拖曳力，Tkm和Tkn分别表示Tk沿锚板上表面和垂直于锚板上表面的分量。同样，为简化表达，定义Mb和Ms，分别代表旋转时作用于锚的总的端阻力矩和摩阻力矩。

对锚建立力矩平衡方程：

其中，Lw为重心到锚尾端中心点的距离。

由图5所示的几何关系，可获得锚发生旋转行为时的拖曳力：

深水锚在海床中运动时，Lk与Lb的相对大小并不固定，若Lk≤Lb，作用于锚的总的端阻力矩和摩阻力矩可表示为：

其中，Lf为锚板长度，L0为锚胫中轴线的长度,A1～G1为包含锚、土特性的系数，均为正值，如表3所示。其中涉及的深水锚特性参数见表2。

若Lk>Lb，作用于锚的总的端阻力矩和摩阻力矩可表示为：

其中，A1～K1为包含锚、土特性的系数，均为正值，如表3所示。其中，nk为旋转土抗力系数，是深水锚的旋转行为所涉及的重要参数。运用有限元软件ABAQUS计算了旋转中心在锚板中轴线中点、端点两种情况下的破坏模式。基于该破坏模式，通过塑性上限法求得了上述两特定点的旋转土抗力系数nk，并拟合得到了旋转中心在锚板中轴线范围内的nk。经验证，当nk为二次函数时，相互作用曲线外凸，且与O’Neill等[8]的有限元结果吻合较好。计算得旋转土抗力系数nk=6+28(Lk-Lf/2)2/Lf2。表3中其余的深水锚特性参数见表2。

图6 表2中参数图示Fig. 6 Schematic of the parameters in Table 2

系数值系数值系数值A1nksuAtop1E12αsuAsn1I1nksuAkn2B1nksuAtop2F12αsuAsn2J12αsuAksn1C1nksuAknG12αsuAksnK12αsuAksn2D1αsuAnH1nksuAkn1

1.4缆绳方程

深水锚在海床中的动力行为不仅取决于锚和海床土的物理特性，同时受到安装缆绳的影响，尤其是其嵌入在海床中的部分，即嵌入缆。由于海床土的抗力和摩擦作用，嵌入缆在海床中形成反悬链形态[9]，如图2所示。嵌入缆与锚在系缆点处发生相互作用。随着深水锚嵌入深度的增大，系缆点处拖曳力和拖曳力与水平面的夹角θah均增大，从而使得垂直锚板平面的分力增大，促使锚板抬平，对锚的行为造成显著影响。通过引入缆绳方程来考虑缆绳对锚动力行为的影响。

Neubecker等[10]和Zhang等[11]提出了系缆点处拖曳力Ta与θah的关系式：

式中：μ为缆绳-土摩擦系数，在饱和黏土中，Neubecker等[10]和Zhang等[11]分别建议μ取0.4～0.6和0.1～0.6；铁链和钢缆的摩擦系数μ的取值也不同，DNV[12]建议，对钢缆取0.1～0.3，对铁链取0.6～0.8；θe为嵌入点处拖曳力与水平面的夹角；za为系缆点深度；对于拖缆有效承载系数En，Degenkamp等[13]基于模型试验，建议对钢缆取1，对铁链取2.5；d为缆绳直径；Ncl为缆绳端阻力系数。

根据物理实际，系缆点拖曳力与水平面的夹角θah和锚板方位角θo始终存在如下关系：

2 关键技术

关键技术包含两部分内容。首先，介绍最小力准则及其应用：1)用于判断锚的拔出、嵌入方向和旋转中心；2)作为拔出、旋转、嵌入行为是否发生的判定条件。其次，给出深水锚在海床中复杂动力行为的分析流程。

2.1最小力准则

对深水锚复杂动力行为机理的正确认识是研究其综合行为的基础。根据第1节内容，深水锚的综合行为可视为拔出、旋转和嵌入行为的组合，但拔出、嵌入方向和旋转中心的位置，以及拔出、旋转和嵌入行为发生的条件，仍然需要合理确定。对此，本节运用了“最小力准则”，即物体总是趋向于按最容易发生运动的状态进行运动，对于深水锚在海洋土中的复杂动力行为，“最容易”发生运动的状态即为拖曳力最小时的状态。该准则在分析拖曳锚的嵌入运动方向[14]和吸力锚的破坏模式[15]中已有成功应用。

2.1.1 拔出和嵌入时锚的运动方向

拔出、嵌入时的最小力准则是其第一层含义的应用，假设深水锚有一系列可能的运动方向，真正的运动方向是使其最容易发生运动的方向，即当拔出或嵌入拖曳力最小时的运动方向。

由式(2)、(5)可知，拔出、嵌入时的拖曳力Tt为θm的函数。通过研究Tt对θm的一阶导数，可确定使拔出、嵌入拖曳力最小的真实破坏方向角θm：

其中，Tt(θm)=(dFb/dθm+dFs/dθm)cos(θa+θm)+(Fb+Fs)sin(θa+θm)-Wcos(θa-θo),拔出时-π-θ0≤θm<-θ0，嵌入时-θo≤θm≤π-θo。

Tt(拔出、嵌入分别对应Tp和Td)的最小值仅可能在以下特定点取得：

1)边界点，对于拔出即θm=-π-θo和θm=-θo，对于嵌入即θm=-θo和θm=π-θo；

2)满足方程dTt/dθm=0的点，对于拔出即dTp/dθm=0，对于嵌入即dTd/dθm=0；

3)一阶导数不存在的点。

根据“最小力准则”，在这三类特定点中，最小值min(Tp)和min(Td)对应的θm值即为锚真实的拔出和嵌入方向。

2.1.2 旋转时的旋转中心

旋转时的最小力准则也是其第一层含义的应用，假设深水锚有一系列可能的旋转中心，真正的旋转中心是使其最容易发生旋转的旋转中心，即当旋转拖曳力最小时的旋转中心。令Wb=Fb(Lk)·DFb(Lk)，Ws=Fs(Lk)·DFs(Lk)，其中，Fb(Lk)、DFb(Lk)分别代表广义的端阻力、端阻力矩，Fs(Lk)、DFs(Lk)分别代表广义的剪切力、剪切力矩。由式(7)、(8)可知，嵌入拖曳力Tk为Lk的函数，通过研究Tk对Lk的一阶导数，可确定使旋转拖曳力最小的真实的旋转中心位置：

其中，Tk(Lk)=dFb/dLk·DFb+dDFb/dLk·Fb+dFs/dLk·DFs+dDFs/dLk·Fs，0≤Lk≤Lc。

同理，Tk的最小值仅可能在以下特定点取得：

1)边界点，即Lk=0和Lk=Lc；

2)满足方程dTk/dLk=0的点；

3)一阶导数不存在的点。

根据“最小力准则”，在这三类特定点中，Tk取得最小值min(Tk)时的Lk值即为锚真实的旋转中心到锚尾端中心点的距离。

2.1.3 拔出、旋转和嵌入的判定条件

深水锚在任意时刻发生拔出、旋转还是嵌入，仍采用最小力准则判定。若min(Tp)、min(Tk)、min(Td)其中一个力小于另外两个，则发生较小力对应的行为。以图7(a)为例，若min(Tp)min(Td)三种情况。

2.2深水锚复杂动力行为的分析流程

深水锚复杂动力行为的计算流程如下：

1)给定初值，包括初始状态下深水锚的位置z、方位角θo、拖曳力与锚板上表面的夹角θa。

2)最小力第一层含义的应用：在当前条件下，假设发生拔出或嵌入，计算所需的拖曳力min(Tp)、min(Td)及对应的运动方向；假设发生旋转，计算所需的旋转拖曳力min(Tk)、旋转中心位置。

3)最小力第二层含义的应用：比较拔出或嵌入所需拖曳力min(Tp)、min(Td)和旋转所需拖曳力min(Tk)的大小，根据图7所示的各力大小相对关系，判断锚的运动行为。

4)根据步骤3)所判定的行为，给定对应的角度和位移增量；同时根据缆绳方程，即方程(9)，更新系缆点处拖曳力与水平面的夹角θah。

5)重复步骤2)～4)，直至满足结束条件，即锚板抬平或达到极限嵌入深度。

图7 拔出、旋转和嵌入行为的组合Fig. 7 Combination of pulling out, keying and diving

3 模型验证

为检验本文所提出分析模型的合理性，本节将其应用于预测拖曳锚在海床中的嵌入运动轨迹，并与已有分析方法和离心机试验结果进行对比。

3.1与已有分析方法比较

Murff等[16]于2005年公布了一项对于某简化典型拖曳锚的轨迹研究结果，该研究包含5家研究机构或个人的工作成果，随后，Liu等[17]也对此典型锚做了轨迹预测。不同研究者采用的研究方法差别较大，但所预测轨迹的总体趋势相似。其中，预测者1、2、4、5采用极限平衡法，预测者3采用塑性上限分析法，Liu等[17]从运动学入手，采用理论解析方法进行求解。

算例1中所采用的拖曳锚如图8所示，锚的参数见表4，模型计算所需参数见表5。其中，Zued为拖曳锚的极限嵌入深度；b为有效缆绳宽度，b=En·d。拖缆为钢缆，根据DNV[12]的建议，μ的取值在0.1～0.3之间，取平均值0.2。Murff等[16]给出α的取值范围为0.3～0.5。NclNcf的取值没有明确给出，因其直接影响拖曳轨迹的预测，因此有必要对其进行讨论。鉴于对锚和缆绳的端阻力系数认识有限，本文借鉴以往研究者的做法[10,18]，对Ncl和Ncf的取值不作区分，取Nc=Ncl=Ncf。对于深埋条形锚板，Rowe[19]建议Ncf取10.28～11.42。在理论计算拖曳锚所受土抗力时，Neubecker等[3]取Ncf=9。对于表面粗糙的深埋平板，Merifield[20]建议Ncf取11.16～11.86。对于深嵌矩形锚板，O’Neill等[8]建议Ncf取11.87。Elkhatib等[21]认为，深埋锚板的Ncf值与锚板的宽厚比相关，建议取值范围为9.1～11.7。Thorne[4]和Ruinen[22]在研究拖曳锚的嵌入轨迹时，直接采用Skempton[7]的建议值，即Ncf=7.6。综上，Nc的建议取值范围为7.6～11.87。需要说明的是，Liu等[17]所提出的解析解中所需参数θa通过Zhang等[11]的方法求得。计算求得θa=58.7°。

对本文分析模型进行的参数考察结果显示，对拖曳锚而言，极限嵌入深度随Nc的减小而增大，随α的增大而增大，这与之前研究者的结论一致[18]。因此，对于算例1，本文分析模型极限嵌入深度的上限在Nc=7.6，α=0.5时取得；下限在Nc=11.87，α=0.3时取得。对比结果如图9所示。

可以看出，本文的预测结果与6位预测者的预测结果总体趋势一致，即嵌入深度随拖曳距离增加逐渐增大，并最终到达一个极限值。同时，本文预测的轨迹在6位其它预测者曲线范围之间。由此验证了本文所提出分析模型的合理性和有效性。

表4 算例1锚参数表Tab. 4 Anchor parameters for case 1

表5 算例1对比工况表Tab. 5 Parameters for case 1

图8 算例1锚板示意Fig. 8 Schematic of the anchor for case 1

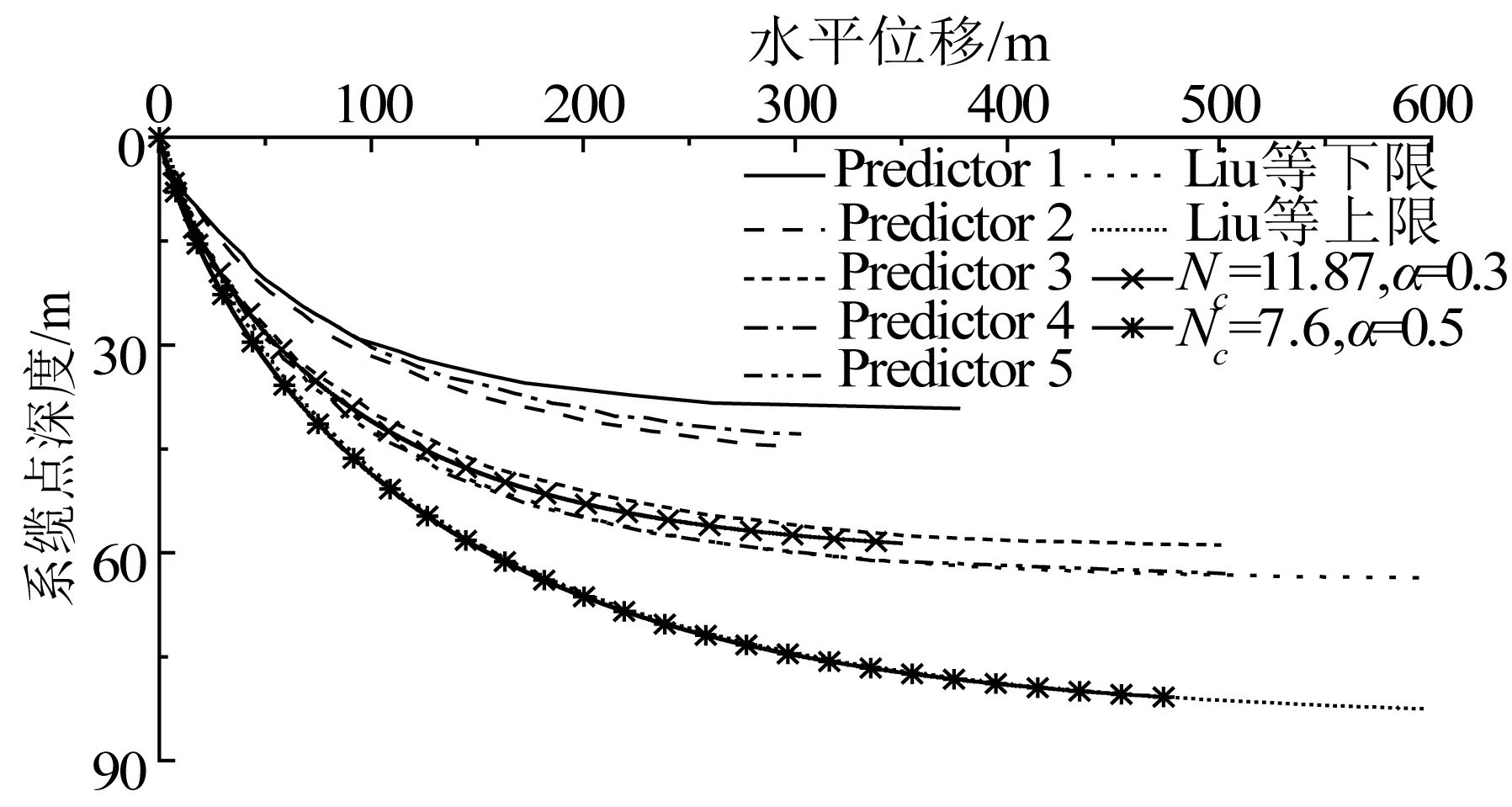
图9 算例1运动轨迹对比Fig. 9 Comparison of the anchor trajectory for case 1

3.2与鼓式离心机试验比较

O’Neill等[23]于2001年采用鼓式离心机试验研究Vryhof Stevpris锚的运动轨迹，本节将分析模型的预测结果与该试验数据进行对比。鼓式离心机试验所用拖曳锚的比尺为1∶160，原型锚自重为32 t，锚胫角分别为32°和50°，锚的楔形角θm为9.7°。模型锚主体尺寸如图10所示。试验所用土体为正常固结黏土，计算所需参数如表6所示。

试验采用特殊设计的加载刚臂控制系缆点坐标，控制方程采用缆绳方程(9)的简化形式：

在算例2中，锚的所有参数和土体参数均已知，但黏滞系数α没有给出。根据Murff等[16]在数值预测拖曳锚在黏土中的运动轨迹时的建议，α取0.3～0.5。为达到预测效果，α分别取0.3和0.5进行对比。

该研究还采用数值增量迭代方法[3]对锚的嵌入行为进行了描述。归一化后的轨迹对比结果如图11所示。

可以看出，运用分析模型预测的拖曳轨迹与试验结果和增量数值模拟结果吻合很好。在对α的考察结果中显示,α=0.3使得分析模型的预测结果与试验结果更为接近。

图10 算例2模型锚主体尺寸图Fig.10 Dimensions of the anchor models for case 2

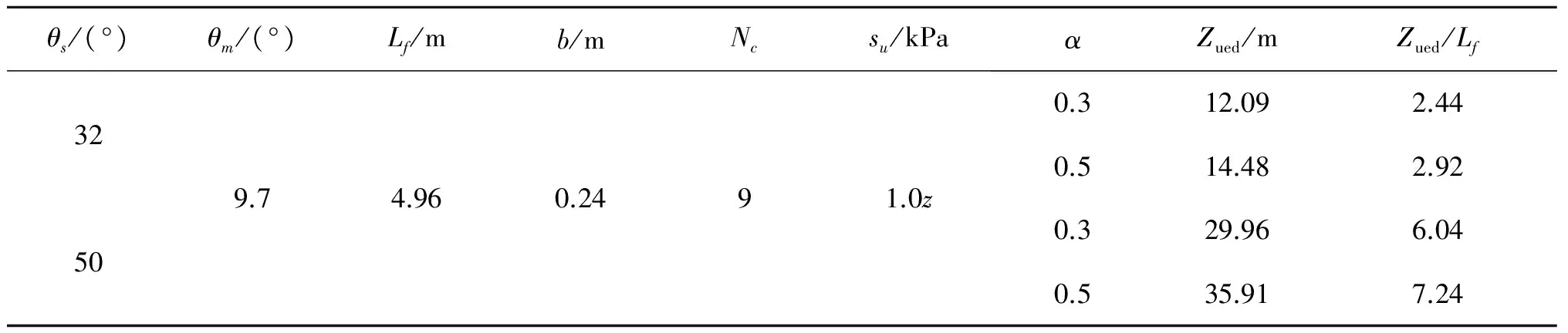
θs/(°)θm/(°)Lf/mb/mNcsu/kPaαZued/mZued/Lf32509．74．960．2491．0z0．312．092．440．514．482．920．329．966．040．535．917．24

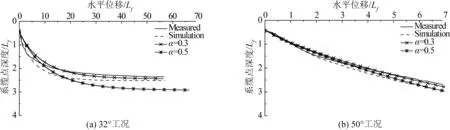
图11 算例2运动轨迹对比图Fig. 11 Comparisons of the anchor trajectories for case 2

4 结 语

1)将深水锚的复杂动力行为分解为拔出、旋转和嵌入，分别给出了明确定义并建立了力学模型。

2)提出最小力准则用于确定锚的拔出、嵌入方向和旋转中心，该准则同时可作为拔出、旋转、嵌入行为是否发生的判定条件。给定分析流程，建立起描述深水锚在海床中复杂动力行为的分析模型。

3)为验证本文提出的分析模型，将其应用于预测拖曳锚的嵌入运动轨迹，预测结果与已有分析方法和离心机试验结果均有较好的吻合，表明了该分析模型的合理性和有效性。

4)该分析模型囊括了已有深水锚在海床中的综合动力行为。将该模型应用于深水锚更为复杂的动力行为，如重力贯入锚在安装过程、系泊状态尤其在极端环境下的行为预测，将是今后工作的重点。

[1] ZIMMERMAN E H, SMITH M W, SHELTON J T. Efficient gravity installed anchor for deepwater mooring[C]//Proceedings of the 41st Annual Offshore Technology Conference. 2009：OTC20117.

[2] STEWART W P. Drag embedment anchor performance prediction in soft soils[C]//Proceedings of the 24th Annual Offshore Technology Conference. 1992：241-248.

[3] NEUBECKER S R, RANDOLPH M F. Performance of drag anchor and chain systems in cohesive soil[J]. Marine Georesources and Geotechnology, 1996, 14：77-96.

[4] THORNE C P. Penetration and load capacity of marine drag anchors in soft clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124：945-953.

[5] AUBENY C P, CHI C. Mechanics of drag embedment anchors in a soft seabed[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136：57-68.

[6] CASSIDY M J, GAUDIN C, RANDOLPH M F, et al. A plasticity model to assess the keying of plate anchors[J]. Geotechnique, 2012, 62：825-836.

[7] SKEMPTON A W. The bearing capacity of clays[C]//Proceedings of the Building Research Congress. 1951：180-189 .

[8] O’NEILL M P, BRANSBY M F, RANDOLPH M F. Drag anchor fluke-soil interaction in clays[J]. Canadian Geotechnical Journal, 2003, 40：78-94.

[9] REESE L C. A design method for an anchor pile in a mooring system[C]//Proceedings of the 5th Annual Offshore Technology Conference. 1973：OTC1745.

[10] NEUBECKER S R, RANDOLPH M F. Profile and frictional capacity of embedded anchor chains[J]. Journal of Geotechnical Engineering, 1995, 121：797-803.

[11] ZHANG W, LIU H X, ZHAO Y B, et al. Interactional properties between drag anchor and installation line[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140：04013018.

[12] DNV, Design and installation of fluke anchors in clay[S]. 2000.

[13] DEGENKAMP G, DUTTA A. Soil resistances to embedded anchor chain in soft clay[J]. Journal of Geotechnical Engineering, 1989, 115：1420-1438.

[14] LIU H X, ZHANG W, LIU C L, et al. Movement direction of drag anchors in seabed soils[J]. Applied Ocean Research, 2012, 34：78-95.

[15] LIU H X, WANG C, ZHAO Y B. Analytical study of the failure mode and pullout capacity of suction anchors in clay[J]. Ocean Systems Engineering, 2013, 3：79-95.

[16] MURFF J D, RANDOLPH M F, ELKHATIB S, et al. Vertically loaded plate anchors for deepwater applications[C]//Proceedings of International Symposium on Frontiers in Offshore Geotechnics. 2005：31-48.

[17] LIU H X, LIU C L, ZHAO Y B, et al. Reverse catenary equation of the embedded installation line and application to the kinematic model for drag anchors[J]. Applied Ocean Research, 2013, 43：80-87.

[18] LIU H X, LI Y, YANG H T, et al. Analytical study on the ultimate embedment depth of drag anchors[J]. Ocean Engineering, 2010, 37：1292-1306.

[19] ROWE R K. Soil structure interaction analysis and its application to the prediction of anchor behavior[D]. Australia：University of Sydney, 1978.

[20] MERIFIELD R S, SLOAN S W, YU H S. Stability of plate anchors in undrained clay[J]. Geotechnique, 2001, 51：141-154.

[21] ELKHATIB S, RANDOLPH M F. The effect of interface friction on the performance of drag-in plate anchors[C]//Proceedings of International Symposiumon Frontiers in Offshore Geotechnics. 2005：171-177.

[22] RUINEN R M. Penetration analysis of drag embedment anchors in soft clays[C]//Proceedings of International Offshore and Polar Engineering Conference. 2004：531-537.

[23] O’NEILL M P, RANDOLPH M F. Modelling drag anchors in a drum centrifuge[J]. International Journal of Physical Modeling in Geotechnics, 2001, 2：29-41.

An analytical model of comprehensive kinematic behaviors of deepwater anchors in the seabed

SONG Haijuan, LIU Haixiao, ZHAO Yanbing

(School of Civil Engineering, Tianjin University, Tianjin 300072, China)

Deepwater anchor is the core component of deepwater mooring system. With the development of new concepts and technologies in the field of deepwater mooring, the kinematic behavior of deepwater anchors in the seabed becomes more complicated, which brings great challenges to the published analytical methods. The comprehensive kinematic behavior of deepwater anchors is herein regarded as the combination of well-defined Pulling out, Keying and Diving, whose mechanical models are developed respectively. The “Minimum force principle” is proposed not only to determine the directions of pulling out and diving and the center of rotation, but also to serve as the criteria for whether Pulling out, Keying and Diving will occur. Thus an analytical model is established to describe the comprehensive kinematic behavior of deepwater anchors in the seabed. By applying the analytical model to predict the kinematic trajectory of drag anchors in the seabed and comparing the results with the published analytical methods and centrifuge test data, the validity of the analytical model is verified.

deepwater anchor; kinematic behavior; analytical model; kinematic trajectory; seabed

P751

A

10.16483/j.issn.1005-9865.2015.06.005

刘海笑，男，博士生导师，主要从事深水系泊技术和海洋岩土工程方面的研究。E-mail: liuhx@tju.edu.cn

1005-9865(2015)06-035-10

2014-10-21

天津市应用基础与前沿技术研究计划重点项目(14JCZDJC39900)；国家自然科学基金资助项目(51179124)

宋海娟(1990-)，女，山东潍坊人，硕士生，从事海洋工程系泊基础方面的理论研究。E-mail: song_hai_juan@163.com