老龄半潜式钻井平台节点疲劳裂纹扩展寿命预报

梁园华，杨清峡，闫小顺，杨 蕖，李洛东

(1. 中国船级社海工技术中心，北京 100007； 2. 上海交通大学 海洋工程国家重点实验室，上海 200240)

老龄半潜式钻井平台节点疲劳裂纹扩展寿命预报

梁园华1，杨清峡1，闫小顺2，杨 蕖1，李洛东1

(1. 中国船级社海工技术中心，北京 100007； 2. 上海交通大学 海洋工程国家重点实验室，上海 200240)

通过结合常规谱疲劳分析方法和裂纹扩展分析方法，给出了一种工程实用的评价老龄平台节点裂纹扩展寿命的方法，并以某一平台为例进行了验证计算。首先，基于谱疲劳分析得到各个节点在过去30年的节点疲劳损伤，然后，对损伤接近或大于1.0的节点进行基于单一曲线模型的裂纹扩展分析，以求得该节点在目前状态下裂纹扩展寿命。结果表明，目标平台计算疲劳热点满足继续使用的要求。此外，针对不同初始裂纹尺寸时的裂纹扩展寿命计算结果表明初始裂纹尺寸对疲劳裂纹扩展寿命影响很大。

疲劳裂纹扩展；单一曲线模型；谱分析；半潜式平台；疲劳损伤；平台节点；寿命预测

随着海洋资源的开发，海洋平台等海洋结构物逐渐增多。为了尽可能地发挥现有平台作用以满足我国海洋开发需要，在保证安全的前提下设法延长海洋平台的使用寿命成为我国业界的一个主要挑战。对于老龄平台，疲劳破坏是主要的破坏模式之一，疲劳强度校核也成为各大船级社的重要内容，如何准确合理预报海洋结构物疲劳寿命也成为海洋工程领域研究的热点之一。刘刚等[1]对BINGO9000半潜式钻井平台进行了基于S-N曲线和线性累计损伤理论的疲劳分析。马网扣等[2]归纳了基于全概率谱分析法直接计算疲劳寿命的基本步骤，并对某深水半潜平台进行了疲劳强度校核。谢文会等[3]对比了简化疲劳分析和常规疲劳谱分析方法，得到简化分析偏于保守的结论。Liu等[4]则针对liuhua11-1半潜式生产平台延寿中的节点疲劳强度进行了4个作业阶段的谱疲劳损伤计算。Ahmadi等[5]基于S-N曲线和线性累计损伤理论，研究应力集中系数对海洋导管架结构疲劳可靠性预报的影响。Muhammed等[6]则研究了海洋结构物概率疲劳评估方法，认为可靠性评估的不确定性主要取决于热点应力评估的不确定性。Gholizad等[7]基于累计损伤理论研究疲劳失效形式，并研究平台系统失效概率的计算方法。

然而基于S-N曲线和线性累计损伤理论的疲劳分析方法不能考虑初始缺陷的影响，也无法合理解释老龄平台疲劳评估中普遍遇到的一个问题：对于累积疲劳损伤接近甚至超过1.0的节点，该节点在还未发现裂纹或者在裂纹修复后还能使用多久？因此基于裂纹扩展原理的疲劳评估方法越来越受到业界的重视。黄小平等[8]提出海洋钢结构裂纹扩展率单一曲线模型。崔磊等[9]则运用单一曲线模型对某半潜平台典型节点进行裂纹扩展寿命预报，并得到裂纹扩展理论可用于深水半潜平台疲劳评估的结论。李良碧等[10]基于Paris公式对海洋平台典型节点进行疲劳寿命预报。Aminfar[11]基于断裂力学和可靠性理论，研究了应力集中系数对海洋管节点结构裂纹扩展寿命可靠性预报的影响。针对老龄平台疲劳评估中碰到的上述问题，本文提出了一种结合传统S-N曲线谱疲劳分析和断裂力学分析的方法，即先对目标平台在以往营运历史中的节点疲劳寿命进行基于S-N曲线的谱疲劳分析，对于那些累积疲劳寿命接近或超过1.0的节点，则采取基于节点目前状态的裂纹扩展分析，以获得该节点的裂纹扩展寿命，从而为平台延寿使用的科学决策提供依据，并以某半潜平台实际延寿评估为例，先对平台进行谱分析，得到波浪诱导应力范围的长期分布，然后结合单一曲线模型，考虑载荷比、应力强度因子门槛值、焊接残余应力的影响，对某半潜平台立柱与撑管连接的位置进行基于裂纹扩展的寿命预报，并在此基础上讨论了初始裂纹尺寸对疲劳寿命的影响。

1 基于裂纹扩展的寿命预报

1.1单一曲线模型

BS7910[12]为了准确描述门槛值附近的扩展速率而采用双线性模型，这种方法将扩展速率分成好几段，不便于船舶在随机载荷幅值下的裂纹扩展寿命预报。黄小平等[8]提出的单一扩展率模型不仅将BS7910中的三段用一个公式描述，而且能考虑应力比、门槛值、载荷次序等的影响，兼具简洁性和工程实用性。单一曲线模型的表达式：

式中：ΔKeq0，ΔKth0为等效于应力比R=0时的等效应力强度因子幅和应力强度因子幅门槛值；C为Paris系数，m为裂纹扩展指数；MR为载荷比的修正因子；β，β1为环境参数，根据材料裂纹扩展率数据得到；MP为载荷次序的修正因子，不考虑超载的影响时可取MP=1。

1.2应力强度因子求解

应力强度因子是裂纹扩展率中的重要参数，焊趾处应力强度因子幅一般可用下式表示：

式中：s表示结构受到的循环名义应力范围，a表示裂纹特征尺寸，Y表示应力强度因子修正系数，Mk表示应力强度因子焊趾放大系数。对于受均匀拉伸应力作用的T型焊接接头(一半模型示意图如图1所示)而言，Y通常采用Newman-Raju公式[13]，而应力强度因子焊趾放大系数则通常采用BS7910[12]推荐的公式，即：

式中各参数意义如图1中所示，求解方法参考BS7910[12]。

对于海洋工程结构而言，管节点常常是疲劳的热点区域。如图2所示的T型管焊接接头，求解其冠点焊趾处三维表面裂纹应力强度因子暂时没有权威的经验公式可供利用。本文运用子模型法对冠点焊趾处的表面裂纹进行求解，带表面裂纹的三维子模型如图3所示。其中，粗模型用壳单元建立，带表面裂纹的子模型用体单元建立，边界条件则根据粗模型计算结果插值得到。

计算出的应力强度因子与T型焊接接头经验公式进行对比，结果如图4所示。可以看出，由于相贯的两个管直径都比较大，计算该T型管节点焊趾处表面裂纹的应力强度因子与T型平板焊接接头经验公式计算的结果相近(误差不超过15%)，而且相对T型平板焊接接头较小。因此，在海洋工程结构基于断裂力学的疲劳评估方法中，直接用T型平板焊接接头经验公式求解图2所示冠点焊趾处的表面裂纹应力强度因子是可行的。

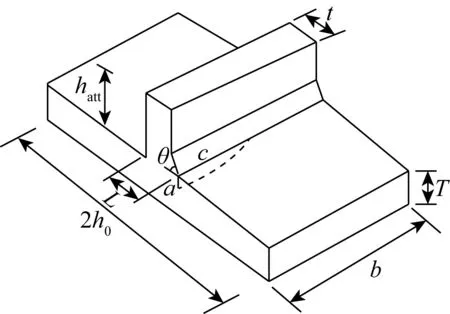
图1 T型平板焊接接头一半模型示意Fig. 1 Schematic diagram of the half model of T-plate joint

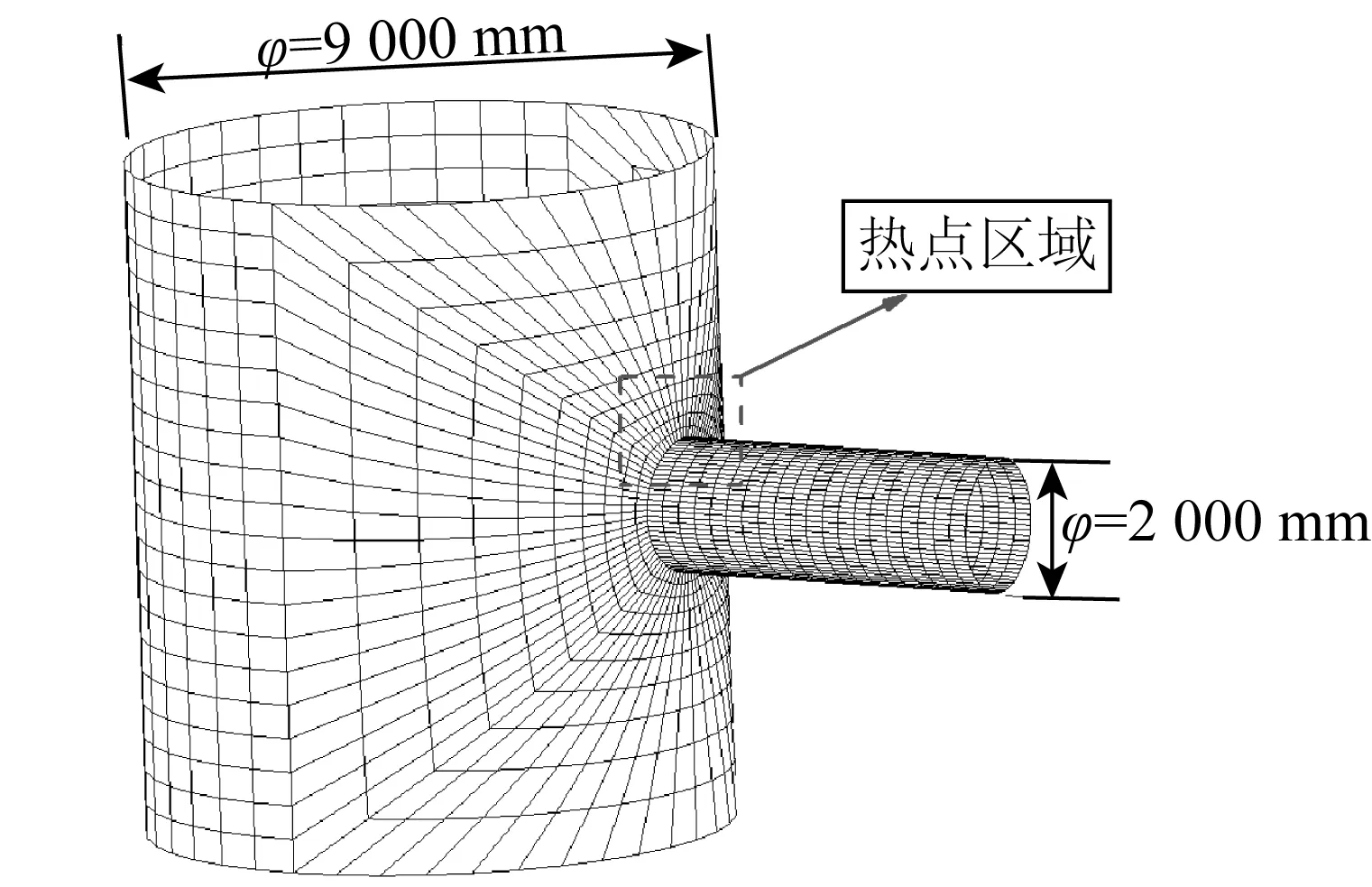
图2 T型管节点示意Fig. 2 Schematic diagram of T-tube joint

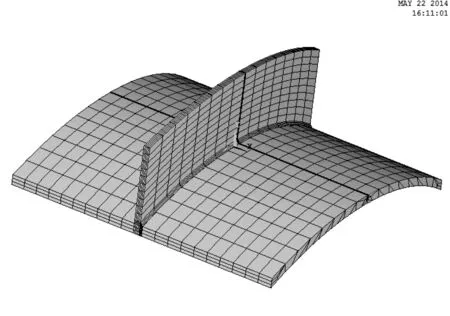
图3 T型管冠点带裂纹子模型Fig. 3 Sub-model of T-tube joint

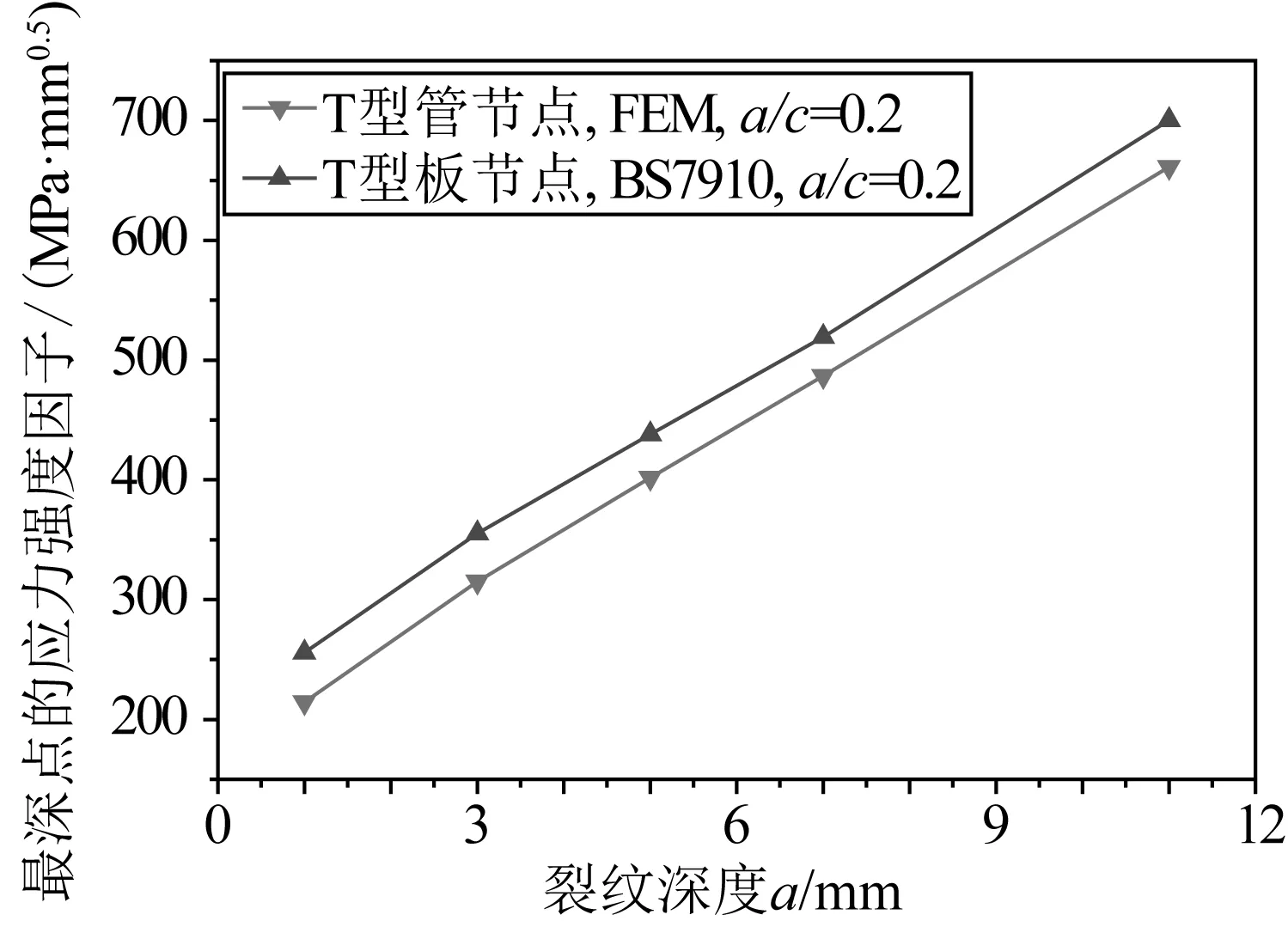
图4 表面裂纹应力强度因子对比曲线Fig. 4 Comparison of stress intensity factor

2 应力范围的长期分布

一般认为波浪诱导应力范围的长期分布服从双参数的Weibull分布，分布函数为：

式中形状参数h一般是根据平台所处的海洋环境、结构类型，响应特性以及构件在整个结构中的位置等因素来确定的。到目前的研究结果表明，形状参数的取值一般是在0.7～1.4之间，通常可通过详细的应力谱分析或者通过经验取得[14]。而尺度参数q可用回复期(n0)内疲劳载荷长期分析得到的对应某一超越概率的应力范围Δσn0表示，可用以下方法计算：

因此，只需要确定Weibull分布的形状参数和回复期内的最大应力范围即可。

常规经验公式法是，用经验公式来计算目标疲劳热点的形状参数h，然后结合回复期(n0)对应某一超越概率的应力范围Δσn0(可由经验值或设计波法计算得到)，运用式(7)计算得到尺度参数q。

另一种是由谱分析法拟合得到。谱分析法建立在真实的海况、真实的装载基础上的直接计算方法, 涉及水动力和有限元分析, 而且考虑不同的波频和浪向组合后的工况, 理论上更加完善，精度相对较高，本文运用此方法。其基本步骤如下[14]：

1) 计算疲劳热点应力传递函数H(ω|θ)，即直接计算疲劳节点的热点应力在各个波频ω、各个浪向角θ时单位波幅下的传递函数。

2) 确定疲劳应力能量谱S(ω|Hs,Tz,θ)

式中：Sη(ω|Hs,Tz)表示波浪谱；Hs表示有义波高；Tz表示平均跨零周期。

3) 计算谱矩。第n阶谱矩mn：

4) 假定各个短期海况的应力响应符合Rayleigh分布，其概率密度函数形式如下：

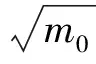
5) 结合海洋平台工作海域的波浪散布图和各浪向出现的概率，累加即可得到应力范围的长期分布。然后拟合得到式(6)中的形状参数h和尺度参数q。

3 半潜平台典型节点预报

某半潜式钻井平台建造于1984年，到2014年已经实际服役30 a。疲劳评估先对目标平台筛选出的54个热点进行基于以往营运历史的S-N曲线谱疲劳分析。结果显示，撑管与立柱的连接处(如图5所示)的两个热点疲劳寿命仅为30 a(见表1)，不满足平台继续营运要求，其它热点最小寿命为54 a，满足平台继续营运要求。因此选取如图5所示的焊接接头为阐述对象。

表1 平台中立柱上热点处疲劳寿命Tab. 1 Fatigue life of hot spots located on the middle column

3.1疲劳载荷谱

建立半潜平台湿表面模型，在ANSYS AQWA/WAVE中进行水动力分析。水动力分析参数如下：

波率：0.2 ～1.8 rad/s，步长为0.1 rad/s (共17个频率)；

浪向：-180°～150°, 步长为30° (共12个浪向)；

波高：单位波高。

采取实部和虚部加载所得到的响应合成的方法，一共进行408次(17×12×2)水动力分析。然后将湿表面上的压力映射到PATRAN有限元整体粗糙模型上，经加载、计算，得到不同浪向、不同频率的单位波高的波浪载荷下的应力响应。然后建立疲劳热点附近结构的详细模型(如图5所示)，应用PATRAN场加载方法，将不同浪向、不同频率单位波高的波浪载荷响应映射到细模型边界上，作为细模型计算的边界条件。其中PATRAN粗糙模型用壳单元和梁单元建立，而详细模型均采用壳单元建立，平台所用钢材的屈服强度均为245 MPa、材料弹性模量E=206 GPa、泊松比μ=0.3。图6为浪向-120°、频率0.8 rad/s、实部的波浪载荷下，目标热点附近细模型的等效应力云图。

目标热点的最大主应力传递函数曲线如图7所示。本文谱分析时，波浪谱根据要求选用ITTC推荐的两参数P-M谱，波浪散布图选用海洋平台工作区域的散布图。根据第二部分所述步骤，得到应力范围的长期分布，然后拟合成两参数的Weibull分布，结果如图8所示。

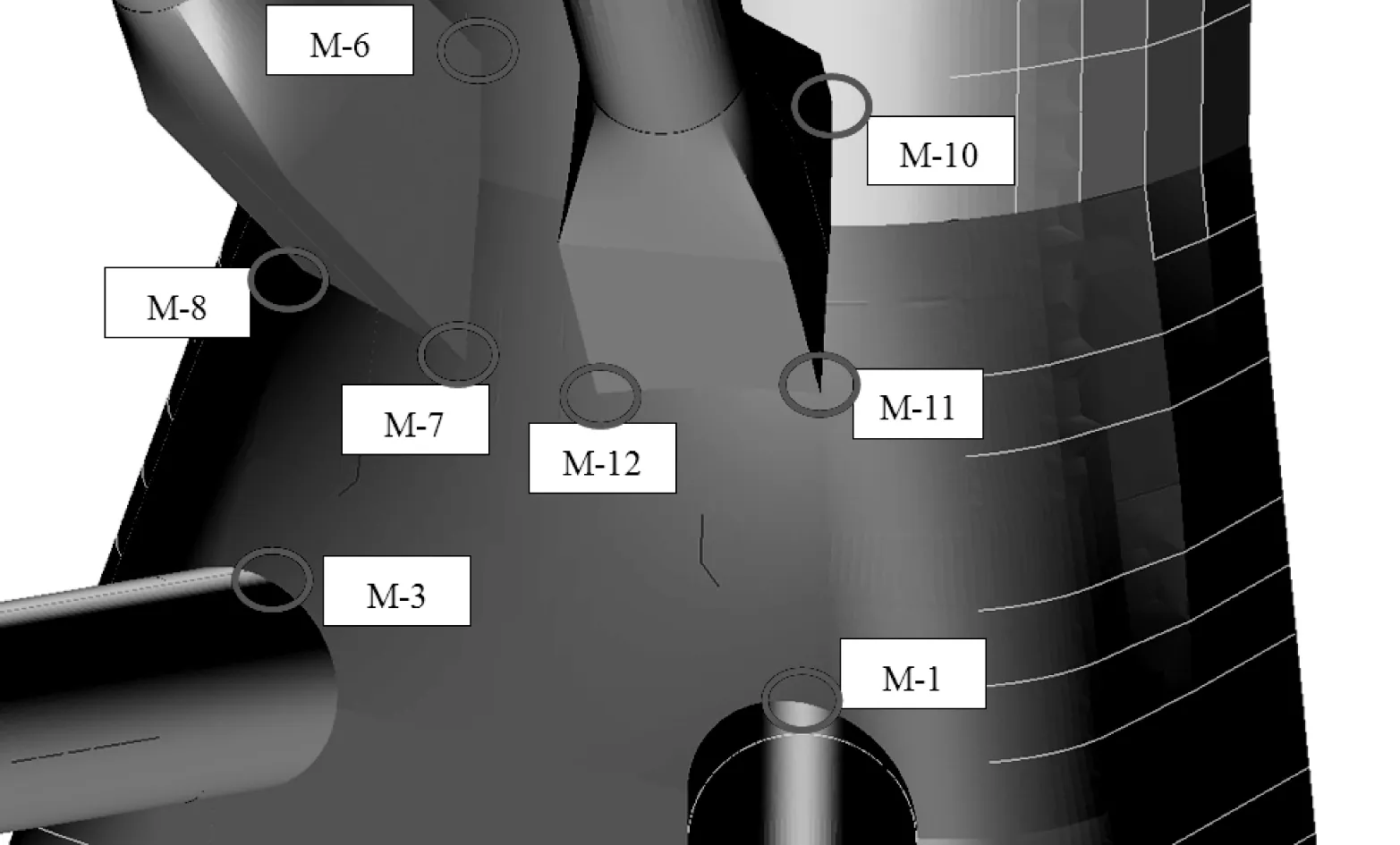
图5 目标热点位置Fig. 5 Location of the target hot spot

图6 某工况下的等效应力云图Fig. 6 Von Mises contours of a load condition

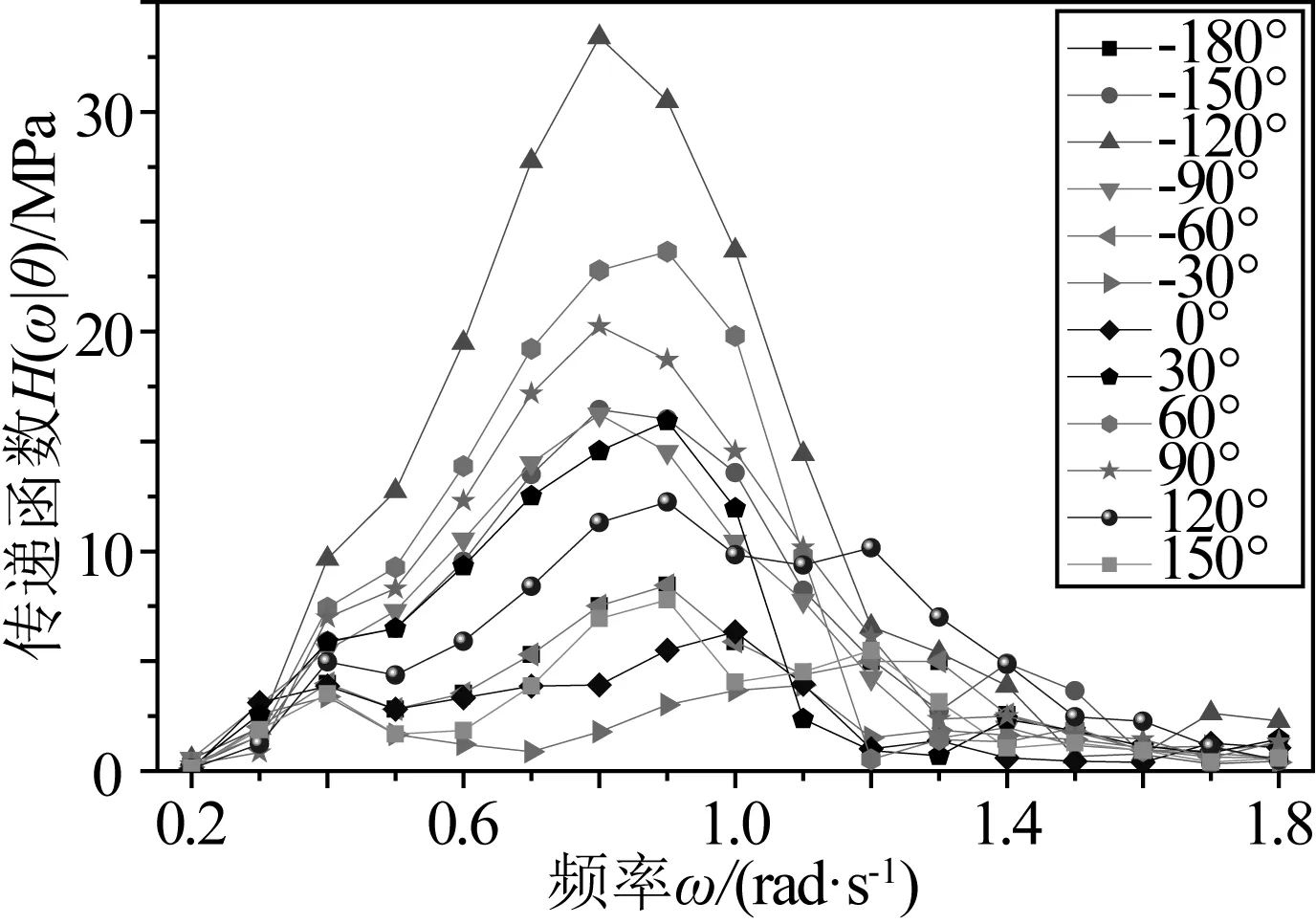
图7 传递函数曲线Fig. 7 Curves of transfer function

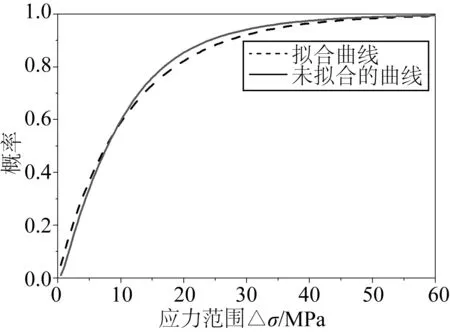
图8 应力范围长期分布图Fig. 8 Long-term distribution of wave-induced stress ranges

3.2疲劳裂纹扩展预报

裂纹扩展计算采用单一曲线模型。其中Paris系数C、裂纹扩展指数m、等效应力比为0的应力强度因子幅门槛值ΔKth0均参考国际焊接协会(IIW[14])推荐的值，即C=5×10-13，m=3，ΔKth0=190 MPa·mm0.5。载荷比修正因子计算中的参数β=0.3，β1=0.5，本文计算暂不考虑载荷次序的影响。

根据中国船级社规范[13]的建议，当没有测量数据时，表面裂纹深度a0取0.5 mm，裂纹深度和长度的比例a0/2c0为0.2。出于安全考虑，假定应力垂直于裂纹面，仅考虑拉伸应力的影响。当裂纹穿透板厚时，构件发生疲劳破坏。通过自编程序进行扩展计算，裂纹扩展曲线如图9所示。

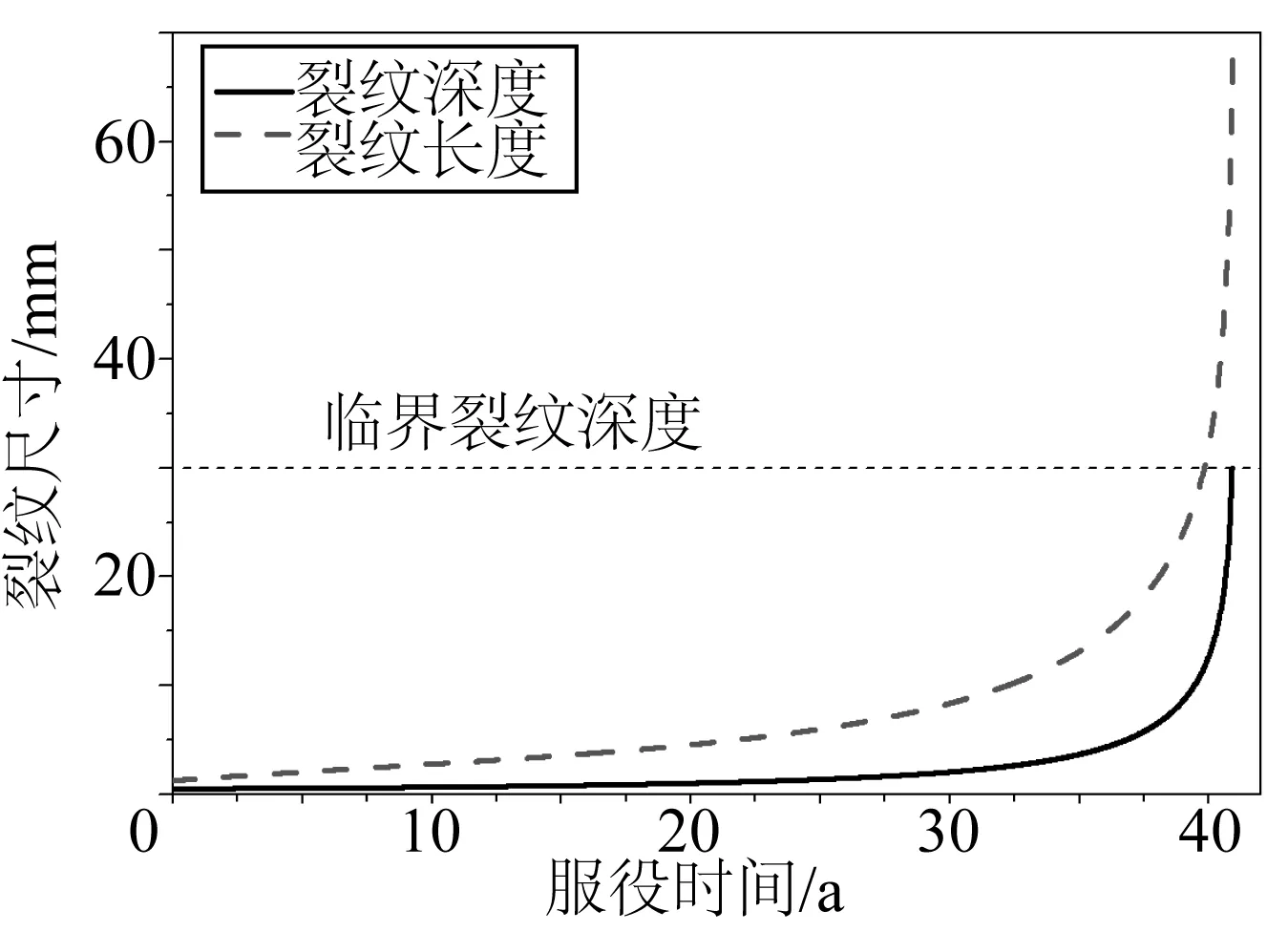
图9 目标热点裂纹扩展曲线Fig. 9 Crack growth curve of the target hot spot

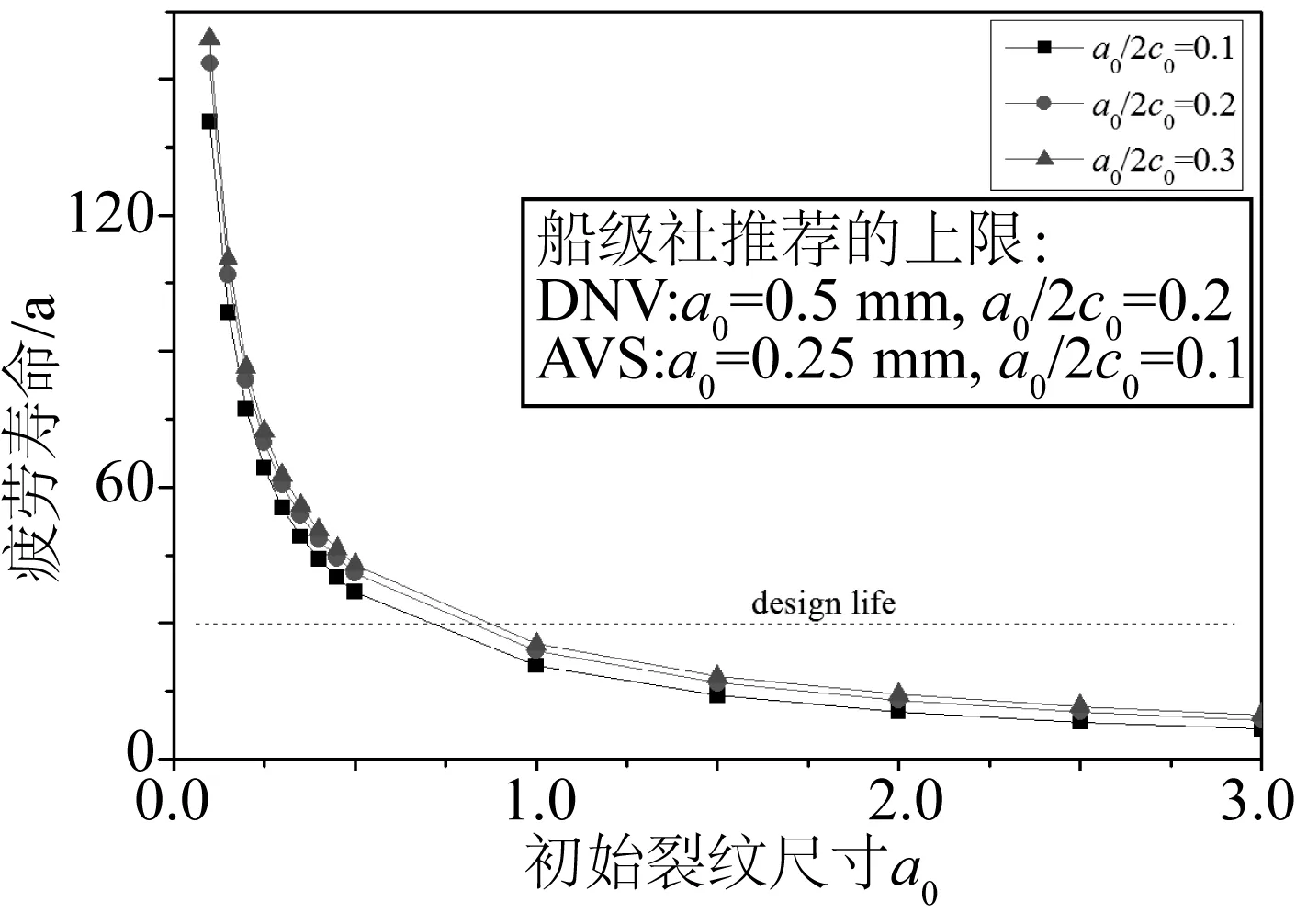
图10 不同尺寸的初始裂纹疲劳寿命Fig. 10 Fatigue lives of different initial crack sizes

可以看到，裂纹开始扩展缓慢，而在服役后期迅速扩展，构件的疲劳寿命大约需要40 a，满足设计寿命的要求。另外，由于在裂纹扩展计算中许多参数本身存在很大的不确定性，这也必然导致计算的结果存在较大不确定性。但是，文中计算参数大都取参数的保守值，计算结果应该也趋于保守。

3.3初始裂纹尺寸的影响

当没有已测的数据时，规范通常推荐对焊缝区的裂纹初始深度a0取0.1～0.25 mm之间，初始深度和长度的比例a0/2c0取0.1。当初始裂纹深度以及初始裂纹深度与长度的比例取不同值时，疲劳裂纹扩展寿命如图10所示。可以看出，随着初始裂纹深度的增加，疲劳寿命逐渐减小，而且当裂纹较小时，疲劳寿命随着初始裂纹尺寸的增加减小的速度很快，因此，控制小裂纹的深度对降低结构疲劳破坏的风险是非常重要的。同时可以看到，疲劳寿命随着初始裂纹深度与长度的比例的增大而增大，但增幅不大。

4 结 语

通过结合传统谱疲劳分析方法和裂纹扩展分析方法，解决了在老龄半潜式平台延寿中节点疲劳寿命按照谱疲劳分析方法计算的损伤度超过或接近1.0时如何决策的问题。针对某一实际半潜式平台，对平台典型节点进行了基于裂纹扩展的疲劳评估，主要研究内容和结论如下：

1)采用子模型法，计算大直径管-管相贯冠点焊趾处表面裂纹应力强度因子，并与T型板焊接接头经验公式对比。结果表明，T型板焊接接头的经验公式，可以运用于本文所讨论的大直径管-管相贯冠点焊趾处表面裂纹应力强度因子的计算。

2)将常规疲劳谱分析法与疲劳裂纹扩展理论相结合，采用谱分析得到的应力范围长期分布构造疲劳载荷谱，运用单一曲线模型预报裂纹扩展曲线，对某平台典型焊接节点进行基于裂纹扩展的寿命预报。结果表明，所讨论的疲劳热点的裂纹扩展寿命满足平台继续使用的要求。

3)通过计算不同初始裂纹尺寸的疲劳裂纹扩展寿命，讨论初始裂纹尺寸对裂纹扩展寿命的影响。结果表明，初始裂纹尺寸对疲劳寿命影响很大，尤其是初始裂纹深度较小时，这一影响更为明显，因此若能结合实测裂纹数据进行预报，将更有意义。本文所取裂纹尺寸为船级社推荐的保守数据，因此预报结果也偏保守。

[1] 刘刚，郑云龙，赵德有，等. BINGO9000 半潜式钻井平台疲劳强度分析[J]. 船舶力学, 2002, 6(2): 54-63. (LIU Gang, ZHENG Yunlong, ZHAO Deyou, et al. Fatigue strength analysis of BINGO9000 semisubmersible drilling rig[J]. Journal of Ship Mechanics, 2002, 6(2): 54-63.(in Chinese))

[2] 马网扣, 王志青, 张海彬. 深水半潜式钻井平台节点疲劳寿命谱分析研究[J]. 海洋工程, 2008, 26(3): 1-8. (MA Wangkou, WANG Zhiqing, ZHANG Haibin. Study on spectrum-based fatigue life direct calculation for spots of deep-water semi-submerged drilling unit[J]. The Ocean Engineering, 2008, 26(3): 1-8.(in Chinese))

[3] 谢文会, 谢彬. 深水半潜式钻井平台简化疲劳分析[J]. 海洋工程, 2010, 28(2): 37-43. (XIE Wenhui, XIE Bin. Simplified fatigue assessment for deepwater semi-submersible rig[J]. The Ocean Engineering, 2010, 28(2): 37-43. (in Chinese))

[4] LIU B, WANG J, YIN H J, et al. Liuhua 11-1 FPS dry-dock upgrade and life extension- fatigue assessment challenges and solutions[C]//OTC24094. 2013:1-10

[5] AHMADI H, LOTFOLLAHI-YAGHIN M A. Effect of SCFs on S-N based fatigue reliability of multi-planar tubular DKT-joints of offshore jacket-type structures[J]. Ships and Offshore Structures, 2013, 8(1): 55-72.

[6] MUHAMMED A, STACEY A. Probabilistic S-N fatigue assessment methods for welded joints in offshore structures[C]//Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers. 2008: 335-354.

[7] GHOLIZAD A, GOLAFSHANI A A, AKRAMI V. Structural reliability of offshore platforms considering fatigue damage and different failure scenarios[J]. Ocean Engineering, 2012, 46: 1-8.

[8] 黄小平, 贾贵磊, 崔维成, 等. 海洋钢结构疲劳裂纹扩展预报单一扩展率曲线模型[J]. 船舶力学, 2011, 15(1): 118-125. (HUANG Xiaoping, JIA Guilei, CUI Weicheng, et al. Unique crack growth rate curve model for fatigue life prediction of marine steel structures[J]. Journal of Ship Mechanics, 2011, 15(1): 118-125. (in Chinese))

[9] 崔磊, 何勇, 毛江鸿, 等. 基于裂纹扩展的深水半潜式平台疲劳寿命分析[J]. 船舶力学, 2013, 17(11): 1318-1327. (CUI Lei, HE Yong, MAO Jianghong, et al. Crack propagation-based fatigue life analysis for deep water semi-submersible platform[J]. Journal of Ship Mechanics, 2013, 17(11): 1318-1327. (in Chinese))[10] 李良碧, 朱红娟, 李增华, 等. 基于裂纹扩展原理的深水半潜平台疲劳寿命分析[J]. 江苏科技大学学报：自然科学版, 2013, 27(1): 1-4. (LI Liangbi, ZHU Hongjuan, LI Zenghua, et al. Fatigue analysis of deepwater semi-submersible platform based on crack propagation[J]. Journal of Jiangsu University of Science and Technology, Natural Science Edition, 2013, 27(1): 1-4. (in Chinese))

[11] AMINFAR M H. Effect of stress concentration factors on the structural integrity assessment of multi-planar offshore tubular DKT-joints based on the fracture mechanics fatigue reliability approach[J]. Ocean Engineering, 2011, 38(17): 1883-1893.

[12] BS7910. Guide to methods for assessing the acceptability of flaws in metallic structures[S]. British Standards Institution, 2005.

[13] NEWMAN Jr J C, RAJU I S. An empirical stress-intensity factor equation for the surface crack[J]. Engineering Fracture Mechanics, 1981, 15(1): 185-192.

[14] 中国船级社. 海洋工程结构物疲劳强度评估指南[S]. 2013. (China Classification Society. Guidelines for fatigue strength assessment of offshore engineering structures[S]. 2013.(in Chinese))

[15] IIW. Recommendations for fatigue design of welded joints and components [S]. International Institute of Welding, 2004.

Fatigue crack growth life prediction for a welded detail on an ageing semi-submersible platform

LIANG Yuanhua1, YANG Qingxia1, YAN Xiaoshun2, YANG Qu1, LI Luodong1

(1. Marine Technology Center of China Classification Society, Beijing 100007, China；2. State Key Lab of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

Based on the traditional fatigue spectral analysis and fracture mechanics analysis, a method to predict the fatigue life of an old drilling platform was provided and applied to a semi-submersible platform. First, the fatigue damage of hot spots during the past 30 years was obtained by using traditional spectral fatigue method, then the fatigue crack growth life was predicted for those hot spots with damage close to or larger than 1.0 by using the unique curve model. The results showed that the fatigue strength of the discussed spots met the requirements. By comparing the fatigue life of welded detail with surface cracks of different initial sizes, the conclusion that the initial size of the crack had a significant impact on the fatigue crack growth life was obtained. The conclusions and method of fatigue life prediction will be helpful for the life-extension of old mobile drilling units.

fatigue crack growth; unique curve model; spectral analysis; semi-submersible platform; fatigue damage; platform joint; fatigue life prediction

P751

A

10.16483/j.issn.1005-9865.2015.06.003

1005-9865(2015)06-020-06

2014-08-26

梁园华(1976-)，男，博士，高级工程师，主要研究方向为海洋工程结构强度。E-mail：yhliang@ccs.org.cn