海底管线水平向整体屈曲及失效判断方法研究

刘 润，洪兆徽，刘文彬

(天津大学 水利工程仿真与安全国家重点试验室，天津 300072)

海底管线水平向整体屈曲及失效判断方法研究

刘 润，洪兆徽，刘文彬

(天津大学 水利工程仿真与安全国家重点试验室，天津 300072)

海底管线是海洋石油的重要输运手段。为满足输送工艺的需要，正常工作条件下管线往往被施加较高的温度和压强，高温高压使管线内产生附加应力，当附加应力大于土体对管线的约束力时，管线就会发生整体屈曲。过度的水平向整体屈曲会导致截面产生较大的弯曲应力和压缩应变，对管线系统的安全运行造成威胁，因此需要对发生水平向整体屈曲后的管线进行验算。采用解析解法、规范法和有限元法对管线的整体屈曲进行分析，提出了应用临界屈曲荷载值域空间和值域下限来判断不同缺陷大小下管线是否发生水平向整体屈曲的方法。结合工程实例，分别采用内力控制标准和位移控制标准对管线水平向整体屈曲后是否失效进行了验算。研究指出，相较于位移标准，内力控制标准更为严格。

海底管线；水平向整体屈曲；临界屈曲判断；屈曲失效判断

随着经济的发展，对油气资源的需求量日益增加，海上油气资源的开发也日益受到重视。海底管线作为一种安全、高效、经济的油气运输手段，在海上油气工程中有着广泛的应用。油气在管线运输过程中常常被施加高温、高压以便于运输，使得管线内产生较大的附加应力，当应力达到一定值后，管线就会发生整体屈曲，过度的整体屈曲会影响管线的功能甚至造成管线的失效，因此需要加以控制。早在20世纪80年代国外学者就开始了关于管线整体屈曲的研究，提出了管线整体屈曲的各阶模态，并通过理论分析，求解了理想管线[1]和具有一定初始缺陷管线[2]发生整体屈曲变形后管线轴力、弯矩和变形幅值与整体屈曲长度的对应关系，推导出管线整体屈曲的临界荷载。随着海洋石油开采由近海向深海发展，管线受水深条件的影响，多为直接裸铺于海床表面不掩埋，因此深海管线多发生水平向整体屈曲，对水平向整体屈曲的分析逐渐成为该领域的热点问题。借助于日渐成熟的计算机技术和大量有限元软件的应用和开发，许多学者通过数值模拟的方法分析了非线性土体约束下管线水平向整体屈曲的成因、形态和影响因素[3-4]。

管土间相互作用力直接影响着管线的整体屈曲，在研究管土约束力时，模型试验和有限元分析应用较为广泛。1986年，Brennodden等[5]在硬黏土、粉质松散细砂、软黏土和中粗砂四种土体中对不埋管线水平向运动时所受约束力进行了试验，得出了土体约束力系数；2005年Bruton等[6]对软黏土中管线在水 平向循环荷载作用下运动的试验表明，软黏土中管线前部会出现较高的土坝，导致土体对管线约束力的显著提高；2011和2013年，刘润等[7-8]对渤海湾土体，采用不同管径、埋深的管线进行了轴向和水平向运动时土体约束力的测定，建立了基于渤海土体的约束力模型；Bransby等[9]于2002年，Cheuka等[10]于2007年利用离心机试验方法，通过小尺寸模型反应真实大小管线的物理行为，对管土相互作用问题进行了深入研究；2007年任艳荣等[11]利用ABAQUS分析了管线水平向运动的管土相互作用，并比对有关实验数据，说明了分析的可靠性；Paul等[12]于2009年，Pike等[13]于2010年运用ABAQUS中的CEL技术，解决了土体大变形问题，为管线稳定设计提供了新的设计思路与设计方法。这些试验和研究，为更好地理解管土相互作用机理，建立正确的土体约束力模型提供了条件，使得整体屈曲的模拟和计算更为精确，结果更为可信。

对于管线的整体屈曲，众多学者对管线在不同管土相互作用模型下发生整体屈曲后的应力状态和屈曲形态进行了大量的研究[14-17]。管线水平向整体屈曲后会产生较大的水平向位移，引起截面的应力集中，危害管线安全。对管线整体屈曲后的校核，仅在部分规范中有所涉及。这里基于对管线初始缺陷与土体约束力模型的研究，结合现有的国际相关规范，针对渤海某实际工程，对现有的两种海底管线水平向整体屈曲临界荷载及屈曲失效判断方法进行了对比，并给出了标准选用时的建议。

1 水平向整体屈曲分析中初始缺陷的引入依据

Taylor和Gan[2]在1986年对具有初始缺陷管线进行了整体屈曲分析，并对缺陷管线和理想管线进行了对比，得出缺陷对于管线强度的影响规律。经分析得出同一根管线在不同大小初始缺陷下，发生整体屈曲后随着整体屈曲幅值的发展会产生不同的轴力—屈曲幅值关系曲线。通常用缺陷的幅值与长度之比(v0/L0)来描述缺陷的大小，对于缺陷v0/L0较小管线，发生水平向整体屈曲后轴力—屈曲幅值曲线会出现一段轴力随幅值增长而降低的下降段，而缺陷v0/L0较大的管线则不存在下降段，图1为渤海某工程管线处于三种不同大小缺陷状态下管线发生水平向整体屈曲后的轴力—屈曲幅值曲线，采用了Taylor和Gan推导的一阶水平向整体屈曲的轴力公式进行了计算[2]。

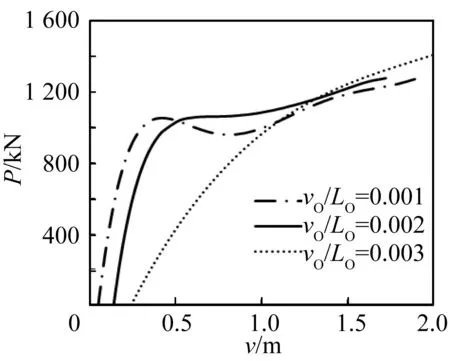
图1 不同幅值与波长比下管线的轴力—屈曲幅值曲线Fig. 1 Axial force vs. buckling amplitude of pipelines with various imperfection ratios

由此可见，初始缺陷大小的确定，不仅影响管线发生整体屈曲的临界荷载，而且严重影响管线在后屈曲阶段的应力和应变，对分析结果的可靠性将会产生很大的影响。

在实际的海底管线工程中，初始缺陷的存在不可避免，可以将管线的初始缺陷分为制造缺陷和铺设缺陷两大类，其中铺设缺陷可分为由于海床的崎岖不平造成的缺陷和人为设置的缺陷。制造缺陷是指管线制造过程中，因制造工艺等因素造成的管线初始挠度、初始椭圆度和初始表面凹陷等，其中管线的初始挠度对水平向整体屈曲分析的意义较大。在已有的规范和资料中，有关管线初始制造缺陷的规定较少，仅DNV-RP-C202中提及管线的缺陷可参照DNV-OS-C401-2013《离岸结构部件的制造和测试》中的相关叙述，根据OS-C401管线的初始挠度幅值和波长比应不大于1.5‰，即对于不考虑铺设缺陷的管线，初始缺陷幅值与波长之比应小于等于1.5‰[18]。随着海洋石油工程向更深海域的发展，管线承受更大的温差和压差，管线内因此产生更大的附加应力，这对管线系统的安全和稳定极为不利。目前越来越多的工程中都采取了在一部分管段人为地设置一定的初始缺陷，以主动触发管线的水平向整体屈曲来释放累积的附加应力。人为因素和多变的海底地质条件使得管线的铺设缺陷具有相当大的不确定性，铺设缺陷大小的确定需要根据具体的实际工程资料和初期设计来确定(在现有研究中，初始缺陷的幅值取值从0.01～2 m甚至更大)，而在不考虑铺设因素的水平向整体屈曲分析时，应将引入缺陷的v0/L0控制在1.5‰以下较为合理。

2 海底管线是否发生水平向整体屈曲的判定

温压联合作用造成的管线内附加应力会使不埋管线有发生水平向整体屈曲的可能性，但何时、何处发生水平向整体屈曲与管线所受的荷载大小、初始缺陷位置和大小、管线所受土体约束力大小有关。在管线设计中，确定管线的屈曲临界荷载，对判断管线在工作荷载下是否发生水平向整体屈曲有着重要的意义。

2.1DNV规范中管线整体屈曲判断标准

2.1.1 DNV《杆件、桁架和球形壳的屈曲强度》规范推荐的方法

对于大长细比结构物的整体屈曲判断，DNV给出了相应的设计规范。早期DNV规范判断管线是否发生整体屈曲时采用的是DNV Classification Notes No.30.1-2004《杆件、桁架和球形壳的屈曲强度》规范推荐的方法，首先根据屈服强度与欧拉屈曲强度之比求出结构物的稳定性强度系数λ[19]：

式中：σE为欧拉屈曲强度，σE=π2E/λk2，λk为柔度，λk=kL/i。

而后根据结构类型的不同，将λ与对应的结构物临界稳定性强度系数λ0进行比较，按下式计算出临界屈曲应力σacr：

式中：μ=θ(λ-λ0)，系数θ取0.5。

当在外荷载作用下，结构物内的最大应力超过σacr时可判定结构物发生整体屈曲。

2.1.2 DNV《壳体的抗屈曲强度》推荐的方法

随着海洋工程的发展，挪威船级社(DNV)针对海洋工程中壳体结构的屈曲稳定性设计，编写出版了DNV-RP-C202《壳体的抗屈曲强度》，可用于验算结构物内外存在压差时的整体屈曲稳定性[20]。《壳体的抗屈曲强度》在验算整体屈曲时，将荷载分为轴向拉(压)力、弯矩、环向压(张)力、扭转力、剪切力五类，考虑截面尺寸、材料特性和所受主导荷载的差异，当管线的长度与截面刚度满足(kL/i)2≥2.5E/σy时需要进行管线的整体屈曲稳定性验算[21]。验算时，首先依据管线所受荷载情况求出管线的轴向压缩应力σa和轴向整体屈曲强度设计值fkcd，计算如下：

式中：γM为材料系数，取1.15；fkc为圆柱整体屈曲强度特征值。

其次，计算环向压差应力σh、弯曲应力σm和管线的局部屈曲强度设计值fakd：

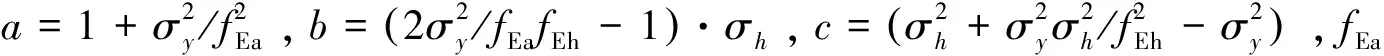
最后，将上述计算值代入式(8)中：

若不等式成立则在该工作荷载组合下管线不会发生整体屈曲。

2.2工程算例

以渤海某工程为背景，管线设计参数如表1所示。分别对理想管线和具有初始缺陷的管线计算整体屈曲临界荷载，进而对比不同计算方法所得结果的差异。

表1 管线设计参数Tab. 1 Design parameters of pipeline

2.2.1 理想管线的临界屈曲荷载

分别采用解析法、规范法和有限元法进行计算，管线的计算长度从10 m 增加到250 m，以2 m为间隔，得到了不同管线计算长度与临界屈曲荷载的关系曲线，如图2所示。其中解析解算法采用了Hobbs在1984年推导的水平向一阶模态的经典解，规范法分别采用了DNV的两种方法，有限元法则采用ABAQUS中的Buckle分析步，该分析步常用来分析刚性结构的分叉荷载，可用于估算理想结构发生整体屈曲时的临界荷载，分析结果在工程的失稳设计中有一定的参考价值。分析中采用C3D8R单元模拟管线，划分网格时管线轴向以0.1 m为间隔划分，每个截面划分8个网格，同时约束屈曲段管线的竖直向位移，对屈曲段以外管线约束全部六个自由度。临界屈曲荷载的有限元计算模型如图3所示。

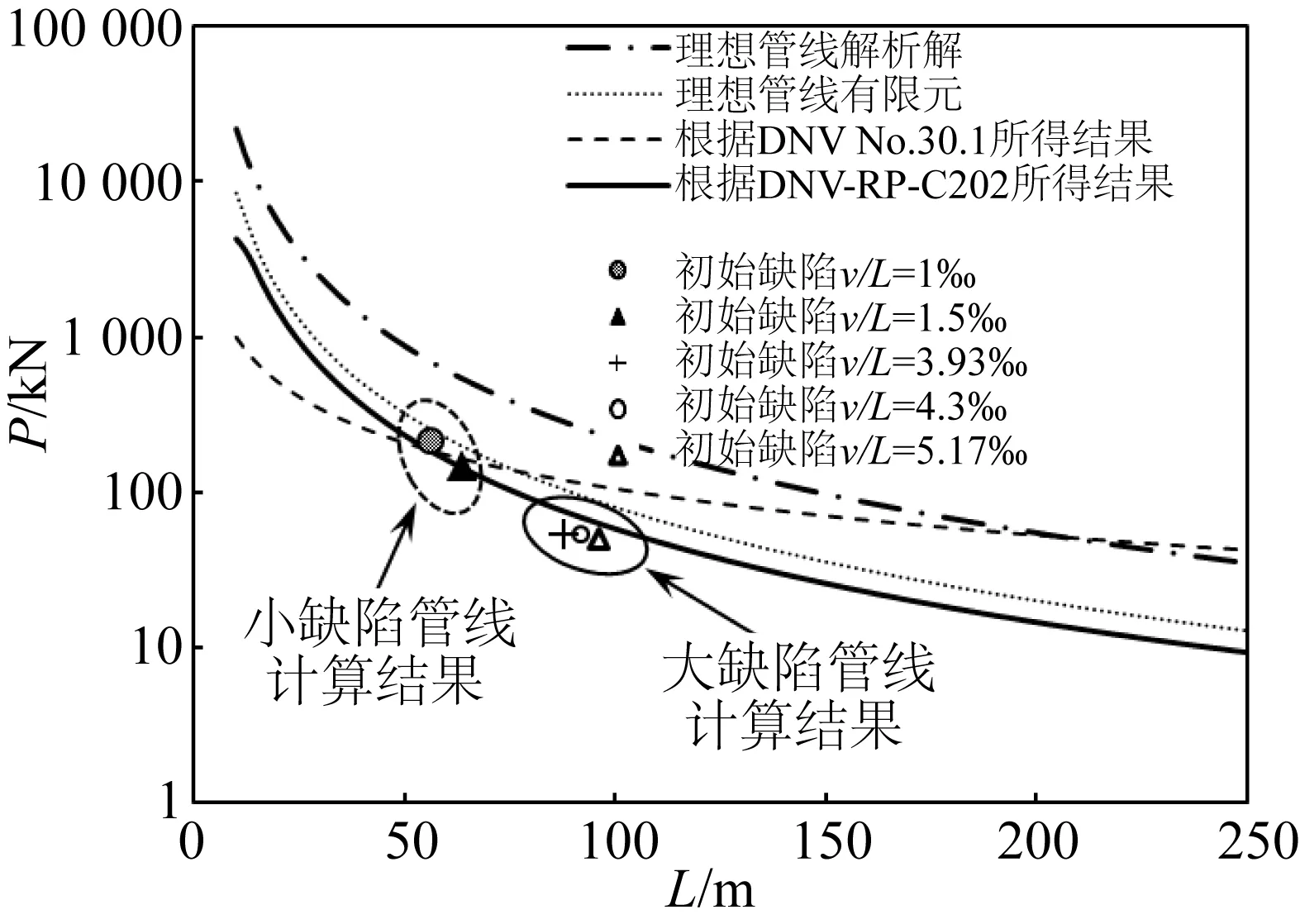
图2 不同屈曲长度管线的临界屈曲荷载Fig. 2 Relationship between critical buckling force and buckling length

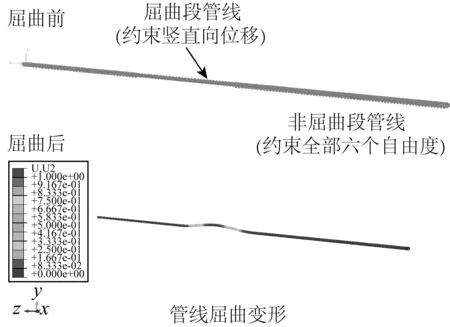
图3 临界屈曲荷载的有限元计算模型Fig. 3 FEA model for critical buckling force calculation

由图2可知，管线的临界屈曲荷载随着整体屈曲长度的增大呈递减趋势，解析解、有限元和DNV-RP-C202的结果曲线递减趋势呈现良好的一致性，而根据DNV Classification Note N0.30.1计算的结果当屈曲长度较小时偏于保守，随着长度增加趋于危险，可见Classification Note N0.30.1对于较短管线具有较高的安全度，随着管线长度的增加，所得结果安全系数下降，不宜用于确定较长管线发生整体屈曲的临界荷载。对比三种方法的计算结果可以看出，解析解结果最大，有限元结果其次，规范RP-C202的结果最小，这是由于解析解基于小挠度理论建立平衡方程求解，而这一理论在小变形分析中精度较高，当变形较大时分析结果存在误差，且没有预留安全系数，因此计算值较大；规范法考虑了制造缺陷限度以内的初始缺陷对管线整体屈曲临界轴力的影响，且预留安全储备，因此计算值最小；有限元法在Buckle分析中忽略了土体约束力，计算值大小介于两者之间，采用非线性算法并进一步细化边界、接触后的有限元模拟可以用于工程中的优化设计。

2.2.2 具有初始缺陷管线的临界屈曲荷载

采用有限元法进行计算，先通过模态引入的方法引入不同大小的初始缺陷[22]，再利用ABAQUS中的动力分析法对缺陷结构进行非线性的后屈曲分析。缺陷状态分为v0/L0≤1.5‰的小缺陷状态和v0/L0>1.5‰的大缺陷状态，缺陷形状以Neil和Gan的研究成果为依据。分别计算了5种不同大小初始缺陷管线的临界屈曲荷载，计算结果如表2与图2所示。

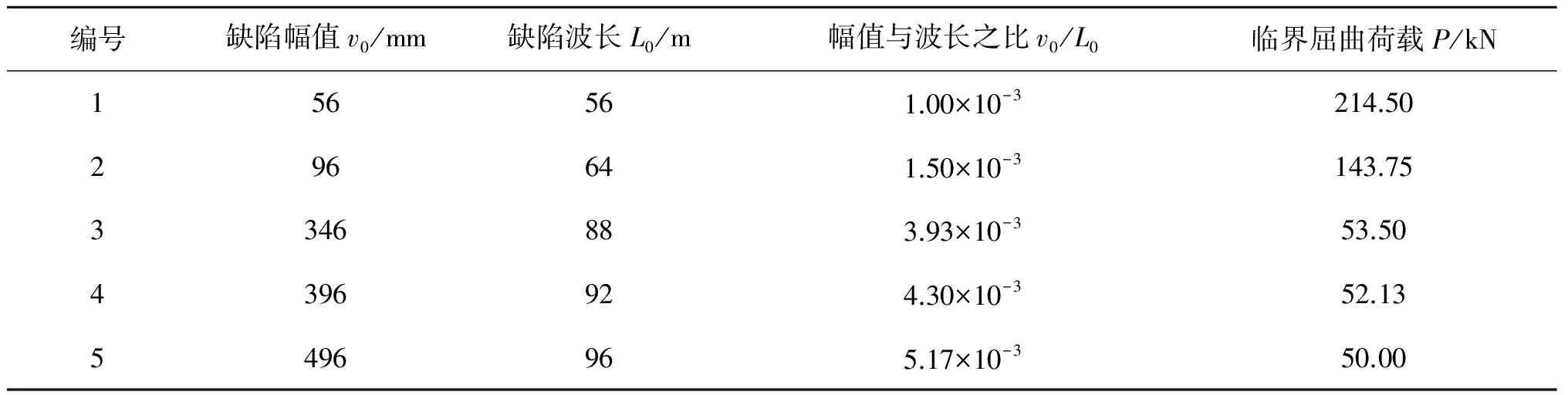
表2 缺陷管线临界屈曲荷载计算值(ABAQUS模拟结果)

对比表2和图2中不同缺陷大小下的管线临界屈曲荷载可知，当缺陷较小不超过制造缺陷上限(v0/L0≤1.5‰)时，某一固定长度下小缺陷管线的临界屈曲荷载介于解析解与规范RP-C202的计算值之间，大缺陷管线的临界屈曲荷载则低于规范RP-C202，即解析解的曲线与规范RP-C202计算所得曲线构成了近平直管线(0‰≤v0/L0≤1.5‰)临界屈曲荷载的值域空间上下限。在实际工程中当近平直管线屈曲长度已知时，若管线所受的实际荷载大于临界屈曲荷载上限值时，可判断管线发生水平向整体屈曲，需要进行下一步水平向整体屈曲的防控设计；若所受的荷载值小于下限值，则不发生整体屈曲，不需要进行水平向整体屈曲的分析。

当缺陷较大超过制造缺陷上限(v0/L0≤1.5‰)时，管线的临界屈曲荷载减小，由图2可知v0/L0=3.93‰、4.3‰、5.17‰的临界屈曲荷载均低于近平直管线值域空间的下限，若实际工程中所受轴力大于规范计算值则管线已经发生水平向整体屈曲，若荷载值低于规范计算值，则需要进一步分析。

将上述方法应用于渤海某工程中判断管线是否发生整体屈曲，假定该工程没有铺设缺陷，按制造缺陷的上限值引入初始缺陷，则缺陷的幅值为96 mm，波长为64 m，管线在正常工作状态下P=EAαT+ApD(0.5-ν)/t/2=3.75 MN，该长度下解析解计算的临界屈曲荷载为0.535 MN，工作荷载值远大于解析解计算值，可以判断管线已经发生整体屈曲，需要进一步进行整体屈曲分析。

3 水平向整体屈曲的破坏标准

判断管线在发生水平向整体屈曲后是否失效至关重要。通常，发生整体屈曲的管线随着温度和内压的增加将进一步产生较大的侧向变形，内部应力随着增长，因此管线是否失效的判断标准也可分为内力判断标准和变形判断标准两大类。

3.1内力判断标准

管线在发生水平向整体屈曲后，伴随着轴力的释放会产生由变形引起的弯矩，过大的弯矩将会对管线系统的安全构成威胁，因此在内力校核时应依照截面轴力与弯矩的组合来进行验算。DNV规范以管线变形最剧烈的截面是否产生局部破坏时荷载组合的临界值作为判断依据[23]。验算时，首先需要计算屈服应力系数αc和管线的等效屈服力Sp、等效屈服弯矩Mp，具体计算如下：

式中：系数β=(60-D/t)/90；fy为设计屈服强度，fy=σy-fy,temp，fy,temp为温度作用下屈服强度的折减值；fu为设计抗拉强度，fu=σu-fu,temp，fu,temp为温度作用下抗拉强度的折减值。

而后，依据管线内外压力的大小分别按式(12)、(13)进行验算，若满足式(12)、(13)，则屈曲后的管线未破坏。

当管线受到的内部压力大于外部压力时：

当管线受到的内压小于外压时：

式中：pc为压溃压强。

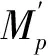
式中：αpm为塑性抗弯系数，αpm=1-DR/(130tRy)，R为作用点的反力，Ry=3.9fyt2。

3.2变形判断标准

发生水平向整体屈曲后，管线产生的压缩应变对管线的安全有重大影响，必须对其进行限定。DNV规范中根据管线内外压力的大小分别进行验算。当管线内压大于外压时，需要考虑压差与破裂压强pb的相互关系，发生水平向整体屈曲后管线截面最大压缩应变ε不应超过压缩应变设计值εRD，验算如下：

式中：γε为安全系数；pmin为管线内所能维持的最小内部压强；αh为应变硬化指数，取0.93；αgw为焊接系数，取1.0。

当管线所受的工作内压小于外部压强时，则考虑压差与管线压溃压强pc的关系，需满足以下条件：

3.3工程算例

采用前述工程算例，运用解析法和有限元法，计算工作荷载下管线发生水平向整体屈曲后管线最危险截面处的轴力、弯矩和应变，分别按照变形、内力判断标准判断管线是否失效。

3.3.1 管线屈曲后内力的计算

解析解法采用王秀妍[24]推导的公式计算管线整体屈曲后的轴力和弯矩，具有初始缺陷的管线发生高阶水平向整体屈曲时，温度荷载与屈曲长度间有如下的对应关系：

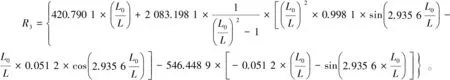
算得对应的屈曲长度后，根据轴力、弯矩与计算长度的关系式，求得屈曲后管线最危险截面处内壁的轴力与弯矩：

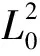
有限元法采用ABAQUS的Explicit算法模拟管线的整体屈曲过程，计算中管线长度取为1 km，在管线中点处引入初始缺陷，管线单元采用Pipe31，土体单元采用C3D8R，管线两端约束水平向和轴向的位移，模拟中土体约束力模型如图4所示。由于ABAQUS中默认的切向摩擦行为为单一摩擦系数的罚函数接触，不能很好的模拟土体对管线的约束，因此对约束模型进行二次开发，通过编译子程序VFRIC引入图4所示的模型作为管土间切向约束关系的控制函数。建立的有限元分析模型如图5所示。

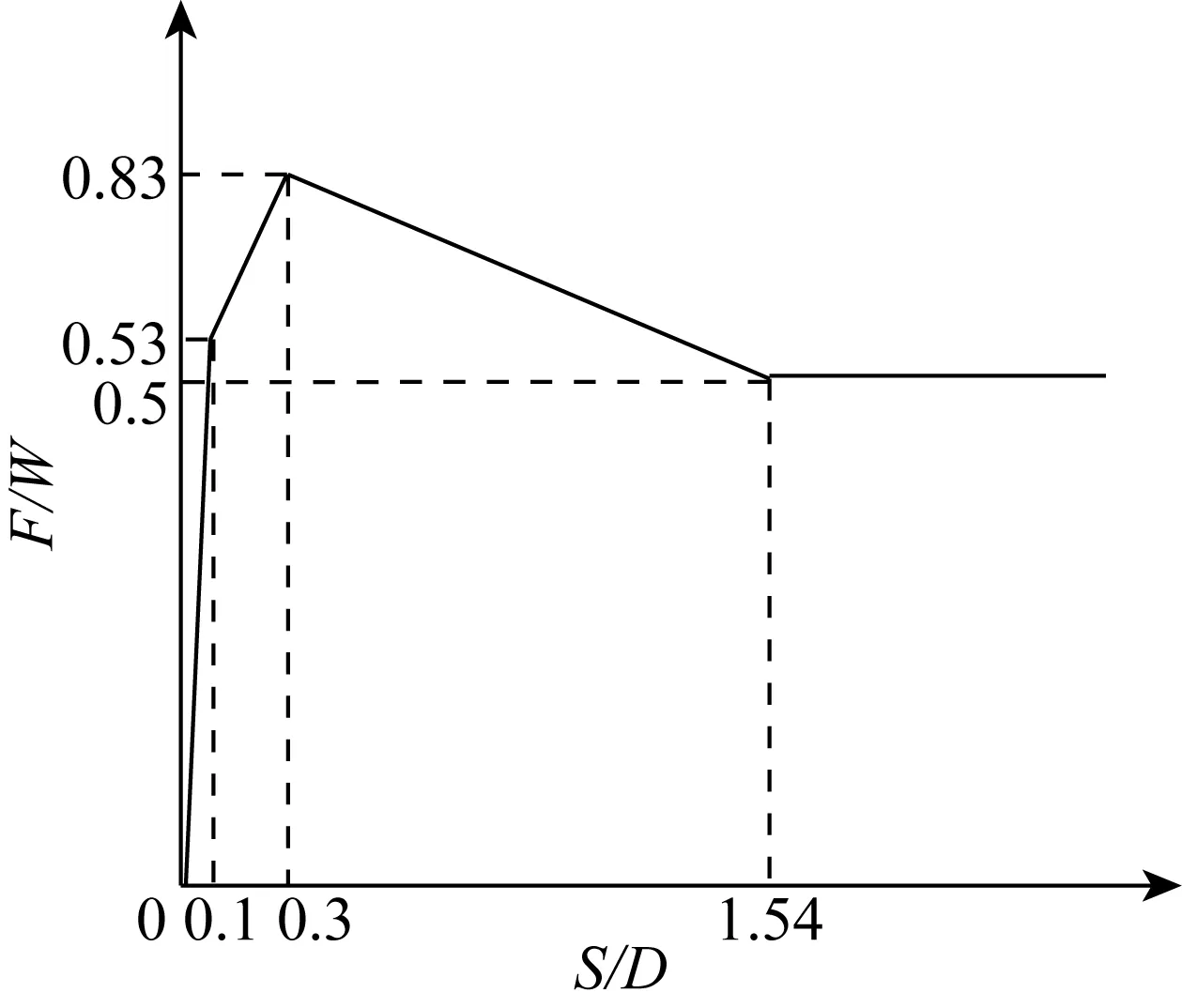
图4 土体约束力模型Fig. 4 Pipe-soil interaction model used in FEA

图5 有限元分析模型示意Fig. 5 FEA model

整体屈曲后管线的轴力云图如图6所示，轴力以拉力为正、压力为负。

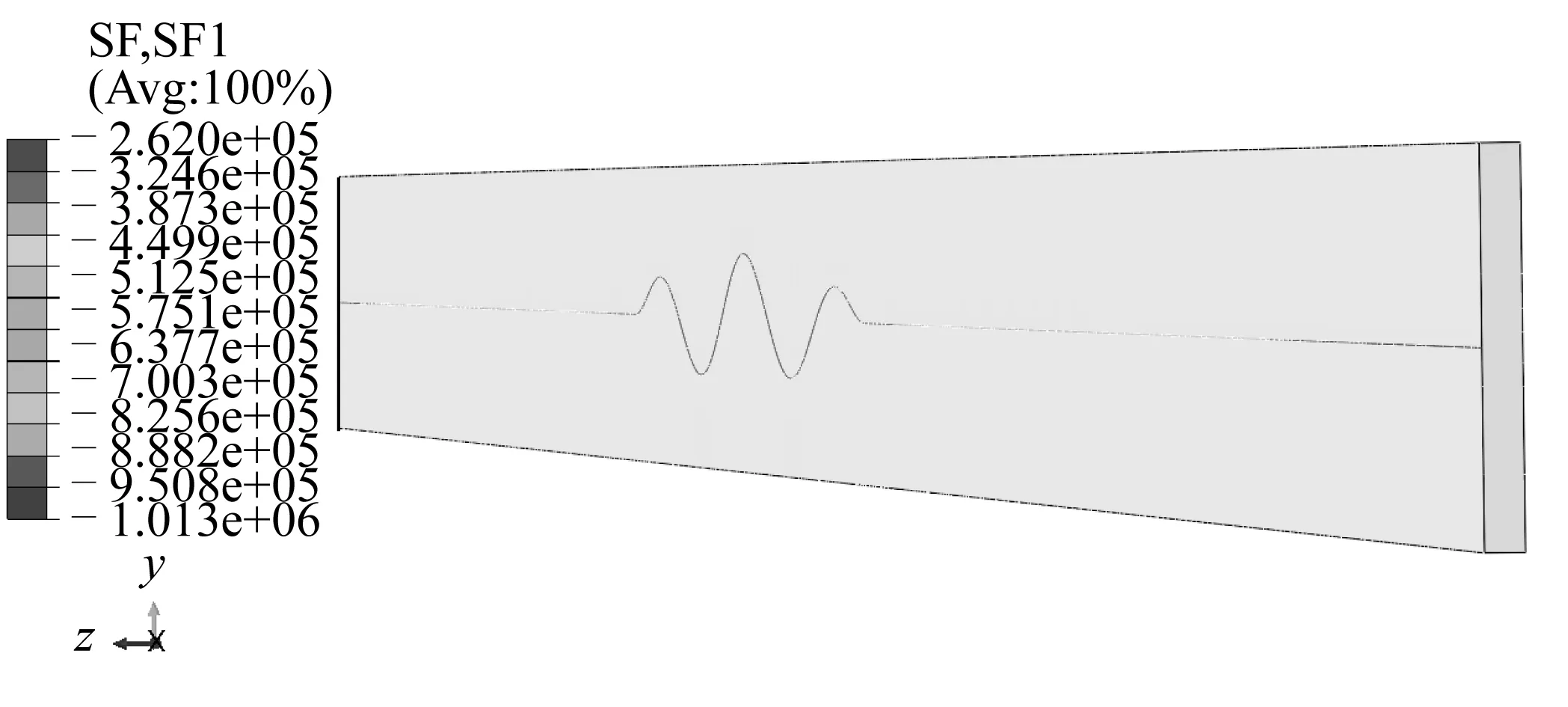
图6 整体屈曲后管线内壁的轴力云图Fig. 6 Contour plot of the axial force in the pipeline

由图6可知，在温度荷载作用下管线全段受压，屈曲段管线由于发生了整体屈曲变形，释放了部分压力，中点处轴力为0.262 MN。

整体屈曲后管线的弯矩云图如图7所示。

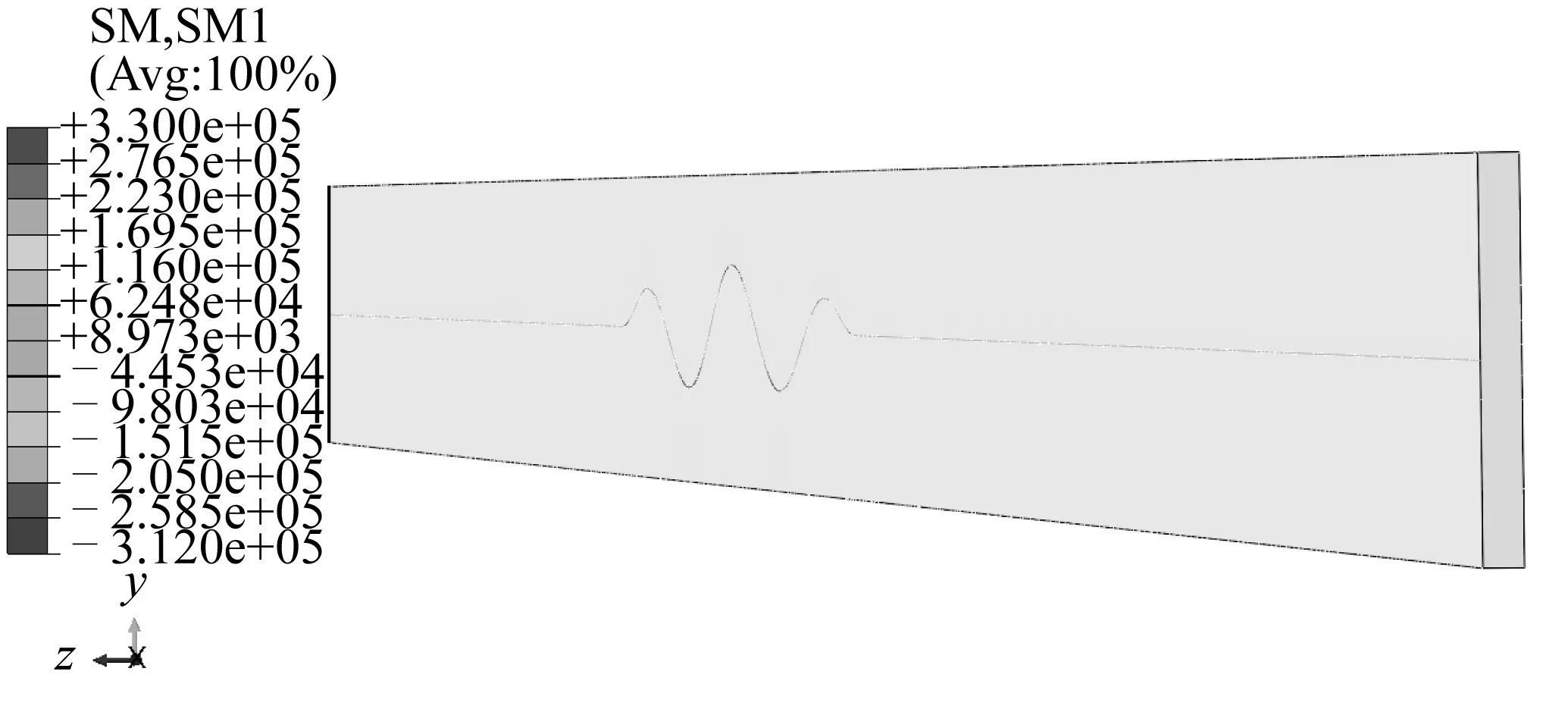
图7 整体屈曲后管线内壁的弯矩云图Fig. 7 Distribution of bending moment in the pipeline

由图7可知，随着变形的发展，管线所受到弯矩增大，最大弯矩出现在管线中点处，为0.33 MNm。

整体屈曲后管线的轴向应变云图如图8所示。

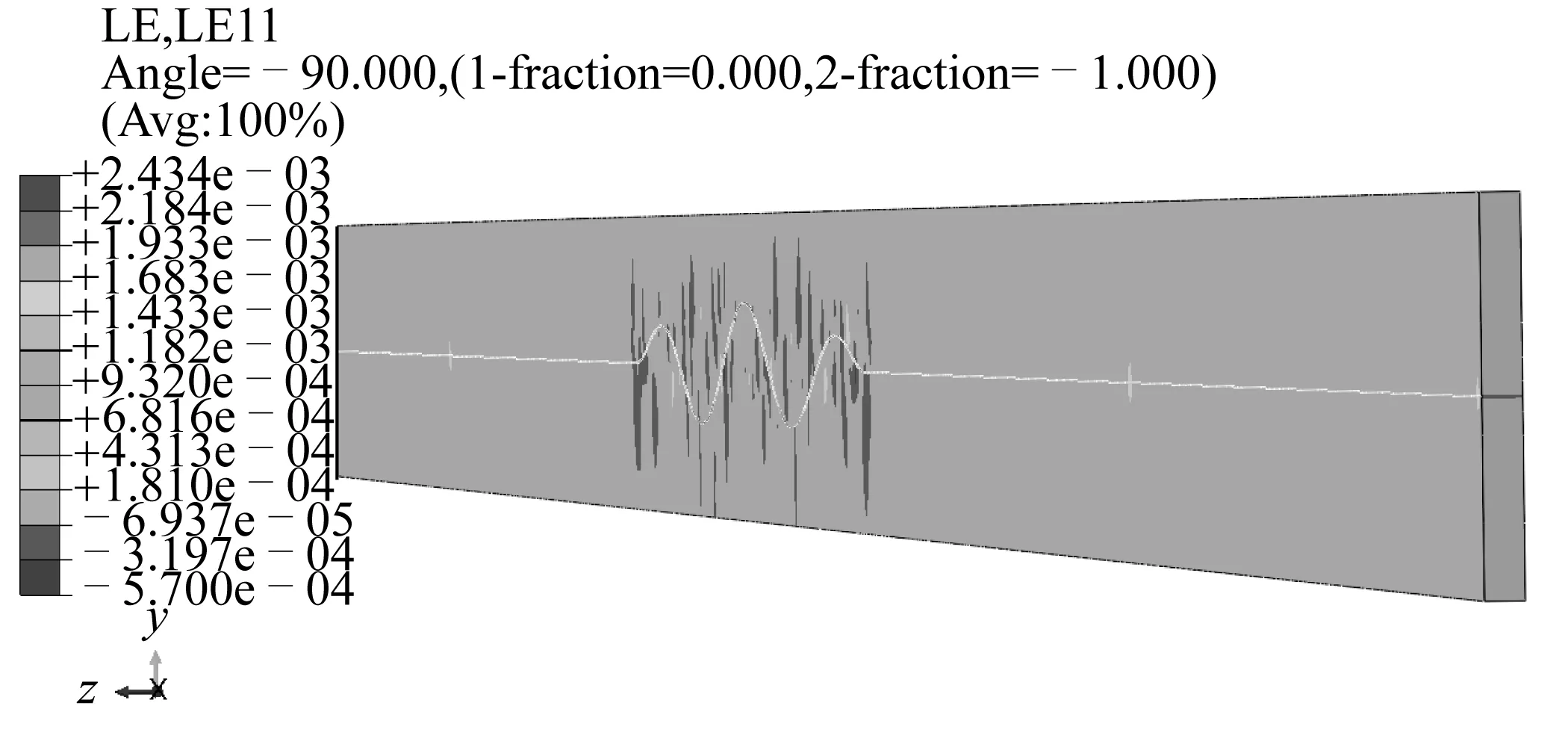
图8 整体屈曲后管线应变云图Fig. 8 Distribution of axial strain in the pipeline

由图8可以看出，轴向应变随变形的增大而增大，最大轴向应变0.243 %。

3.3.2 管线失效判断

按照内力判断标准验算：解析解计算所得最危险截面处的弯矩M=4.05×105N·m、轴力P=1.46×105N，代入式(13)中，可得公式左边为0.626<1满足内力验算标准，管线屈曲后未破坏。有限元法所得最危险截面处的弯矩M=3.33×105N·m、轴力P=2.62×105N，代入式(12)中，得公式左边等于0.423<1满足内力判断标准，管线屈曲后未破坏。

按照变形判断标准验算：有限元法可得到管线的最大压缩应变ε为0.244%，代入式(15)中，得到ε=0.244%<εRD=2.2%满足变形判断标准，管线屈曲后未破坏。

3.3.3 判断标准的讨论

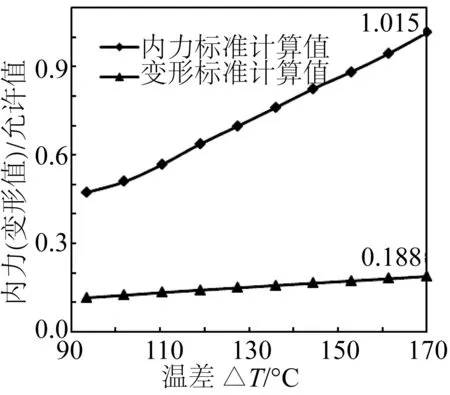
图9 内力判断与变形判断标准的比较Fig. 9 Comparison of two different critical failures

为探究内力判断与变形判断两种标准在工程应用中哪种更为严格，采用继续增加管线温度荷载的方法进行进一步分析，结果如图9所示。图中横坐标代表所受的实际温度荷载值，纵坐标为实际应力、应变与极限应力、应变之比。

从图9中可以看出，随着温度继续上升，截面内力增加显著，而最大压缩应变增加较为缓慢，当工作温差加到170℃时，最危险截面处的弯矩M=5.17×105N·m、轴力P=2.39×105N，代入式(13)中得公式左边等于1.02>1，管线不满足内力验算标准，而此时管线最大压缩应变仅为0.413 %，尚未达到变形标准破坏临界值，因此，相较于变形标准，内力标准在由温压联合作用引起的水平向整体屈曲的校核中更为严格，安全性更高，应作为校核由初始缺陷激发的管线水平向整体屈曲后截面是否发生破坏的主要参照标准。

4 结 语

基于国内外相关领域研究成果，结合工程算例，对海底管线在高温高压作用下是否发生水平向整体屈曲与整体屈曲后管线是否破坏进行了分析，具体结论如下：

1)基于渤海某工程设计参数，运用解析法、规范法和有限元法分析不同缺陷大小对管线临界屈曲荷载的影响，结果显示管线临界屈曲荷载随计算长度的增加而降低、随初始缺陷的增大而降低，且对于理想管线和初始缺陷v0/L0≤1.5‰的小缺陷管线临界屈曲荷载介于规范值和解析解值之间；

2)结合工程实例分别采用内力与变形的判断标准对管线屈曲变形后是否失效进行了验算，并通过进一步分析对比指出了两种验算标准的差异。分析指出由初始缺陷激发的管线发生水平向整体屈曲后截面的破坏验算中，内力验算标准更为严格，应作为主要参照标准。

[1] HOBBS R E. In-service buckling of heated pipelines[J]. Journal of Transportation Engineering, 1984, 110(2): 175-189.

[2] TAYLOR N, GAN A B. Submarine pipeline buckling—imperfection studies[J]. Thin-Walled Structures, 1986, 4(4): 295-323.

[3] KOUNK I, YU S. Continuum FE modeling of lateral buckling: study of soil effects[C]//Proceedings of 26th International Conference on Offshore Mechanics and Arctic Engineering. American Society of Mechanical Engineers, 2007: 347-354.

[4] WANG D, WHITE D J, RANDOLPH M F. Large-deformation finite element analysis of pipe penetration and large-amplitude lateral displacement[J]. Canadian Geotechnical Journal, 2010, 47(8): 842-856.

[5] BRENNODDEN H, SVEGGEN O, WAGNER D A, et al. Full-scale pipe-soil interaction tests[C]//Proceedings of Offshore Technology Conference. 1986.

[6] BRUTON D A S, WHIhite D J, CHEUK C Y, et al. Pipe-soil interaction behaviour during lateral buckling[J]. SPE Projects Facilities & Construction, 2006, 1(3): 1-9.

[7] 刘润, 闫澍旺， 王洪播， 等. 砂土对埋设管线约束作用的模型试验研究[J]. 岩土工程学报, 2011, 33(4): 559-565.(LIU Run, YAN Shuwang, WANG Hongbo, et al. Model tests on soil restraint to pipelines buried in sand[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(4): 559-565.(in Chinese))

[8] LIU R, YAN S, WU X. Model test studies on soil restraint to pipeline buried in Bohai soft clay[J]. Journal of Pipeline Systems Engineering and Practice, 2012, 4(1): 49-56.

[9] BRANSBY M F, NEWSON T A, BRUNNING P. Centrifuge modelling of the upheaval capacity of pipelines in liquefied clay[C]//ISOPE 2002. 2002.

[10] CHEUK C Y, TAKE W A, BOLTON M D, et al. Soil restraint on buckling oil and gas pipelines buried in lumpy clay fill[J]. Engineering Structures, 2007, 29(6): 973-982.

[11] 任艳荣. Abaqus软件在管土相互作用中的应用[J]. 中国海洋平台, 2007, 22(4): 48-51. (RENG Yanrong. The application of ABAQUS software in the pipe/ soil interaction[J]. China Offshore Platform, 2007, 22(4): 48-51.(in Chinese))

[12] JUKES P, ELTAHER A, SUN J. The latest developments in the design and simulation of deepwater subsea oil and gas pipelines using FEA[C]//Proceedings of Third ISOPE International Deep-Ocean Technology Symposium. International Society of Offshore and Polar Engineers, 2009.

[13] PIKE K, DUAN G, SUN J, et al. Comprehensive FEA of thermal mitigation buoyancy module (TMBM)-soil interaction using the coupled eulerian-lagrangian (CEL) method[C]//Proceedings of 29th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, 2010: 865-870.

[14] BRUTON D A S, DAVID J W. Pipe-soil interaction during lateral buckling and pipeline walking-the safebuck jip[C]//Proceedings of Offshore Technology Conference. 2008.

[15] SUN J, JUKES P. From installation to operation: a full-scale finite element modeling of deep-water pipe-in-pipe system[C]//Proceedings of 28th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, 2009: 439-446.

[16] CHEE K Y, WALKER A. Assessment of numerical modelling of pipeline lateral buckling[C]// SUT Symposium of Lateral Buckling. 2011.

[17] LIU R, YAN S. Brief history of upheaval buckling studies for subsea buried pipeline[J]. Journal of Pipeline Systems Engineering and Practice, 2012, 4(3): 170-183.

[18] DNV-OS-C401, Fabrication and testing of offshore structures[S]. Det Norske Veritas, 2013: 47-49.

[19] DNV Classification Notes No.30.1, Buckling strength analysis of bars and frames, and speherical shells[S]. Det Norske Veritas, 2004.

[20] DNV-OS-C101, Design of offshore steel structures, general (LRFD method) [S]. Det Norske Veritas, 2011.

[21] DNV-RP-C202, Buckling strength of shells[S]. Det Norske Veritas, 2013.

[22] LIU R, XIONG H, WU X, et al. Numerical studies on global buckling of subsea pipelines [J]. Ocean Engineering, 2014, 78: 62-72.

[23] DNV-OS-F101, Submarine pipeline systems[S]. Det Norske Veritas, 2012.

[24] 王秀妍. 温压联合作用下海底管线水平向整体屈曲的高阶模态分析[D].天津:天津大学,2013. (WANG Xiuyan. Lateral global buckling high order model analysis of submarine pipeline under HPHT[D]. Tianjin: Tianjin University, 2013. (in Chinese))

Study on submarine pipeline lateral global buckling and buckling failure criterion

LIU Run, HONG Zhaohui, LIU Wenbin

(State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China)

Submarine pipeline is an important way for offshore oil transportation. In operation, pipelines are usually applied under high temperature and high pressure to meet the needs of transport process, and the combined effect of high temperature and high pressure will cause additional stress in pipelines. When the additional stress is greater than the resisting force due to the soil around pipelines, it induces global buckling. Uncontrolled deformation leads to excessive bending which threatens the safety of pipeline system. It is important to ensure that the limit states of pipeline section are not exceeded. This paper analyzes pipeline global buckling with three kinds of methods: analytical method, specification method and numerical method. The critical buckling force of pipelines with different imperfections is calculated and the critical force range is proposed to evaluate the buckling. This study also checks the limit state of a post-buckling pipeline on the basis of the design parameter of a case with Det Norske Veritas codes. The applicability of the criterion load control and that of displacement control is discussed as well. Results show that the load control criterion is stricter than the displacement control criterion.

submarine pipeline; lateral global buckling; critical buckling judgment; post-buckling check

P756.2; TE83

A

10.16483/j.issn.1005-9865.2015.06.001

1005-9865(2015)06-001-09

2014-09-30

国家重点基础研究发展计划(2014CB046800)；国家自然科学基金优秀青年基金(51322904)；高等学校博士学科点专项科研基金资助课题(20130032110074)

刘 润(1972-)，女，教授，博士，博导，主要从事结构物与土的相互作用研究。E-mail: liurun@tju.edu.cn