致密气藏多段压裂水平井非稳态复合产能模型

赵超

（中国石油大学（北京）石油工程教育部重点实验室，北京　102249）

致密气藏多段压裂水平井非稳态复合产能模型

赵超

（中国石油大学（北京）石油工程教育部重点实验室，北京102249）

根据致密气藏压裂后的地质特征，将致密气藏分为压裂区和未压裂区，压裂区为三重孔隙结构，未压裂区为双重孔隙结构；建立了致密气藏多段压裂水平井产能复合计算模型，通过拉普拉斯变换求解得到了多段压裂水平井产能计算公式，绘制了典型无因次产量曲线；通过新旧模型对比，分析了未压裂区对产能的影响，并对相关参数敏感性进行了分析。实例计算表明：流体流动可划分为人工裂缝中线性流动、人工裂缝和压裂区天然裂缝系统双线性流动、压裂区基质系统单线性流动、未压裂区基质和裂缝双线性流动、未压裂区基质控制线性流动、边界控制流动等6个阶段；无因次产量qD随参数ξ（渗透率比）及η（裂缝导流能力比）减小而增大，参数η值越小，未压裂区基质控制线性流动时间越长，边界流出现时间越晚。

致密气；压裂水平井；三重介质；复合模型；非稳态产能

0　引言

中国致密气资源丰富，开发前景广阔，正处于勘探开发的快速发展阶段［1］。目前，致密气藏天然气产量占中国天然气总年产量的1/5左右，已成为天然气供应的重要来源［2］。由于致密气藏渗透率极低，开发时需进行多段压裂，因此，在压裂区易形成极其复杂的裂缝网络。天然裂缝和人工裂缝具有不同的性质，传统的双重孔隙模型［3］已反映致密气藏压裂后的地质特征。

D.Abdassah等［4］提出了径向流双裂缝三重孔隙模型，该模型由基质和双裂缝系统组成，双裂缝系统又分为高渗透率人工裂缝和低渗透率天然裂缝。J.Dreier［5］发展了D.Abdassah等的三重孔隙模型，考虑基质和天然裂缝间窜流为拟稳态，天然裂缝和人工裂缝间窜流为非稳态。Brown等提出了三线性流模型，认为压裂区由有限导流能力的人工裂缝、天然裂缝和基质块3种连续介质构成［6-12］，但该模型只考虑了压裂区气藏产量，未考虑压裂区以外未压裂区对产量的影响。

本文根据致密气藏压裂后的地质特征，将致密气藏分为压裂区和未压裂区。压裂区为三重孔隙结构，由人工裂缝、储层天然裂缝、基质孔隙构成；未压裂区为双重孔隙结构，由储层天然裂缝、基质孔隙构成。建立了致密气藏多段压裂水平井复合产能模型，获得了模型拉斯空间解析解。通过实例计算，绘制了无因次产量曲线，分析了未压裂区对产能的影响。本研究对致密气藏的开发具有一定的指导意义。

1　物理模型

致密储层多为天然裂缝性储层，经水力压裂改造后，形成复杂的裂缝网络系统。可以将致密储层划分为2个区：一个为压裂区，如图1a所示（LF为水力裂缝间距离，Lf为微裂缝间距离，xe为水平井段长度，ye为油藏宽度），由复杂的裂缝网格（包括天然裂缝和水力压裂裂缝）和基质孔隙三重介质构成；一个为未压裂区，如图1b所示，具有天然裂缝系统和基质孔隙双重介质系统［10］。

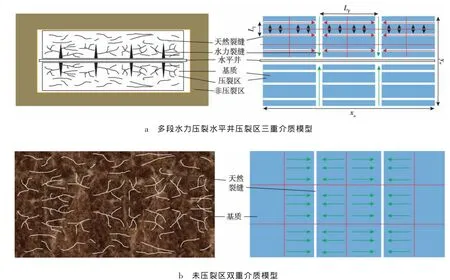
图1　致密储层物理模型

2　数学模型的建立

假设条件：1）致密气藏顶底面封闭、等温等厚，初始条件下地层各处压力相等；2）水平井完全穿透矩形致密气藏，并且在恒定井底流压下生产；3）流动为单相气体流动，且为达西渗流；4）忽略毛细管力和重力的影响，不考虑表皮系数和井筒存储的影响。

根据以上条件，由质量守恒定律可以得到压裂区渗流方程：

根据达西定律，可以得到压裂水平井产量公式：

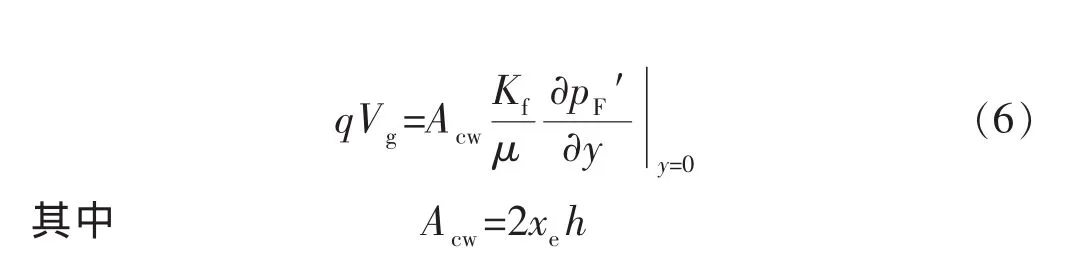
初始条件下，裂缝系统和基质系统处拟压力相等：

水平井恒定压力生产，可以得到：

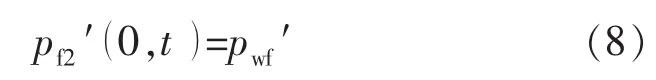
在压裂区和未压裂区界面上，为了满足流体连续性，可以得到：

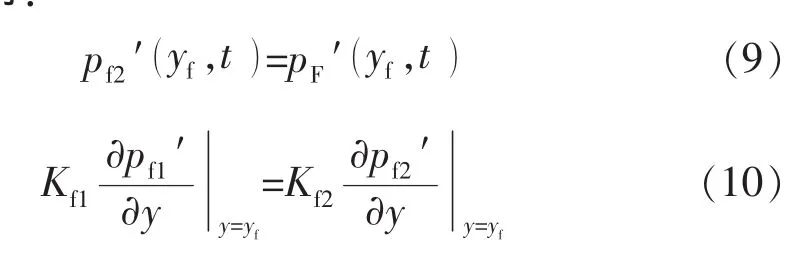
在封闭边界处，可以得到：

将式（1）—（5）无因次化可得：

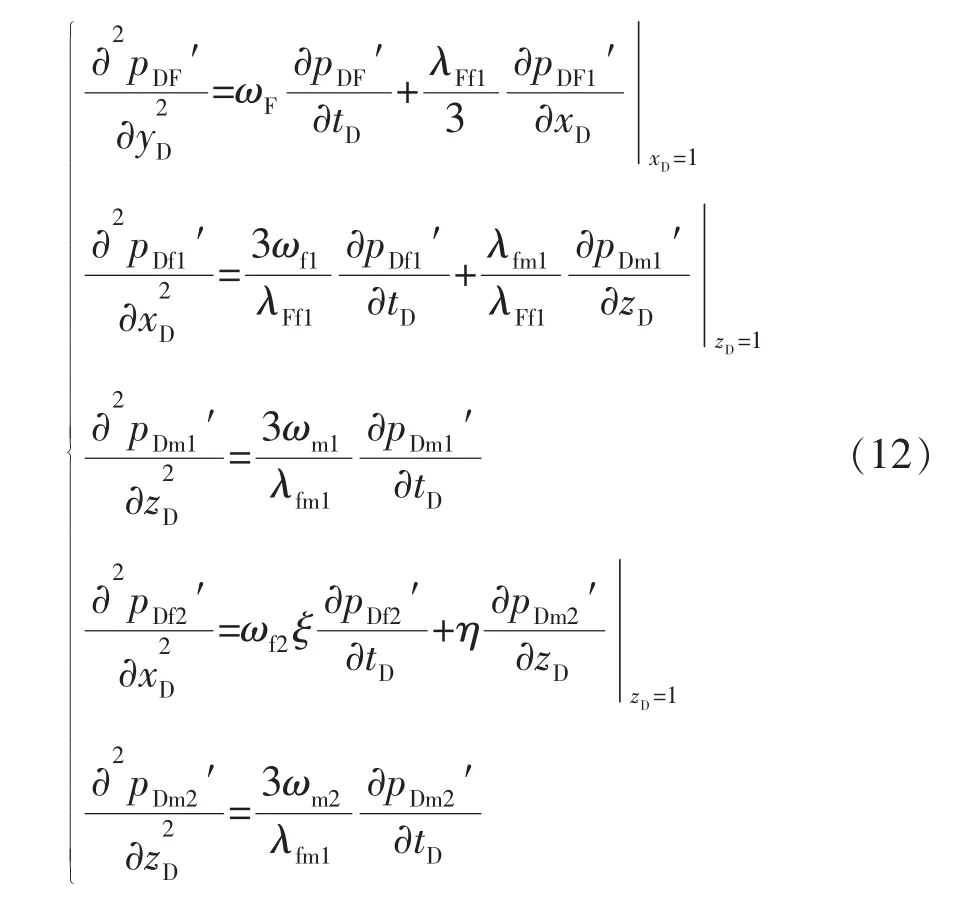
初始条件：

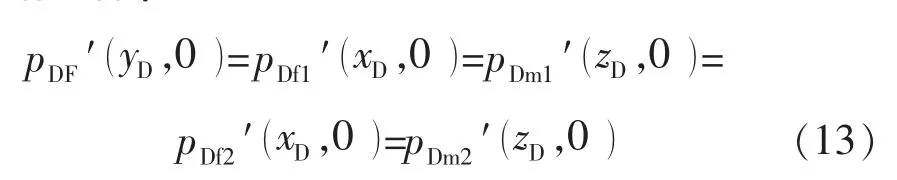
内边界条件：

内外区接触面上的条件：

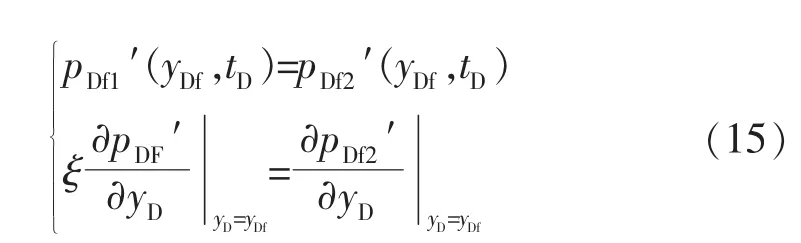
外边界条件：

压裂水平井无因次产量公式：

经过Laplace变换后，得到Laplace空间下的无因次气井产量为

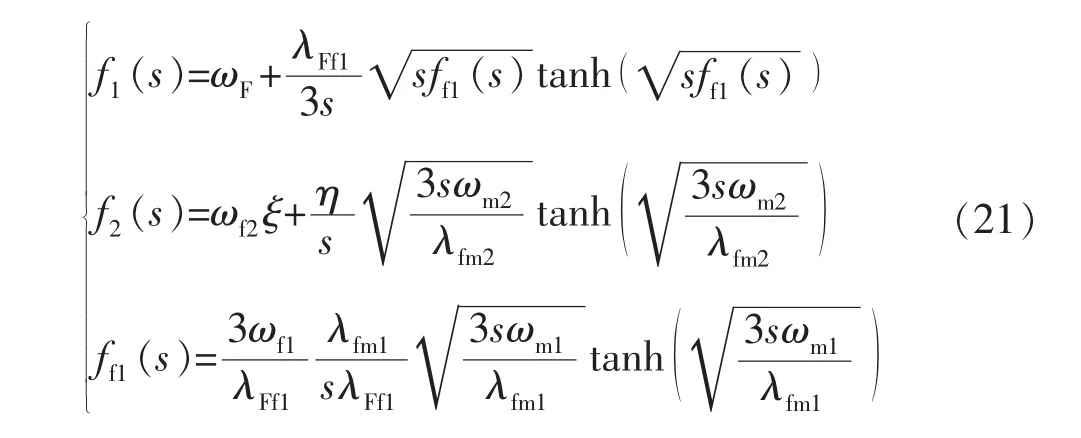
3　实例计算及分析

为了研究未压裂区对致密气藏产能的影响，取西部某致密气多段压裂水平井数据作为基本数据进行产量预测和分析。

基本参数：气藏原始压力31.18 MPa，温度108℃；该压力温度下，气体黏度0.021 mPa·s，气体偏差因子1.02，基质系统孔隙度0.078，天然裂缝系统孔隙度0.008，总压缩系数0.017 64 MPa-1；气藏厚度10 m，气藏宽度10 000 m；水平井段长度1 000 m，水力裂缝间距200 m，天然裂缝间距20 m，裂缝半长100 m；基质系统渗透率Km1=Km2=0.01×10-3μm2，天然裂缝系统渗透率Kf1=Kf2=50.00×10-3μm2，水力裂缝渗透率50 μm2；基质与微裂缝间窜流系数λfm1=λfm2=10-6，天然裂缝向水力裂缝的无因次窜流系数λFf=100；水力裂缝储容比0.000 1，压裂区天然裂缝储容比0.000 1，压裂区基质储容比ωm1=1-ωf1-ωF，未压裂天然裂缝储容比0.01，未压裂区基质储容比0.99；渗透率比10；导流能力比0.33×10-6；井底流压28.18 MPa。

从式（18）可知，ξ和η对致密气井产能具有重大影响。本文在其他基本参数不变、分别给定不同的ξ和η的情况下，研究了参数ξ和η对致密气井产能影响。

3.1非稳态无因次产量曲线

根据式（18），采用stehfest数值反演方法计算得到实空间无因次产量变化曲线（见图2）。

图2　无因次产量曲线

由图2可以看出，无因次产量曲线可分为6个流动阶段：1）人工裂缝中线性流动，产能曲线斜率为-1/ 2。这是由于水力裂缝的高导流能力，该阶段产能高且下降很快。2）人工裂缝和天然裂缝中双线性流动，斜率为-1/4。3）基质中单线性流动，斜率为-1/2。4）外部未压裂区基质和裂缝双线性流，产量与时间的双对数曲线斜率为-1/4。5）外部为压裂区基质控制的线性流动，斜率为-1/2。这是由于未压裂区与压裂区相比范围更大，且压力波在基质中传播较慢，持续时间长。6）最后压力传播到外部封闭边界，为封闭边界控制的流动，气井产能快速下降。

3.2无因次产量曲线对比

为了更好地分析未压裂区对产能曲线的重要性，将新的复合模型计算结果与只考虑压裂区的旧模型产能曲线进行比较。采用3.1的基本参数计算得到新、旧模型无因次产量曲线（见图3）。从图可以看出：在生产早期，新、旧模型无因次产量曲线几乎重合（主要原因是，这时流动主要受到压裂区控制，外部未压裂区对产量影响不明显）；随着生产时间增加，未压裂区地层对致密气井产能产生影响，新模型与旧模型无因次产量曲线差别较大；当生产到达一定时间（到达边界流）后，新、旧模型产量曲线形态基本相同，复合模型无因次产量曲线稍高。

图3　新、旧模型无因次产量对比

3.3渗透率比ξ对产能的影响

图4为参数ξ不同值时的新模型无因次产量曲线。

图4　不同ξ值时新模型的无因次产量曲线

由图4可知：参数ξ对前期产能曲线没有影响，而对中后期产能曲线有明显影响，ξ值越小，致密气井无因次产量越大。主要原因是，较小的ξ值意味着较大的未压裂区渗透率。

3.4导流能力比η对产能的影响

图5为不同η值时新模型的无因次产量曲线。

图5　不同η值时新模型的无因次产量曲线

由图5可知：参数η对前期产能曲线仍然没有影响，而对中后期产能曲线有明显影响，η值越小，无因次产量值越大；随着η减小，由未压裂区基质控制的线性流动时间延迟，致密气藏外边界对流动开始产生影响的时间延迟。

4　符号注释

p′，pi′分别为地层拟压力和初始条件下的地层拟压力，MPa2/（mPa·s）；μ为气体黏度，mPa·s；φ为孔隙度，%；Ct为综合压缩系数，MPa-1；K为渗透率，μm2；t为时间，h；x，y，z为空间坐标，m；q为流量（产量），m3/d；Vg为气体体积系数；Acw为泄气面积，m2；xe为水平井段长度，m；h为气藏厚度，m；yDe为无因次长度；yDf为水力裂缝无因次半长；ω为储容比；λFf1为压裂区天然裂缝向水力裂缝的无因次窜流系数；λfm1，λfm2分别为压裂区和未压裂区基质向天然裂缝的无因次窜流系数；η为裂缝导流能力比；ξ为渗透率比；T为气藏温度，K；s为Laplace变量。下标：F为人工裂缝；f1，f2分别为压裂区和未压裂区天然裂缝；m1，m2分别为压裂区和未压裂区基质系统；t为各介质的总和；sc为标准状态；D为无因次。

5　结论

1）建立了致密气藏多段压裂水平井复合产能模型，对模型进行了求解；绘制了致密气井无因次产量曲线，并根据产量公式进行了参数敏感性分析。

2）致密气藏流体流动可分为6个流动阶段：人工裂缝中线性流动、人工裂缝和压裂区天然裂缝系统双线性流动、压裂区基质系统单线性流动、未压裂区基质和裂缝双线性流动、未压裂区基质控制线性流动和边界控制流动。

3）致密气井产能生产前期不受渗透率比ξ和导流能力比η的影响，而生产中后期，参数ξ和η对致密气井产能曲线具有重大影响。

［1］李建忠，郭彬程，郑民，等.中国致密砂岩气主要类型、地质特征与资源潜力［J］.天然气地球科学，2012，23（4）：607-615.

［2］康毅力，罗平亚.中国致密砂岩气藏勘探开发关键工程技术现状与展望［J］.石油勘探与开发，2007，34（2）：239-245.

［3］Warren J E，Root P J.The behavior of naturally fractured reservoirs［R］.SPE 426，1963.

［4］Abdassah D，Ershaghi I.Triple-porosity systems for representing naturally fractured reservoirs［R］.SPE 13409，1986.

［5］Dreier J.Pressure-transient analysis of wells in reservoirs with a multiple fracture network［R］.SPE 130298，2004.

［6］Brown M L，Ozkan E，Raghavan R S.Practical solutions for pressure transient responses of fractured horizontal wells in unconventional reservoirs［R］.SPE 130368，2009.

［7］Bello R O.Rate transient analysis in shale gas reservoirs with transient linear behavior［D］.Canyon：Texas A&M University，2009．

［8］Al-Ahmadi H A.A triple-porosity model for fractured horizontal wells［D］.Canyon：Texas A&M University，2010.

［9］Tivayanonda V.Comparison of single，double，and triple linear flow modelsforshalegas/oilreservoirs［D］.Canyon：TexasA&MUniversity，2012.

［10］Al-Ahmadi H A，Almarzooq A M，Wattenbarger R A.Application of linear flow analysis to shale gas wells-Field cases［R］.SPE 130370，2010.

［11］段永刚，李建秋.致密气无限导流压裂井压力动态分析［J］.天然气工业，2010，30（3）：26-29.

［12］El-Banbi A H.Analysis of tight gas wells［R］.SPE 124550，1998.

（编辑李宗华）

Transient and compound productivity model for multi-fractured horizontal well in tight gas reservoir

Zhao Chao
（MOE Key Laboratory of Petroleum Engineering，China University of Petroleum，Beijing 102249，China）

Based on the tight gas reservoir geological characteristics after fracturing，the tight gas reservoir is divided into unfractured zone and fractured zone，fractured zone is regarded as the triple medium and unfractured zone is regarded as the dual medium.A new composed productivity calculation model for multi-stage fractured horizontal well in tight gas reservoir has been established to analyze the productivity characteristics of tight gas reservoir.The typical curve of normalized production versus normalized time has been figured and the new model has been compared with the old model to analyze the effects of unfractured zone on the productivity，and the sensibilities of different parameters have also been analyzed.The results show that the fluid flow can be divided into six stages：linear flow in artificial fracture，bilinear flow in natural fracture and fractured zone，single linear flow in matrix system of fractured zone，bilinear flow in matrix and fracture of non-fractured zone，linear flow controlled by the matrix system of non-fractured zone and the boundary flow.Normalized production qDincreases with the decrease of ξ and η.The smaller the parameter value of η is，the later the linear flow time controlled by the matrix system of non-fractured zone is.Meanwhile，the time of the boundary flow delays for the smaller η.

tight gas；fractured horizontal well；triple porosity；compound model；transient productivity

国家科技重大专项“碳酸盐岩油田开发关键技术”课题“复杂介质数值模拟技术与软件”（2011ZX05014-005）；

国家自然科学基金项目“多尺度离散裂缝油藏有限元数值模拟研究”（51204204）

TE319

A

10.6056/dkyqt201505023

2015-03-13；改回日期：2015-07-13。

赵超，男，1990年生，在读硕士研究生，主要从事油气田开发工程方面研究。E-mail：13001284648@163.com。

引用格式：赵超.致密气藏多段压裂水平井非稳态复合产能模型［J］.断块油气田，2015，22（5）：651-655.

Zhao Chao.Transient and compound productivity model for multi-fractured horizontal well in tight gas reservoir［J］.Fault-Block Oil&Gas Field，2015，22（5）：651-655.