基于时频分析的高速运动点目标运动参量挖掘算法

王云良+王敏其

摘 要： 通过对高速运动点目标的运动参量挖掘，实现对高速运动目标的速度、时延、方位等信号源参量的准确估计。传统方法主要采用宽带信号检测方法实现对高速运动点目标的参量挖掘和估计，当运动目标的时频特征具有窄带特性时，对目标运动参量估计精度不高。提出一种基于时频分析的高速运动点目标运动参量挖掘算法，构建高速运动点目标的信号回波模型，采用级联滤波算法对运动目标的干扰特征进行降噪滤波处理，对信号提取四阶累积量时频特征，直接获取近场源的参量，通过时频分析避免了谱峰搜索，减少对运动特征参量的挖掘计算量，提高参量估计精度。仿真结果表明，采用该算法进行高速运动点目标的运动参量挖掘和信号参量估计，能有效实现信号的抗干扰滤波，对运动目标的时延、方位角等参量估计精度较高，展示了较好的应用价值。

关键词： 时频分析； 运动目标； 参量估计； 数据挖掘

中图分类号： TN911.7?34 文献标识码： A 文章编号： 1004?373X（2015）20?0031?04

High?speed moving point?target parameter mining algorithm based on

time?frequency analysis

WANG Yunliang1， WANG Minqi2

（1.Changzhou Institute oF Mechatronic Technology， Changzhou 213164， China； 2. Changzhou Wujin Wuyang Textile Machinery Co.， Ltd， Changzhou 213164， China）

Abstract： The accurate estimation for the speed， time delay and azimuth of high?speed moving target was realized by mining the motion parameters of the target. In view of the deficiency that traditional test method of broadband signal has low accuracy when time?frequency characteristics of the moving target has a narrow band feature， a new motion parameter mining method for high?speed moving point target based on time?frequency analysis is proposed. The echo signal model of high?speed moving point target was established. The denoise filtering processing for interference feature of moving target is carried out with cascade filtering algorithm. The fourth?order cumulant time?frequency characteristics of signals are extracted to obtain near?field source parameters directly， which avoided the spectrum peak search by time?frequency analysis， reduced the mining calculated quantity of motion characteristic parameters and improved the accuracy of parameter estimation. The simulation results show that the new method to excavate the moving target parameters and estimate the signal parameters can realize anti?interference filtering of signals effectively， and has high accuracy in parameter estimation of time?delay， azimuth， etc.

Keywords： time frequency analysis； moving target； parameter estimation； data mining

0 引 言

高速运动点目标的速度和时延估计是实现目标识别和检测的基础。雷达、声纳等目标信号表现为一种高速运动的近场信源点目标信号，为了准确实现对目标的方位估计，提高对运动目标的识别和跟踪打击能力，需要对高速运动的点目标信号进行准确的信号源参量估计。通过对高速运动点目标的运动参量挖掘，实现对高速运动目标的速度、时延、方位等信号源参量的准确估计。相关算法的研究在声纳、通信、雷达等军事领域具有重要的应用前景和价值。通常，高速运动的点目标信号按照一定方式排列在阵列近场源传感器中，通过采样接收空间时域信号完成相关估计。在此过程中，需要采用一定的信号处理算法，通过信号检测和目标参量估计，实现对运动点目标的参量挖掘。类似参量估计和挖掘的主要特征以波达方向（Direction of Arrival，DOA）估计为代表。对高速运动点目标的参量挖掘将限于DOA、距离、频率参数的联合估计，由此实现对声纳、雷达等目标信号的识别和检测[1]。

近年来，对高速运动点目标的参量挖掘方法研究受到了广大学者的关注，提出了许多解决声纳、雷达等目标信号参量估计和数据挖掘问题的方法。传统方法中，对高速运动点目标的参量挖掘方法主要有在时间域上和在频域上进行运动参数挖掘，采用时频分析的数字信号处理方法，通过对运动目标的时频特征提取，实现高速运动点目标运动参量的速度、方位角、时延和频率等参数的估计[2]。其中，文献[3]提出基于多普勒扩散频繁项挖掘的高速运动点目标运动参量估计算法，采用多普勒频率模糊数搜索的方法进行运动目标的参量信号模型构建和参数估计，实现对参量挖掘，拟合值与真实值接近，但是该算法存在计算开销较大，实时性不好的问题；文献[4]提出基于高阶累积量的近场源参量估计的高速运动点目标运动参量挖掘算法，算法的优点在于能抑制高斯噪声（白色或有色）提取非高斯信号，由于在参量估计中均使用二阶统计量进行阵列观测信号的处理，改善了算法对运动特征参量的估计精度。但是该算法采用二维穷尽搜索进行信号的时频分析，当目标出现线性宽带主动脉冲辐射时，估计性能不好[5]。当前方法主要是采用宽带信号检测方法实现对高速运动点目标的参量挖掘和估计，当运动目标的时频特征具有窄带特性时，对目标运动参量估计精度不高。针对上述问题，本文提出一种基于时频分析的高速运动点目标运动参量挖掘算法。首先构建高速运动点目标的信号回波模型，采用级联滤波算法对运动目标的干扰特征进行降噪滤波处理，对信号提取四阶累积量时频特征，直接获取近场源的参量，通过时频分析避免了谱峰搜索，减少对运动特征参量的挖掘计算量。最后通过仿真实验进行了性能验证，以雷达目标信号为实例进行性能对比测试，展示了本文算法在实现高速运动点目标运动参量挖掘和估计中的优越性能，得出了有效性结论。

1 高速运动点目标回波信号模型和干扰滤波

1.1 高速运动点目标回波信号模型构建

高速运动点目标信号常用在声呐、合成孔径雷达等信号检测和目标识别中，为了实现对高速运动点目标的运动参量挖掘，通过对目标运动的时延、方位等参量的准确估计，提高目标识别能力，算法设计的第一步是要进行目标回波模型构建。

通常情况下，高速运动点目标表现为一组阵列信号，待估计信源均匀分布在阵列信号的接收基阵中，假设目标回波信号模型为宽带模型，给定一向量组[x1，x2，…，xn∈Cm]（m维复数空间），以通过信源的DOA和距离参数向量为线性组合的集合，这种线性组合的集合称为由向量组[x1，x2，…，xn]张成的子空间，或称作[x1，x2，…，xn]的张成，由于近场源波前的形状随阵元位置具有非线性变化特性，即有：

[spanx1，x2，…，xn=i=1naixiai∈C] （1）

假定由[N=2P]个阵元组成的等距线阵高速运动点目标回波模型，任意一个[m×n]维矩阵[A]的值域定义为：

[range（A）=y∈Cmy=Ax， if x∈Cn] （2）

如果[A=[a1，a2，…，an]]为一个列分块矩阵，设阵列中心处的阵元坐标为0，接收信号可表示为：

[xm（t）=i=1Isi（t）ejφmi+nm（t），-p+1≤m≤p] （3）

式中：[si（t）]为第[i]个高速运动点目标回波信源的复包络；[xm（t）]为阵元m接收阵列的子空间特征信号；[nm（t）]为加性干扰噪声。噪声分布[p（ekvk）]的方差和均值服从分布如下：[H0： x（t）=w（t）H1： x（t）=Et-∞+∞f（t-λ）bR（λ）dλ+w（t），-∞≤t≤+∞] （4）

高速运动点目标信号中的加性色噪声v（n）可以为高斯分布或非高斯分布，分析上述信号模型可见，目标信号[xn]中只含有一个正弦分量，为：

[x（n）=Acos（0.3πn+φ）+v（n）] （5）

式中：相位[φ]在[-π，π]之间高斯分布，利用向量[W]和[Xk]之间的协方差随机递减特性，可以将目标回波模型的时频特征误差信号[ε（k）]写成：

[ε（k）=d（k）-WTX（k）=d（k）-XT（k）W] （6）

考虑阵元接收到的信源[i]信号的相位差，高速运动点目标回波信号的时延估计误差平方为：

[ε2（k）=d2（k）-2d（k）XT（k）W+WTX（k）XT（k）W] （7）

上式两边取数学期望后，得到[φmi]的解析表达式为：

[φmi=2πriλ1+m2d2ri2-2mdsinθiri-1]

式中：[ri]，[θi]分别为待估计的第[i]个点目标分布阵列的近场源时频特征参量。构建一个未知多重假设检验判决模型，对上式进行泰勒级数展开，得到高速运动点目标信号的速度参量均方误差为：

[Eε2（k）=Ed2（k）-2Ed（k）XT（k）W+WTEX（k）XT（k）W] （8）

通过上述可见，构建的高速运动点目标回波信号模型的运动参量估计由DOA和距离两个参数决定，通过参数估计实现对运动特征参量的挖掘，提高目标识别能力。

1.2 干扰滤波处理

在上述进行的高速运动点目标信号回波模型构建的基础上，通过对信号的时频分析可见，信号受到干扰作用，需要首先进行降噪滤波设计[6]，本文采用级联滤波算法对运动目标的干扰特征进行降噪滤波处理，滤波器的结构原理和实现结构图如图1所示。

图1 级联滤波抗干扰设计

图1中所示的二阶格型陷波器结构框图中[7]，x（k）为观测序列，它是由信号和背景噪声共同构成的，y（k）为除去正弦信号成分后的输入信号，即为噪声信号。陷波器的传输函数为：

[H（z）=1+az-1+z-21+arz-1+r2z-2， 0

当陷波器的陷波频率点落在x（k）中所含正弦信号的频率处，传递函数改进为：

[H（z）=1+sinθ22·1+2sinθ1z-1+z-21+sinθ1（1+sinθ2）z-1+sinθ2z-2] （10）

由于在陷波频率处有：

[H（ejω0）=0] （11）

根据最小均方误差准则，即[Φ（ω0）=π]，于是可以得到：

[ejπ=V（ejω0） =sinθ2+sinθ1（1+sinθ2）ejω0+ej2ω01+sinθ1（1+sinθ2）ejω0+sinθ2ej2ω0=-1] （12）

分别估计前项预测误差或后项预测误差，得到陷波频率为：

[ω0=θ1+π2， θ1<π2] （13）

选取不同的陷波器频率参数[a]和带宽参数[r]所得的幅频响应曲线，通过抗干扰设计，对各组成节点目标信号进行局部优化，当[r→1]时陷波器的带宽减小，同时陷波深度也减小，由此实现抗干扰滤波。

2 时频分析及运动参量挖掘改进实现

上述构建的高速运动点目标的信号回波模型，采用级联滤波算法对运动目标的干扰特征进行降噪滤波处理，针对传统方法采用宽带信号检测方法实现对高速运动点目标的参量挖掘和估计，当运动目标的时频特征具有窄带特性时，对目标运动参量估计精度不高的问题，本文提出一种基于时频分析的高速运动点目标运动参量挖掘算法。算法改进的原理是对信号提取四阶累积量时频特征，直接获取近场源的参量，通过时频分析避免了谱峰搜索，减少对运动特征参量的挖掘计算量。首先定义如下的四阶累积量矩阵，结合高速运动点目标的特征子空间元素，定义的四阶累积矩阵为：

[C1m，n=cumx*m（t），xm+1（t），x*n+1（t），xn（t）] （14）

式中：“*”表示复共轭，对三次特征分解的参数进行配对，推出信号的时频分析结果为：

[P1=（AH2A2）-1AH2A1， P2=（AH3A3）-1AH3A1] （15）

根据[Γ]，[Ψ]，[r]三者的特征分解中特征值和特征向量是时频级联对应关系，若用[C4S]表示由信源峰度组成的对角矩阵，那么高速运动目标的时延特征值为[C4S=diagc4s1，c4s2，…，c4sI]，由于特征值与特征向量的排列次序是随机的，则对于[0≤m，n≤P-1]，有：

[C1=AC4SAH] （16）

式中，[A]是一个维数为[P×I]的矩阵，其第[i]列矢量表示运动目标的频率特征参量：

[ai=1，ej2?i，…，ej2（P-1）?iT] （17）

为了估计信号的频率，计算上述特征矢量组成的酉矩阵，得到高速运动目标的DOA波动向量的到达角和频率的三维联合估计结果，由信号子空间理论可知，采用时频分析算法[7?8]，提高信号的检测精度，由于高速运动点目标的回波信号带宽B远小于其中心频率，那么通过时频分析，得到空间状态累计量矩阵[C2]，其元素[C2m，n]为：

[C2m，n=cumx*m（t+1），xm+1（t），x*n+1（t），xn（t）] （18）

分析回波信号的慢变相位调制函数，在时域数字特征中，计算实信号[x（t）]的方差，提取四阶累积量时频特征，直接获取近场源的参量，参量[Φ，Ω，Λ]的挖掘结果分别为：

[Φ=diag[ej2?1，ej2?2，…，ej2?I]] （19）

[Ω=diag[e-j2γ1，e-j2γ2，…，e-j2γI]] （20）

[Λ=diag[ej2w1，ej2w2，…，ej2wI]] （21）

假设[I]个空间入射信号[si（t）]，对矩阵[C]作特征分解为：

[C=EΣEH] （22）

式中：[E=[e1，e2，…，e4P]]为由特征矢量组成的酉矩阵，由于高速运动点目标入射到接收阵列的近场源数目[I]已知，把[Es]分成4个[P×I]的矩阵[E0]，[Ex]，[Ey]，[Ez]，即：

[Es=[e1，e2，…，eI]=E0ExEyEz] （23）

式中，对角元素与[Λ]的对角元素分别对齐，基于时频分析，采用多普勒频率模糊搜索的方法完成高速运动点目标运动时延信息、速度信息和相位信息等特征的联合估计和挖掘，直接获取近场源的参量，通过时频分析避免了谱峰搜索，减少对运动特征参量的挖掘计算量，提高参量估计精度。

3 仿真实验与性能分析

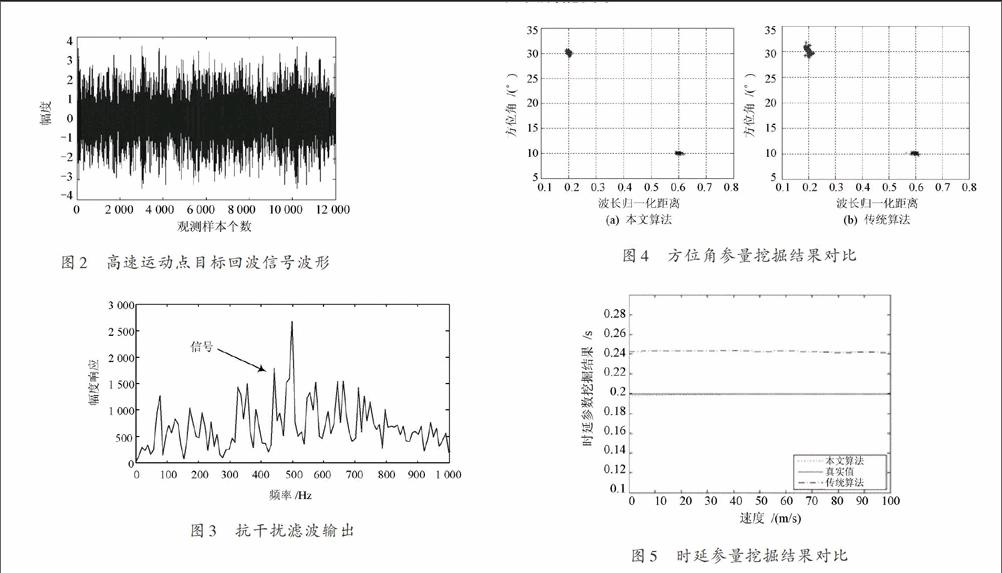
为了测试本文设计的参量挖掘算法在实现高速运动点目标运动参量估计中的性能，下面进行了仿真实验。实验的硬件环境为： Intel（R） 2.3 GHz CPU，2 GB内存，32位Windows 7系统，基于Matlab 7编程平台进行算法设计。以雷达目标信号为实例，以两个阵元的合成信号为测试对此，假设高速运动的两个点目标阵元的两个信号的频率分别为200 Hz，100 Hz，波束采样频率为4 000 Hz，得到接收的目标回波信号模型见图2。

图2 高速运动点目标回波信号波形

由图2中可见，原始的目标回波信号波形受到的干扰较重，难以实现对运动参量的有效估计，采用级联滤波算法对运动目标的干扰特征进行降噪滤波处理，得到4次级联滤波结果输出如图3所示。

图3 抗干扰滤波输出

从图3可见，采用本文算法进行信号滤波，能有效去除干扰噪声，提高了信号的纯度，进而提高参量挖掘的准确度。以此为基础，对信号提取四阶累积量时频特征，进行时频分析，实现信号的特征参量挖掘，假设高速运动点目标信源的方位角分别为10°，30°，距离分别为[0.6λ1]，[0.2λ2]，波速为1 500 m/s。实验中，假设高速运动目标的方位变换快拍数为1 000，目标回波接收基阵的阵元数为14，做50次Monte?Carlo实验，进行参量估计仿真实验。为了对比算法性能，采用本文算法和传统算法，以方位角和时延参数挖掘为例，得到结果如图4和图5所示。

从图5可见，采用本文算法，参数挖掘的估计精度较高，拟合值与真实值相同，提高了对目标参量的估计和识别能力。

图4 方位角参量挖掘结果对比

图5 时延参量挖掘结果对比

4 结 论

通过对高速运动点目标的运动参量挖掘，实现对高速运动目标的速度、时延、方位等信号源参量的准确估计，本文提出一种基于时频分析的高速运动点目标运动参量挖掘算法。首先构建高速运动点目标的信号回波模型，采用级联滤波算法对运动目标的干扰特征进行降噪滤波处理，对信号提取四阶累积量时频特征，直接获取近场源的参量，最后通过仿真实验进行了性能验证，以雷达目标信号为实例进行和性能对比测试。研究结果表明，采用本文算法能准确实现对高速运动点目标的参量估计和数据挖掘，精度较高，计算复杂度降低，提高了对高速运动目标的识别和检测能力，在目标跟踪识别和打击等领域具有较好的应用价值。

参考文献

[1] 郑纪彬，符渭波，苏涛，等.一种新的高速多目标检测及参数估计方法[J].西安电子科技大学学报：自然科学版，2013，40（2）：82?88.

[2] 靳晓艳，周希元，张琬琳.多径衰落信道中基于自适应 MCMC 的调制识别[J].北京邮电大学学报，2014，37（1）：31?34.

[3] 邓兵，陶然，平殿发，等.基于分数阶傅里叶变换补偿多普勒徙动的动目标检测算法[J].兵工学报，2009，30（10）：1034?1039.

[4] 徐骞，梁红.基于二阶统计量的近场源四维参数联合估计[J].计算机工程与应用，2011，47（23）：137?140.

[5] 张李一，张守志，施伯乐.一种不确定性数据频繁模式的垂直挖掘算法[J].小型微型计算机系统，2012，33（2）：206?209.

[6] 刘立新，张晓琳，毛伊敏.一种有效的不确定数据概率频繁项集挖掘算法[J].计算机应用研究，2012，29（3）：841?843.

[7] 石鑫，周勇，胡光波.基于信号峰脊陡变调制的雷达测距算法[J].物联网技术，2015，5（4）：12?14.

[8] 赵威.基于鱼雷自导的舰船尾流回波模型建立方法[J].舰船电子工程，2013，33（4）：81?83.