数字视频降分辨率算法的滤波器设计

袁莉+初秀娟+王志国

摘 要： 数字视频在不通终端上应用时往往需要将分辨率降低到原始分辨率的1/2或1/4。因而需要有合适的算法改善降分辨率后图像的清晰度，满足用户对显示图像质量的要求。基于视频转码的需要，针对分辨率转换算法中最常用的滤波与子采样法，设计了一种用于滤波与子采样法的5阶数字滤波器，并在编译器上进行仿真验证与评估。仿真结果显示，新滤波器表现出优异的峰值信噪比，并且在分块算法中依然优异。总之，这里提出的方法不但复杂度适中，适应性强，而且能够高效、高质量地完成数字视频降分辨率。

关键词： 视频转码； 分辨率； 滤波与子采样法； 滤波器

中图分类号： TN913?34 文献标识码： A 文章编号： 1004?373X（2015）20?0026?05

Design of filter for resolution reduction algorithm used in digital video

YUAN Li， CHU Xiujuan， WANG Zhiguo

（Suihua University， Suihua 152061， China）

Abstract： When the digital video is used in different terminals， the resolution is often reduced by a factor of 2 or 4， so a suitable algorithm is needed to improve the image sharpness after resolution reduction to meet user demands for image quality. In view of the need of video transcoding， a fifth?order digital filter used for filtering and sub?sampling method was designed， which was assessed and verified on interpreter. The simulation results show that the new filter has high PSNR （peak signal to noise ratio）， and is still excellent in the block algorithm. In short， the proposed method has moderate complexity and strong adaptability， and can achieve high efficiency and quality digital video resolution reduction.

Keywords： video transcoding； resolution； filter and sample； filter

各种数字视频实际应用在各种不同的终端设备上，如电脑、平板电脑、电视、手机等，他们支持不同分辨率和不同压缩标准的视频，因此经常存在对同一视频进行不同分辨率间转换的需求。例如使用手持终端设备接收观看运营商提供的标准清晰度数字电视节目，往往需要将节目分辨率降低到原始分辨率的[12]或[14]。因而需要有合适的算法改善降分辨率后图像的清晰度，满足人们对显示图像质量的要求。对于这样的实际需求，滤波子采样算法降分辨率的算法和物理结构实现相对简单，适合在软硬件系统中集成。但是此方法的滤波器设计尤为关键，需要大量的数学和信号系统相关的建模和演算。设计一个性能良好的滤波子采样降分变率方法，并且进行全面系统地测试，对分辨率转换相关软硬件设计有指导意义。另一方面，国内外大部分算法都是在像素域分块后在变换域（如AVS域、DCT域等）进行，保证了速度但因为分块操作引入了峰值信噪比（PSNR）的损失（称之为块效应）。对块效应的分析评估可以在转换速度与精度中找到平衡点，可以有效地指导以及优化各种算法的设计和实现，为图像领域未来的各种算法设计、程序设计和硬件设计都有深远影响。

本文基于视频转码的需要，设计并实现了一种应用于此方法的5阶数字滤波器，并在编译器上进行仿真验证与评估，取得了令人满意的结果。此滤波器在像素域8×8分块后使用，表现依然良好。

1 滤波与子采样法

滤波与子采样法降分辨率基本过程如图1所示。将图像X的行与列看做数字序列，用一个系统函数对其滤波，滤去高频分量，得到图像Y，然后等间隔取出像素点组成新的图像。

这个过程中滤波后得到的m×n像素图像（见图1中②）有[34]的像素是无用的，因为采样只取[14]的像素。所以只要确定了采样点，则只需对采样点进行滤波即可，可以省去很多计算，过程如图2所示。

注：①原始m×n像素图像；②滤波后的m×n像素图像；

③等间隔采样；④合并成新的[m2×n2]图像

图1 滤波与子采样法降分辨率（一）

注：①原始m×n像素图像；②滤波与等间隔采样同时进行；

③合并成新的[m2×n2]像素图像

图2 滤波与子采样法降分辨率（二）

综上所述，滤波与子采样降分变率方法的第1步为滤波，对于k阶的滤波与子采样降分变率方法，所用到的低通滤波器系统的方程为：

Y（n）=h0X（n）+h1X（n-1） + h2X（n-2） + … +hkX（n-k）

滤波与子采样降分变率方法的第2步子采样，及对变换后的Y等间隔采样。对于m×n到[m2×n2]的降分辨率，则要求每2行取出1行，每2列取出1列，组成新的图像。行与列可以分开考虑成一维的序列，如果滤波器系统是[Y（n）=h0X（n）+h1X（n-1）+h2X（n-2）]的低通滤波器，输入序列[X=x1，x2，…，xm]，则滤波后序列是：[Y=[h2+h1+h0x1h2+h1x1+h0x2h2x1+h1x2+h0x3+…][+h2xm-2+h1xm-1+h0xm]]。等间隔采样，结果可以是如下两种：

[Y= h2+h1+h0x1 h2x1+h1x2+h0x3 h2x3+h1x4+h0x5…；Y=h2+h1x1+h0x2 h2x2+h1x3+h0x4 h2x4+h1x5+h01x6…]

以1阶滤波子采样为例，像素域平均法是最简单形式。其实现为，每2×2矩阵的4个元素取均值，得到1个新的像素值，代替原来的4个像素。本质是对行和列同时做1阶低通滤波并采样。在一个维度上，此低通滤波器的系统函数是：[H（z）=12+12z]，低通滤波系统的差分方程是：[Y（n）=12X（n）+12X（n-1）]。长度为n的序列，滤波后得到的新序列长度仍为n，对其进行每2像素点取一点采样，得到的[12n]像素序列即为降分变率后的序列。对于二维图像，把系统函数[H（z）=12+12z]写作[H1D=1212]，则二维的系统函数为：[H=H1D×H1D=14141414]。在实际实现中，其实并不需要对每一个像素点进行滤波得到[m×n]像素图像再采样，滤波只要对采样点进行即可。所以，像素域平均法降分辨率具体实现就是每2×2矩阵的4个元素取均值，得到1个新的像素值，代替原来的4个像素。

以2阶滤波子采样为例。对连续的一行中的3个点，或对连续的3行进行变换：[Y（n）=h0X（n）+h1X（n-1）+h2X（n-2）]。此滤波器系统函数：[H（z）=h0+h11z+h21z2]或写作[H1D=h0h1]。例如，取[H1D=121412]，此系统的频率响应如图3所示，为一低通数字滤波器。二维具体实现，对每3×3个像素乘以如下矩阵得到一个新的像素点，即可同时完成对列和行的滤波，此时：

[H2D=h0h0h1h0h2h0h0h1h2h1h2h1h0h2h1h2h2h2]

如果：

[H1D=121412]

可知：

[H2D=1418141811618141814]

图3 [H1D=12 14 12]的低通滤波器

2 滤波器设计

2.1 设计滤波器阶数

简化考虑，先低通滤波再采样，先只考虑空间一维，因为二维只是2个一维变换的简单结合。首先讨论不同阶数滤波后的最佳采样结果，以1～4阶为例，这些阶数的最小偏移情形如图4所示。

图4 不同阶数无偏性最好的滤波采样方式

因此，滤波之后必须选择合理的采样方法，尽可能减小图像偏移。对于折半降分辨率，最好使用奇数阶的低通滤波器来滤波。偶数阶滤波后无论如何采样，都会引起图像中信息的偏移。

举一个简单实例，图5中①中背景是模拟图像，·表示原采样点（即数字图像像素点），×表示新采样点（降分变率后图像像素点）。方框表示降分变率数字图像一个采样点（红色×）所涵盖的图片信息。图5中②为1阶（或2抽头，或像素平均值法）滤波，采样点无偏；图5中③为2阶（或3抽头），采样点偏移；图5中④为3阶（或4抽头），采样点无偏；图5中⑤为4阶（或5抽头），采样点偏移。可以看出，对于二维情形，依然是奇数阶的低通滤波器偏移较小。考虑无偏性和算法复杂度，5阶滤波（6抽头）：Y（n）=h0X（n）+h1X（n-1）+h2X（n-2）+h3X（n-3）+h4X（n-4）+h5X（n-5），无偏移，滤波器特性较为理想。

图5 不同滤波采样法，模拟图像-数字图像-降分变率数字图像关系

2.2 设计滤波器系数

理想的数字低通滤波器幅频特性为矩形窗，如图6所示。

图6 理想的数字低通滤波器幅频特性

根据傅里叶变换，空域Sa函数，则频域为矩形窗。对Sa函数采样，则可得到矩形窗的系统函数系数。不同的采样疏密程度将得到不同的窗口宽度，如图7所示。

严格来说，可以采用FIR等方法，直接设计滤波器。采用有限冲击响应数字滤波器（FIR）设计步骤：

（1） 确定滤波器长度 N=6，群时延[α=12N-1=][2.5]；

（2） 取截止频率[ωc=π2]；

（3） 取矩形窗函数，过渡带宽度[0.9×2πN]，则由[6=N=0.9×2πω通带边-ω阻带边]得：通带<0.35π，阻带>0.65 π；

（4） [hdn=sinπ2n-απn-α]，[ωn=R6n]是矩形窗函数，群时延[α=2.5]，所以[hn=hdn×R6n=][sinπ2n-2.5πn-2.5]，n=0，1，2，…，5；

（5） 取n=0，1，2，...，5 得到[hn]，系数归一化，近似取整，得到：

[H1D=h0h1h2h3h4h5 =-0.090 0 0.150 1 0.450 2 0.450 2 0.150 1 -0.090 0 ≈-110320920920320-110 =120-23993-2]

如图8所示，这个系统函数在[ωc=π2]处衰减为-5 dB，通带起伏1 dB，阻带衰减 <-15 dB，在5阶滤波器中具有较好的低通特性。实质上，[H1D=120-23993-2]正是前面讨论到的对Sa函数的采样，如图7所示。

图7 采样疏密程度与窗口宽度的关系

图8 [H1D=120-23993-2]的幅频特性

3 算法评估与结果

3.1 测试材料

本文通过CIF格式与QCIF格式之间的分辨率转换来测试算法。CIF与QCIF格式文件（扩展名“.yuv”）每一帧图像包含3个矩阵Y，Cb，CR1。每1个像素点由8 b整数（unsigned char）记录。CIF与QCIF之间做分辨率转换时，需要对Y，Cb，Cr矩阵分别做变换。

对于降分辨率结果的测试方式，除了编译器下直接测试之外，也可以借助YUV Viewer等软件。例如，在C++下，从测试文件中读出若干帧图像，变换后写入新文件，用YUV Viewer等软件查看，可以验证正确性，并做定性分析。在做无偏性测试时，将有偏和无偏的输出图像写入连续的两帧，通过YUV Viewer等软件播放时，可以明显感受到图像偏移。

3.2 评估标准

通过某种参数来评价算法的结果是否合理。可以采用的参数很多，比如差值的绝对值的和，但是不同样本间这个参数不够明显，不宜采用。通常采用峰值信噪比来评价算法输出结果。峰值性噪比（Peak Signal Noise Ratio，PSNR）定义为[PSNR=10×log（2552MSE）]。其中：[MSE=（pixel-pixelR）2Size]；pixel，pixelR分别指被评价图像像素点和参考标准图像像素点；Size指图像尺寸，宽×高。

算法输出结果与参考标准对比，计算PSNR，用于评估算法。本文中的参考标准有两种，由DCT域法降分辨率法生成。DCT域法降分辨率是通过DCT变换（离散余弦变换），在变换域内进行的降分变率过程。DCT系数的特点是图像经DCT变换后，大部分能量都保留在DCT矩阵的低频带（左上角矩阵），去除高频系数，得到的左上角矩阵保持着图像的大部分信息。再经过逆DCT变换，可以得到低分辨率图像。

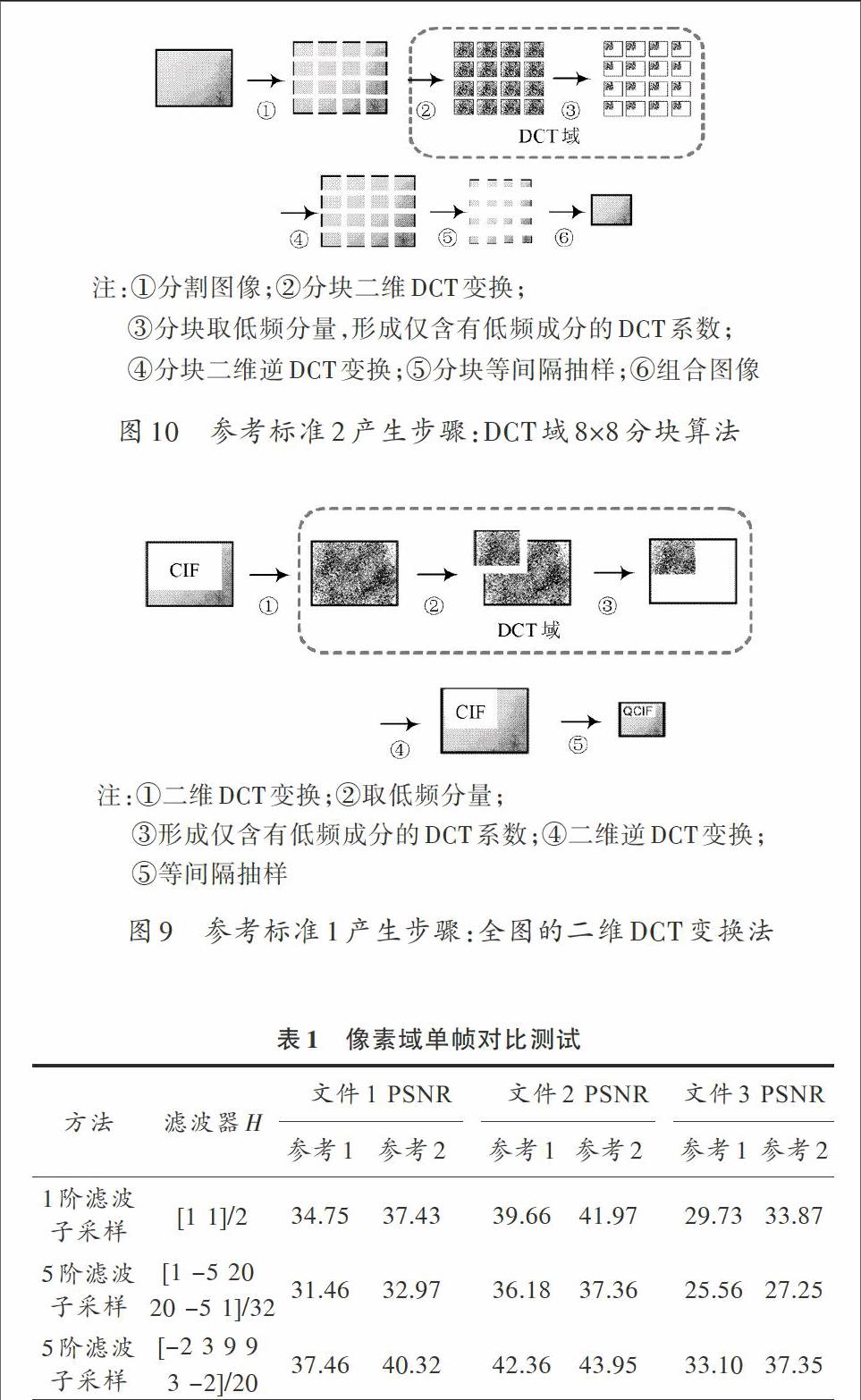
参考标准1是全图的二维DCT变换法，如图9所示。参考标准1的算法计算量很大，尤其是对整体图像做DCT变换和IDCT（Inverse DCT）变换（反DCT变换）的步骤，但是结果是较为理想的，仅用于算法对比，一般不用于实际的视频降分辨率。

注：①二维DCT变换；②取低频分量；

③形成仅含有低频成分的DCT系数；④二维逆DCT变换；

⑤等间隔抽样

图9 参考标准1产生步骤：全图的二维DCT变换法

参考标准2是DCT域8×8分块算法，如图10所示。实际的降分辨率算法中，为了降低算法复杂度，往往先对图像进行等大小分块，然后对分割得到的小图像分别进行处理。参考标准2的算法计算量适中，但是结果较参考标准1稍差，可作为实际的视频降分辨率算法。本文将其用于对像素域平均法、滤波与子采样法的评估。

这种分块的算法有时的确能大幅降低算法复杂度（尤其是DCT变换），然而它并不适用于全部算法，而且即使适用，分块也会引起的图像质量变差，这种由分块处理引起的图像质量下降称作块效应。使用时，要综合考虑计算复杂度和块效应，将图像质量的下降控制在合理、可接受的范围内。高阶的滤波子采样法不宜应用分块方法，因为会有大量的滤波抽头点在分块以外。

注：①分割图像；②分块二维DCT变换；

③分块取低频分量，形成仅含有低频成分的DCT系数；

④分块二维逆DCT变换；⑤分块等间隔抽样；⑥组合图像

图10 参考标准2产生步骤：DCT域8×8分块算法

3.3 像素域单帧对比测试

参加对比的算法：像素平均值法（1阶滤波子采样法）H=[1 1]；（5阶）滤波子采样法 H=[1 -5 20 20 -5 1]；（5阶）过滤子采样法H=[-2 3 9 9 3 -2]。测试图像：3个不同文件的第一帧，CIF格式。参考标准1为QCIF文件Ref_DCT.yuv；参考标准2为QCIF文件Ref_DCT8.yuv。

从表1可看出，宽矩形窗H=[1 -5 20 20 -5 1]得到的降分辨率图像的PSNR并不好，甚至不如1阶滤波子采样。原因是变换分辨率后保留了过多的高频分量。而本文提出的H=[-2 3 9 9 3 -220]表现出优异的PSNR。

表1 像素域单帧对比测试

3.4 块效应的影响

整块滤波采样对比 8×8分块滤波采样：4个yuv输入文件（Bridge，Foreman，Mobile，Mother?daughter），分别连续测试前300帧。测试1：以整块DCT变换为参考标准，比较PSNR；测试2：以8×8分块DCT变换为参考标准，比较PSNR。测试数据如图11所示。现在计算图11中整块与分块结果的PSNR的差值的绝对值的最大值Max[ΔPSNR]，如表2所示。可以看出，在8×8分块中，PSNR的变化并不多，在合理范围之内，说明了这个5阶滤波器在分块算法中的适应性。

3.5 综合对比测试

测试对象为CIF图像“Mobile.yuv”，一共300帧。要测试的算法包括：对整个图像的像素平均值法H=[1 1] （8×8分块后的像素平均值法与之相同）；对整个图像的滤波子采样法H=[-2 3 9 9 3 -2]；8×8分块后的滤波子采样法H=[-2 3 9 9 3 -2]。参考标准有2个：整个图像的DCT变换法；8×8分块DCT变换法。综合对比测试的结果见图12。

表2 Max[ΔPSNR]

图12 多种算法对比测试数据

分析如下：首先像素平均值法在不同参考标准下质量表现都是最差，其次结果也体现了算法分块方式相同则结果接近的特点。本文提出的5阶滤波[H1D=120-23993-2]子采样法复杂度适中，结果令人满意。此滤波方法在8×8分块中表现依然良好。

4 结 语

本文基于视频转码的需要，设计并实现了一种分辨率转换的算法，着重研究了CIF格式到QCIF格式的分辨率转换，并在编译器上进行仿真验证与评估。特别的，本文设计提出了一个性能良好的5阶滤波[H1D=120-23993-2]子采样降分变率方法，对分辨率转换相关软硬件设计有指导意义。

参考文献

[1] RICHARDSON I E. The H.264 advanced video compression standard [M]. Hoboken， New Jersey： John Wiley & Sons， 2011.

[2] RAO K R， KIM D N， HWANG J J H. 264/MPEG?4 advanced video coding in video coding standards [M]. Berlin， Germany： Springer Netherlands. 2014.

[3] GAO W， MA S. video coding basic principle in advanced video coding systems [M]. Berlin， Germany： Springer International Publishing， 2014.

[4] 王峥，郑江滨.基于 DCT 域的任意分辨率视频可伸缩编码[J].微电子学与计算机，2012（4）：45?48.

[5] 周晋.视频编码中自适应插值滤波器的算法研究[D].西安：西安电子科技大学，2011.

[6] 石巍，胡海兵，邢岩.基于多分辨率控制算法的中频有源电力滤波器[J].中国电机工程学报，2011（3）：47?51.