基于时间序列的钻压预测研究

刘光星，翟坤，陶宇龙，白晓辉

（1.西安石油大学陕西省钻机控制技术重点实验室，陕西西安710065；

2.陕西省煤层气开发利用有限公司澄合天宇勘探建井工程有限责任公司，陕西澄城715200）

基于时间序列的钻压预测研究

刘光星1，翟坤1，陶宇龙2，白晓辉1

（1.西安石油大学陕西省钻机控制技术重点实验室，陕西西安710065；

2.陕西省煤层气开发利用有限公司澄合天宇勘探建井工程有限责任公司，陕西澄城715200）

针对钻井过程中钻压的预测处理问题，为了提高钻压预测的准确度，以青海地区勘探井实钻数据为基础，提出了一种基于时间序列的钻压预测方法。运用Eviews软件建立钻压及其他重要参数的时序模型，通过时序模型对未来钻井数据进行预测处理，分别运用单因素和多因素时序建模预测方法，对实际钻压进行数值预测。最终证实，采用此方法能够实现对钻井过程中未来钻压值的预测，且具有较高的处理精度。

时间序列；建模；预测；钻压

在钻井过程中，钻井参数的变化与井下复杂情况的产生密切相关，钻压是最重要的参数之一，其在实现安全、高效的钻井施工中尤为重要，因此，有必要在实现钻压的随钻测量的前提下，对钻压的实时预测进行相关研究，进一步实现提前预测、有效控制的目的。如何根据钻进过程实际情况，对实时钻压进行预测，是钻井工作者一直奋斗的目标。时间序列分析法就是对一组随时间变化的数据或有序随机数据进行分析处理，提取其中特征信息，以及对相关数据进行预测处理的方法，且与其他方法相比，时间序列预测方法在面对海量的钻井相关数据时，可以有效地利用历史数据挖掘出有价值的信息，对未来钻井变化做出及时正确的预测，其在中短期预测处理的效果较其他方法更具优势，适应性强，拟合度更高，可以充分反映钻井相关数据的信息特点，且其具备所需数据资料较少、建模简单、计算快捷等优点。因此本文运用时间序列建模预测方法对钻井过程中的钻压值进行预测。

1　时间序列

时间序列是指按时间顺序排列的一组数据，从广义上讲是指一组有序的随机数据。单因素时间序列建模是进行多因素时间序列分析的前提和基础，其主要有三种时序模型，分别为：ARMA、AR和MA模型。ARMA模型是研究时间序列的重要方法，由自回归模型（简称AR模型）与滑动平均模型（简称MA模型）为基础“混合”构成。其基本形式如下：

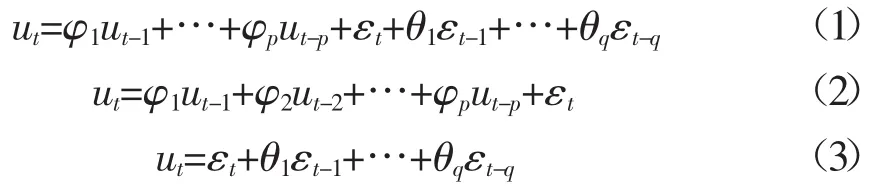
φ1，φ2，…φp是自回归系数；θ1，θ2，…θq是移动平均系数；p为自回归模型阶数；q为移动平均模型阶数；εt是均值为0，方差为σ2的白噪声序列。

ARMA模型是单因素时序方法中最基本的，实际应用最广的时序模型。它是在线性回归模型的基础上引申并发展起来的。为了能够将影响事件发展的众多因素结合起来进行综合考虑，在经过多次的反复研究和比较后，选择了在工程项目中应用广泛，也便于理解和实际计算的多元线性回归模型。

式（4）称为多因素时序模型，其中，Yt为事件在t时刻的真值；Xt，i（i=1，2，…，n）为应用单因素法对第i个影响因素在t时刻的预定值；ai（i=1，2，…，n）为各影响因素的自回归系数；at为白噪声序列。

2　单因素时序建模与预测

在运用单因素时间序列分析法建模预测钻压时，要求样本数据序列必须是平稳的，如果所给的序列是非平稳序列，则必须对所给序列做预处理，使其平稳化，然后建立ARMA模型。在此，运用Eviews软件对青海地区某勘探井的相关数据进行分析处理，首先，运用连续的90个钻压样本数据建立时序模型，通过当前ARMA模型推断下一预测值，模型是动态的；然后，剔除上一组样本的第一项，预测值作为新样本的最后项，补全样本数量，生成新的钻压时序样本，建立新的ARMA模型，继续预测下一钻压值，依此类推，逐步预测，下面直观的阐述建模预测的方法和步骤。

2.1序列的预处理及平稳性判断

图1　钻压时序图

表1　钻压的自相关系数和偏自相关系数表

由钻压时序图、自相关系数和偏自相关系数图可以明显判断出序列是平稳的，最后一列白噪声检验的Q统计量和相应的伴随概率表明序列存在相关性，序列为平稳非白噪声序列，可以对序列进行建模，偏自相关系数出现典型的截尾特性。

时序图和相关表判断序列是平稳的，需继续进行ADF序列平稳性检验（见表2），进一步证实这个结论，T统计量明显小于1%、5%和10%三个显著水平的检验值，则序列不存在明显的趋势，表明拒绝存在一个单位根的原假设，序列平稳。

2.2模型识别及参数估计

由表1可以看出，偏自相关系数在k=2后很快趋于0即2阶截尾，尝试拟合AR（1）和AR（2）模型，综合考虑ARMA模型。

在参数估计时，对原序列做描述统计分析，序列均值非0，通常对0均值平稳序列做建模分析时，需要在原序列基础上生成一个新的0均值序列，也就是用原序列的每个参数减去其均值所生成的一个新的平稳非白噪声序列，相当于在原序列基础上做了整体平移，统计特性不会发生根本改变。

表2　ADF检验结果

尝试AR模型。在方程定义时输入x ar（1）ar（2），选择最小二乘估计（LS），可以得到表3所示的建模结果，由伴随概率可知，AR（1）高度显著，不适合拟合AR（2）模型。表4为AR（1）建模结果。综合最优选取，得到钻压当前90组数据拟合的自回归模型为：

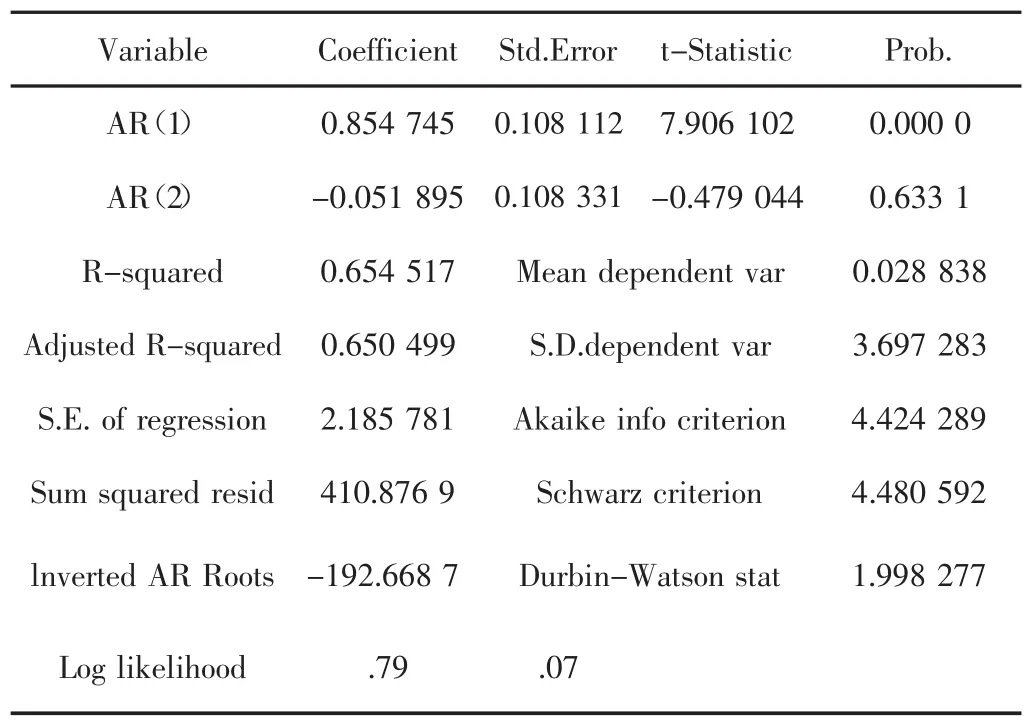
表3　AR（2）建模结果

表4　AR（1）建模结果

表3、表4中最下方给出的是滞后多项式φ（x-1）=0的倒数根，只有这些值都在单位圆内时，过程才平稳（见图2）。

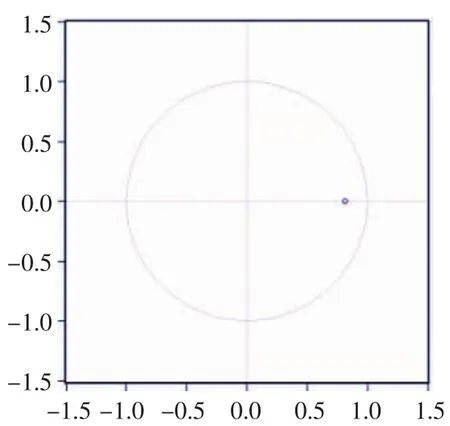
图2　根轨迹图

2.3模型检验

参数估计后，应对拟合模型的适应性进行检验，实质是对模型残差序列进行白噪声检验。若残差序列不是白噪声，说明还有一些重要信息没被提取，应重新设定模型，残差相关表（见表5）。

表5　模型残差相关表

可以看出残差序列不存在序列相关，且各阶滞后期的自相关系数和偏自相关系数值都接近于零，所有的Q统计量均不显著，因此可以判断残差为白噪声，说明拟合模型有效（见图3）。

图3　模型拟合图

综上则可以确定大钩负荷的ARMA模型拟合成功。

2.4未来钻压值预测

由于原序列是实际钻井参数值，选用静态预测，来得到第一个预测值。用同样的方法可以得到之后九次建模的钻压ARMA模型，进一步可以得到预测结果（见表6）。

表6　钻压单因素预测

通过数值比较可以得到单因素时序建模钻压预测的平均误差为：2.39%，最大相对误差为4.45%，最小相对误差为0.06%，都保持在允许误差范围内，可以满足钻进过程对钻压精度的要求（相对误差标准要求在5%以内）。

3　多因素时序建模与预测

以钻压为因变量，选取与钻压有较大相关性的四种钻井参数，如：大钩负荷、转盘扭矩、泵压和机械钻速，作为辅助变量进行多因素时序建模，选取90组正常钻进时的各钻井参数数据，建立以钻压为因变量的多因素时序模型，最优模型建立后，将各辅助变量的数值代入模型中，从而求得钻压的多因素预测值；当各辅助参数的数值为单因素时序建模的预测值时，则同样可以将各参数的预测值代入钻压多因素时序模型，从而求得钻压的多因素时序预测值，以便对实际钻井工况的钻压进行优化选取。

运用SPSS软件，建立的钻压的多因素时序模型，结果（见表7），其中t值为中间过程产生的数据，是用于计算Sig.值的，Sig.值就是显著性（significance），当Sig.值小于0.05时，则拒绝原假设；当Sig.值大于0.05时，则无法拒绝原假设。

表7　钻压多因素时序建模结果

表8　钻压多因素预测

则钻压的多因素时序模型为：

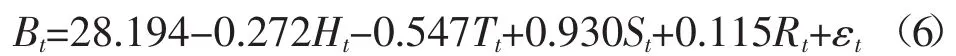
式中：Bt，Ht，Tt，St和Rt分别为钻压、大钩负荷、转盘扭矩、泵压和机械钻速的实际钻井样本序列，εt为钻压多因素时序模型中的白噪声序列。将各个辅助参数值代入钻压多因素时序模型中，从而得出钻压的多因素预测值（见表8）。

通过表8可以得到，多因素时序建模钻压预测的平均误差为3.48%，最大相对误差为7.06%，最小相对误差为0.11%，部分预测值保持在5%左右的允许误差范围内，基本满足钻进过程对钻压精度的要求，但相较与单因素预测而言，精确度较低，因此，在实钻工况中可以较大概率的选取单因素钻压预测值对钻井过程进行优化控制。

从以上研究可以看出，用时间序列预测钻压的核心问题是建立钻压预测模型，所以只要能获取不同井眼的钻井数据，都可以使用此方法建立单因素或者多因素钻压预测模型。

4　结论

时间序列建模预测方法对实际数据的依赖性较其它方法而言相对较低，扩展性强，很适合钻井工程中信息不足、不确定等情况。用此方法建立的钻压预测模型不但可以用于离线的钻压参数优选，而且也可以用于实时钻压预测；不但可以用于单井的钻压预测，而且也适合在整个矿区进行推广，此方法适用于各种不同井眼的情况（垂直井、水平井、复杂地层井等），具有较好的普遍性和适应性。

该方法在青海地区勘探井数据的建模预测中，得到的结果与实际较吻合，具有较高的精确度和可信度。因此，将时间序列建模预测方法运用到钻井钻压预测中是很有必要的，且在实际钻井中有较高的应用价值。

［1］魏武雄.时间序列分析:单变量和多变量方法（第二版）［M］.北京:中国人民大学出版社，2009.

［2］方子良，高骏，王军辉.多因素时间序列法的研究［J］.南京理工大学学报（自然科学版），2003，27（3）:298-300.

［3］唐玉娜，李启会.ARMA模型在预测问题中的应用［J］.嘉兴学院学报，2006，18（Z1）:183-187.

［4］曹彤，乔宇，等.时间序列分析中的ARMA算法及其软件实现［J］.北京联合大学学报（自然科学版），1996，10（2）:6-11.

［5］王春兴.基于Matlab实现现代功率谱估计［J］.现代电子技术，2011，34（16）:65-67.

［6］汪冬华.多元统计分析与SPSS应用［M］.华东理工大学出版社，2010.

［7］史玉生，等.基于人工神经网络的钻压优化模型的建模方法［J］.中国地质大学学报，1999，24（4）：432-436.

［8］陈廷根，管志川.钻井工程理论与技术［M］.中国石油大学出版社，2000.

［9］陈涛平，等.石油工程［M］.北京：石油工业出版社，2000.

Research on the prediction of WOB based on time series

LIU Guangxing1，ZHAI Kun1，TAO Yulong2，BAI Xiaohui1
（1.Shanxi Province Key Laboratory of Electric Drive Drilling Rig Control Technology，Xi'an Shiyou University，Xi'an Shanxi 710065，China；2.Shanxi Coalbed Methane Development Co.，Ltd.，Chenghe Tianyu Exploration Well Construction Engineering Co.，Ltd.，Chengcheng Shanxi 715200，China）

For prediction handling problems during drilling WOB，in order to improve the accuracy of prediction of WOB to Qinghai actual drilling exploration wells based on the data，we propose a method based on time series WOB prediction.Using eviews software to establish timing model WOB and other important parameters，by timing models to predict the future of the drilling data processing，respectively，using univariate and multivariate time series modeling prediction of the actual WOB numerical predictions.Finally confirmed that this method can achieve the drilling process predict future values of WOB，and has a high processing accuracy.

time series；modeling；prediction；WOB

10.3969/j.issn.1673-5285.2015.04.013

TE319

A

1673-5285（2015）04-0043-05

2014－12-29

刘光星，男（1975-），陕西汉中人，博士研究生，副教授，硕导，主要研究方向为电力拖动控制与自动化装置。