冷藏箱温度场的数值模拟及其优化

李成祥，陈建东，李娜，王德昌

（1-青岛大学能源工程研究所，山东　青岛　266071；2-江苏常发制冷股份有限公司，江苏　常州　213000）

冷藏箱温度场的数值模拟及其优化

李成祥*1，陈建东2，李娜1，王德昌1

（1-青岛大学能源工程研究所，山东青岛266071；2-江苏常发制冷股份有限公司，江苏常州213000）

本文用FLUENT软件对间冷式冷藏箱的流场与温度场进行数值模拟，分别模拟了冷藏箱开机15分钟强制对流和停机3分钟自然对流时箱体内流场与温度场的分布情况。计算结果与实验测试结果互相一致，得出模拟结果的真实可靠性。模拟结果为箱体内流场与温度场的均匀性分布提供了理论支持，为改进箱体风道结构以及送回风方式做出初步探索。

冷藏箱；温度场；流场；优化

0　引言

随着中国经济的快速发展，低温冷藏箱越来越受到人们的关注，广泛地被应用于医疗卫生领域。国内对低温冷藏箱需求量很大，但国产冷藏箱市场占有率较低，技术相对落后于发达国家，有待进一步研究发展［1］。对于冷藏箱而言，温度不仅能够影响能耗和效益，更是能够影响冷藏物品的活性；因此，长久以来，如何控制温度的稳定性、均匀性进而提高其经济效益和社会效益已成为各国学者的研究重点［2-3］。针对这一问题，国内外的研究学者在冷藏箱的制冷系统设计、箱体的优化设计、制冷剂的选择以及新的制冷技术的应用等方面做了大量的研究工作［4-6］。通过应用CFD数值模拟软件对箱体内的温度分布进行预测，为改进箱体的结构与系统的设计提供了参考意见。

本文以940 L立式间冷式冷藏箱为研究对象，建立了箱体内部空气流动的仿真模型，利用计算流体力学仿真软件CFD对其流场与温度场进行了数值模拟仿真，并将仿真结果与目前的立式间冷式冷藏箱样机的运行实验结果进行对比，证明了模拟结果的可靠性。通过对不同气流组织形式下箱内温度场和速度场的数值仿真，提出了改善箱内流场与温度均匀性的方法。

1　计算模型

1.1物理模型

为了分析间冷式冷藏箱箱体内温度场与流场的分布情况，并根据冷藏箱的实际结构，采用GAMBIT软件建立的物理模型结构如图1所示。为了仿真的方便，对现有实验测试样机的箱体内部结构做了一些简化，将箱体内部视为空腔结构［7］。箱体的尺寸为563 mm×1，025 mm×1，523 mm，强制风冷系统，箱体内温度恒定控制在275.15～281.15 K；前为透明中空玻璃，其他面为钢板和隔热材料，前门框两侧竖直安装照明灯。3个回风口布置在蒸发器的前部，并且有3个轴流式风扇；风道布置在箱体后部，送风口以一定角度向下送风。

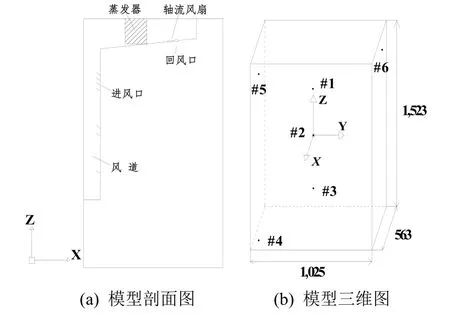
图1　改进前物理模型

1.2数学模型

冷藏箱坐标系如图1所示，用FLUENT仿真模拟可以抽象为侧面加热的矩形空腔。当雷诺数很小时，流动相对稳定，而当雷诺数较大时，便会产生Hopf分歧。对于箱体而言，雷诺数较小，流动的解是唯一且稳定的［8-9］。

采用风机和压机同步运行的方式，根据实验测试数据，同步运行15分钟，停止3分钟。因此，在仿真模拟中该冷藏箱系统内部的空气流动存在两种换热情况：风机运行时为强制对流换热，风机停机后为自然对流换热。把整个箱体作为研究对象，包括蒸发器、风扇、箱体以及内部的空气，把箱体的外壁面作为边界；计算过程中，将箱体内部的对流换热和保温层的热传导统一求解［10］。环境温度已知，环境与箱体外壁之间的传热属于第三类边界条件［11］。

为了得到箱体内流场与温度场的分布情况，本文建立了流体流动和传热数学模型。在计算区域内，流体的流动和传热特性应该满足质量、动量与能量守恒方程。在建立数学模型时做出如下假设［12-13］。

1）开机后，蒸发器的温度设为恒定；停机后，考虑蒸发器的蓄冷对箱体内流场与温度场的影响（为求解方便，蒸发器温度亦为恒值，此值为实验所测停机后蒸发器温度的平均值）。

2）因箱体内的温度要求为275.15 K～281.15 K，故忽略箱体内的相变过程，即箱体内的空气为干空气且为不可压缩的牛顿流体，且cp为定值。

3）强制对流时，箱体内空气流动为湍流；自然对流时，流体流动为稳定层流。

4）箱体内空气在内壁面上流动属于无滑移边界条件。

5）满足Boussinesq假设，即：忽略不计流体中的粘性耗散。

根据上述假设，计算中考虑了壁面辐射的影响，设定模型为标准的湍流模型。数值仿真所采用的控制方程如下。

1）连续性方程

2）动量方程

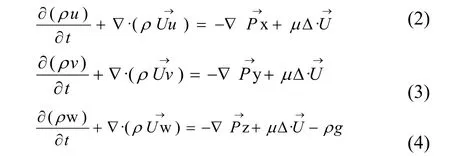
3）能量方程

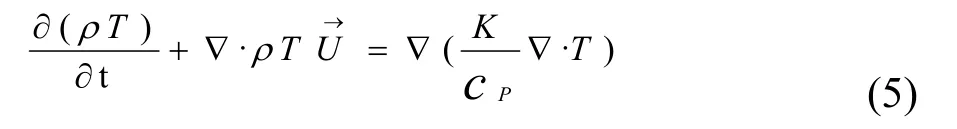
其中：

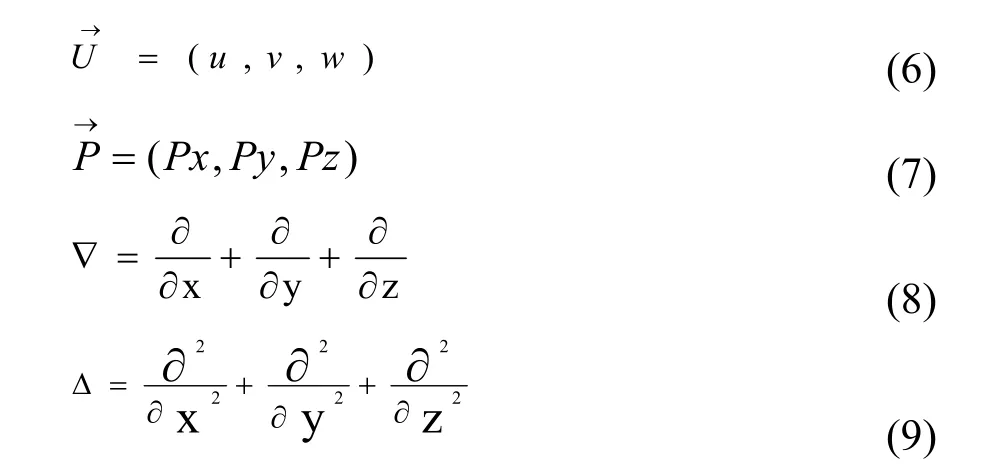
式中：

u、v、w——x、y、z方向的速度，m/s；

P——压强，Pa；

ρ——密度，kg/m3；

cp——定压比热容，kJ/（kg·K）；

K——传热系数W/（m2·K）；

μ——空气动力粘度，Pa·s；

t——时间，s；

T——温度，K。

2　网格划分及边界条件

冷藏箱箱体内部区域和风道区域采用Tet/Hybrid网格形式进行非结构化网格划分，由于不同部件网格划分完成之后可能无法实现网格节点的一一对应，因此部件间的网格交界面用interior，使之能够更好地交接。

冷藏箱开机时，风机启动，此时风道和箱体是联通的，换热方式为强制对流，箱体模型中简化风机模型，将风机区域做边界条件处理，风机出口位置设置为压力入口30 Pa，进风口位置设置为压力出口0 Pa，残差精度为10-6；冷藏箱停机时，风机停止工作，箱体内换热方式为自然对流，风道与箱体内部空气循环量少，可忽略不计，因此仿真时可去除风道区域仅模拟箱体内部空气流动情况。假设强制对流和自然对流时的环境温度相同，但箱体内部温度不同，两者的壁面综合换热系数亦不同，需分别考虑。箱体内流体流速比较低，因此不考虑气体的粘性［14］。

表1　边界条件

箱体隔热材料采用硬质聚氨酯泡沫塑料，导热系数为（0.016～0.023）W/（m·K），发泡后外壳与内胆可以铸成严密的整体，使箱体有较高的密封性和强度以及硬度；由于箱体的外壁温度基本接近于外界环境温度（实测表明两者相差不大），而且环境温度易于测得，故箱体的外壁温度取为环境温度；箱体壁面的传热是多层平壁（包括外壳、绝热层和内胆）的传热过程。

采用PRESTO方式离散速度—压力，采用二阶迎风格式，最终模型用SIMPLE算法求解。

3　计算结果分析

3.1仿真模型的验证

为了验证所建数学模型的有效性，将图1所示的冷藏箱内仿真结果中各点的数据与实验测试结果数据进行对比分析，如表2所示，其中#1、#2、#3分别为箱体上层中心、中心、底层中心，#4为箱体下左外，#5为上左外，#6为上右里，具体如图1中所注。

从表2中我们可以看到，仿真结果与实验结果符合较好，最大偏差不超过1.33%，验证了所建数学模型的可靠性，数值模拟的结果能够反映内部流场与温度场的分布规律，可以用于分析研究冷藏箱内部温度场和流场的优化。在此基础上，为了提高箱内温度场的均匀性，针对该冷藏箱内流场与温度场的分布情况，对原有结构进行改进，改进后两种方案的物理模型如图2所示。

方案一将冷藏箱的制冷系统布置在箱体下部，同样忽略掉除蒸发器以外的部件，3个轴流式风扇布置在U型蒸发器的后部，风道布置在箱体后部，送风口布置在箱体上部，垂直向下送风。方案二对冷藏箱原制冷系统的位置不做改动，将原出风口由矩形改为圆形，并向下布置，具体如图2所示。

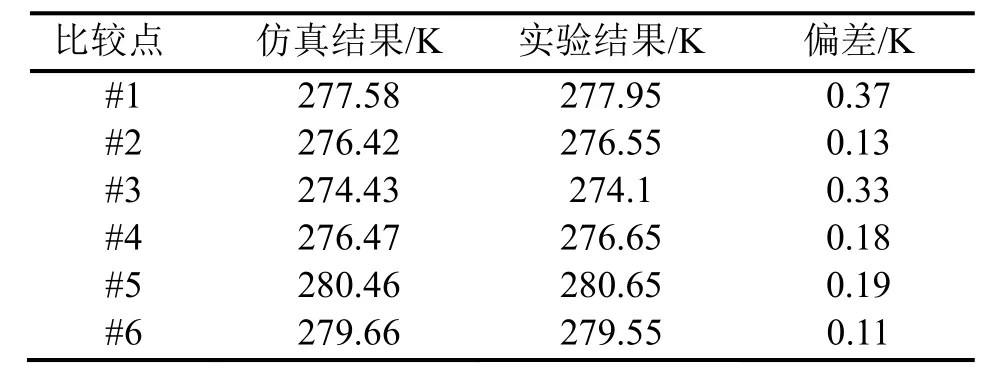
表2　仿真结果与实验结果对比分析

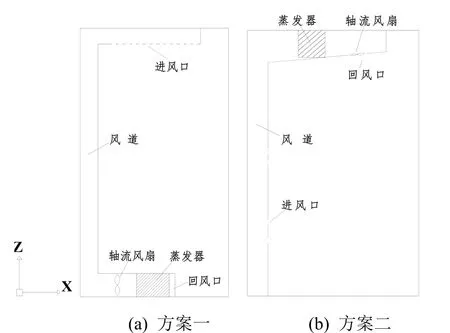
图2　改进后箱体内部结构

3.2 结构优化前后对比

图3分别给出了原有结构下冷藏箱开机与停机后箱体内部的流场与温度场的分布情况，此时蒸发器布置在冷藏箱上部，采用上送上回的送风方式；外界环境热空气通过与外壁的热对流、保温层内的热传导和内胆壁与内部空气的对流换热的传热过程将热量传入箱体内部。从温度分布图上可以看出，贴近后壁送风口的区域温度较低，从后壁往前温度呈多层分布，从送风口位置往两侧壁呈递增趋势；由于回风口在冷藏箱的上部，因此温度最高处出现在左上部和右上部，与实验结果基本吻合。

从温度场分布图上可以看出，由于冷藏箱蒸发器和风道的蓄冷以及内部各部分之间的温差引起了空气的自然对流，热空气由于浮力从下部向上，冷空气从上往下运动，造成上部温度上升较快，下部温度上升较慢。从温度等值线分布图可以看出，冷藏箱上部远远超出所要求的温度上限。

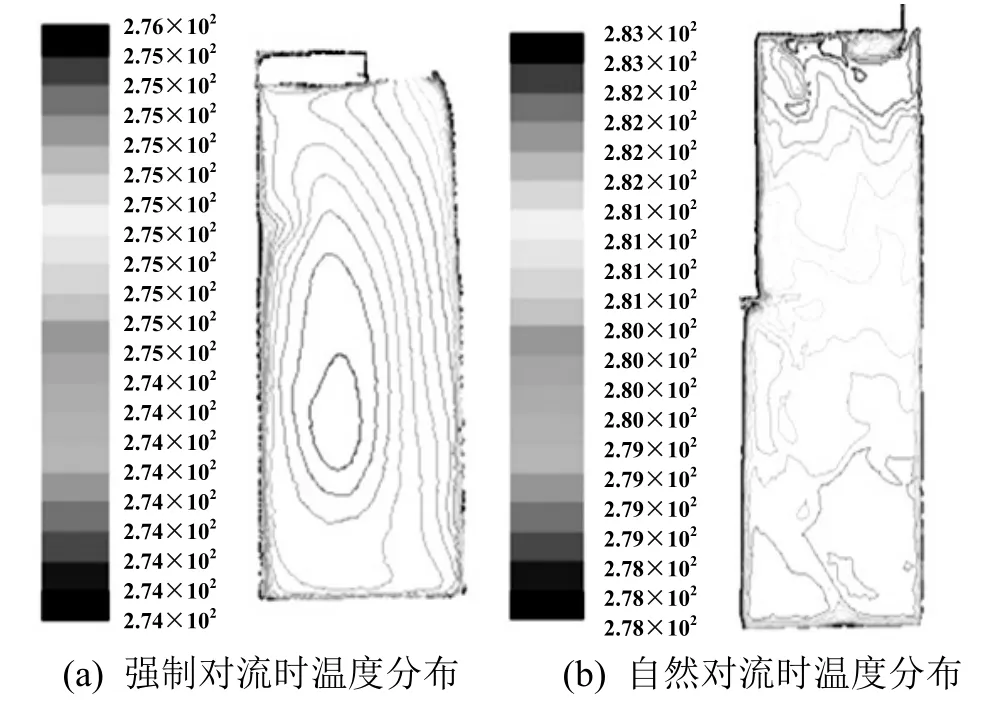
图3　原结构下强制对流和自然对流时箱体内温度场分布（Y=0，图中单位为K）

针对上述出现的问题，对原有结构进行改进，图4为改进后方案一的仿真结果，分别给出了蒸发器在下部，采用上送下回的送风方式时，强制对流换热与自然对流换热时冷藏箱箱内（Y=0平面）流场与温度场的分布情况；从温度场分布图中可以看出，此时从下部往上温度呈下降趋势，从后壁往前呈上升趋势，温度呈层状分布，左上和右上部没有出现高温区，且冷藏箱内整体温差较蒸发器布置在上部采用上送上回的方式减小许多，温度场和流场分布更为均匀。由于冷藏箱内部温差的存在，热空气因浮力从下部向上，经过与周围环境的热交换后，上部温升较快，下部温升较慢，箱内温度呈层状分布，内部最高温度低于所要求的最大温度，满足了保存物品的需要。

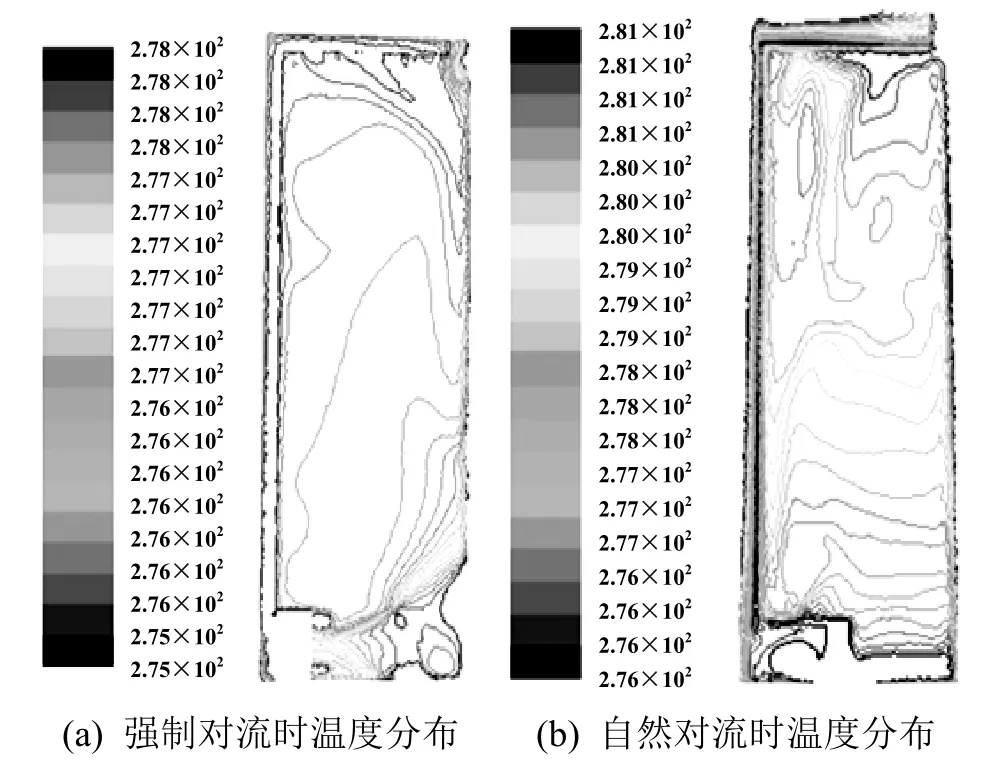
图4　方案一强制对流和自然对流时箱体内温度场分布（Y=0，图中单位为K）

图5为改进后方案二的仿真结果，分别给出了强制对流换热与自然对流换热时箱体内（Y=0平面）流场与温度场的分布情况，方案二对原有结构做很小的改动，仅对风道中出风口的形状做了改动，将矩形风口改为圆形风口，并取消了原矩形风口中的挡流板。从温度场分布图中可以看出，强制对流时箱体内从下往上，从后往前，温度分布为层状分布，与原有结构相似，上部出现高温区，但是最高温度与平均温度有所下降，最高温度低于所要求温度范围的上限；自然对流时温度上升较小，分布较为均匀，箱体内部的最低温度与最高温度均比原有结构时要低，改进效果较为明显。

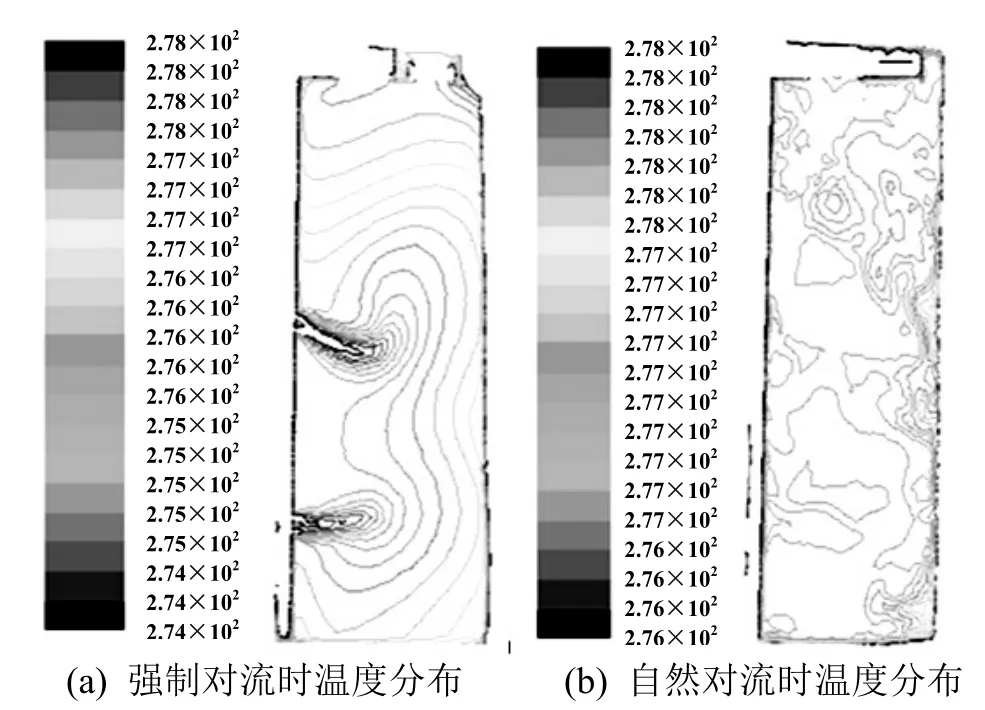
图5　方案二强制对流和自然对流时箱体内温度场分布（Y=0，图中单位为K）

尽管此方案与方案一相比，对原有结构改动较小，但是也有许多不足之处，从温度图上可以看出，由于取消了风道中挡流板，强制对流时风口附近会出现低温区，对保存的物品不利。表3中列出了原有结构、方案一与方案二下强制对流与自然对流箱体内的最低温度、最高温度以及平均温度。

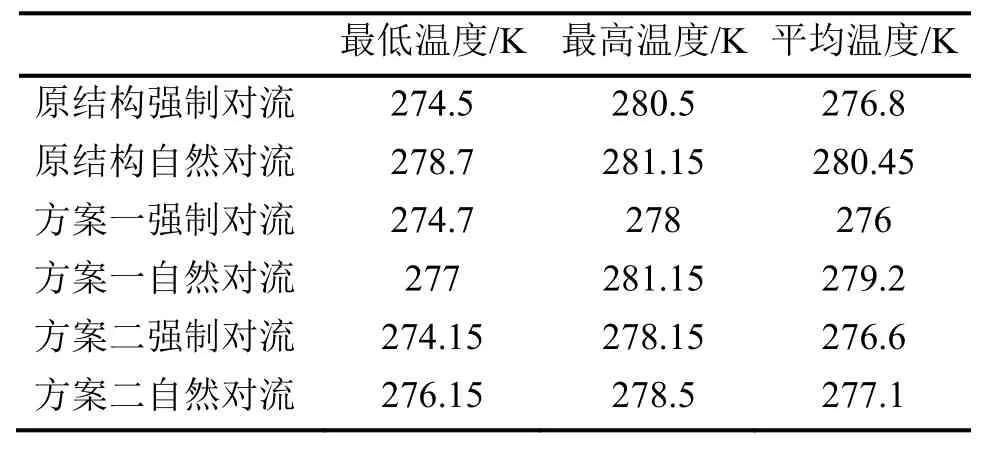
表3　最低温度、最高温度以及平均温度对比

4　结论

本文改变蒸发器的位置和形状以及出风口的位置和尺寸，对不同结构形式下的冷藏箱建立了三维计算模型，并用FLUENT分别进行了仿真；原来的冷藏箱蒸发器在顶部布置，风机布置在蒸发器的前部，送风口在后壁中上部，采用上送上回的送风方式，以致于在停机时会出现上部温度过高，下部温度过低，甚至超出允许范围的情况。

针对上述问题，文章提出了另外两种风道布置方式，将蒸发器布置在底部，送风口布置在顶部，形成上送下回的送风方式，以及在原有结构下将风道出风口由矩形改为圆形，并将风口位置下移。结果表明，方案二中将出风口由矩形改为圆形，并将位置下移，箱体内的最低温度、最高温度与平均温度都有所下降，箱体内温度场的分布均匀性有所提高，尤其是自然对流时；但这种结构也有缺点，就是在风口位置容易出现低温区。方案一中冷藏箱采用这种蒸发器和风道布置结构时，箱体内部流场与温度场的分布比较均匀，温差在所要求的范围之内，并无温度偏高或者偏低的现象，尤其在停机时箱内温度也能够满足所允许的温度上限范围；这种结构不仅有利于物品的保存，又能降低冷藏箱的能耗，是一种合理的结构形式。

［1］张金秋.-86℃医用低温冷柜性能的实验研究［J］.节能，2012（9）∶34-39.

［2］SMALE N J，MOUREH J，CORTELLA G.A review of numerical models of airflow in refrigerated food applications［J］.International Journal of Refrigeration，2006（29）∶911-930.

［3］BORGES B N，HERMES C J L，GONÇALVES J M，et al.Transient simulation of household refrigerators∶A semi-empirical quasi-steady approach［J］.Applied Energy，2011（88）∶748-754.

［4］余克志，陈天及，谢堃，等.采用系统仿真方法数值模拟双层风幕立式陈列柜［J］.制冷技术，2012，32（3）∶72-75.

［5］刘英志，刘业凤.商用冷冻柜热气融霜系统优化的实验研究［J］.制冷技术，2014，34（4）∶27-30.

［6］李恒国，户建波.冷柜门体与箱体配合间隙对能耗的影响［J］.制冷技术，2013，33（4）∶60-62.

［7］LAGUERRE O，AMARA S B，MOUREH J，et al.Numerical simulation of air flow and heat transfer in domestic refrigerators［J］.Journal of Food Engineering，2007，81（1）∶144-156.

［8］吴小华，张璟，宋春节.冰箱冷藏室温度场和流场的仿真与优化［J］.北京石油化工学院学报，2006，1（3）∶8-12.

［9］FUKUYO K，TANAAMI T，ASHIDA H.Thermal uniformity and rapid cooling inside refrigerators［J］.International Journal of Refrigeration，2003，26（2）∶249-255.

［10］费祥麟.高等流体力学［M］.西安∶西安交通大学出版社，1993.

［11］NEGRAO C O R，HERMES C J L.Energy and cost savings in household refrigerating appliances∶A simulation-based design approach［J］.Applied Energy，2011，88（9）∶3051-3060.

［12］ANTÓNIO C C，AFONSO C F.Air temperature fields inside refrigeration cabins∶A comparison of results from CFD and ANN modelling［J］.Applied Thermal Engineering，2011，31（6）∶1244-1251.

［13］毛正荣，赵巍，张华，等.低温冷柜内空气的传热与流动特性研究［J］.上海理工大学学报，2003（1）∶21-23.

［14］傅烈虎，丛伟，李青冬.冰箱内温度场与流场数值模拟［J］.制冷，2008，27（1）∶75-80.

Numerical Simulation and Optimization of Temperature Field inside a Freezer

LI Cheng-xiang*1，CHEN Jian-dong2，LI Na1，WANG De-chang1
（1-Energy Engineering Research Institution，Qingdao University，Qingdao，Shandong 266071，China；2-Jiangsu ChangFa Refrigration CO.，LTD.，Changzhou，Jiangsu 213000，China）

The computational fluid dynamics（CFD）software FLUENT was used to simulate the temperature field and flow field inside an indirect cooling freezer.It simulated the distribution of temperature field and flow field inside the cabinet with force convection in 15 minutes and the natural convection in 3 minutes.The computing results matched well with the experimental results，and the dependability of the simulation results was obtained.It provides theoretical support for uniform distribution of temperature field and flow field inside the cabinet，making a preliminary exploration to improve the box structure and air supply.

Freezer；Temperature field；Air flow field；Optimization

10.3969/j.issn.2095-4468.2015.03.109

*李成祥（1987-）男，在读研究生。研究方向：冷藏箱流场与温度场的数值模拟。联系地址：山东省青岛市市南区宁夏路308号青岛大学，邮编：266071。联系电话：15865548852。E-mail：wdechang@163.com。