基于Lattice-Boltzmann方法的泡沫材料有效导热系数研究

康利云，阚安康，曹丹，王冲，郝方园

（上海海事大学商船学院，上海　201306）

基于Lattice-Boltzmann方法的泡沫材料有效导热系数研究

康利云*，阚安康，曹丹，王冲，郝方园

（上海海事大学商船学院，上海201306）

为了提高泡沫多孔材料有效导热系数的数值计算精度，文章提出一种用计算机软件处理泡沫多孔材料电镜图，计算泡沫多孔材料的体积分数，并建立了用Lattice-Boltzmann方法（LBM）计算的物理模型。在此基础上，用D2Q9LBM模型计算泡沫多孔材料有效导热系数。通过模拟结果与实验结果对比，研究泡沫多孔材料的有效导热系数。研究结果表明模拟具有很高的精度；当体积分数从0.04增加到0.09时，有效导热系数随固相体积分数的增加而近似线性增加；当体积分数小于0.04且继续减小时，有效导热系数下降较快。

格子；泡沫；导热系数；体积分数

0　引言

泡沫多孔材料具有独特的结构和特性，所以在很多工程领域得到了广泛的应用［1-5］。对泡沫多孔材料的研究具有很长的历史，其中对孔隙率及有效导热系数的研究是对泡沫多孔材料特性研究的重要组成部分。孔隙率及有效导热系数都可用实验来测定，但测定过程复杂，且当泡沫材料内部填充流体或孔隙率较大时候，实验更加困难。因此有必要建立一种通用性强且精度高的数值计算模型。传统的对于多孔介质研究一般都采用连续介质模型，但连续介质模型只能反映多孔介质“整体”的特性，而不能揭示其内部微观构造特性。上世纪八十年代末，国际上许多学者提出将宏观流体力学与微观分子动力学连接起来的介观理论，通过发展基于分子运动论（气体动理学理论）Boltzmann方程的介观数值模型来再现特征尺度达微、纳米量级的气体流动问题［6-7］。LBM随之产生，LBM是一种介观的研究方法，与传统的计算流体力学方法（如有限单元法、有限差分法等）相比，Lattice-Boltzmann方法具有边界条件容易设定、并行性高、能直接模拟有复杂几何边界的诸如多孔介质等连通域流场而无须作计算网格的转换，正是这些优点使LBM在处理多孔介质内部传热传质领域具有天生的优势［8-10］。

利用泡沫材料的电镜图进行LBM计算不仅生成物理模型简单，而且能够真实地描述泡沫多孔介质内部的微观结构。文章详细介绍了如何利用计算机软件来处理泡沫多孔介质电镜图，计算样品固相体积分数，并最终建立LBM计算的物理模型。文章以聚氨酯泡沫为例，在实验的基础上检测聚氨酯泡沫样品的固相体积分数，并研究其固相体积分数与有效导热系数之间的变化关系。

1　LBM导热模型

本文采用D2Q9的LBM模型，温度演化方程为：

式中：

fa——温度分布函数；

r——位置矢量；

t——实时时间；

δt——时间步长；

τ——无因次弛豫时间；

feq——fa的局部平衡态分布函数；

eα——离散速度。

离散速度eα选取为：

局部平衡态分布函数eqfα为：

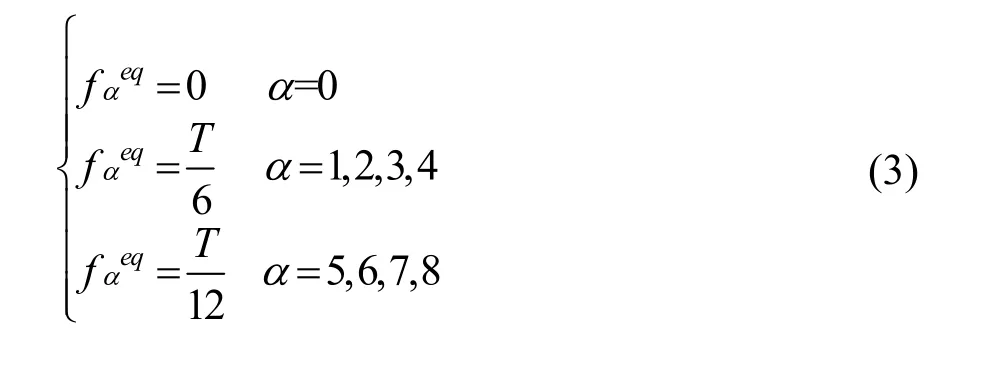
无因次弛豫时间τ为：

为了保证计算结果的准确性，τ取开区间（0.5，2）内的任何值，而τ值的大小通过c = δx/δt来调节。为了确保相面间温度和热流的连续性，令体积热容满足下列关系：

节点温度和热流密度可由以下公式求：

式中ki，j为节点（i，j）节点所处相的导热系数。当每一节点的热流密度求出之后，由傅里叶定律可以求得等效导热系数：

式中：

L——传热方向上两恒温截面之间的距离；

q——传热方向上穿越横截面的稳态热流密度；

∇T ——传热方向上两端面的传热温差。

2　建立物理模型及确定结构参数

2.1物理模型的建立

利用电子显微镜扫描拍摄聚氨酯泡沫的微观结构得到样品的电镜扫描图，通过计算机软件对电镜图进行预处理，主要包括：对图像的剪切、滤波（去除电镜拍摄时外部因素造成的噪声点）、直方图均化（增加对比度，便于二值化处理）及二值化［11-12］。由二值化矩阵计算其固相体积分数，并将图片二值化得到的矩阵导入到计算程序中。具体步骤如图1所示。

聚氨酯泡沫材料电镜扫描图及二值化后的图像分别如图2和图3所示。

图1　电镜图处理流程图

图2　聚氨酯泡沫电镜图

图3　聚氨酯泡沫二值图像

由于多孔介质本身的一些性质导致取镜部位的结构略有差异，基于多孔材料微观结构的随机性及统计原理，我们要对同一样品的不同部位取镜，对于质地不是很均匀的材料还可以将样品抛开，取其内侧断面的电镜图，这样可以有效地提高计算的精度。

2.2结构参数的确定

2.2.1固相体积分数的确定

如图1所示，电镜图进行滤波、直方图均化以及二值化处理后，将二值化结果保存为二值矩阵（0代表孔隙所在区域，1代表固相区域），利用计算机软件编程统计二值矩阵中0元素和1元素的数目，从而得到孔隙率或固相体积分数。

2.2.2孔隙特征尺寸的确定

在泡沫材料的加工过程中，由于设置工艺参数的不同，导致泡沫材料的孔隙尺寸不等。取每种样品多张不同的电镜图，用Photoshop的标尺量取每张电镜图各个孔隙的最小直径及最大直径，然后取平均值作为该孔隙的当量直径，根据当量直径范围内的孔隙数绘制出柱状图。泡沫材料的孔隙特征尺寸取各当量直径范围中值的加权平均值。由直径分布图4可知，聚氨酯泡沫材料孔隙当量直径径主要分布在140 μm～240 μm的范围内，基本呈正态分布。

3　结果与讨论

如图5所示，计算区域取正方形，划分为200×200的网格，上下边界为恒温边界，上边界温度为Ts，下边界温度为Tx（Ts＞Tx）；为了计算方便，设左右边界为绝热边界。对于上下等温边界采用非平衡态外推格式；对于左右绝热边界采用镜面反射格式处理，从而可以避免能量的泄露。由于实验过程是在环境温度为286 K下进行，所以我们设Ts=296 K、Tx=276 K，这样可以减小模拟结果与实验值之间的误差。环境温度为286 K时，空气导热系数为0.0056 W/（m·K），聚氨酯泡沫材料密度为0.0368 g/cm3，聚氨酯固相导热系数取0.262 W/（m·K）。

基于统计原理及随机因素影响，计算结果为多次计算取平均值。通过用模拟结果与实验值之间做对比，验证模拟结果的正确性，并分析有效导热系数与固相体积分数的变化关系。

图4　孔隙的直径分布图

图5　物理模型示意图

表1为聚氨酯泡沫材料固相体积分数的计算结果与实验值的对比，固相体积分数是影响多孔介质有效导热系数的关键因素，从表1可知计算结果与实验的测量结果误差保持在3%之内，这进一步保证了后续有效导热系数的计算精度。

表2为聚氨酯泡沫材料有效导热系数的模拟结果与实验值之间对比，通过表中数据对比可知，模拟结果与实验值之间误差较小，保持在2%范围内，足以保证科研及工程应用要求。

表1　聚氨酯泡沫固相体积分数模型计算结果与实验结果对比

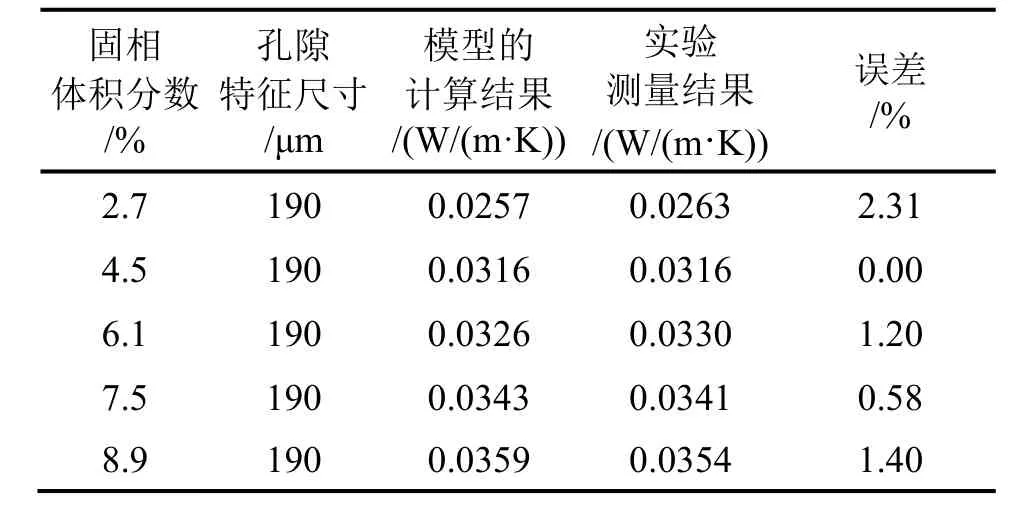
表2　聚氨酯泡沫材料有效导热系数模拟结果与实验结果对比

图6为孔隙特征尺寸为190 μm时，有效导热系数随固相体积分数在0.02～0.09范围内的变化关系图。从图6可知，利用电镜图计算的聚氨酯泡沫材料有效导热系数值与实验值不仅变化趋势相同，而且二者之间误差很小，且当泡沫体积分数在0.04～0.09范围变化时，泡沫材料的有效导热系数随泡沫固相体积分数的增加而近似线性增加；当泡沫固相体积分数小于0.04且继续减小时，材料有效导热系数会减小得更加明显，这与实验测量结果相吻合，进一步证明模拟结果的正确性。由于固相体积分数是影响多孔材料有效导热系数的关键因素，因此所建物理模型与样品的体积分数是否相同直接影响到模拟结果的精度甚至正确性。由表1可以看出，用所建物理模型计算得到的聚氨酯泡沫材料固相体积分数与实验测量的结果误差很小，精度可以保持在小数点后两位，完全满足科研及工程需要。

图6　聚氨酯泡沫有效导热系数随固相体积分数变化图

4　总结

1）通过聚氨酯泡沫材料电镜图建立的LBM计算模型能够准确地计算出样品的真实固相体积分数，这将进一步保证后续模拟结果的精度。

2）由实验对比可知，基于电镜图建立的泡沫多孔介质物理模型，利用D2Q9LBM模型，能够准确地测量泡沫材料的有效导热系数。这是由于电镜扫描图自身就是泡沫材料内部微观结构的真实表述，本身就是将泡沫材料样品真实微观结构转化为二值矩阵进行数值计算，这就能够真实客观地反映材料本身的微观构造特性。

3）影响泡沫材料有效导热系数的主要因素是泡沫固相体积分数。泡沫材料的有效导热系数随泡沫体积分数的增大而增大，且当泡沫体积分数在0.04～0.09范围变化时，泡沫材料的有效导热系数随泡沫固相体积分数的增加而近似线性变化。当泡沫体积分数小于0.04且继续减小时，材料有效导热系数下降较快。

［1］许旭东，胡海涛，杨怀毅，等.析湿工况下泡沫金属内湿空气传热传质特性的实验研究［J］.制冷技术，2014，34（6）∶5-8.

［2］马立，刘芃，胡培.PMI泡沫材料在航天器结构中应用的可行性研究［J］.航天器环境工程，2010，27（2）∶164-168.

［3］江德龙，武卫东，陈小娇.金属基体超疏水表面抗凝露抗结霜特性的研究进展［J］.制冷技术，2015，35（1）∶41-47.

［4］高恩元，荆华乾.番茄冷链运输保鲜技术研究［J］.制冷技术，2014，34（5）∶49-53.

［5］曹明法，胡培.船用玻璃钢/复合材料夹层结构中的泡沫芯材［J］.江苏船舶，2004，21（2）∶3-6.

［6］MENAMARA G R，ZANETTI G.Use of the Boltzmann equation to simulate lattice automata［J］.Physical Review Letters，1988，61∶2332-2335.

［7］HIGUERA F J，JIMENEZ J.Boltzmann approach to lattice gas simulation［J］.Euorphys Lett，1989，9（7）∶663-668.

［8］WANG M，HE J H ，YU J Y ，et al.Lattice Boltzmann modeling of the effective thermal conductivity for fibrous materials［J］.International Journal of Thermal Sciences，2007，46（9）∶848-855.

［9］PAEK J W，KANG B H，KIM S Y，et al.Effective thermal conductivity and permeability of aluminum foam materials［J］.Thermophys，2000，21（2）∶453-464.

［10］CHEN X，HAN P.A note on the solution of conjugate heat transfer problems using SIMPLE-like algorithms［J］.International Journal of Heat and Fluid Flow，2000，21（4）∶463-467.

［11］阮秋椅.数字图像处理学［M］.北京∶电子工业出版社.2001.

［12］章毓晋.图像处理［M］.北京∶清华大学出版社.2006.

Research on Effective Thermal Conductivity of Foam Material Based on Lattice-Boltzmann Method

To improve the calculation accuracy of effective thermal conductivity of the foam material，a method using computer softwares to process electron micrographs of the foam material was presented to calculate the volume fraction of foam materials，and the physical model using Lattice-Boltzmann Method（LBM）was built.Basing on it，the D2Q9LBM model was used to calculate the effective thermal conductivity of the foam material.Comparing simulation results with experimental results，the effective thermal conductivity of the foam material was studied.The results show that the simulation has high accuracy.When the volume fraction increases from 0.04 to 0.09，the effective thermal conductivity increases approximately linearly；when the volume fraction is reduced to less than 0.04 and decreases continuously，the effective thermal conductivity decreases rapidly.

Lattice；Foam；Thermal conductivity；Volume fraction

10.3969/j.issn.2095-4468.2015.03.104

*康利云（1990-），男，助理工程师，硕士。研究方向：多孔介质传质传热。联系地址：上海市浦东新区临港新城海港大道1550号，邮编：201306。手机：13817814803。E-mail：kangliyun11@163.com。

国家自然基金（No.51476094），上海市自然基金（No.15ZR1419900），上海海事大学研究生创新基金资助项目（No.YXR2014010）