一类四阶脉冲微分方程边值问题解的存在性

庄乐森，李姗姗

（新乡学院数学与信息科学学院，河南新乡453003）

一类四阶脉冲微分方程边值问题解的存在性

庄乐森，李姗姗

（新乡学院数学与信息科学学院，河南新乡453003）

研究了带脉冲的四阶微分方程边值问题，用不动点指数定理证明了此问题在适当条件下存在两个非负解。

脉冲边值问题；不动点指数定理；非负解

四阶微分方程边值问题在现实生活中有着广泛的应用，因而受到了人们的重视，许多学者对此进行了深入的研究，并取得了一些有用的成果［1-4］，但到目前为止，带脉冲的四阶微分方程边值问题的研究还比较少。作为微分方程的一个重要分支，带脉冲的四阶微分方程边值问题能描述突变现象对事物发展的影响，已在生物学、医学和航天等研究领域得到了广泛的应用。在本文中，我们研究了带脉冲的四阶微分方程边值问题

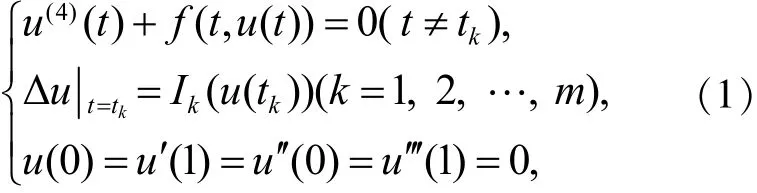
1　预备知识及引理

的解。其中：当0≤t≤s≤1时，G（t，s）=t；当0≤s≤t≤1时，G（t，s）=s。

根据函数G（t，s）的形式，可以得出G（t，s）具有下列性质：对于任意的t、s∈J，G（t，s）≥0，并且是连续的；对于任意的t、s∈J，有G（t，s）≤G（s，s）≤1；对于任意的t∈［a，b］和s∈J，有G（t，s）≥σG（s，s）；对于任意的t、s∈［a，b］，有G（t，s）≥a。在以上式子中，a∈J1，b∈Jm，σ=min｛a，1-b｝。

定义积分算子T为

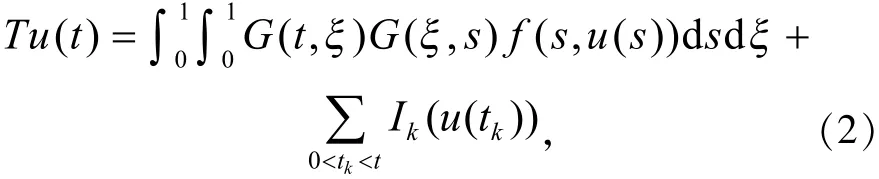
则有如下引理。

引理3：算子T是PC［J，ℝ］到PC［J，ℝ］的全连续算子。

证明：对于任意的u∈PC［J，ℝ］，由（2）式可知，Tu∈PC［J，ℝ］，因为G（t，s）、f （t，u（t））以及Ik均为连续函数，所以T在PC［J，ℝ］上是连续的。对PC［J，ℝ］中任意有界集S，T（S）中的函数均在J上一致有界，并且在每个Jk（k=1，2，…，m）上等度连续，于是由Ascoli-Arzela定理可知，T（S）是PC［J，ℝ］中的相对紧集，因此T是全连续算子。

引理4：u（t）∈PC［J，ℝ］∩C4［J′，ℝ］为（1）式解的充要条件是u（t）∈PC［J，ℝ］为算子T的不动点。

证明：由引理2可知结论成立。

引理5［5］：设X是实Banach空间E的一个收缩核，X1是X的一个有界凸收缩核，U是X的非空开集，且U∈X1。又设A： X1→X是全连续算子，A（X1）⊂X1，并且A在X1U上没有不动点，则必有i（A，U，X）=1。

2　主要结果

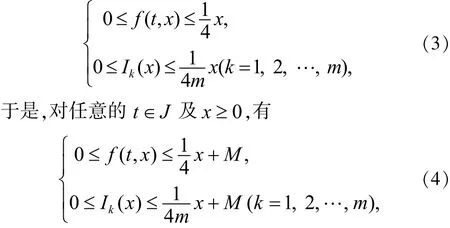
3　定理的应用

考察带脉冲四阶微分方程边值问题

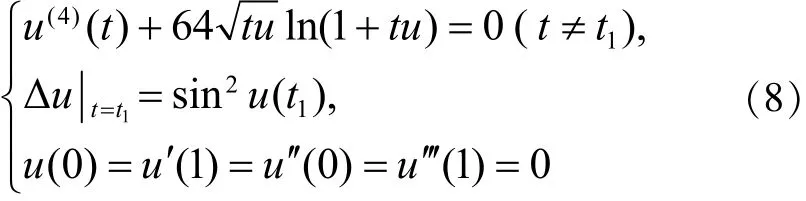
［1］FENG H Y，JI D H，GE W G.Existence and Uniqueness of Solutions for a Fourth-order Boundary Value Problem［J］.Nonlinear Anal，2009，70：3561-3566.

［2］HAN G D，LI F Y.Multiple Solutions of Some Fourthorder Boundary Value Problems［J］.Nonlinear Anal，2007，66：2591-2603.

［3］MA R Y.Existence of Positive Solutions of a Fourth-order Boundary Value Problem［J］.Appl Math Comput，2005，168：1219-1231.

［4］韦忠礼.四阶奇异边值问题的正解［J］.数学学报，1999（4）：715-722.

［5］郭大钧.非线性泛函分析［M］.2版.济南：山东科学技术出版社，2004：339-340.

【责任编辑王云鹏】

Existence of Solutions to Boundary Value Problems of Fourth-order Impulsive Differential Equations

ZHUANG Yaosen，LI Shanshan
（School of Mathematics and Information Science，Xinxiang University，Xinxiang 453003，China）

In this paper，a fourth-order differential equation boundary value problem with pulse was discussed.By means of fixed point index theorem，two nonnegative solutions of this problem under appropriate conditions were proved to be existed.

boundary value problem with pulse；fixed point index theorem；nonnegative solution

0175

A

2095-7726（2015）09-0001-03

2015-06-08

庄乐森（1980-），女，河南新乡人，硕士，研究方向：非线性泛函分析。