沂蒙山区降雨侵蚀力空间分布推算方法

杨韶洋,刘霞,姚孝友,吴迪,张荣华,齐斐,张洪达

(1.山东省土壤侵蚀与生态修复重点实验室,山东农业大学林学院水土保持系,271018,山东泰安;2.美国密西西比州立大学森林资源系,39759,美国密西西比州斯塔克维尔;3.南京林业大学林学院,210000,南京;4.水利部淮河水利委员会水土保持监测中心站,233001,安徽蚌埠)

降雨侵蚀力(rainfall erosivity)是评价降雨引起土壤侵蚀潜在能力的一个动力指标[1],研究区域降雨侵蚀力空间插值方法,对提高预测精度,了解区域降雨侵蚀力空间分布规律具有重要意义。空间插值方法主要有确定性插值方法(反距离权重插值、样条曲线插值)和地统计插值方法(克里格插值),其中,地统计插值方法既充分考虑了样本点的方向、位置和距离,又能够对数据中存在的趋势和异向性进行处理,选出最优、最适合的模型进行拟合[2]。因此,近年来国内外诸多学者采用地统计插值方法中的普通克里格法(Ordinary Kriging)对不同区域降雨侵蚀力的空间分布特征进行了研究[3-8],并取得了一定的成果;但在土壤养分、温度空间预测的相关研究探索中发现,由多元线性回归和普通克里格法结合而成的回归克里格法(Regression Kriging)比普通克里格法更能提高空间预测精度[9-15],而目前应用回归克里格法对降雨侵蚀力空间分布特征的研究鲜见报道。

笔者借助沂蒙山区88个雨量站点1980—2010年日降水数据和降雨侵蚀力日雨量公式,计算站点年均降雨侵蚀力,采用回归克里格法和普通克里格法对沂蒙山区降雨侵蚀力进行空间插值预测,探讨不同插值方法对降雨侵蚀力空间预测精度的影响,并对沂蒙山区降雨侵蚀力及其空间分布特征进行研究,以期为北方土石山区尤其是鲁中南低山丘陵区降雨侵蚀力研究及区域水土流失定量评价提供技术支撑。

1 研究区概况

沂蒙山区位于淮河流域北部、山东省的中南部,属北方土石山区,面积3万2 571.29 km2,涉及27个县(市、区)。属半湿润暖温带季风气候,年均气温12～14℃,年均降水量为700～900 mm,主要集中在夏季汛期(6—9月),汛期降雨量为592 mm,占全年降水量的71.3%;河流水系为沂沭泗河水系,总长度2 586 km。地貌类型以山地丘陵为主,山丘区面积占63%;主要土壤类型有棕壤、褐土、潮土、砂浆黑土、粗骨土;地带性植被属暖温带阔叶林带,森林植被主要有油松(Pinus tabulaeformis),赤松(Pinus densiflora)、侧柏(Platycladus orientalis)刺槐(Robinia pseudoacacia)、麻栎(Quercus acutissima)等,灌草植被主要有黄荆(Vitex negundo)、酸枣(Ziziphus jujuba)、结缕草(Zoysia japonica)等。

2 材料与方法

2.1 数据来源与处理

以沂蒙山区88个雨量站点(图1)1980—2010年日降水资料为基础数据源,采用章文波等[16]日雨量修正模型[17](式(1)和式(2)),计算得到年均降雨侵蚀力实算值,并统计各站点年均降雨量、年均汛期(6—9月)降雨量及年均侵蚀性降雨量(日降雨量≥12 mm)。基于ArcGIS地统计分析功能,采用普通克里格法获得年均降雨量、年均汛期降雨量和年均侵蚀性降雨量插值图。

年均降雨侵蚀力计算公式为:

式中:R半月k为第 k 半月的降雨侵蚀力,MJ·mm/(hm2·h·a);Pdij为第i年第k半月第j日≥12 mm的日降雨量;α、β为回归系数;Pd12为日降雨量≥12 mm的日平均值,mm;Pdl表示统计时段内第l日≥12 mm的日降雨量;j=1,2,…,m为第i年第k半月日降雨量≥12 mm的时间,d;i=1,2,…,N为时间,a;l=1,2,…,n为统计时段内所有日降雨量≥12 mm的时间,d。为多年平均年降雨侵蚀力,MJ·mm/(hm2·h·a);k=1,2,…,24,表示1年24个半月。

2.2 降雨侵蚀力空间插值方法

2.2.1 普通克里格插值 以年均降雨侵蚀力为区域化变量,半方差函数为分析工具,对插值点区域化变量的取值进行线性无偏最优估计[18-19]。

2.2.2 回归克里格插值 以年均降雨侵蚀力为目标变量、降雨特征值为辅助变量建立回归方程,利用回归方程对趋势项进行预测,计算趋势项残差并其进行普通克里格插值,最终将趋势项与残差项进行空间相加得到目标变量预测值。

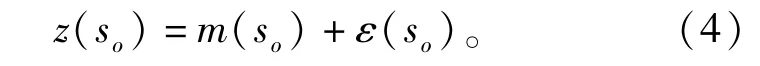
式中:z(so)为未知点so目标变量,即降雨侵蚀力回归克里格预测值;m(so)为趋势项,即降雨侵蚀力回归方程预测值,通过线性回归进行拟合;ε(so)为残差项(降雨侵蚀力实算值-回归预测值),利用普通克里格插值预测;so为未知点,o=1,2,…,n。

2.3 不同方法预测精度评价

随机抽取13个站点作为数据精度验证子集,验证剩余75个站点的插值预测结果精度。通过比较验证站点的实算值与预测值,采用式(5)和(6)计算平均绝对误差和均方根预测误差[20],并以均方根误差作为指标,利用式(7)计算相对精度改进值[21],评价预测精度。

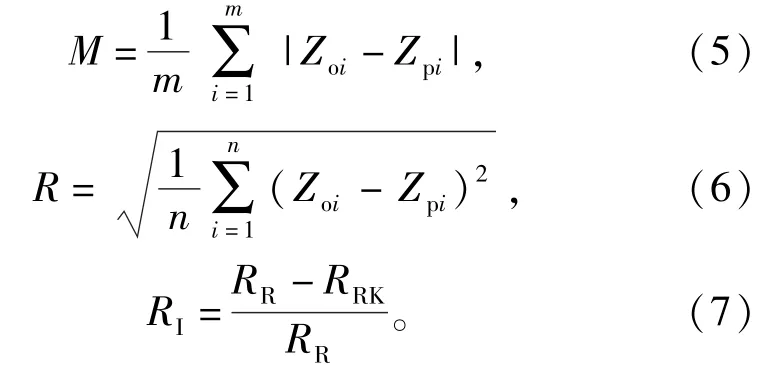
式中:M为平均绝对误差;m为验证数据子集采样点数目;Zoi、Zpi分别为雨量站点i的实算值和预测值;R为均方根预测误差;RI为回归克里格插值相对于普通克里格插值的相对精度改进值;RR为普通克里格插值的均方根预测误差值;RRK为回归克里格插值的均方根预测误差值。

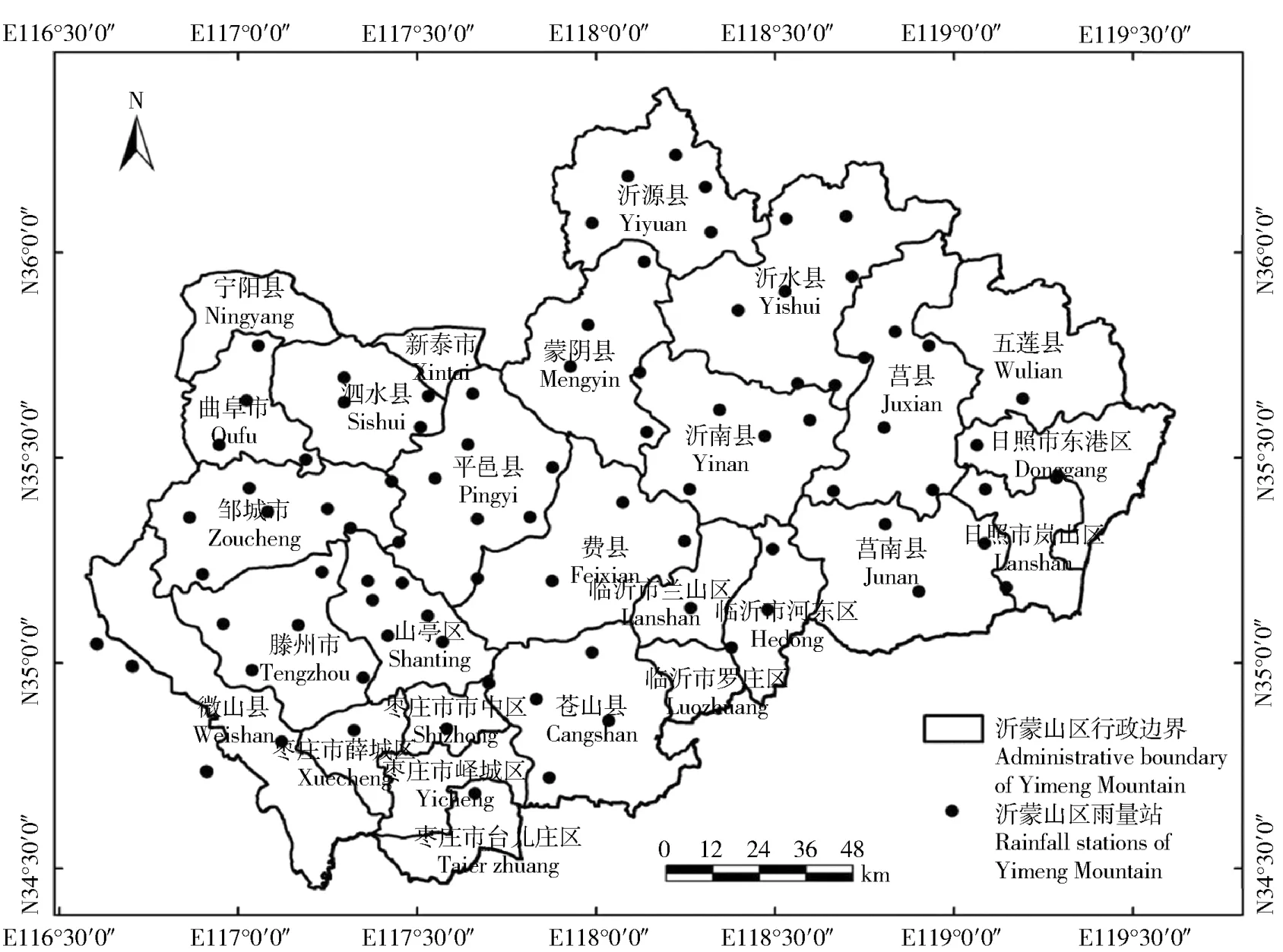
图1 沂蒙山区雨量站点分布图Fig.1 Distribution map of rainfall stations in Yimeng Mountain Area

2.4 空间分布差异性分析

根据降雨侵蚀力插值结果,按照同一分级标准分类( ＜3 300 MJ·mm/(hm2·h·a)(1 级),≥3 300 ～3 700 MJ·mm/(hm2·h·a)(2 级), ＞ 3 700 ～ 4 100 MJ·mm/(hm2·h·a)(3 级), ＞ 4 100 ～ 4 500 MJ·mm/(hm2·h·a)(4 级), ＞ 4 500 ～ 4 900 MJ·mm/(hm2·h·a)(5 级), ＞4 900 ～5 300 MJ·mm/(hm2·h·a)(6级)和 ＞5 300 MJ·mm/(hm2·h·a))(7 级),从小到大依次编号为1～7级。基于ArcGIS空间分析模块,叠加生成图谱和面积转移矩阵,分析不同插值方法降雨侵蚀力空间分布差异性。

3 结果与分析

3.1 降雨侵蚀力与降雨特征值

由表1可知,年均降雨侵蚀力均值为4 133.92 MJ·mm/(hm2·h·a);变化范围在 3 033.23 ～5 438.22 MJ·mm/(hm2·h·a)之间,标准差为567.59,变异系数达13.73%。根据反映离散程度变异系数的分级标准[22]可知,沂蒙山降雨侵蚀力属中等变异。

表1 沂蒙山区降雨侵蚀力统计特征值Tab.1 Rainfall erosivity statistical characteristics of Yimeng Mountain Area MJ·mm/(hm2·h·a)

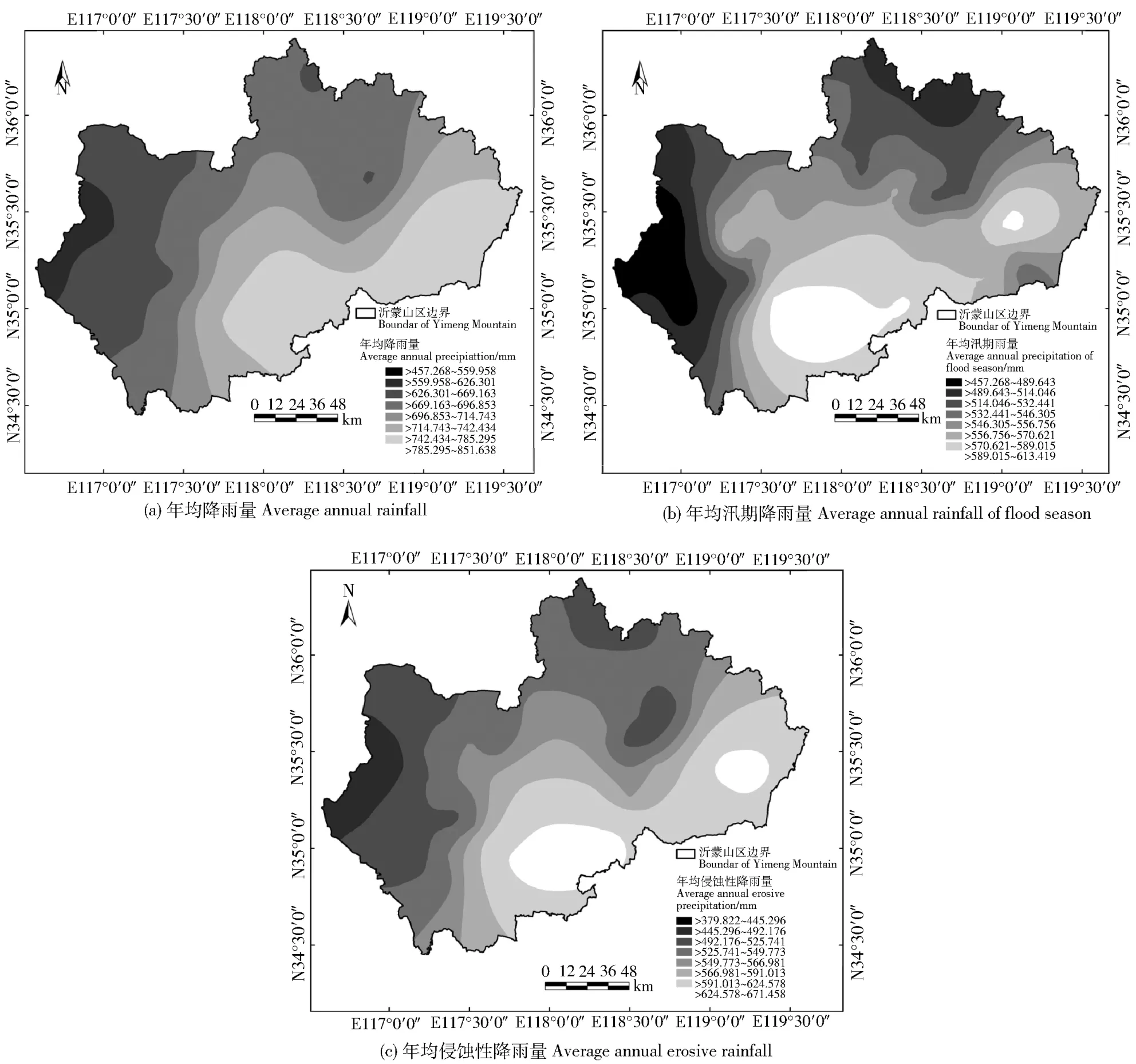
图2 沂蒙山区降雨特征值空间分布图Fig.2 Rainfall characteristics values distribution map of Yimeng Mountain Area

根据沂蒙山区降雨特征值空间分布图(图2)可知,年均降雨量、年均汛期降雨量以及年均侵蚀性降雨量的变化范围分别在457.27～851.64、457.27～613.42和379.82～671.46 mm之间,各降雨特征值在空间分布上存在差异性,整体上遵循从南向西北和东北2个方向逐渐递减的特征。

3.2 普通克里格插值分析

随机选取75个雨量点的年均降雨侵蚀力实算值作为区域化变量,采用普通克里格法插值生成年均降雨侵蚀力空间分布图(图3),分析可知,降雨侵蚀力均值为4 214.85 MJ·mm/(hm2·h·a),变化范围为3 293.30 ～5 271.71 MJ·mm/(hm2·h·a),其空间分布规律与降水特征值分布规律一致。但插值结果的均值、最大值和最小值与实算值分别相差80.93、166.51 和 260.07 MJ·mm/(hm2·h·a),表明普通克里格插值结果与实算值差异较大。

图3 沂蒙山区普通克里格法降雨侵蚀力空间分布图Fig.3 Rainfall erosivity map of the Ordinary Kriging method in Yimeng Mountain Area

3.3 回归克里克插值分析

3.3.1 降雨侵蚀力与降雨特征值相关性分析 降雨侵蚀力与各降雨特征值呈极显著相关(表2),其中与年均汛期降雨量相关性最高,相关系数达0.917,表明降雨侵蚀力随年均降雨量、年均汛期雨量和年均侵蚀性降雨量的增加而增大。年均降雨量与降雨侵蚀力的相关系数小于年均汛期雨量和年均侵蚀性降雨量,表明年均降雨量对降雨侵蚀力的影响小于年均汛期降雨量和年均侵蚀性降雨量。

3.3.2 回归预测模型 采用多元线性逐步回归的方法,基于上述75个插值站点各降雨特征值拟合计算降雨侵蚀力变化特征。方程拟合结果如下:

模型1:m=13.892x1-3 426.750,R2=0.839(P＜0.05);

表2 沂蒙山区降雨侵蚀力与降雨特征值相关性Tab.2 Correlations between the rainfall erosivity and rainfall characteristics of Yimeng Mountain Area

模型2:m=9.906x1+2.822x2-2 819.957,R2=0.888(P ＜0.05)。

式中:m为年均降雨侵蚀力回归方程预测值;x1为年均汛期降雨量;x2为年均侵蚀性降雨量。

从拟合方程来看,模型1与模型2均为逐步回归结果,且模型2的决定系数大于模型1;因此选择模型2作为最优拟合结果,进行降雨侵蚀力拟合计算。同时所选降雨特征值中,年均降雨量被剔除,说明虽然年均降雨量与降雨侵蚀力极显著相关,但其不能很好反映降雨侵蚀力的空间分布特征,而年均汛期降雨量和年均侵蚀性降雨量均被保留,说明二者是影响降雨侵蚀力空间预测的主要因素。

3.3.3 残差分析 由残差统计特征值(表3)可以看出,回归预测残差均值为 -0.37 MJ·mm/(hm2·h·a),变化范围在 -389.97 ～356.88 MJ·mm/(hm2·h·a)之间,残差值变化范围较大,存在较强的变异性。对预测残差进行半方差函数分析,结果(表4)表明,指数模型基台效应和均方根误差均小于其他2个模型,因此选取指数模型作为插值模型。降雨侵蚀力预测残差基台效应为25.73%,属中等空间相关性[23],表明年均汛期降雨量和年均侵蚀性降雨量作为结构因素是引起降雨侵蚀力空间变异的主要原因,而随机因素影响较小。

表3 沂蒙山区降雨侵蚀力回归预测残差统计特征值Tab.3 Regression prediction residual statistical characteristic values of rainfall erosivity of Yimeng Mountain Area

表4 降雨侵蚀力预测残差半方差函数模型及其参数Tab.4 Prediction residual semi variance function models and parameters of rainfall erosivity

3.3.4 插值结果分析 分析年均降雨侵蚀力插值分布图(图4)可知,采用回归克里格插值后降雨侵蚀力均值为4 176.55 MJ·mm/(hm2·h·a),变化范围为3 065.27 ～5 413.70 MJ·mm/(hm2·h·a),其空间分布规律与降雨特征值空间分布规律一致。插值结果的均值、最大值和最小值与实算值分别相差42.63、24.52 和 32.04 MJ·mm/(hm2·h·a),说明回归克里格插值结果与实算值相近。

表5 不同插值方法预测精度对比Tab.5 Precision comparation of different interpolation methods

3.4 不同插值方法对比分析

3.4.1 插值精度评价 采用剩余13个验证站点来比较2种插值方法的预测精度,从预测精度(表5)可知,回归克里格法的平均绝对误差(108.69)小于普通克里格法的平均绝对误差(250.22),同时各验证点绝对误差(图5)表明回归克里格法要明显低于普通克里格法;对比均方根误差可知,回归克里格法均方根误差为139.11,明显小于普通克里格法的300.05,回归克里格法相对精度改进值为53.64%,说明回归克里格插值结果比较理想,其预测精度高于普通克里格插值。

3.4.2 空间分布差异性分析 根据降雨侵蚀力插值分级结果空间叠加图谱(图6)和降雨侵蚀力插值图层空间叠加转移矩阵(表6)所示,2种方法插值结果中,降雨侵蚀力等级一致的面积为2万4 794.51 km2,占总面积的76.12%,即叠加图谱中的白色区域,说明2种插值方法的降雨侵蚀力空间分布规律具有一致性;但进一步分析发现,2种方法插值结果在各级别上存在差异,其中:普通克里格插值结果分级中缺少第7级,而回归克里格插值结果中存在,且普通克里格插值结果的第6级中有1 285.58 km2在回归克里格结果中属于第7级,即叠加图谱中的正方形网格区;其次普通克里格插值结果的第1级面积仅为1.42 km2,且在回归克里格中属于第2级,即变化图谱中的竖线区,而回归克里格插值结果的第1级面积为372.67 km2,在普通克里格中属于第2级,即叠加图谱中的斜网格区。

图4 沂蒙山区回归克里格法降雨侵蚀力空间分布图Fig.4 Rainfall erosivity map of the Regression Kriging method in Yimeng Mountain Area

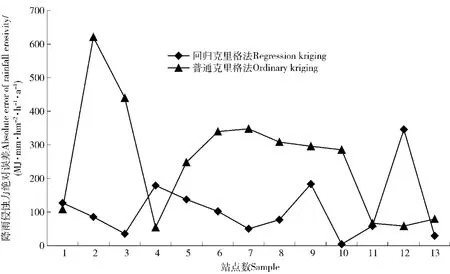
图5 不同方法预测绝对误差分析图Fig.5 Prediction absolute error analysis chart of different interpolation methods

上述分析说明,虽然2种插值结果在空间分布规律上具有一致性,但普通克里格插值结果在各降雨侵蚀力级别中分布不完全,对局部变异特别是极值区体现不够充分,而回归克里格插值结果除了在数值上与降雨侵蚀力实算值接近外,其插值结果对于局部变异体现更为精确。从空间分布的情况来看,回归克里格插值结果更为接近现实情况,说明其对于空间分布预测的效果更好。

图6 不同方法降雨侵蚀力插值分级结果空间叠加图谱Fig.6 Spatial overlay map of rainfall erosivity classify results of different interpolation methods

表6 不同方法降雨侵蚀力插值图层空间叠加转移矩阵Tab.6 Area transfer matrix of the rainfall erosivity interpolation maps of different methods km2

3.5 降雨侵蚀力空间分布特征

根据沂蒙山区降雨侵蚀力回归克里格插值图(图4)所示:沂蒙山区年均降雨侵蚀力最小值出现在沂源县北部,最大值出现在苍山县中部,降雨侵蚀力整体呈现由南向西北和东北2个方向递减的特征,这与区域内降雨特征值分布规律一致。同时,在邹城东部和莒县东部存在2个高值中心,在沂南东北部和山亭区北部存在2个低值中心。由各县降雨侵蚀力分布特征(表7)可知:沂源县降雨侵蚀力均值最小为3 449.60 MJ·mm/(hm2·h·a),临沂市罗庄区降雨侵蚀力均值最大为5 324.29 MJ·mm/(hm2·h·a),除沂源县外微山县、沂水县、莒县和蒙阴县等9县降雨侵蚀力均值低于 4 000 MJ·mm/(hm2·h·a);邹城市、新泰市、五莲县和泗水县等9县,降雨侵蚀力均值在 4 000 ～4 500 MJ·mm/(hm2·h·a)之间;日照市岚山区、枣庄市台儿庄区、费县等6县,降雨侵蚀力均值在4 500 ～5 000 MJ·mm/(hm2·h·a)之间;临沂市兰山区、苍山县和罗庄区降雨侵蚀力均值大于5 000 MJ·mm/(hm2·h·a) 。

沂蒙山区降雨侵蚀力变异系数为12.01%,说明沂蒙山区降雨侵蚀力在空间分布属中等变异;但各县(市、区)除邹城市属中等变异外,其他各县变异系数均小于10%,属弱变异,说明邹城市降雨侵蚀力的空间变异性大于其他各县,主要原因是邹城市存在降雨侵蚀力极值中心。

表7 沂蒙山区各县降雨侵蚀力统计特征值Tab.7 Rainfall erosivity statistical characteristics of different counties in Yimeng Mountain Area MJ·mm/(hm2·h·a)

4 结论与讨论

1)回归克里格法插值预测结果与降雨侵蚀力实算值相近。与普通克里格法相比,回归克里格法的相对精度改进值为53.64%;虽然2种方法降雨侵蚀力插值结果在空间分布规律上具有一致性,但回归克里格插值结果对降雨侵蚀力分布规律的描述更为精确。

2)沂蒙山区降雨侵蚀力与降雨特征值多元线性逐步回归结果表明,年均降雨量并不是影响降雨侵蚀力空间分布的主要因素,年均汛期雨量和年均侵蚀性雨量等结构因素是影响降雨侵蚀力空间分布的主要因素,而随机因素对降雨侵蚀力的影响较小。

3)沂蒙山区降雨侵蚀力在空间分布上遵循从南向西北和东北2个方向逐渐递减的分布规律,与区域内降雨分布规律一致。沂蒙山区27个县(市、区)中,除邹城市外其他各县降雨侵蚀力在空间分布上均属于弱空间变异,且各县降雨侵蚀力空间变异性均小于沂蒙山区。

本研究采用回归克里格法仅对沂蒙山区降雨侵蚀力进行了空间预测,并与普通克里格法对比分析,但回归克里格法是否在其他区域也具有相同的效果尚不明确;同时本研究仅对降雨特征值与降雨侵蚀力相关性进行分析,对于降雨特征值如何影响降雨侵蚀力还有待进一步研究。虽然沂蒙山区各县(市、区)降雨侵蚀力在空间分布上属于弱变异性,但县域间降雨侵蚀力存在明显差异;因此各县应根据区域降雨侵蚀力分布特点及实际情况合理进行水土流失预防和治理。沂蒙山区各县降雨侵蚀力空间变异性均小于沂蒙山区,说明降雨侵蚀力空间变异可能与区域尺度有关,如何确定不同区域尺度对降雨侵蚀力空间变异的影响还有待深入研究。