桥面板混凝土理论厚度对组合梁桥收缩徐变的影响分析

吴 俣,邓青儿,于 洋

(上海市政工程设计研究院,上海市 200092)

桥面板混凝土理论厚度对组合梁桥收缩徐变的影响分析

吴 俣,邓青儿,于 洋

(上海市政工程设计研究院,上海市 200092)

以《公预规》为依据,讨论了组合梁桥中桥面板不同理论厚度计算方法得到的收缩应变和徐变系数间的差别,提出了采用随时间变化理论厚度计算收缩徐变参数的方法。接着,以一座2×75 m连续组合梁桥为背景工程,建立有限元模型,针对不同桥面板混凝土理论厚度计算了结构收缩徐变引起的变形和应力。结论表明目前普遍应用的以施工铺装前截面计算桥面板混凝土理论厚度的方法得到的收缩徐变效应普遍偏大,但组合梁钢结构的部分计算结果偏于不安全。

组合梁;理论厚度;收缩;徐变

0 引言

式中:Ac——构件截面面积;

u——构件与大气接触的周边长度。

虽然我国现行《公路钢筋混凝土及预应力混凝土桥涵设计规范 (JGT D62-2004)》(以下简称《公预规》)给出了明确的公式,但对组合梁桥来讲,参数“u:构件与大气接触的周边长度”一项定义不够明确,目前,“u”的计算方法各有不同,主要体现在以下两方面:断面上,钢箱梁内部一般在施工结束后会密封,混凝土周长是否与外部取相同权重计算;过程上,铺装施工后覆盖了混凝土桥面板表面,这一部分是否仍计入与大气接触长度。

本文为了解该参数不同取值对设计的影响,

组合结构桥梁断面由钢结构及混凝土桥面板构成。桥面板混凝土收缩徐变是影响组合梁桥受力性能的重要因素之一。混凝土作为一种复合多相的人工土建筑材料,其收缩徐变性能的影响因素众多。基于混凝土收缩徐变的物理机理,普遍认为混凝土收缩徐变特性是由混凝土原材料及配合比、构件的尺寸、环境、相对湿度和温度等因素所共同决定的。凡是收缩值大的混凝土,其徐变值一般也大。

构件理论厚度在有些参考资料中又将其称为有效厚度,是反映构件尺寸、衡量构件与大气接触情况的一个参数,其计算公式如下:以一座2×75 m连续组合梁桥为背景工程,采用不同方法计算桥面板混凝土理论厚度并进行对比分析,了解理论厚度的取值对组合梁桥收缩徐变的影响。

2×75 m连续组合梁桥的基本情况如下:箱梁采用槽形钢梁+现浇混凝土桥面板结构。箱梁宽8 m,两侧悬臂长度各7.025 m;桥面板采用现浇C50混凝土,宽度22.05 m,见图1所示。

1 参数选取

根据目前计算理论厚度常见的几种观点,本文考虑以下三种算法,文中所选取的背景工程对应的桥面板混凝土理论厚度如表1所列。

本文依照《公预规》上提出的混凝土收缩应变和徐变系数计算公式,分析不同理论厚度值对计算结构变形、应力的影响程度。

2 桥面板混凝土理论厚度对收缩应变、徐变系数的影响分析

图2、图3展示了不同理论厚度的混凝土徐变系数和收缩应变随时间发展关系。

由图2、图3可知,构件理论厚度对收缩徐变的影响都是时间的函数,初期影响较大,之后逐渐减小。且其对收缩应变的影响大于对徐变系数的影响。

考虑到施工铺装前后构件的理论厚度发生了变化,徐变系数的终极值和随时间的函数都发生了变化,可考虑根据施工过程改变混凝土徐变系数中理论厚度的值,获得较为准确的徐变系数随时间的函数。

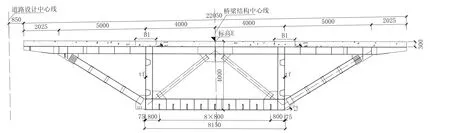
图1 2×75 m连续组合梁桥标准断面图

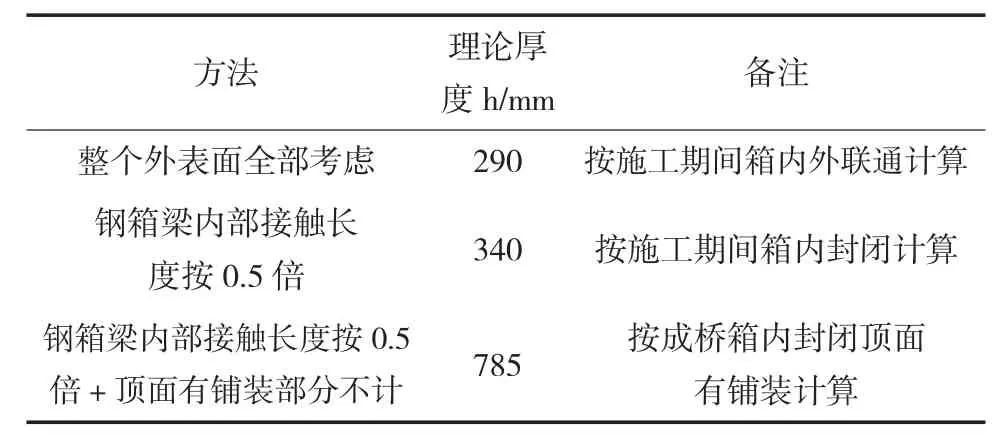
表1 三种计算桥面板混凝土理论厚度的方法及其数值一览表

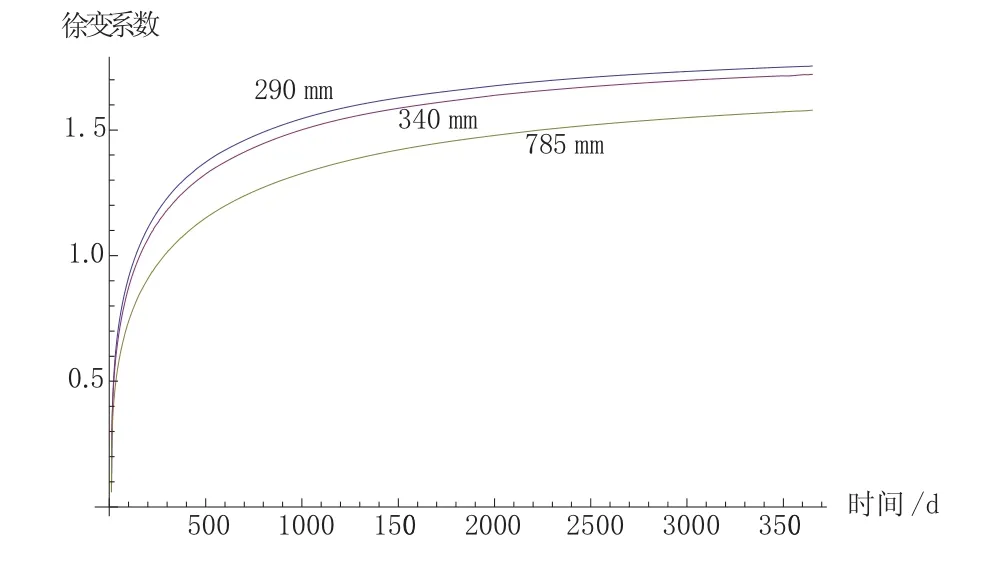
图2 不同理论厚度的混凝土徐变系数随时间发展关系曲线图

图3 不同理论厚度的混凝土收缩应变随时间发展关系曲线图

《公预规》中混凝土徐变系数是加载龄期tO、环境年平均相对湿度RH、理论厚度h,以及混凝土28 d立方体抗压强度fcm的函数,可表示为:

式中:φ(t，t0)——加载龄期为t0,计算考虑龄期为t时的混凝土徐变系数;

φ0——名义徐变系数;

βc——加载后徐变随时间发展的系数。

设铺装施工前混凝土桥面板理论厚度为h1,施工后为h2,施工铺装时混凝土龄期为tp(tp＞t0),那么在施工铺装前,徐变系数计算时取理论厚度为h1,施工铺装后,徐变系数按照理论厚度为h2的徐变系数曲线发展,最终终极值介于理论厚度为h1和h2的值之间,即:

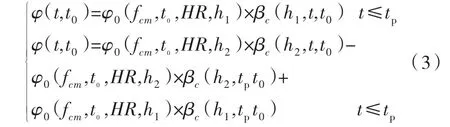
h1=290 mm,h2=785 mm,tp=30 d、45 d、60 d、75 d的徐变系数与h=290 mm和h=785 mm的徐变系数,如图4所示和表2所列。

图4 理论厚度随时间变化的混凝土徐变系数随时间发展关系曲线图

表2 理论厚度随时间变化的混凝土10 a徐变系数一览表

由图4及表2可知,考虑桥面板混凝土理论厚度变化、分段计算徐变系数对徐变的发展和终极值计算都有一定影响。混凝土浇筑和铺装施工间的间隔越长,混凝土徐变系数越接近于h=hl的徐变系数,反之,则接近于h=h2的徐变系数。从图4中可明显地看出,徐变曲线初期增长极其迅速,大约100 d后增速逐渐减缓,因此,施工铺装时混凝土已发生了相当大的徐变,造成理论厚度发生改变的徐变曲线更接近h=hl的徐变曲线。从表2还可以看出,tp=75 d时,徐变系数终极值与h=hl的终极值相差 0.8%,即使 tp=30 d,也仅相差3.3%,说明tp变化对徐变终极值影响很小,可忽略不计。

收缩应变中考虑理论厚度随时间变化的方法与徐变相同,这里不再进行推导,直接列出结果:

h1=290 mm,h2=785 mm,tp=30 d、45 d、60 d、75 d的收缩应变与h=290 mm和h=785 mm的收缩应变如图5所示和表3所列。

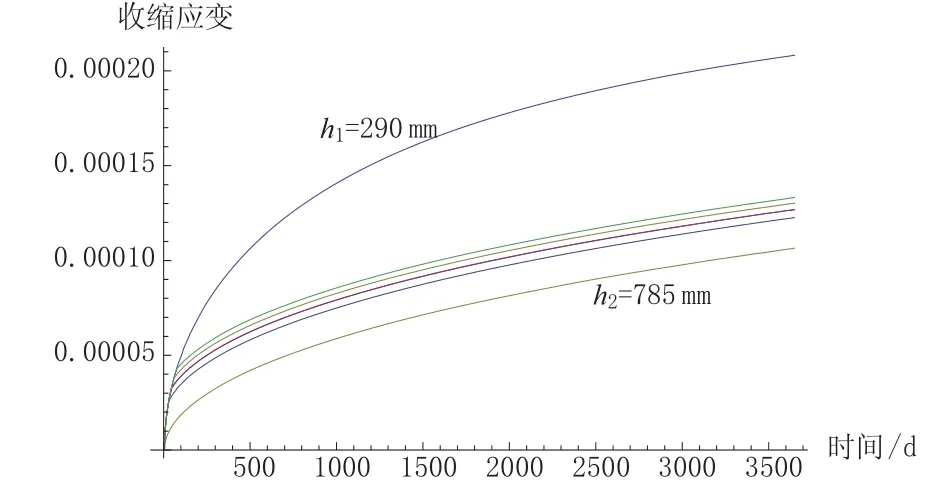
图5 理论厚度随时间变化的混凝土收缩应变随时间发展关系曲线图

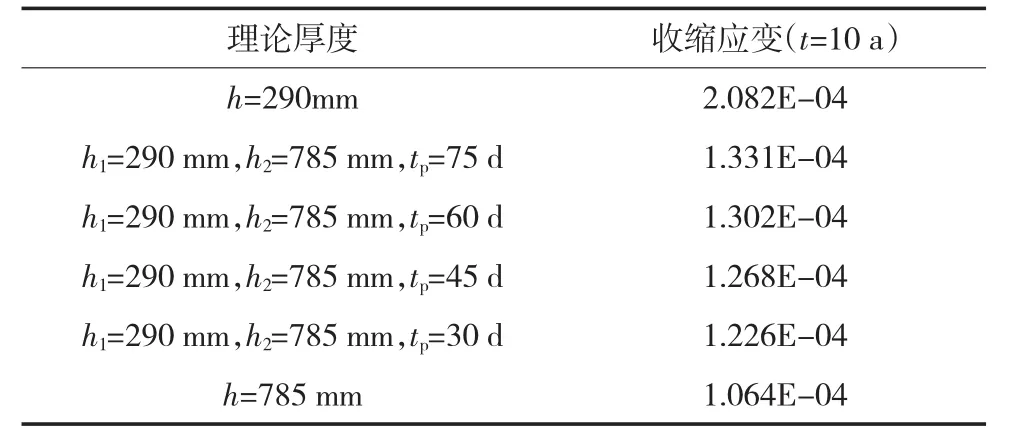
表3 理论厚度随时间变化的混凝土10 a收缩应变一览表

由图5和表3可知,考虑混凝土理论厚度变化、分段计算收缩应变对收缩的发展和终极值计算影响较大。混凝土浇筑和铺装施工间的间隔越长,混凝土收缩应变越接近于h=h1的收缩应变,反之,则接近于h=h2的收缩应变。从图5中可明显地看到,收缩应变与徐变系数的发展规律不同,收缩曲线前期比徐变曲线平缓,前期较长一段时间一直保持着较快的增长,大约400 d后增速才明显降低,前期几十天的收缩值占终极值的比例不是很大,因此,理论厚度改变后,收缩应变发展相对更接近于h=h2的收缩应变曲线,但与h=h2的收缩应变曲线仍相差20%左右。从表3还可以看出, tp=75 d时,徐变系数终极值与h=h1的终极值相差25.1%,即使tp=30 d,也相差15.2%,说明tp变化对收缩终极值的影响较大,其影响不可忽略。

以往对组合梁桥的徐变分析,混凝土桥面板的理论厚度一般按照铺装施工前的截面计算,即取h=h1。由以上分析可知,该方法对徐变系数值的计算偏大,但总体偏差较小,一般偏于安全;对收缩应变值的计算结果也偏于安全,但偏差较大。

3 桥面板混凝土理论厚度对结构变形和应力的影响分析

3.1 对变形的影响分析

从之前的分析来看,桥面板混凝土理论厚度对于收缩应变值的影响很大,对徐变系数值的影响小一些。为进一步分析其对结构最终变形和受力的影响,建立背景工程的MIDAS模型,考虑施工过程中桥面板混凝土理论厚度变化的影响,在施工过程中改变混凝土桥面板的理论厚度,对比分析其对主梁收缩徐变位移的影响。按背景工程实际施工流程,取:h1=290 mm,h2=785 mm,tp=70 d。图6和图7为不同桥面板混凝土理论厚度取值和考虑变理论厚度计算的主梁跨中徐变引起的位移和收缩引起的位移随时间的变化规律,表4列出了成桥10 a的值。

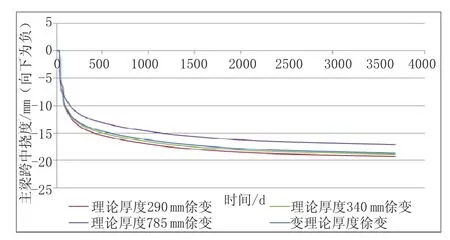
图6 不同理论厚度情况下主梁徐变位移随时间变化曲线图

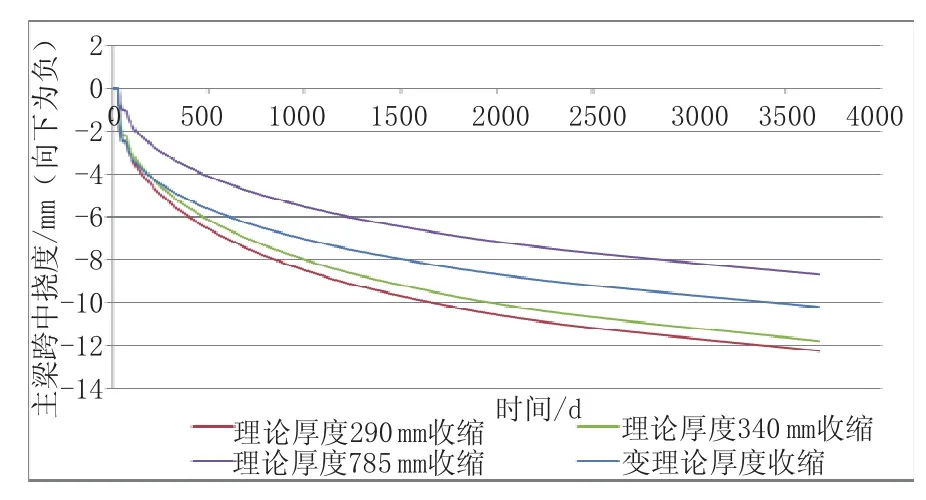
图7 不同理论厚度情况下主梁收缩位移随时间变化曲线图

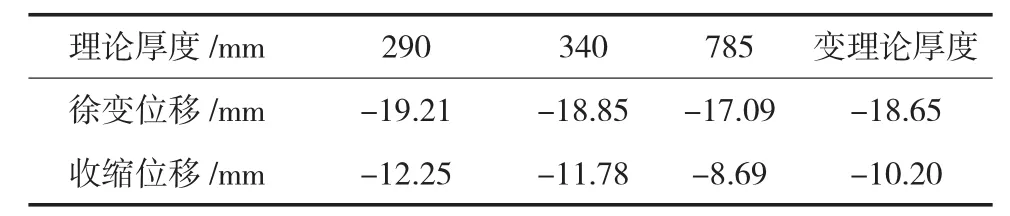
表4 考虑理论厚度变化的成桥10 a收缩徐变引起的位移对比一览表

考虑理论厚度变化的位移计算结果与之前分析一致,考虑理论厚度变化后徐变位移有所变化,但幅度不大,接近于h=290 mm的徐变位移(相差约2.92%)。收缩变化明显,其10 a收缩位移的计算结果在h=290 mm和h=785 mm的结果之间,且相对接近于h=785 mm的值。

3.2 对钢梁应力的影响分析

为与收缩徐变产生的应力形成数量概念上的对比,这里先列出成桥10 a钢梁在永久荷载作用下的应力(活载等其它可变荷载影响较小,暂不考虑),见图8、图9所示。

图8 成桥10 a钢梁上缘应力曲线图

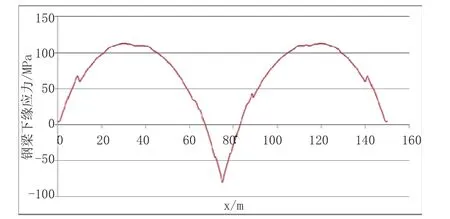
图9 成桥10 a钢梁下缘应力曲线图

图10～图13为主梁桥面板混凝土按不同理论厚度计算时,成桥10 a徐变和收缩引起的钢梁上下缘应力,受拉为正。其中,变理论厚度均指按背景工程实际施工流程,取h1=290 mm,h2=785 mm, tp=70 d计算的值。

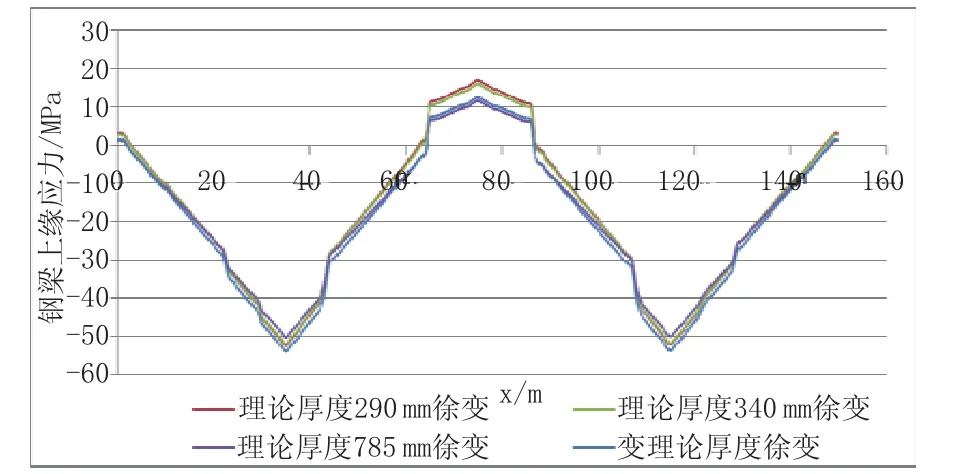
图10 不同理论厚度成桥10 a钢梁上缘徐变应力曲线图

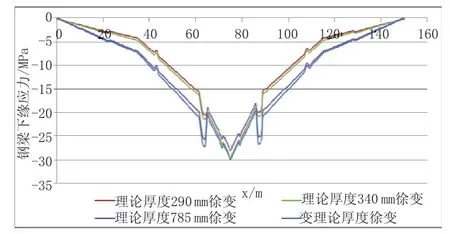
图11 不同理论厚度成桥10 a钢梁下缘徐变应力曲线图

图12 不同理论厚度成桥十年钢梁上缘收缩应力曲线图

图13 不同理论厚度成桥十年钢梁下缘收缩应力曲线图

从图10～图13中可以看出,采用常理论厚度计算,取h=785 mm与取h=290 mm相比,钢梁上缘徐变应力最大变化量位于中支点,拉应力减小约5.6 MPa,下缘徐变应力最大变化量在跨中附近,压应力增大约4.9 MPa;上缘收缩应力的最大变化值发生在边支点,压应力减小18 MPa,下缘收缩应力的最大变化值发生在距中支点约15 m处,压应力减小20.9 MPa。由数据可以看出,采用不同理论厚度计算收缩徐变得到的钢梁应力差别很大,特别是收缩应力,相差超过20 MPa。有必要按照结构理论厚度的实际变化情况分段计算徐变系数和收缩应变。从这些图中,还可容易看出,针对该桥,按照h=290 mm计算的钢梁收缩徐变应力偏大,与采用变理论厚度计算得到的钢梁应力相比,最多偏大16.7 MPa,如表5所列。

对比采用不同理论厚度的收缩徐变应力结果和成桥10 a钢梁应力图(图8、图9)可以看出,跨中略偏边支点位置的钢梁下缘为全桥拉应力最大的位置,拉应力约115 MPa,而该点收缩徐变应力均为负,若采用变理论厚度计算,该点成桥10 a拉应力将增大15 MPa左右。显然,按照h=290 mm计算的钢梁收缩徐变应力虽然大部分位置偏大,但局部仍是偏于不安全的。

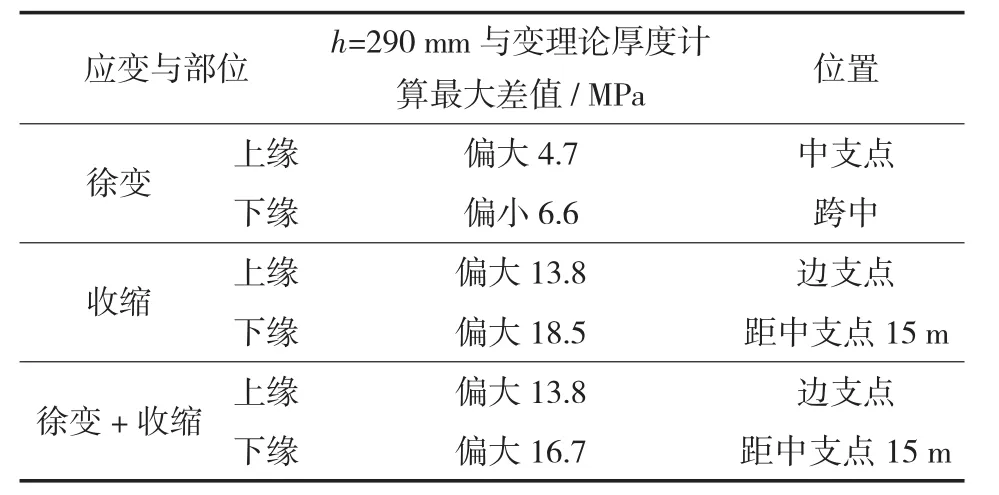
表5 考虑理论厚度变化的钢梁由桥面板混凝土收缩徐变引起的应力对比一览表

3.3 对桥面板混凝土应力的影响分析

为与收缩徐变产生的应力形成数量概念上的对比,这里先列出成桥10 a桥面板在永久荷载作用下的应力(活载等其它可变荷载影响较小,暂不考虑),见图14和图15所示。

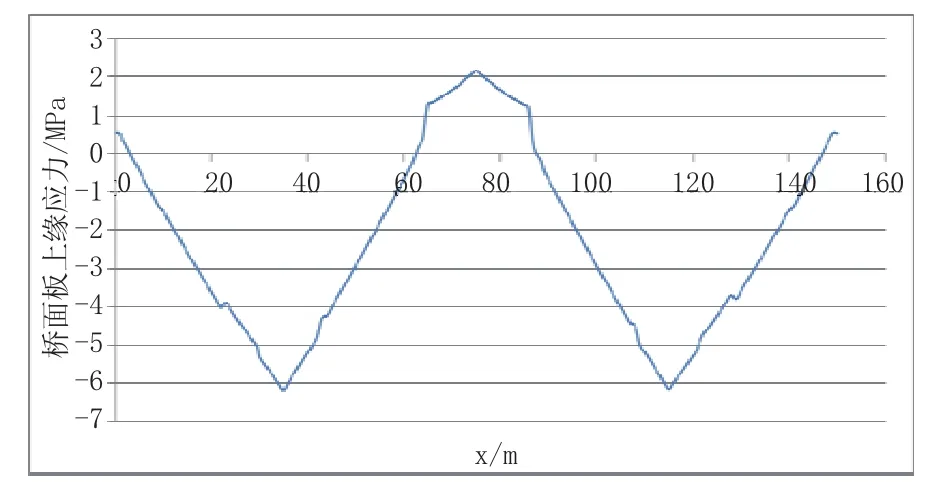
图14 成桥10 a桥面板上缘应力曲线图

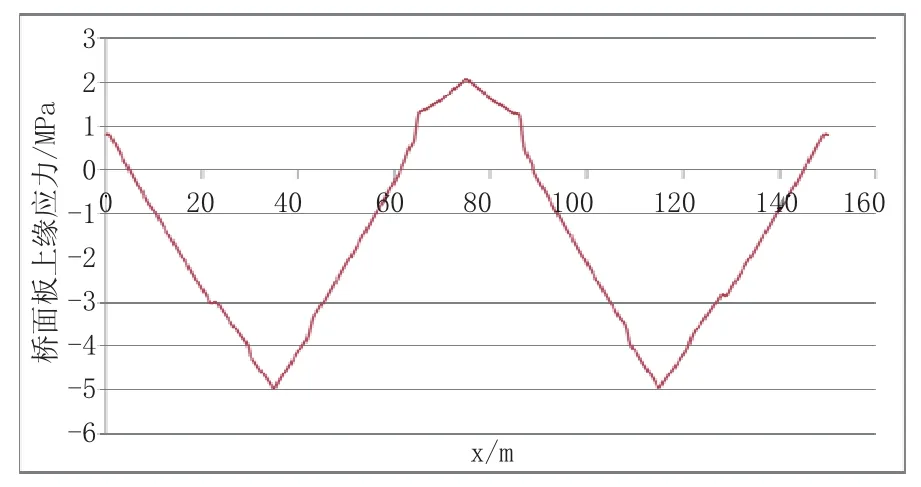
图15 成桥10 a桥面板下缘应力曲线图

图16～图19为主梁桥面板按不同理论厚度计算时,成桥10 a徐变和收缩引起的混凝土桥面板上下缘应力,受拉为正。

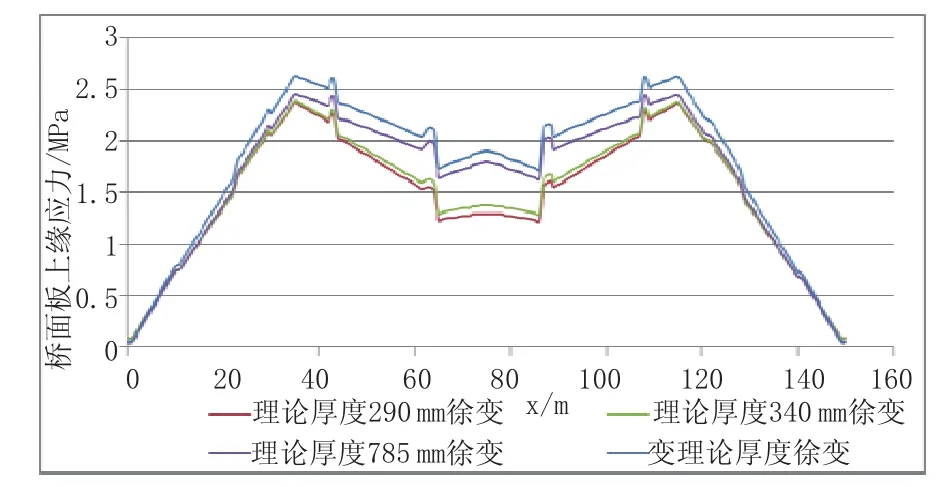
图16 不同理论厚度成桥10 a桥面板上缘徐变应力曲线图

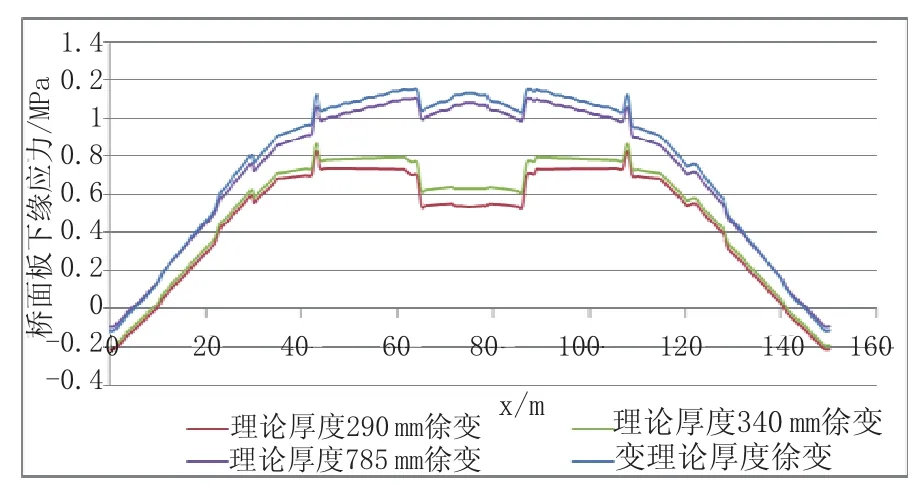
图17 不同理论厚度成桥10 a桥面板下缘徐变应力曲线图

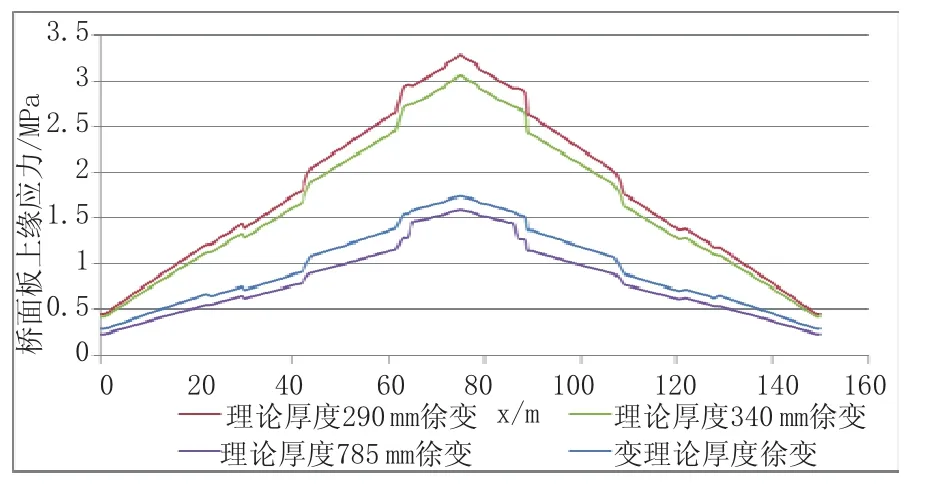
图18 不同理论厚度成桥10 a桥面板上缘收缩应力曲线图

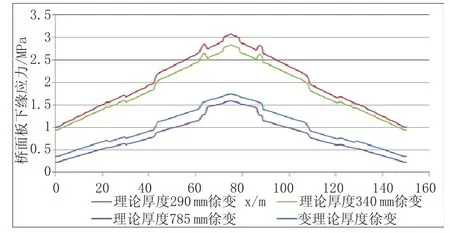
图19 不同理论厚度成桥10 a桥面板下缘收缩应力曲线图

从图16～图19中可以看出,采用常理论厚度计算,取h=785 mm与取h=290 mm相比,桥面板上缘徐变产生的拉应力最大增大了0.62 MPa,位置在跨中附近;下缘徐变产生的拉应力在两跨跨中之间的部分均增大了约0.60 MPa;上下缘收缩产生的拉应力均有明显减小,其中上缘减小1.6 MPa,下缘减小1.3 MPa,均位于中支点附近。即理论厚度增加造成徐变应力增大,收缩应力减小。收缩徐变综合起来考虑,上缘收缩徐变拉应力约降低了0.2～0.9 MPa,下缘降低0.4～0.7 MPa,总体来说,随着理论厚度增加,收缩徐变引起的拉应力减少,桥面板受力趋于有利。由数据可知,理论厚度的取值对收缩徐变应力影响很大,为准确分析收缩徐变对组合梁桥混凝土桥面板的影响,有必要根据施工实际情况变化桥面板理论厚度进行计算。

从这些图中,还可容易地看出,针对该桥,按照h=290 mm计算的混凝土收缩徐变应力偏大,与采用变理论厚度计算得到的桥面板应力相比,墩顶上缘拉应力相差最多,约0.9 MPa,如表6所列。

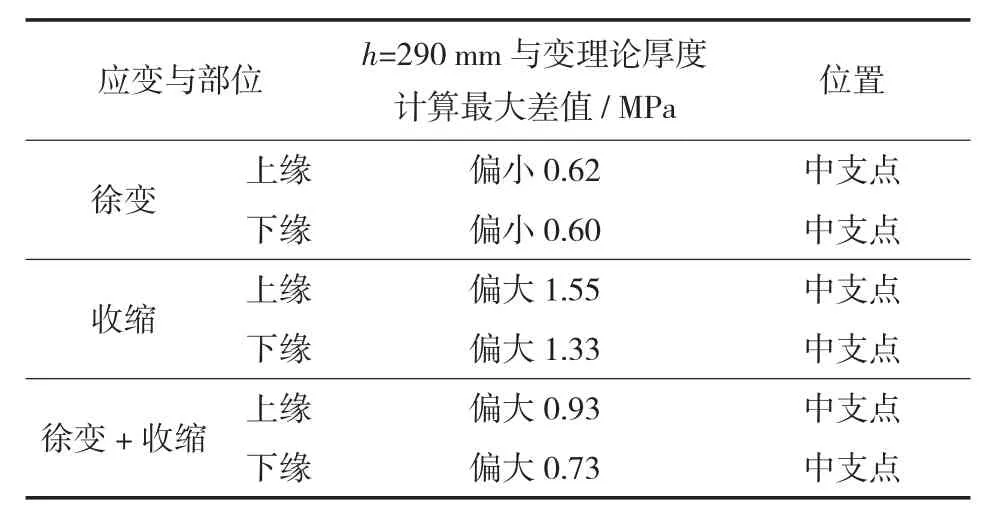
表6 考虑理论厚度变化的混凝土桥面板由收缩徐变引起的应力对比一览表

结合成桥10 a混凝土桥面板应力(见图14、图15)可知,桥面板跨中压应力约5～6 MPa,较小,墩顶拉应力约2 MPa,需通过配筋控制裂缝宽度。按照h=290 mm计算的收缩徐变拉应力偏大,按其结果设计是偏于安全的。

由以上分析可知,理论厚度的取值对结构变形和钢、混凝土的应力都有很大影响,采用h=290 mm与采用变化的理论厚度计算结果相比,普遍高估了收缩徐变引起的构件应力。对钢梁来说,收缩徐变应力偏大约15 MPa,由于在局部,收缩徐变对钢梁受力是有利的,计算结果偏大仍偏于不安全。对混凝土来说,收缩徐变拉应力偏大将近1 MPa,在中支点,计算的混凝土拉应力偏大,结果偏安全;在跨中,计算的混凝土压应力偏小,可能偏于不安全。

4 结论

组合梁桥面板理论厚度取值对收缩徐变的影响很大,且是时间的函数,初期影响较大,之后逐渐减小。对于施工过程中理论厚度发生变化的组合梁,目前多按照施工铺装前的截面计算理论厚度,一般来说其计算的收缩徐变效应偏大,对混凝土一般是偏安全的,但对钢梁可能偏于不安全。对于该桥,跨中近边支点处下缘拉应力低估约15 MPa左右,相对成桥时结构应力水平而言,这种影响不可忽略。

U448.21+6、U441

A

1009-7716(2015)03-0147-05

2014-11-24

吴俣(1987-),男,陕西安康人,硕士,助理工程师,从事钢和组合结构桥梁工程设计工作。