无信号T型交叉口的转弯速度特性及预测模型

杨 轸,郑 挺,肖松林

(同济大学交通运输工程学院,上海市 200092)

无信号T型交叉口的转弯速度特性及预测模型

杨 轸,郑 挺,肖松林

(同济大学交通运输工程学院,上海市 200092)

以舟山的一条二级公路为对象,采集车辆在自由形式状态下通过无信号T型交叉口的速度曲线,分析了车辆转弯通过无信号T型交叉口时的速度特性。重点分析了距离进口道线80 m处车速、进口道线处车速分布以及减速位置的分布,初步确立速度采集设备布设位置方案。通过选取距离交叉口进口道线80 m,50 m,30 m,20 m位置处的速度值,用指数函数、高斯函数、二次多项式函数和三次多项式函数分别预测进口道线处的速度,确定了最佳函数预测模型。

无信号T型交叉口;速度特性;函数拟合;函数预测模型

0 引言

近年来,交通安全预警技术已经成为交通相关学科中越来越热门的研究领域之一,而车速的特性分析以及预测模型的选取作为预警技术的基础直接影响预警技术的有效性和可靠性。车速的控制不当是造成交叉口事故的主要原因［1］。根据美国经验统计,假若驾驶员能提早0.5 s预知危险,就可减少50%的追尾和交叉口碰撞事故,正面碰撞事故减少30%;假若早1 s预知危险,就可避免90%的交通事故［2］。合理的预测模型建立能有效提高预测精度,从而大大降低事故发生率。

对于作为预警技术基础课题之一的交通信息采集技术,国内外都进行了相关的研究。如Haibo Chen、Mark Dougherty等人［3］,以神经网络模型对交通参数(交通量、速度等)的预测精度为目标,研究固定型检测器的布设密度对预测精度的影响,从而确定最佳检测器布设方案。K.S.ChA等人［4］,利用双层规划模型,充分考虑成本投入和行程时间检测精度,对道路网地埋型检测器的布设密度进行求解。同济大学储浩等人［5］,通过对快速路行程时间估算误差来解决埋入式检测器布设密度问题,结合成本的投入,得出检测器布设密度是有一个合理的范围的结论。总体来说,当前国内外对预警技术中的信息采集技术的研究多以交通量信息的采集为主,运用交通规划模型研究城市道路的信息采集设备的布设方法以及预警机制,而较少从函数模型的角度出发,通过采集速度信息研究一般公路无信号交叉口的预警有效性。

因此,本文试以一般公路中最普遍存在的3支无信号T型交叉口为对象,通过速度采集试验,研究分析速度采集设备的可行布设方案。从函数预测模型的角度出发,分析预测精度最优的函数模型。

1 实验设计

1.1 实验车辆与仪器

桑塔纳出租车、机动车非接触速度仪(即“五轮仪”,型号CTM-8C)、照相机、胶带、钢尺(5 m)。

1.2 实验驾驶员

选择8名年龄在28～42岁的职业出租车司机,其中男性5名,女性3名。

1.3 实验场景

选择浙江省舟山市内的一条二级公路为实验对象。设计时速60 km/h,双向2车道,路基宽度10 m,车道宽度7 m。路线是以舟山市委党校旁边的三官堂为起点,沿着三华线—S73号省道—定北线—三西线至干览镇,然后在干览镇调头,原路返回至三官堂。沿线选择7个无明显交通干扰、交通量小、几乎无纵坡度,且支路路宽相近的无信号T型交叉口(见图1 )。

1.4 实验样本采集方案

无信号交叉口的几何设计指标如主支路夹角以及视距条件等对速度数据特性均有影响［6］。本实验根据交叉口的几何特性,主要根据车辆行驶方式、行驶方向偏转角及视距条件分类采集车辆速度。图2为实验方案设计。

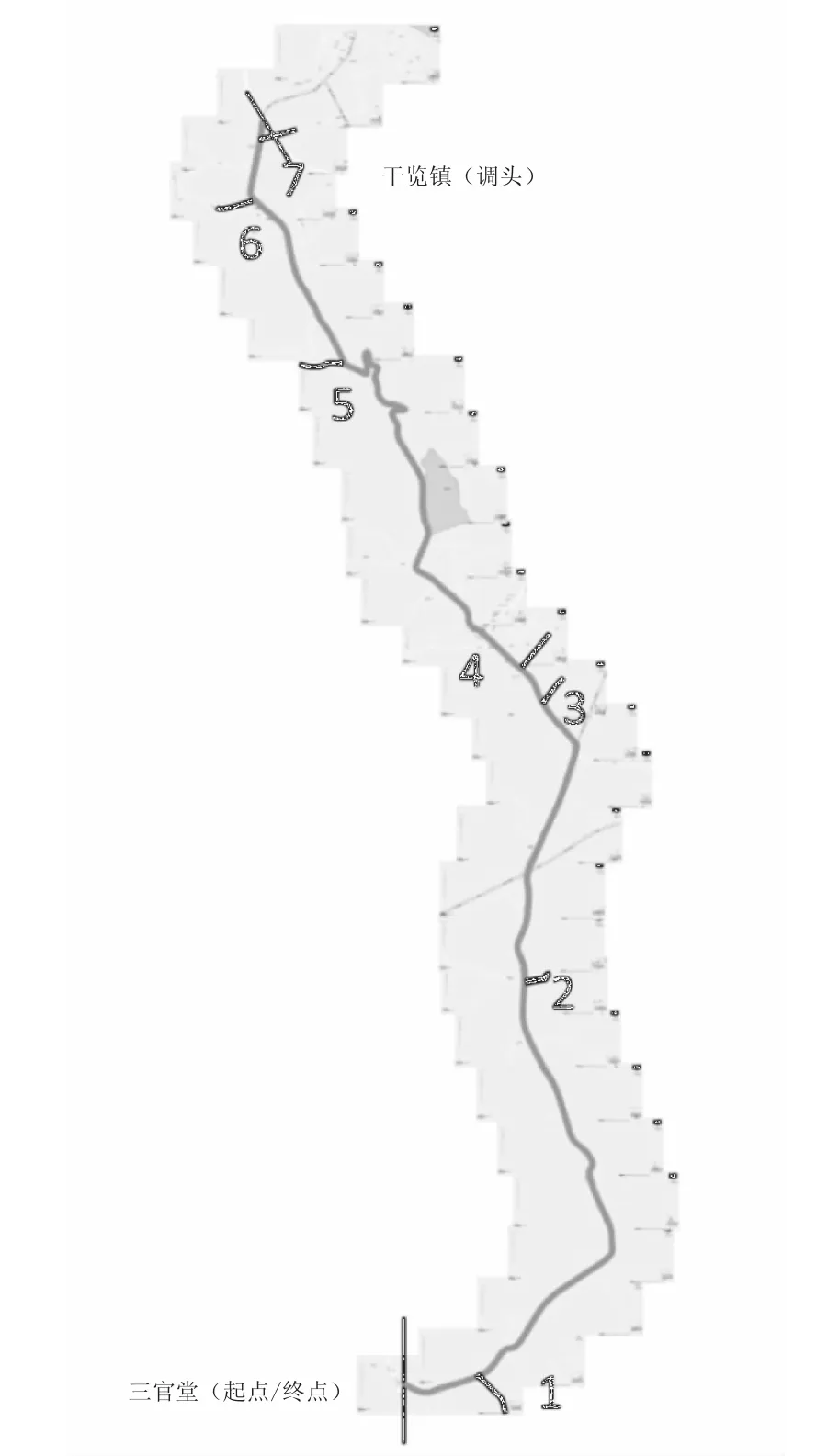
图1 试验线路及交叉口位置

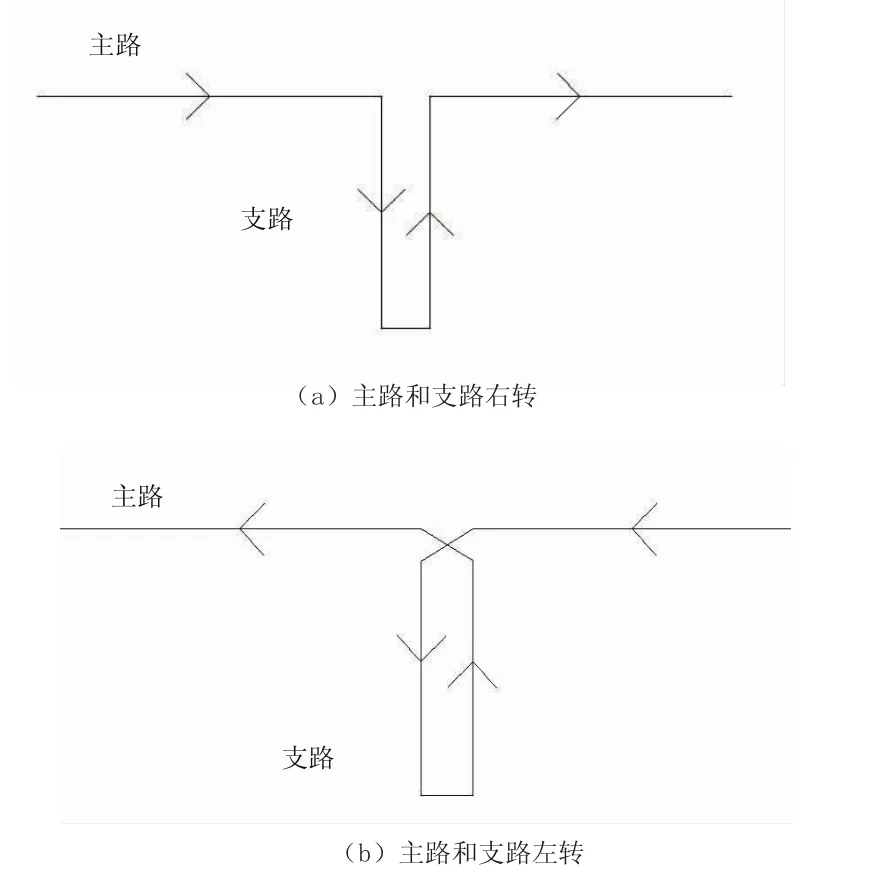
图2 实验方案设计

行驶方式根据行驶方向以及主干路的变化分为右转(主路进支路)、左转(主路进支路)、右转(支路进主路)、左转(支路进主路)4种,并且将行驶方向偏转角分为0°～75°、75°～105°、105°～180°三档。视距情况分为良好及不良两种。分别采集各类型的样本速度。根据以上分类方法,列表表示样本数据采集情况(见表1)。

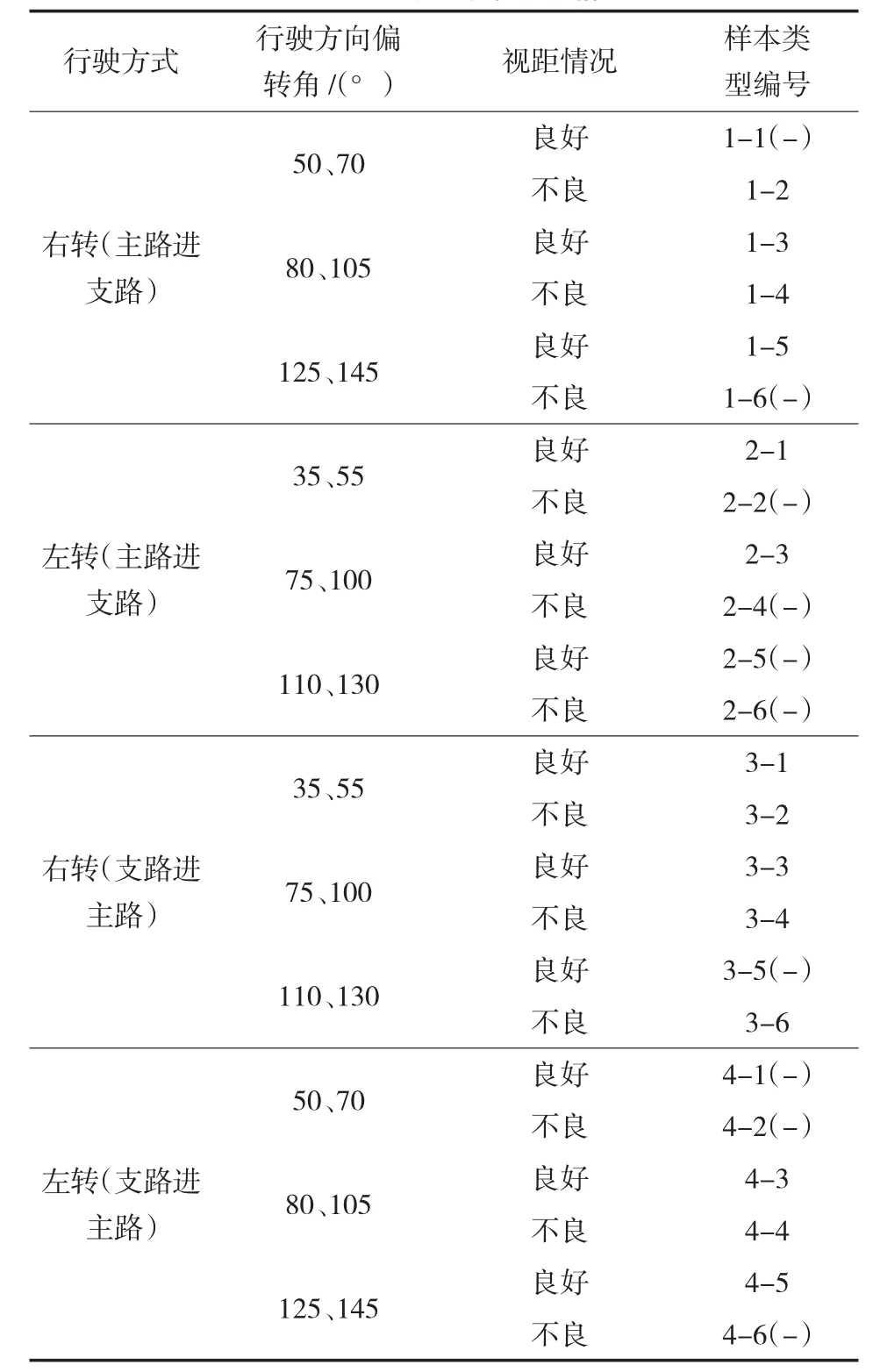
表1 数据分类及样本采集情况

2 实验结果

国内有学者在研究无信号交叉口特性时,采集离交叉口中心位置100 m、50 m断面处的速度特征［7］。在研究交叉口的区域特征时,根据不同的研究目的,将交叉口分为交叉口前、交叉口内［8］和交叉口前、交叉口内、交叉口后［9］。

本文将车辆从接近到完全通过交叉口的过程,分为驶近段和通过段(见图3),其中驶近段表示从进口道线前方100 m的位置到进口道线的区域,通过段表示从进口道线到出口道线的区域。

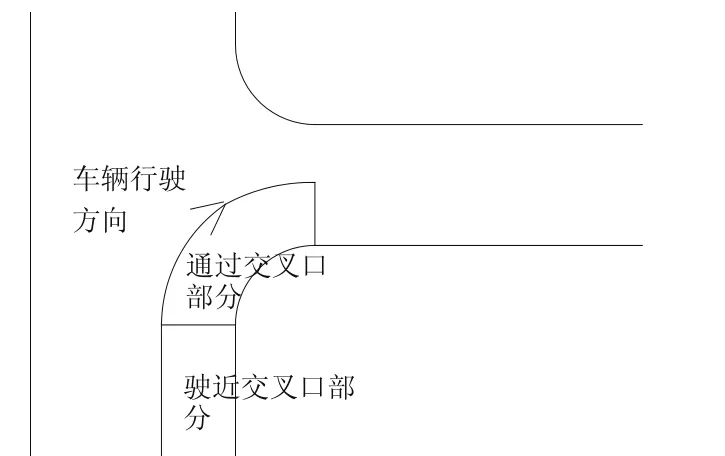
图3 驶近段与通过段区域示意图

以进口道线为到交叉口距离的零点位置,驶近段距离设为负值,通过段设为正值,记录T型右转(主路进支路)所有样本的速度分布图(见图4)。

图4 T型右转(主路进支路)速度曲线图

根据表1的所有数据类型,依次从右转(主路进支路)行驶方向偏转角50°、70°,视距良好至左转(支路进主路),行驶方向偏转角125°、145°,视距不良编号为1-1～4-6。对稳定段均速、减速位置、平均减速度、进口道处速度、加速位置、加速点速度等各特征值分别进行计算。各指标的具体计算方法见图5。

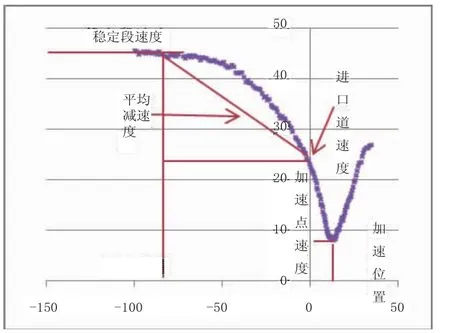
图5 特征点计算方法示意图

其中,稳定段速度表示从距离交叉口进口道100 m位置到减速位置的平均速度;减速位置表示瞬时减速度为0.3 m/s2时的位置(此时的瞬时减速度大于驾驶员松开油门时的减速度0.2～0.3 m/s2,将其作为开始减速的特征值);平均减速度是减速位置到交叉口进口道位置的平均减速度值,即平均减速度=(减速位置处的速度-进口道处速度)/减速距离;进口道位置表示交叉口进口道处的速度值;加速位置表示车辆从减速过渡到加速状态的拐点值,即车辆从减速状态到加速状态的速度最低值;加速点速度表示加速位置处的速度值。

以上各速度特征值的计算方法是基于一个样本的,现对T型右转(主路进支路)的所有样本进行各速度特征值计算,并且按表1的分类方法进行分类,然后计算各种类型的各速度特征值的均值与标准差。汇总后如表2所示。

从图5与表2可以看出,车辆在距离交叉口80 m处的速度基本在30～60 km/h之间。进口道处的车速基本在20～35 km/h之间,其中10～20 km/h占4.54%,20～30 km/h占72.73 %,30～40 km/h占22.73%。减速位置分布:距离交叉口进口道0～20 m占4.54%,20～40 m占9.09%,40～60 m占27.27%, 60～80 m占31.82%,80～100 m占27.28%。

运用相同方法,可分别得到T型左转(主路进支路)、T型右转(支路进主路)、T型左转(支路进主路)的各样本速度曲线图和汇总后的各速度特征值,见图6～图8和表3～表5。

3 速度采集方案和函数模型的确定

本节主要通过设计两种速度拟合方案,即采取3个点的速度值和采取4个点的速度值,分别用不同的函数模型来拟合进口道速度预测值。通过比较不同方案与不同函数预测模型之间的进口道预测值精度,确定合理的速度采集方案和合适的函数预测模型。

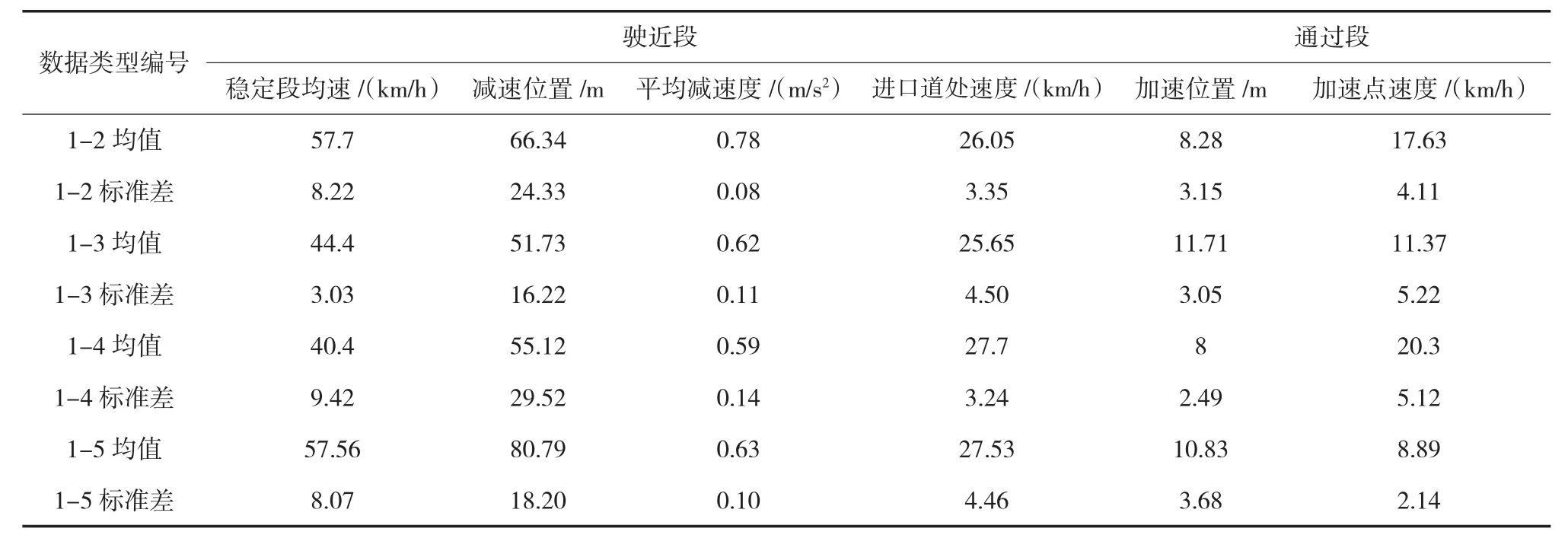
表2 T型右转(主路进支路)速度特征值

图6 T型左转(主路进支路)速度曲线图

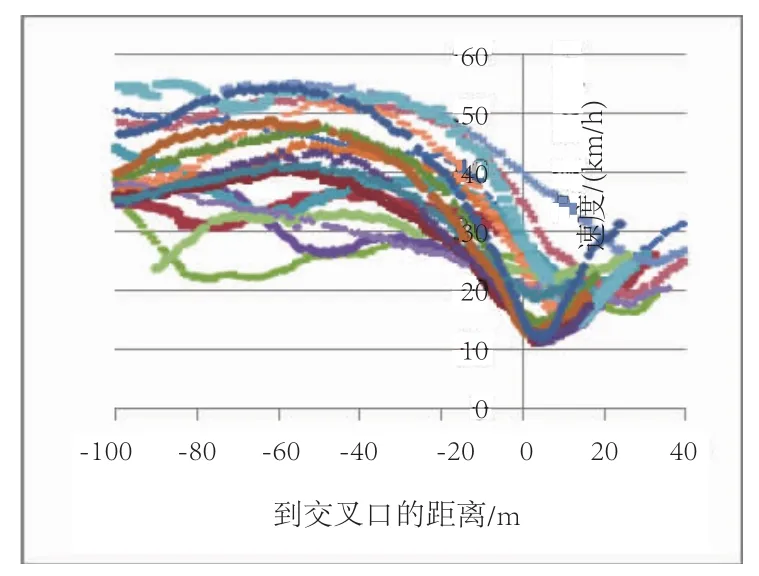
图8 T型左转(支路进主路)速度曲线图

3.1 四个点速度值采集方案

函数模型的选取主要考虑的因素有函数形式、参数个数。考虑到实际速度检测线圈的布设情况与可操作性,并且通过函数的初步拟合,现选取拟合精度比较理想的指数函数、高斯函数和二次多项式函数作为速度预测模型方案。函数形式分别如下:指数函数y=aebx+cedx,高斯函数y=ae-((x-b)/c)2,二次多项式函数 y=ae2+bx+c,三次多项式函数y=ax3+bx2+cx+d。式中涉及的参数数量为3个或4个。从上节的驶近段速度特征值表中,可以看出多数的减速位置位于距离交叉口进口道40～60 m的位置,少部分位于20～40 m和60～80 m的位置,故选取距离交叉口进口道80 m、50 m、30 m、20 m的速度值,分别记为V80、V50、V30、V20,来确定函数表达式。

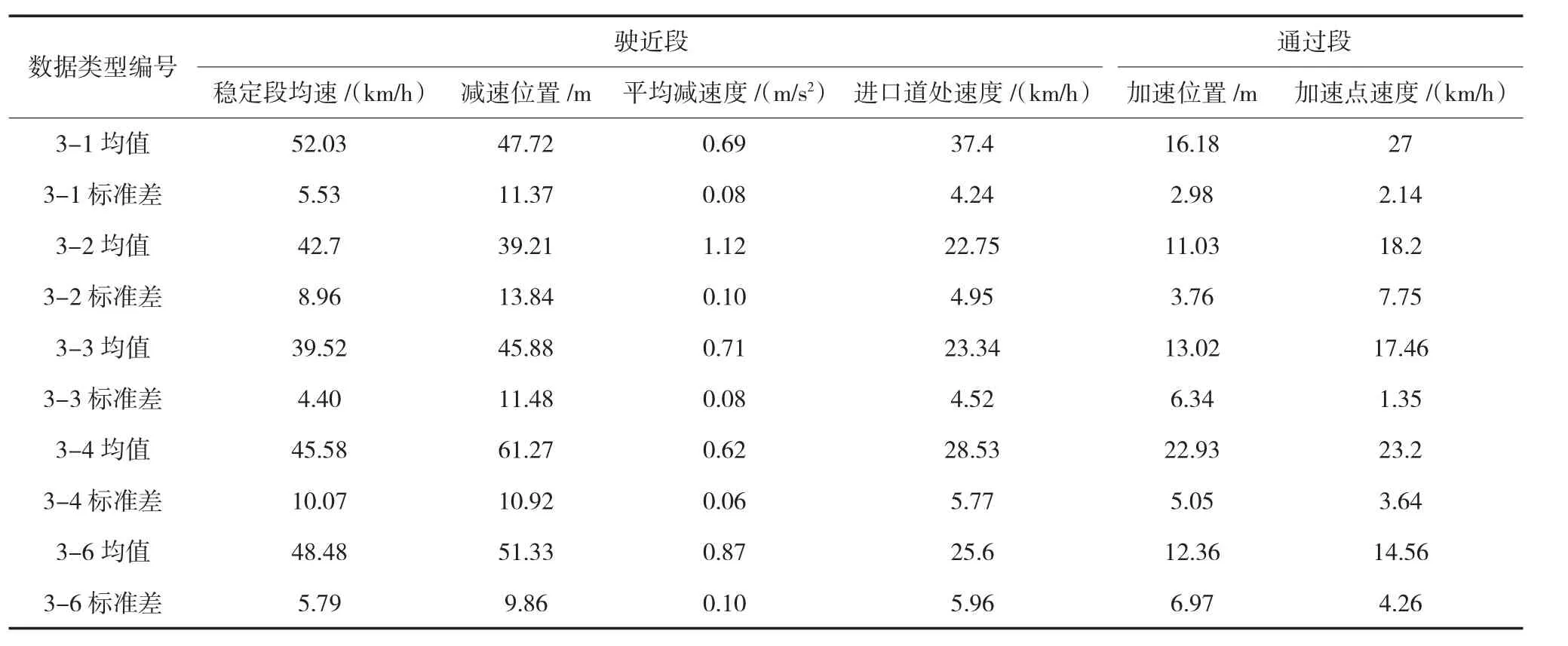
表4 T型右转(支路进主路)速度特征值

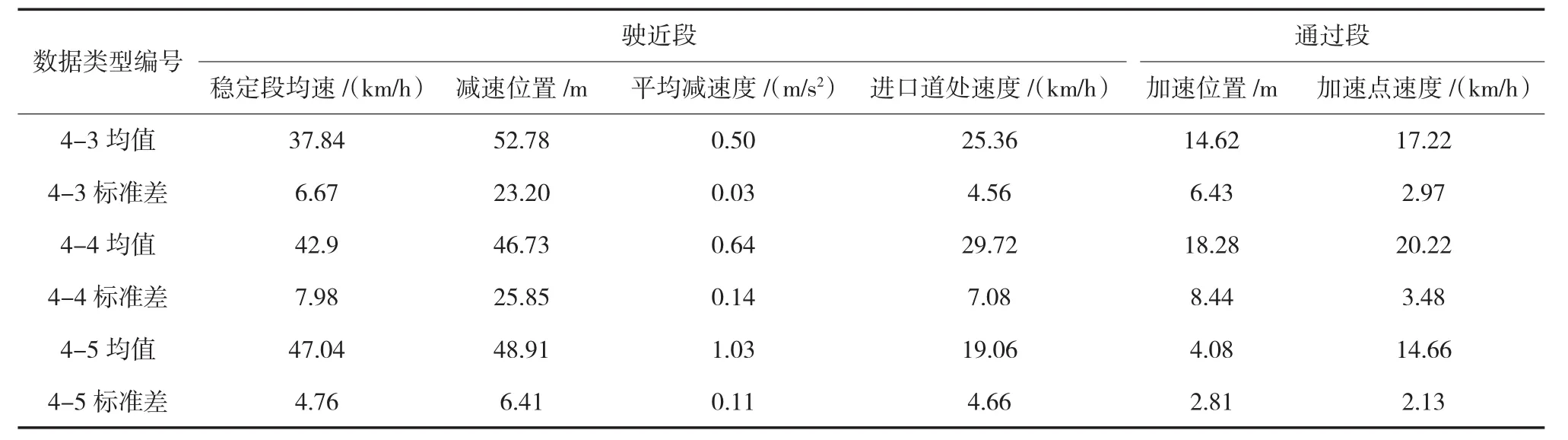
表5 T型左转(支路进主路)速度特征值

选取V80、V50、V30、V20作为函数拟合的参照点,用MATLAB确定函数表达式后便可以计算进口道位置处的速度偏差,这里为更真实反映速度预测精度,速度偏差定义为进口道处的预测值与真实值的差的绝对值。选取10个样本,计算所有样本的各拟合函数的预测偏差,进而计算各拟合函数的平均速度偏差和速度偏差的方差,见表6。

表6 函数模型拟合结果

3.2 三个点速度值采集方案

选取离进口道位置50 m、30 m、20 m作为速度样本采集点,由于指数函数和三次多项式的确定至少要有四个点样本,因此选择高斯函数和二次多项式作为三个点样本方案的函数模型。通过MATLAB函数拟合,得到表7的拟合结果。

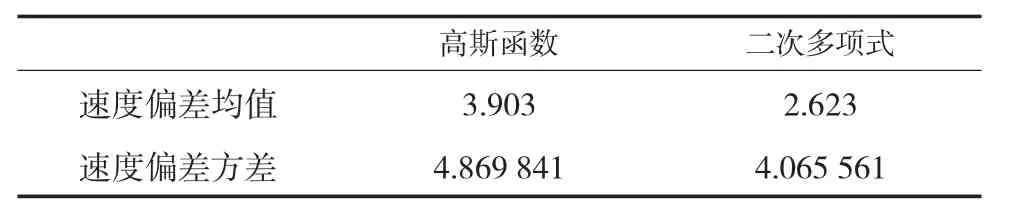
表7 函数模型拟合结果

3.3 速度采集方案与函数模型的确定

通过比较四个点速度采集方案和三个点速度采集方案,以及各拟合函数的拟合情况,可以得出三个点速度采集方案更优的结论。二次多项式的拟合结果不管速度偏差均值还是方差,三个点的采集方案都要小于四个点的采集方案。此外,从函数模型来看,对于四个点的采集方案,二次多项式函数模型具有最佳拟合效果,指数函数最不理想;对于三个点的采集方案,二次多项式函数模型较优。

4 结语

通过对车辆通过无信号T型交叉口时的速度采集,从驶近段和通过段两个角度,计算了各速度特征值,重点分析了距离进口道线80 m处车速、进口道线处车速分布以及减速位置的分布。

通过设计两种速度采集方案,用不同函数模型预测进口道速度值,得出三个点的速度采集方案并且选用二次多项式函数模型拟合时预测效果最好的结论。

［1］ 陆平,龚瑞康.道路交通事故的基本规律与对策［J］.长沙交通学院学报,1999，15(4):77-81.

［2］ 魏朗,刘浩学.汽车安全技术概论［M］.北京:人民交通出版社, 1999.

［3］ Haibo Chen， Mark Dougherty,HowardKirby. An investigation of Detector Spacingand Forecasting Performance Using Neural Networks［J］.Computer-aided civil and infrastructure engineering，2001， 16(6):422-430.

［4］ K.S.Chan， Optimal speed detector density for the network with travel time information［J］.Transportation Research Part A,2002(36): 203-223.

［5］ 储浩,杨晓光,李克平,等.基于行程时间估计的快速路检测器布设密度优化方法研究［J］.公路交通科技,2006,23(5):84-87.

［6］ 钟小明.公路三支无信号交叉口交通安全模型研究［D］.北京:北京工业大学,2006.

［7］ 钟小明,魏中华,张利,等.无信号T型交叉口交通流特性［J］.北京工业大学学报,2009，35(2):224-229.

［8］ 施晓芬.城市信号交叉口驾驶员速度控制和视觉搜索行为研究［D］.西安:长安大学,2011.

［9］ Herbert Gstalter， Wolfgang Fastenmeier. Reliability of drivers in urban intersections［J］.Accident Analysis and Prevention，2010(42): 225-234.

U491.2+3

A

1009-7716(2015)03-0142-05

2014-11-28

国家十二五科技支撑计划(2014BAG01B02)

杨轸(1974-),男,浙江上虞人,博士,副研究员,研究方向为交通安全、交通规划、驾驶仿真。