超长混凝土结构徐变作用的计算方法研究

陈顺

(上海市政工程设计研究总院(集团)有限公司，上海市 200092)

超长混凝土结构徐变作用的计算方法研究

陈顺

(上海市政工程设计研究总院(集团)有限公司，上海市 200092)

通过比较MC90、ACI、B3徐变计算模型，根据参数、图表分析和试验数据的比较结果，选择适用于我国超长混凝土结构的计算模型。并根据温度等效的原理，将徐变作用等效为温度荷载，从而给超长结构抗裂计算提供了实用的计算方法。

超长混凝土结构;徐变;抗裂;计算方法

0 前言

超长混凝土结构，即在某一方向的不设缝长度超过规范规定伸缩缝间距的混凝土结构，在建筑结构中的应用日渐广泛。在水厂工程中，对于长度超限的结构往往采用设缝的措施来减少温度作用的影响，但伸缩缝的设置不仅给设计和施工带来不便，还会影响工程的经济性。大量研究成果表明，混凝土的徐变可以在一定程度上抵消温度、收缩带来的不利影响。故在设计水厂工程的构筑物时，定量计入混凝土徐变作用可以从理论计算上得到更长的不设缝长度，减少伸缩缝数量，从而简化设计、施工过程，提高工程经济性。本文将比较各种徐变模型与试验数据的拟合程度，以此选择相对准确的计算模型，建立徐变的等效温度计算法并给出了相应的徐变等效温度表。

1 混凝土徐变

混凝土在应力作用下产生的变形，除了在龄期加载的起始应变外，还在应力的持续作用下不断增大的应变，即称为徐变。经过近百年的试验和理论研究，研究人员提出了各种徐变计算模型。现今，应用比较广泛的有美国混凝土协会提出的ACI209R-1992、欧洲混凝土委员会提出的MC90以及当代学者提出的GL2000和B3徐变收缩模型。

1.1 Z.P. Bazant的B3模型［1］

基于固结理论Z.P. Bazant等人于1996年提出了B3模型。该模型适用于的应力范围为0.4 fc’以内。此时，可以假设徐变对于应力是线性独立的，这就意味着龄期t时刻常应力下的混凝土的徐变(单位:英制):

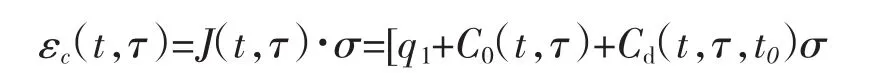
式中:q1---单位应力下的瞬时应变，q1=0.6× 106/E28;

t，τ，t0---混凝土龄期、加载时混凝土的龄期、干缩发生时混凝土的龄期;

C0(t，τ)---基本徐变;

Cd(t，τ)---附加徐变。

1.2 ACI209模型［2］

1992年美国混凝土协会ACI Committee 209提出了当前美国规范应用的混凝土徐变模型ACI Committee 209， 1992。该模型适用于标准条件下的轻质混凝土和普通混凝土。对于在τ时刻加荷，t时刻龄期的徐变函数为J(t，τ)可以表示为:

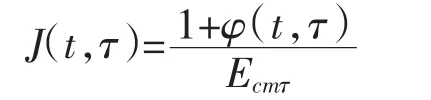
徐变系数φ(t，τ)可以表示为:

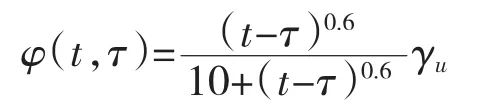
式中:γu---最终徐变系数;

Ecmτ---加荷时混凝土的弹性模量。

如果没有试验数据，最终徐变系数γu的平均值由下式给出:

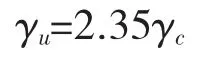
1.3 MC90(CEB/FIP)模型［3］

欧洲混凝土委员会和国际预应力联合会在1970年及1978年提出的徐变预测模型的基础上，提出了CEB/FIP(90)模型。该模型现被广泛应用于北美地区。CEB/FIP(90)模型考虑了以下影响因素:相对湿度、构件尺寸、水泥类型、水泥模量和加载龄期。对于τ时刻加载t时刻的徐变函数J(t，τ)可以表示为:

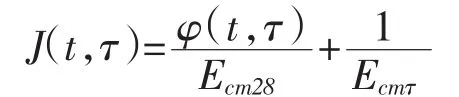
式中:Ecmτ---加荷时混凝土的弹性模量。

徐变系数φ(t，τ)可以表示为:

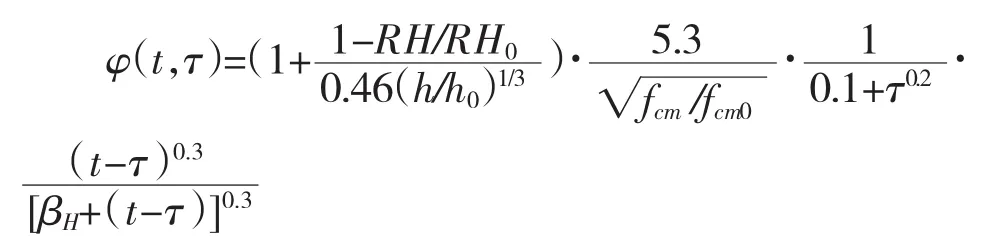
2 计算模型的图表分析

三种模型的参数各有不同，故仅比较计算龄期、加载龄期、抗压强度和相对环境湿度对徐变的影响。计算构件取1 m长的T形截面梁，如图1所示。

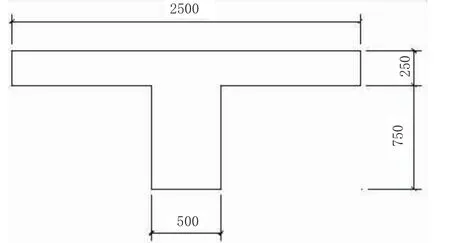
图1 计算构件截面图

2.1 计算龄期t

在研究徐变与计算龄期的关系时，以τ=16，fcm=40 MPa，h=50%，作为固定参数。对比混凝土加载持荷30 d、100 d、1 000 d和5 000 d内单位应力下的应变(见图2～图5)。

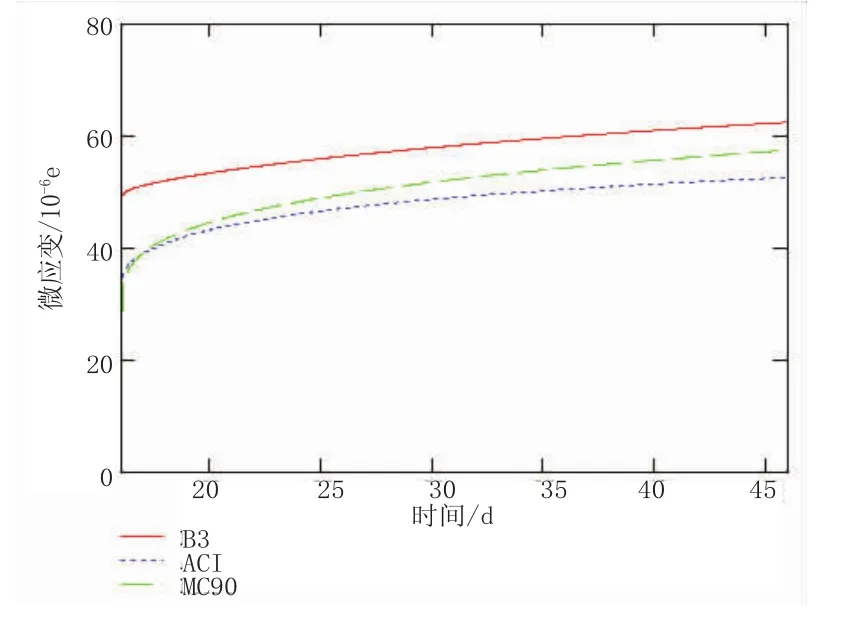
图2 持荷30 d的应变曲线图

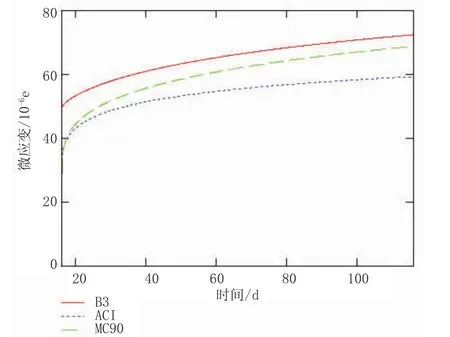
图3 持荷100 d的应变曲线图

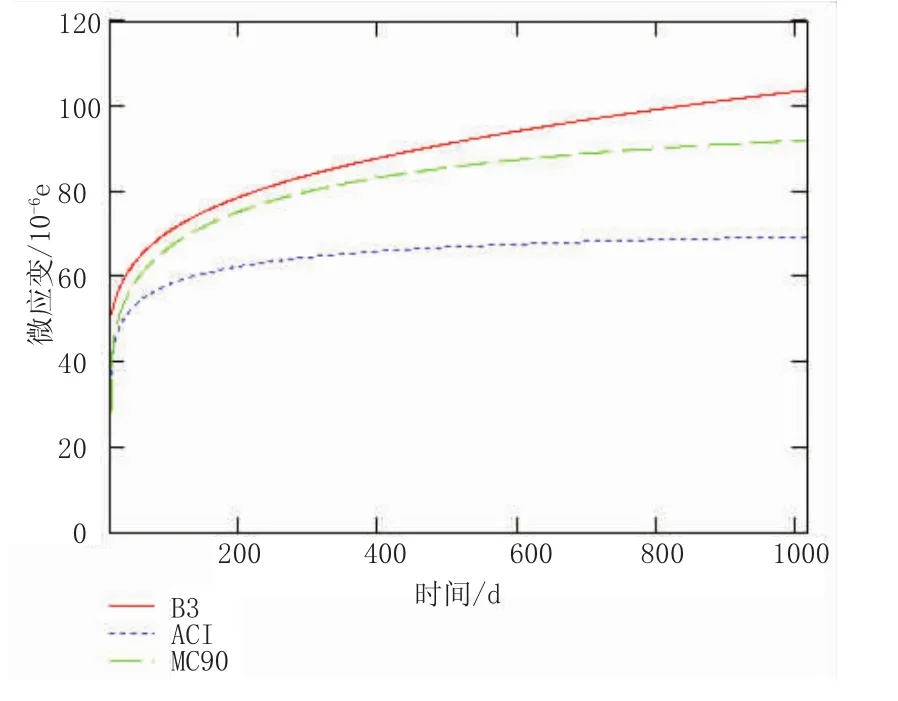
图4 持荷1 000 d的应变曲线图

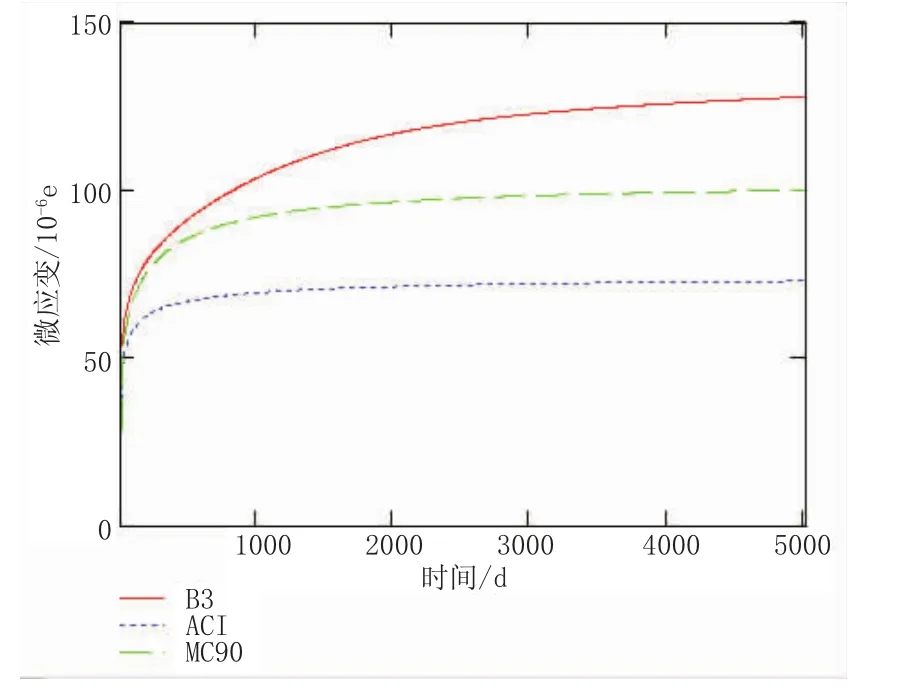
图5 持荷5 000 d的应变曲线图

图2是持荷30 d各模型的计算结果。早龄期时，B3模型比ACI和MC90的计算结果大。ACI和MC90模型的早期结果比较接近，但是随后MC90曲线渐渐向B3靠拢。前10 d内，B3曲线比较平缓，ACI和MC90曲线的增长较快。

图3是持荷100 d的计算结果。随着时间的增长，B3和MC90曲线越来越接近。浇筑第八十天以后，两曲线的斜率越来越接近，增长速度相仿。ACI的增长速度相对比较慢。

在图4中，达到持荷400 d以后，也就是一年零一个月的时候，MC90曲线的增长趋势已经慢慢降低，而B3曲线的增长趋势仍比较快。ACI曲线仍然比较平缓，与B3和MC90的结果相差越来越多，其计算值明显比较小。

在图5中，持荷3 000 d，也就是持荷第八年时，B3曲线已经开始趋于平缓，徐变增加的趋势很小。另两条曲线在第2 000 d左右开始不在增长。从持荷5 000 d的结果来看，B3模型的计算值明显大于另两个模型。表1给出了三种计算模型在不同持荷时间下的应变。

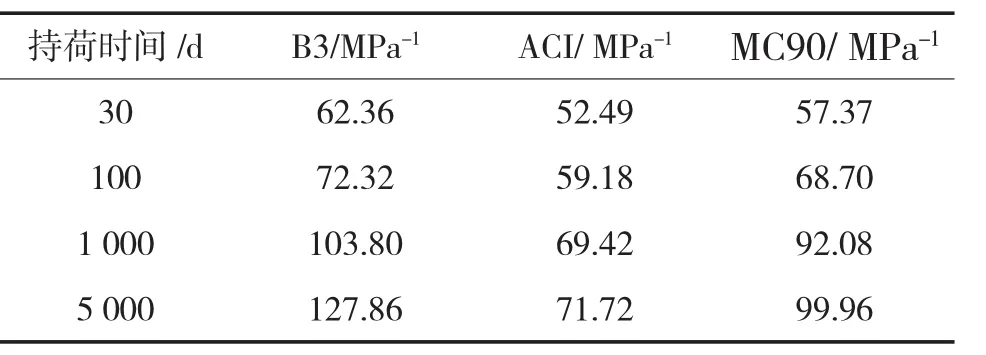
表1 不同持荷时间下的应变一览表

2.2 加载龄期τ

在研究徐变与加载龄期的关系时，以τ=16，fcm=40 MPa，h=50%，作为固定参数。对比分析混凝土加载龄期为100 d和1 000 d内单位应力下的应变(见图6、图7)。

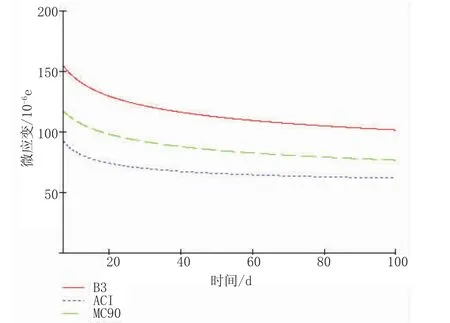
图6 100 d内加载的应变曲线图

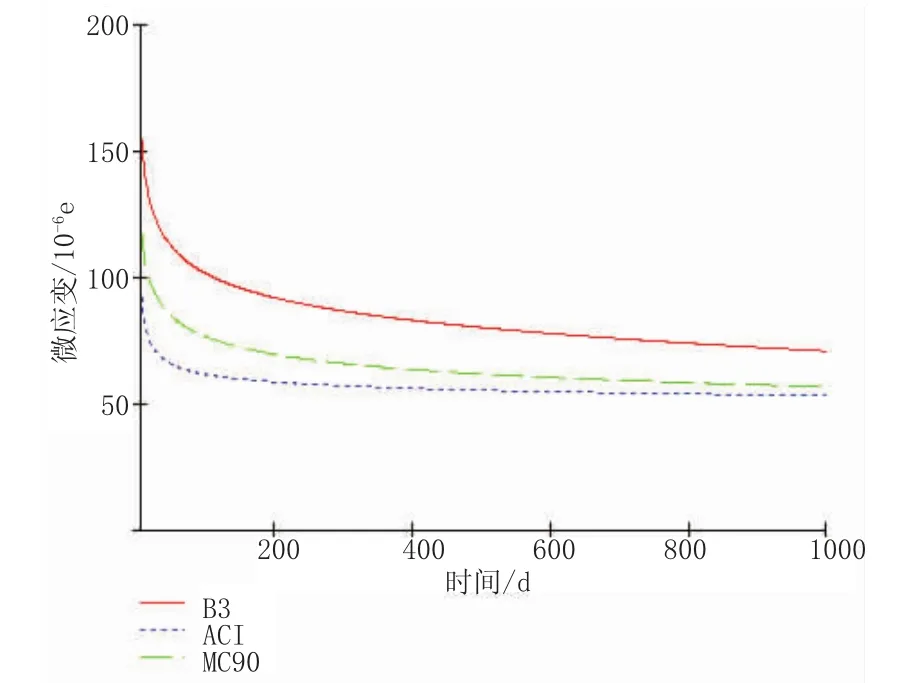
图7 1 000 d内加载的应变曲线图

从图6的曲线来看，三种计算模型都表现出了早加载徐变大的特征。随着加载龄期的增长，其对徐变的影响也随之降低。

由图7可以看出，加载越晚，徐变越小。B3曲线要高于另两条曲线。200 d后，对ACI曲线曲率的影响不大。400 d后，MC90曲线的下降幅度也很有限。MC90曲线渐渐接近ACI曲线。随着τ的增长，B3曲线的降幅比另两条大。B3曲线变化幅度较大，说明B3模型对于加载龄期比较敏感。因在计算时需要准确地选择加载龄期的时间。表2给出了t=10 000时，各龄期加载的应变计算值。

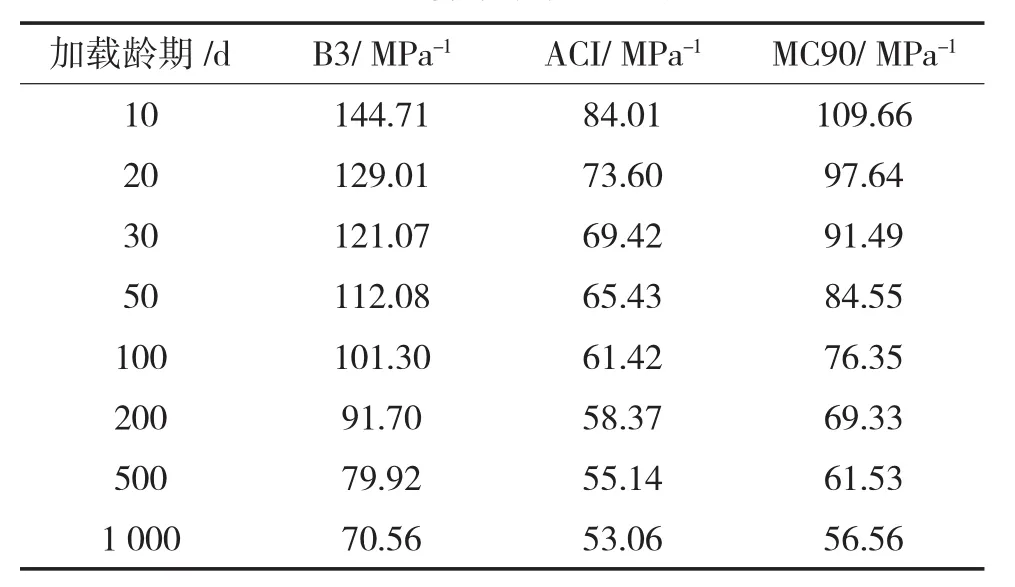
表2 不同加载龄期的应变一览表

由表2可以发现，30 d龄期加载和10 d龄期加载所产生的徐变相差20 MPa-1左右，接近总应变的20%。因此，在实际工程中，加载龄期越晚越好。

2.3 抗压强度fcm

在研究徐变与混凝土抗压强度fcm的关系时，以t=10 000，τ=16，h=50%作为固定参数。fcm的变化范围取B3模型与MC90模型的交集，即20～70 MPa。

如图8所示，随着抗压强度的升高，混凝土的徐变逐渐减少。B3和MC90曲线在低强度段结果比较接近。ACI和MC90曲线在高强度段逐渐接近。在整个强度范围内MC90曲线的变化幅度较大。说明MC90模型对强度比较敏感。B3和ACI曲线的变化趋势一直比较平缓，受强度的影响小。

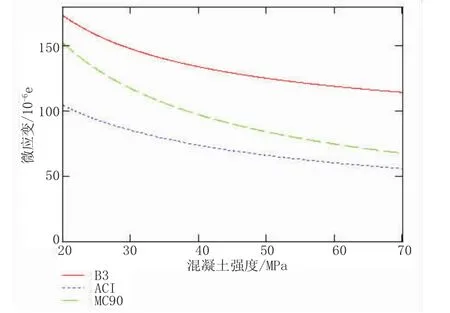
图8 抗压强度与徐变的关系曲线图

2.4 相对环境湿度h

在研究徐变与混凝土抗压强度fcm的关系时，以t=10 000，τ=16，fcm=40 MPa，作为固定参数。不同相对湿度下的应变计算值如表3所列。

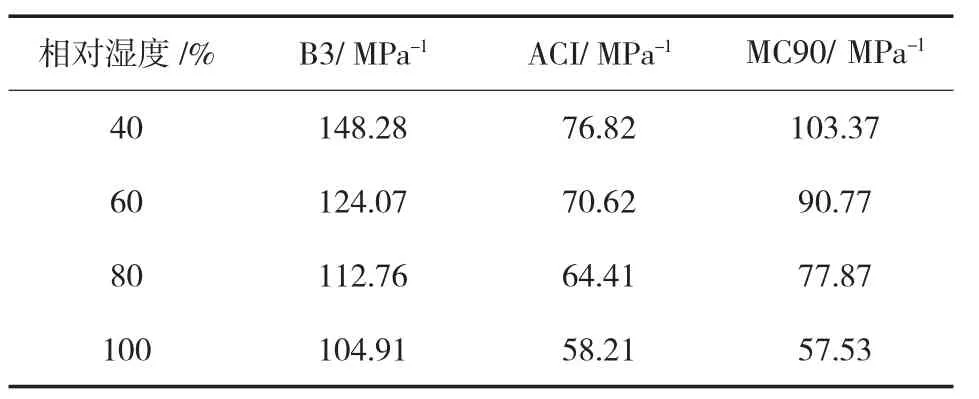
表3 不同相对湿度下的应变一览表

图9为相对湿度与徐变的关系曲线图。在图9中，B3的值较高，在相对湿度50%～70%区段内下降速度比较快。当相对湿度大于70%以后变得平缓。ACI曲线的变化比较一直，其值明显偏小。MC90曲线对相对湿度比较敏感，变化幅度大。

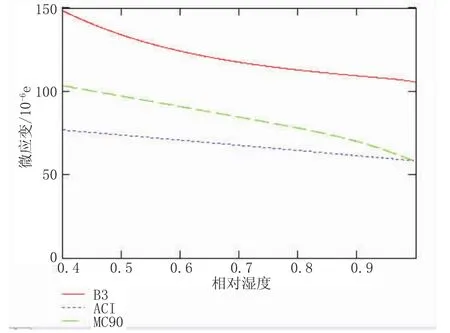
图9 相对湿度与徐变的关系曲线图

3 计算模型与试验数据的比较

徐变是一个作用周期相当长的过程。因此，将三个模型的计算结果与Russell & Larson(1989)［4］的365～5 000 d试验结果进行比较，得到如表4所列的结果。

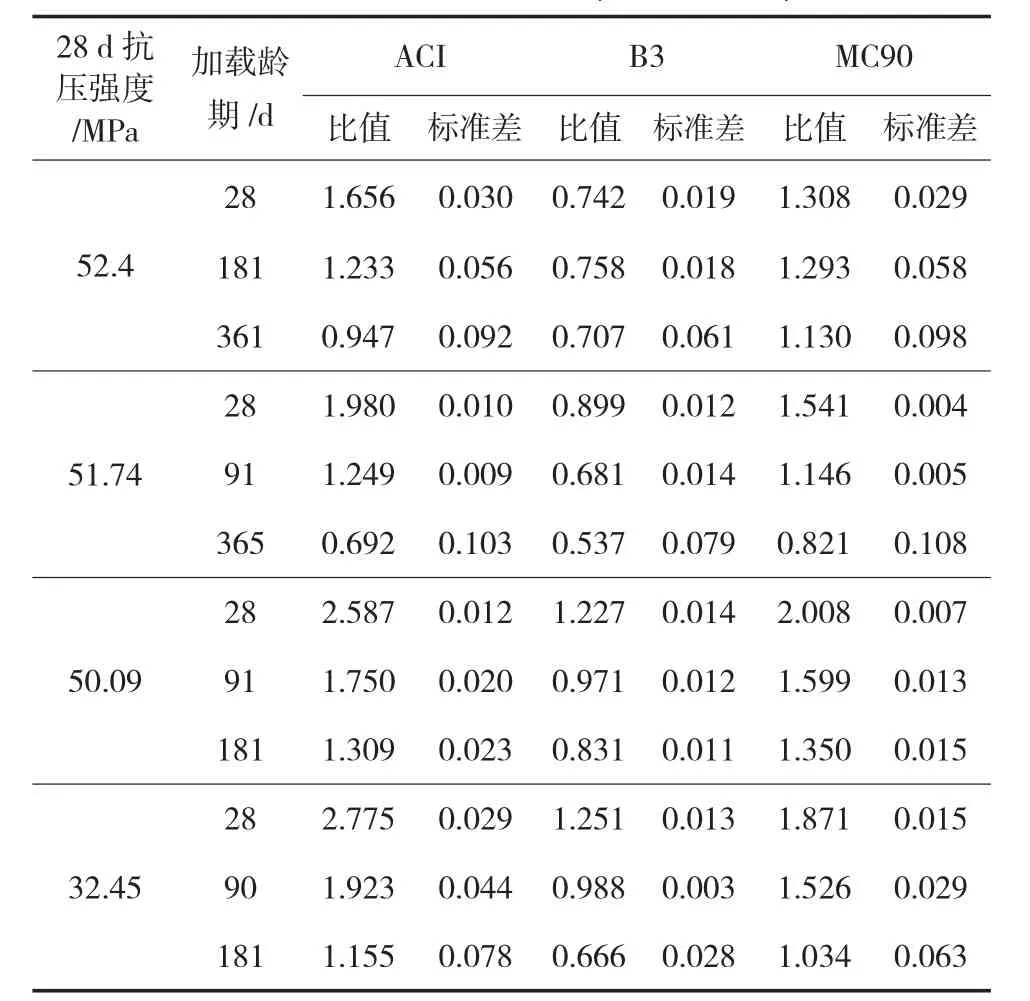
表4 计算值与试验值的比较(365～5000 d)一览表

4 计算模型的选择

比较计算与试验数据时，通过试验值与计算值的比值来判别模型的符合程度;通过标准差来判断离散程度。从比较结果来看，ACI209和MC90的结果都比试验数据小，B3的稍大。强度大于51.74 MPa的区间内，MC90的符合程度比较好;小于50.09 MPa的区间内，B3的符合程度最好。加载龄期超过181 d时，ACI209和MC90的符合程度都比较好。但是在28 d加载时，B3的符合程度远远好于另两个模型。另外，综合地看B3模型的标准差也是最小的。现今国内大部分工程常用的混凝土标号一般不超过C50，而且许多工程在混凝土浇筑后很快就要承担施工荷载。因此，B3模型是比较符合我国工程实际情况的。

5 徐变作用的等效温度计算法

徐变作用变形的方向是与受力方向一致的。因此，对于受拉和受压构件，徐变作用的效果是不同的。本节主要讨论常应力下受压和受拉构件徐变作用的等效。

5.1 受拉构件

受拉徐变产生的效果可见图10所示。在图10中，图(1)表示自由状态下的混凝土构件;图(2)表示在施加了一个拉力弹簧约束的瞬间，构件中产生的全部都是弹性拉应变;图(3)表示过了一段时间以后，由于徐变的作用，构件变形进一步增加。此时弹簧力由于构件的变形而减小，构件内部的应力随之降低。故对于一个部分约束混凝土构件来说，在徐变作用下，构件的应力会降低，而应变会增加。对于受拉构件来说，图10(2)到图10(3)的过程类似升温的过程。故将徐变产生的应变等效为相应的升温荷载是合理的。

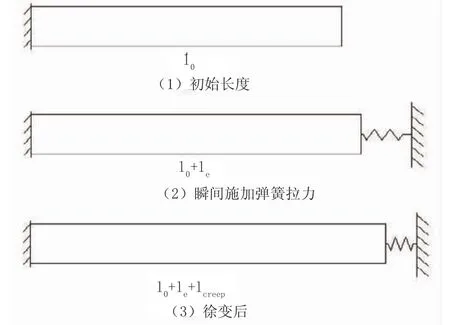
图10 受拉构件的长度变化示意图

将此方法用于B3模型后得到单位应力下徐变的等效温度荷载:

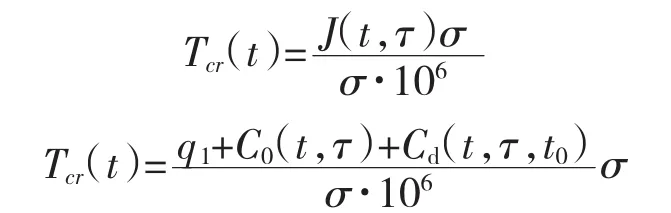
式中:σ---徐变方向上的拉应力，MPa。

5.2 受压构件

采用与受拉相同的方法分析受压构件，可发现受压徐变与降温类似。将受压徐变等效为降温荷载时，可以得到以下公式:

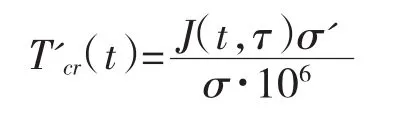
6 徐变等效温度计算法的工程应用

徐变是随着应力、时间不断变化的非线性过程。计算过程非常复杂，难以在工程设计中使用。实际上，工程设计时往往不计入徐变作用。为了方便广大设计人员进行徐变计算，本文计算了一般条件下，不同混凝土在不同应力下各阶段的徐变等效温度表(见表5、表6)。

从表5及表6中各阶段龄期内应力对应的等效温度可以得到整个计算龄期内徐变对结构的影响。

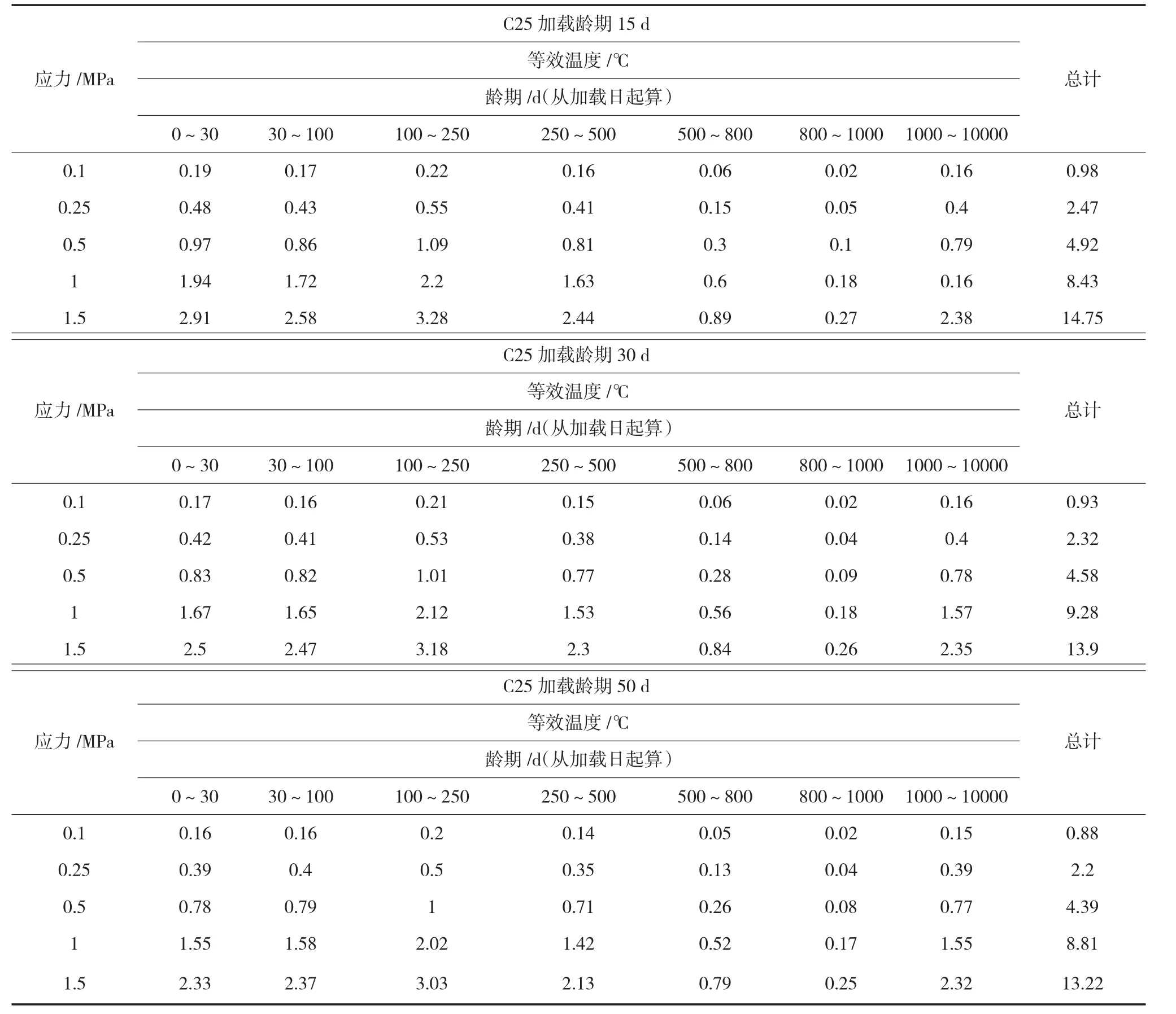
表5 C25混凝土不同应力下徐变等效温度(0～10000 d)一览表

7 总结

长久以来，混凝土徐变作用的计算始终难以应用到实际的设计过程中。徐变等效温度计算法及其等效温度表的提出，方便了广大设计人员进行徐变的定量计算。同时，也为进一步挖掘工程结构最大不设缝长度的潜力，提供了一条新的路径。

［1］ Z. P. Bazant， Sandeep Baweja.Justification and refinements of model B3 for concrete creep and shrinkage 1. Updating and theoretical basis.Materials and Structures， 1995， 28， 415-430.

［2］ ACI Committee 209. (1992).Prediction of creep， shrinkage and temperature effects in concrete structures(209R-92)［M］.American Concrete Institute.

［3］ CEB-FIP Model Code for Concrete Structures. (1990).

［4］ Russell， H.G. and Larson， S.C.， 1989.Thirteen Years of Deformations in Water Tower Place.ACI Structural Journal，Vol. 86(2)， pp.182-191.

TU311.4

A

1009-7716(2015)04-0161-06

2014-12-12

陈顺(1982-)，男，浙江宁波人，硕士研究生，工程师，从事给水排水工程结构设计工作。

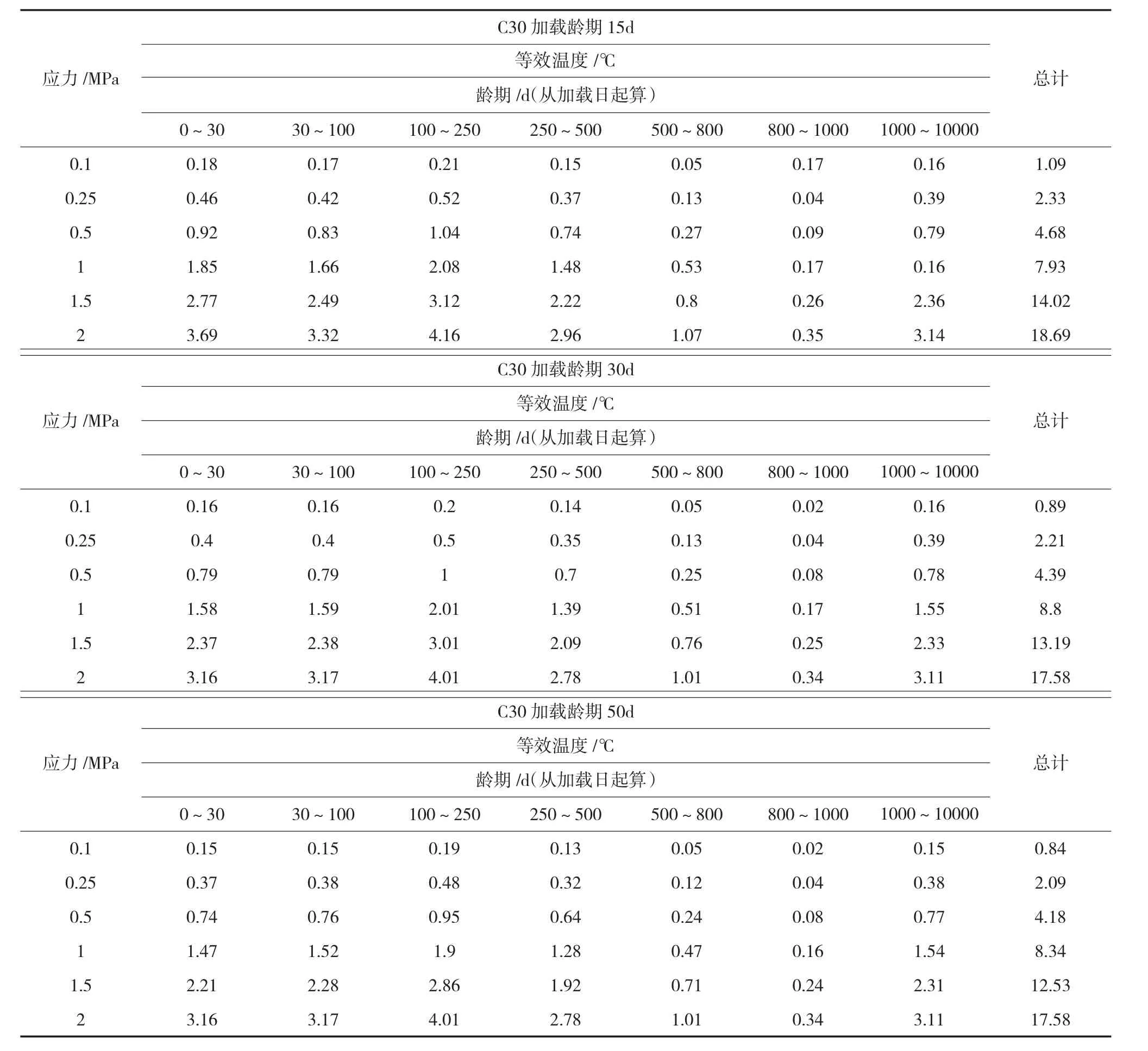
表6 C30混凝土不同应力下徐变等效温度(0～10000 d)一览表