基于SIFT特征与预测的运动目标检测算法
2015-10-22吴忠良余升
吴忠良 余升


摘 要: 为了在动态场景下对运动目标进行快速检测,提出一个改进的SIFT特征匹配的检测算法。首先采用SIFT方法提取匹配的特征点;然后为全局运动建立起旋转参数模型,并使用RANSAC方法排除外点的影响,运用最小二乘法求解全局运动参数;最后利用基于残差图像块的更新策略对特征点进行更新。该算法是基于预测的SIFT特征点匹配算法,不仅保持了SIFT方法的优越性能,而且提高了检测目标的速度。与块匹配算法的实验结果对比表明,该算法可以实时准确地检测出运动目标。
关键词: 目标检测; SIFT特征; 旋转参数模型; 动态场景
中图分类号: TN911.73?34; TP391 文献标识码: A 文章编号: 1004?373X(2015)19?0087?04
Abstract: An improved detection algorithm of SIFT feature marching is provided for rapid detection to moving object in dynamic scene. The matched feature points are extracted by SIFT method, and the rotation parameter model is established for global motion. The influence of exterior points is eliminated by RANSAC method. The global motion parameters are solved by the least square method, and the feature points are updated by the updating strategy based on residual image block. This matching algorithm is based on the predicted SIFT feature points, which can remain the high performance of SIFT method and improve the detection rate of the object. Compared with the experimental results of block matching algorithm, it demonstrates that this algorithm can detect moving object accurately and in real?time.
Keywords: object detection; SIFT feature; rotation parameter model; dynamic scene
0 引 言
现代监控系统中,需要对运动目标进行实时快速的检测,传统的固定摄像机由于其监控范围有限,逐渐被可旋转的摄像机代替。动态场景下的图像不断变化,信息处理相对静态场景更加复杂,因此动态场景下目标检测的研究具有重要的意义。目前检测运动目标的方法主要有:时间差分法[1]、光流法[2]、背景减除法[3]、匹配的方法[4]等。时间差分法对环境有着较强的适应性,但由于不能对检测的所有特征进行提取,无法全部的对目标区域进行检测;光流法适用范围较广,但该算法较为复杂,运算量很大,不适合实时的检测动态场景下的运动目标;背景减除法可提供完整的目标特征,但该方法容易产生离散噪声点,并且容易受到光照和灰度等级变化的干扰,需要建立背景模型对背景图像进行实时更新;特征点匹配的方法,在相邻帧中分别提取特征点,并匹配特征点,再利用匹配的特征点对求解全局运动参数。由于特征点匹配的方法适合摄像机随意转动的情况,而且只需要对某些有特征的、稳定的点进行计算,大大提高了算法速度。所以本文采用特征点匹配的方法。
SIFT特征点由David Lowe于1999年首次提出[5?6],此方法对检测目标的旋转、尺度缩放、视角变化及亮度变化具有良好的不变性,并对遮挡和噪声也有很好的鲁棒性。匹配点多而且稳定也是该算子的一个重要特点。由于SIFT在用于摄像机运动参数求解时运算量较大,难以达到实时性的要求,因此,本文针对实时性检测的需要,在SIFT算法的基础上加以改进,提出了基于预测的SIFT特征点匹配算法,可以实时快速地检测出运动目标。
1 SIFT特征点
SIFT算法是一种提取局部特征的算法,该算法的主要思想就是在图像中提取出特征点,使图像的匹配转化为特征点向量的相似性度量。SIFT 特征匹配算法主要有三个步骤:SIFT特征点的检测;SIFT特征描述符的生成;SIFT 特征向量的匹配。算法过程如图1所示。
SIFT算法通过比较图像灰度值得到特征向量,特征提取是SIFT算法的重点。特征的提取包括初步定位特征点,精确定位特征点,为每个特征点明确方向和生成关键点描述算子。一般提取越多的图像特征,越能反映出图像中目标的真实特征,匹配的结果也会更加精确,但会增加算法的复杂性和运算时间。为了达到实时性的效果,特征的提取并非越多越好,SIFT算法只需要很少的必要的特征匹配点,就可以很好地对特征进行匹配。
2 快速检测匹配算法
2.1 求解全局运动参数
对运动目标的检测需要消除摄像机的移动影响。摄像机的主要运动方式有平移、旋转、缩放和俯仰,需要运用合适的全局运动模型及运动参数,运用比较广泛的有仿射参数模型和旋转参数模型[7?8]。仿射参数模型相对简单,适合摄像机旋转运动较小时的情况;旋转参数在摄像机旋转角度较大时可以更好地描述摄像机的运动,因此采用8参数旋转模型[9],满足摄像机的各种运动情况。endprint
式中:参数[A]为旋转参数矩阵,主要由摄像机的旋转和平移参数决定,同坐标参数无关。实际中无法得知摄像机的旋转角度和平移量,需要通过其他方法求解矩阵[A。]
使用特征点匹配全局运动参数的思想是:在相邻两帧中分别搜索特征点,再对特征点对匹配,得到[F=f1, f2,…, fn,…, fN,]表示匹配点对的集合,其中[fn=(Xt-1,n,Xt,n)]为第[n]对匹配点,并用最小二乘法求最优解。
运用特征点进行运动补偿时,匹配的结果可能是失真的,即发生误匹配。失真的点又称作外点。相对来说,产生外点的概率较小,但为了避免引入外点造成全局运动的估计发生较大偏差,需要采取方法将外点从数据点中去除。因此采用RANSAC[10?11](随机抽样一致)的方法去除误匹配点,使用该方法后再利用最小二乘法[12]便可求解出较为准确的参数矩阵。
2.2 基于预测的特征点匹配算法
摄像机拍摄所得的图像序列中,每两个帧之间的间隔时间很短,帧之间的变化很小,相差一般只有几个像素。由于当前帧包涵了下一帧的大量信息,据此提出基于预测的快速匹配方法,即根据当前帧的特征点对下一帧的特征点进行预测。该算法根据预测的特征点的位置,小范围的搜索特征点,得到当前帧的特征点。具体步骤如下:
(1) 设第[t-1]帧图像的特征点集为[Pt-1={pt-1,1,pt-1,2,…,pt-1,m}];
(2) 根据特征点[pt-1,m]和运动参数,预测[t]帧的特征点[pt,m;]
(3) 以特征点[pt,m]为圆心,在半径为[N]个像素的圆内搜索特征点[pt,n]。将[pt,n]与[pt-1,m]进行匹配,若匹配成功,则建立匹配点对[ft,n=(pt-1,m,pt,n),]即可得到匹配点对的集合[Ft={ft,1, ft,2,…, ft,n,…, ft,N}]以及第[t]帧的特征点集[Pt={pt,1,pt,2,…,pt,n,…,pt,N}]。
这种预测下一帧的方法使匹配在限制的范围内进行,缩小了搜索的范围,减少了误匹配的发生。其中[N]值的大小直接关系到运算量的大小,通过在多组动态场景下拍摄视频的实验,确定[N=3]时效果最佳。
2.3 基于残差块的特征点更新
在动态场景下,摄像机拍摄的视角会不断变化,图像的特征也随之变动,故此需要对特征点进行及时更新。可以设一个最低匹配值[Tf],当特征点的匹配数低于[Tf]时就立刻更新。[Tf]设置较大会造成运算量过大,影响算法效率;设置较小会使平均匹配点数降低,造成最小二乘解不准确。根据多组试验选取最佳[Tf=15]。
特征点的更新需要对图上的点进行搜索,由于特征点主要集中在检测目标中且在求解运动参数时,真正起作用的是背景点,所以需要将包括检测目标即前景的一块区域排除。
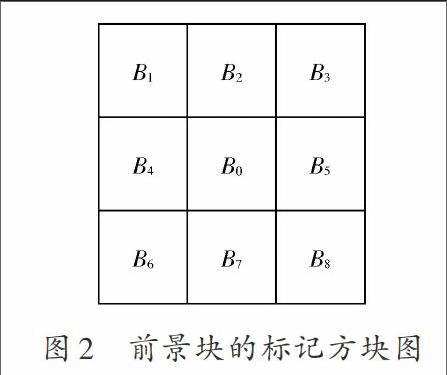
如图2所示,采用基于残差图像的方法将前景区域进行快速标记。将残差图像分成[m×n]个大小的块,计算每个块的SAD[13],并按大小进行排序。[SAD=i=0Mj=0Nψi,j,]其中[ψi,j]是[(i,j)]的残差。图2中,[B0]是当前预选前景块,若邻域8个图像块的SAD值有超过一半排在总SAD值的前30%,则将当前预选前景块标记为前景块,将每个预选前景块都依次进行排查。块参数[m]和[n]的取值决定了计算量的大小和前景块标记的准确性,通过实验确定设为[16×16]最为合适。
2.4 算法实现的具体步骤
若已知[pt-1,1]为第[t-1]帧的特征点集,[At-1]为第[t-1]帧的仿射参数矩阵。对第[t]帧运动目标进行检测,其算法详细步骤如下:
(1) 根据2.1节提出的方法搜索出第[t]帧所有特征点[pt,n]并保存在特征点集[Pt]中,并用[Pt-1]和[Pt]进行匹配并建立匹配点对[Ft]。
(2) 用RANSAC去除[Ft]中可能存在的误匹配点,再用最小二乘法求解出[t]帧的仿射参数矩阵[At]。
(3) 利用式(2)对[t-1]帧图像[It-1]中摄像机旋转导致的运动进行补偿,得到补偿图像[It]。再将补偿图像[It]和第[t+1]帧图像[It]做背景差处理,得到残差图像[Iobj]。
(4) 判断得到的[Pt]点集中的特征点数目是否小于[Nf],若小于则用2.3节中的方法进行更新。
(5) 将得到的[Iobj,][At,][Pt]进行保存,并同时进行背景的实时更新。
3 实验结果与分析
为了验证算法的效果,将本文算法同块匹配算法进行实验对比。使用Visual Studio 2010在Intel i3 CPU内存4 GB的PC机的实验平台上进行调试。通过视频实验对结果进行比较和分析。具体的实验结果如图3和图4所示。
图3为分辨率为[320×240]的实拍图像序列。图3(a)为原图像序列的第30帧和70帧,图3(b)为块匹配算法得到的实验结果,图3(c)为本文算法的实验结果。通过对比可以看出,匹配算法检测出的目标图像较为模糊,轮廓有残缺,背景中有东西没被除去。本文算法检测的目标图像十分饱满和清晰,完全排除了背景中的干扰。此实验结果说明,本文算法继承了SIFT算法的优越性,在摄像机快速旋转时可以有效检测运动目标。
图4是对分辨率为[352×288]的标准序列的测试结果。从实验结果可以看出,两种算法都能检测出目标。匹配算法检测出的目标比较模糊,背景中的观众并没有完全去除。由于摄像机的运动不仅仅是平移,匹配算法不能良好适应。本文算法测得的结果明显较为清晰。通过此实验可以说明,本文算法对摄像机在复杂的运动下检测运动目标同样适用。
表1是两种算法的运行时间比较,可以看出本文算法耗时要小于块匹配法,运行效率有了很大提高,说明本文算法十分适合实时检测目标。该算法采用旋转模型得到全局运动参数,并使用基于预测的方法可以测出比较清晰的运动目标,说明本文提出的算法具有很强的实用性。endprint
4 结 论
本文提出了一种基于预测的匹配算法,针对动态场景下的目标进行检测。首先利用SIFT 算法提取出特征点,再构建全局运动模型来描述摄像机的运动,通过运用最小二乘法求解运动参数,其中采用RANSAC方法去除外点;最后基于残差图像块的特征点更新策略保证求解参数的准确性。实验结果证明,该算法可以准确实时地检测出移动摄像机下的运动目标。
参考文献
[1] 周若谷.基于高斯背景建模和时间差分法的目标检测研究[J].电脑编程技巧与维护,2014(4):28?29.
[2] 张瑜慧,沈洋.基于图像融合的运动前景检测方法[J].现代电子技术,2013,36(24):67?69.
[3] 张咏,李太君,李枚芳.利用改进的背景差法进行运动目标检测[J].现代电子技术,2012,35(8):74?77.
[4] BOROS E, ROSCA G, IFTENE A. Using SIFT method for global topological localization for indoor environments [C]// Proceedings of 2010 the 10th IEEE Workshop of the Cross?Language Evaluation Forum. Corfu: IEEE, 2010: 277?282.
[5] LUO J, OUBONG G. A comparison of SIFT, PCA?SIFT and SURF [J]. International Journal of Image Processing, 2009, 3(4): 143?152.
[6] 傅卫平,秦川,刘佳,等.基于SIFT算法的图像目标匹配与定位[J].仪器仪表学报,2011,32(1):163?169.
[7] 赵亚湘,樊晓平,刘少强.基于运动矢量场的运动目标区域检测[J].光电子·激光,2014,25(12):2387?2392.
[8] SU Y P, SUN M T, HSU V. Global motion estimation from coarsely sampled motion vector field and the applications [J]. IEEE Transactions on Circuits and Systems for Video Technology, 2005, 15(2): 232?242.
[9] LOWE D G. Distinctive image features from scale?invariant keypoints [J]. International Journal of Computer Vision, 2004, 60(2): 91?110.
[10] 郭红玉,王鉴.一种基于RANSAC基本矩阵估计的图像匹配方法[J].红外,2008,29(2):5?8.
[11] 曲天伟,安波,陈桂兰.改进的RANSAC算法在图像配准中的应用[J].计算机应用,2010,30(7):1849?1851.
[12] 鲁铁定,陶本藻,周世健.基于整体最小二乘法的线性回归建模和解法[J].武汉大学学报:信息科学版,2008,33(5):504?507.
[13] HE Y W, FENG B, YANG S Q, et al. Fast global motion estimation for global motion compensation coding [C]// 2001 IEEE International Symposium on Circuits and systems. Sydney: IEEE, 2001, 2: 233?236.endprint
