土方量实际算量中应用方法分析比较

林冬冬　丛佳男

摘要：土方量计算方法主要有断面法、等高线法、方格网法、DTM法及平均高程法，不同方法计算同一场地土方量相差较大，这直接关系到项目的合理性及成本预算，本文通过实例对比分析DTM法、方格网法及平均高程法三种方法的差异，并结合实际施工情况优化改进，得出基于三角网规则的方格网法、DTM法及平均值法能够最快最准确计算出土方量，为施工单位计算土方量提供了一定的帮助。

关键词：土方量；DTM法；方格网法；平均值法

在各种工程建设如铁路、公路、港口、城市规划等中，土方量计算是一项经常性的、不可缺少的工作，且在整个工程量中，土方工程常占有较大比例。土方量大小及计算精度的高低直接关系到项目的合理性和投资预算，因此快速准确地计算土方量对开展规划设计、控制总投资及分配资金具有重要意义。为此，本文对工程土方量计算方法中的断面法、等高线法、方格网法、基于数字高程模型（DTM）法及平均高程法的基本原理、方法進行比较分析，并考虑实际应用中的条件限制，进而探索出适合工程实际应用的土方量计算方法。

1土方量计算原理及方法

1.1断面法

在地形变化较大、场地狭窄的带状地区，可以用断面法计算土方量。在地形图上或碎部测量的平面图上，根据土方计算的范围，以一定的间距等分场地，将场地划分为若干个相互平行的横截面；按照设计高程与地面线所组成的断面图，计算每条断面线所围成的面积；以相邻两断面面积的平均值乘以等分的间距，得出每相邻两断面的体积；将各相邻断面的体积累计加和求出总体积，这种方法称为断面法（图1）。

图1土方断面示意图

根据两相邻的设计断面填挖面积的平均值乘以两段面的距离，就得到两相邻横断面之间的挖、填土方工程量。公式如下：

——土方工程量；

， ——相邻两断面的挖方或填方面积；

——相邻两横断面之间的距离。

在计算过程中，距离 一般根据需要选取，面积 ， 则需要根据横断面测量资料采用下面两种方法计算：

（1）几何图形法。根据实地测量有关的边、角元素进行面积计算，将不规则的图形分割成简单的矩形、梯形或三角形等简单的几何图形分别计算面积并相加得到所需面积。

（2）坐标法。通过对一个不规则的几何图形测出该图形边界转折点的坐标值，再用下列公式计算：

式中， ， 为转折点的横纵坐标值， 为转折点的数目，也即多边形边数，当 时， ， 。

1.2等高线法

当地面起伏较大、坡度变化较多时，可采用等高线法估算土方量。利用现成的绘有等高线的地形图，计算等高线所围得面积，再根据两相邻等高线的高差按以下公式计算土方量：

， ——相邻等高线所围面积；

——相邻等高线间的高差。

1.3方格网法

大面积的土石方估算常用该法，适用于地形起伏较小、坡度变化平缓的场地。这种方法是将场地划分成若干个正方形格网，然后计算每个四棱柱的体积，从而将所有四棱柱的体积汇总得到总的土方量。具体步骤如下：

1.3.1绘制方格网，并求格网点高程点。首先建立地形的坐标方格网，方格网的一边与地形等高线或场地坐标网平行，大小根据地形变化的复杂程度和设计要求的精度确定，边长一般常采用10 ×10 或20 ×20 （地形平坦、机械化施工时也可采用50 ×50 ）。

1.3.2确定场地平整的平均高程。水平面的设计高程等于场地地面高程的平均值，在方格网中四个角点的高程只用了1次，边上各点的高程用了2次，网格内拐点处用了3次，网格内各点高程用了4次，根据方格顶点的地面高程及其在计算每格平均高程时用到的次数求加权平均值，即为所求平均高程 ：

式中， 为方格总数。

1.3.3计算挖、填方高度。用方格顶点高程减去设计高程，得到每一方格点的挖、填方高度，即

挖填高度 =

“+”表示挖方高度，“-”表示填方高度，挖填方高度应标注在相应方格点右下方。

1.3.4计算挖、填土方量。根据绘制好的方格网点依次计算每个方格点的土方量，每个方格点的土方量等于挖方面积（填方面积）乘以平均挖方高度（填方高度），也可根据角点、边点、拐点和中心点的挖填高度，分别代表1/4，2/4，3/4.4/4方格面积的平均挖、填方高度，按下式分别计算：

角点：挖（填）方高度 ×1/4放方格面积；

边点：挖（填）方高度 ×2/4放方格面积；

拐点：挖（填）方高度 ×3/4放方格面积；

中心点：挖（填）方高度 ×4/4放方格面积；

若方格内既有挖方又有填方，分别计算出挖方和填方量，再求所有方格点挖方和填方累加总和即为总挖方量和总填方量。

1.4 DTM法

数字地面模型（Digital Terrain Model，DTM）是用一群地面点的平面坐标和高程描述地表形状的一种方式。地表任一特征内容如土壤类型、植被、高程等均可作为DTM的特征值，以高程为特征值的DTM也称为数字高程模型（Digital Elevation Model，DEM）。DEM是用数字形式 ， ， 坐标来表达区域内的地貌形态，以缩微的形式再现了地表形态起伏变化特征，因此只需在计算区建立两个DTM，一个为原始地表DEM，另一个为设计地表DEM，根据两个DEM的差即可求出计算区的土方量。周越轩（2000）认为土方计算可按下述方法进行：

设原始地表DEM为DEM ，设计地表DEM为DEM ，在相同的坐标原点和格网分辨率的条件下，将同一区域的DEM 和DEM 进行叠加，可得一新的DEM，设为 DEM，则有 DEM=DEM -DEM ，其分量表示式为

式中： 表示地表DEM的格网点高程； 表示设计DEM的格网点高程。

对任一格网点 ，若 ，则该格网为挖方；若 ，则该格网为填方。设方格网面积为 ，则该方格网处的土方量为：

分别对 和 的数据进行累加，即可求得该区域的填挖方量。

1.5平均高程法

平均高程法就是在测量时每隔20 测1个碎步点，把所有碎步点的高程相加求平均值，即作为该测量区域的平均高程，再借助CAD等辅助工具求得面积，即可求出土方工程量。平均高程法没有考虑挖填方，误差较大，但在实际中施工单位往往多采用这种计算方法。

2土方量计算方法比较分析

由于断面法、等高线法适用于地形变化较大的地形，实际应用最多的土方量多发生在平原地区，下面就用DTM法、方格网法及平均高程法计算实例来比较分析各自的特点。由于数据庞大，工作量较大，借助南方CASS7.0的相应功能计算土方量。

2.1 DTM法

2.1.1 DTM法计算XX地工程建筑实例。

利用DTM方法对XX地的施工开挖实例分析，借助计算机辅助功能将测量数据处理后的都的结果为为挖方量165122.7 ，填方量1187.4 。如图1

图1 DTM法操作步骤

2.2 方格网法

2.1.1 方格网法的实例计算

针对同样的施工场地继续利用方格网法进行计算，当方格宽度为5 时，软件计算结果为挖方量165034.4 ，填方量1126.1 ；当方格宽度为10 时，软件计算结果为挖方量164763.6 ，填方量1270.7 。如图2

图2 方格网法操作步骤

2.3平均高程法

由CAD软件可知土方范围线面积为18149.76 ，经计算土方范围线内所有上标高为178.576 ，设计标高为169.00 ，由土方工程量计算公式 得

土方挖方量 ，填方量为零。

2.4比较分析

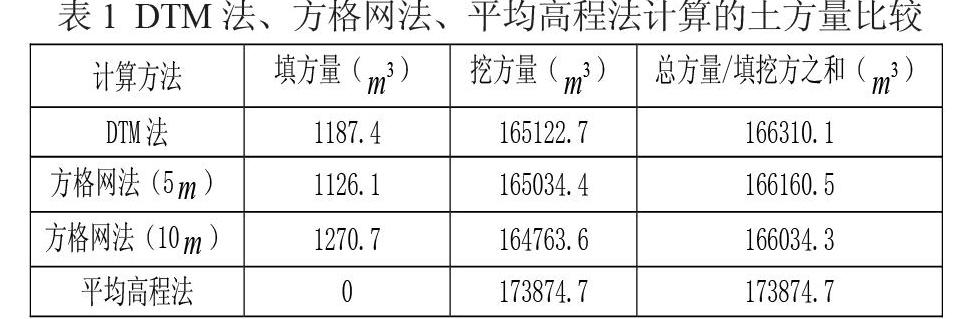
表1 DTM法、方格网法、平均高程法计算的土方量比较

计算方法 填方量（ ）

挖方量（ ）

总方量/填挖方之和（ ）

DTM法 1187.4 165122.7 166310.1

方格网法（5 ）

1126.1 165034.4 166160.5

方格网法（10 ）

1270.7 164763.6 166034.3

平均高程法 0 173874.7 173874.7

由表1可以看出，如果以三种方法的平均值作为土方量的最或是值，则DEM法的误差为1.06%，5米方格网法误差为1.15%，10米方格网法误差为1.23%，平均高程法误差为3.44%。由此可见，DEM法与方格网法不相上下误差较小，平均高程法误差较大，方格网法与格网宽度有关，格网宽度越小精度越高，一般5米为最佳格网宽度。

实际上，对于中、小型建设项目，旧城区改造以及高差不太大的地形场地的土方量的计算，施工单位及造价咨询单位多采用平均高程法计算、核对土方工程量。根据上述研究结果表明平均高程法误差较大，DTM法及方格网法适宜土方量的计算，但DTM法及方格网法并没有考虑实际地形地貌、是否放坡、开挖要求等实际情况，而且实际土方量数据庞大、工作强度高，这就需要寻找一种适合施工单位能够快速、准确的计算土方量的方法。

3土方量计算方法改进分析

由于土方量计算量大、工作繁重的特点，依然借助南方CASS7.0的相关功能实现土方量的计算机自动化，用计算机代替人工，能极大提高工作效率，又能减少计算过程误差。软件DTM法和方格网法计算过程中设计高程均是手动输入，所以在已知设计高程时选择DTM法最佳，当测绘院给出原始地貌标高和开挖后下标高数据时，DTM法就无法计算土方量，因此寻求基于三角网规则的方格网法来计算土方量。

3.1上、下标高均为高程数据时的计算方法。

1、将上、下标高分别生成数据文件。具体步骤为工程应用→高程点生成数据文件→有编码高程点→选取高程点的范围→选取建模区域边界→生成数据文件。

2、将下标高生成三角网文件。具体步骤为文件→新建图形文件→绘图处理→展高程点→输入绘图比例尺→输入坐标数据文件→注记高程点的距离（直接回车）→等高线→建立DTM→输入坐标文件名，自动生成sjw格式三角网文件。

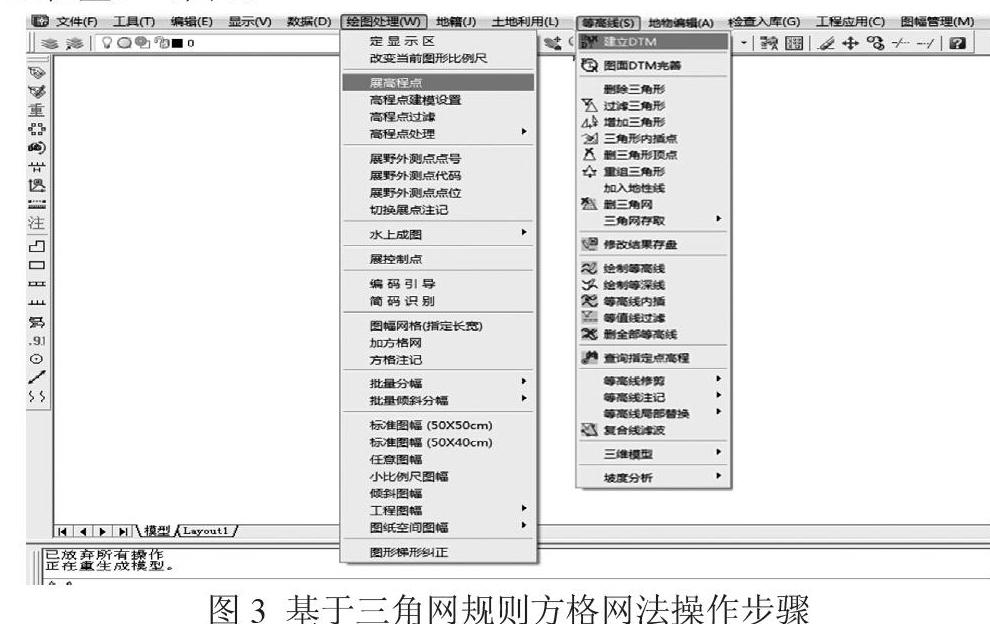
3、基于三角网规则方格网法计算土方量。具体步骤为工程应用→方格网法土方计算→选择计算区域边界线→输入上标高坐标数据文件→设计面输入三角网文件→方格宽度5 ，即可求得土方工程量。（图3）

图3 基于三角网规则方格网法操作步骤

基于三角网规则的方格网法既考虑原始地形地貌又考虑开挖后地形地貌变化，计算结果更符合实际，而且借助软件的处理可快速实现土方量的计算，大大节省了算量时间。

图4 土方量计算分部示意图

在实际施工过程中，土方开挖往往分为三部分（图4）道路工程量、边坡工程量和主楼工程量。原始地貌标高和道路标高往往均是由专业测绘院进行测量整理出高程数据，基底标高也即设计标高根据主楼基础标高而定，道路工程量适宜采用基于三角网规则的方格网法计算，主楼工程量适宜采用DTM法计算，DTM和方格网法均可考虑放坡可用来计算边坡土方量。

由于道路工程量和主楼工程量直上直下挖填，用基于三角网规则的方格网法和DTM法计算结果真实可靠；软件计算放坡面时设定放坡角度，默认放坡面非常平整，这不符合实际情况，而且边坡各处放坡宽度、角度也不一样，边坡的不规则使边坡工程量成为土方计算最难的部分。

经过研究分析，软件可以计算出原始地貌标高、道路标高、基底标高，所以很容易求出标高差，只需求得上底面积和下底面积即可根据公式

求得边坡工程量，上下底面积可根据平均顶口宽和平均底口宽利用CAD偏移功能，再用多段线圈出上下底面积范围线求得。建议施工单位在计算边坡土方量时实测实量边坡底口宽和边坡顶口宽，这样求得边坡工程量更符合实际。

4结论

以上介绍了工程土方量计算中的断面法、等高线法、方格网法、基于数字高程模型（DTM）法及平均高程法的基本原理、方法，并对比分析了常用DTM法、方格网法及平均高程法，结合土方实际情况探索出适合施工单位使用的快速、准确计算土方量的计算方法。通过分析比较，笔者认为将土方量按实际情况分为道路工程量、主楼工程量、边坡工程量三部分，并分别采用基于三角网规则的方格网法、DTM法及平均值法能够最快、最准确求得土方工程量。

参考文献

[1]周越轩、刘学军、杨治洪，基于DTM的土方工程量计算与精度分析[J].长沙交通学院学报，2000，16（4）；39-43。

[2]罗德仁、邹自力、汤江龙，工程土方量计算比较分析[J].东华理工学院学报，2005，28（1）；59-64。

[3]张超、王秀茹、郭晓辉、李素云，平原区土地整理中的土方量计算方法比较[A].水土保持研究，2008，15（3）；84-87。

[4]張婷婷、王铁良，土方量计算方法研究，安徽农业科学报，2006，34（22）；6047-6050。