金沙水电站鱼道水力特性数值模拟
2015-10-21黎贤访
黎贤访
(长江勘测规划设计研究院,湖北 武汉 430010)
金沙水电站位于金沙江干流中游末端的攀枝花河段,工程任务以发电为主,兼有供水、改善城市水域景观及对下游水电站的反调节作用等。拦河筑坝势必阻断鱼类在金沙江的洄游通道,造成鱼类生存环境破碎,需在枢纽中布置鱼道等过鱼设施。
鱼道利用鱼类喜迎逆流的生物学特性,使用多级隔板阻流在通道形成适宜的流速区,以诱导鱼类上溯。鱼道过鱼的水流条件涉及水深、宽度、流速、流态、泥沙含量、水质等诸多因素,其中水力特性以考察流速分布和流场形态为主。20世纪80年代,Rajaratnam等[1-2]通过试验研究了竖缝式鱼道水池长宽比、水池底坡坡度与水流流态的关系。法国的Larinier等[3]提出了鱼道水池单位体积消能率的概念,以表征鱼道中水流的紊动强度。目前,国内外学者基于CFD数学模型针对鱼道水力特性的研究逐渐丰富[4-5],为合理布置鱼道提供了有益的启示。
结合国内外鱼道水力学研究成果[6-8],以金沙水电站鱼道初步设计型式为原型建立CFD数学模型[9],模拟鱼道水流的流场形态及流速分布,分析鱼道布置型式的合理性。
1 过鱼对象
根据文献资料,金沙江中游干支流分布有鱼类149种,特有鱼类52种。金沙水电站主要过鱼对象有胭脂鱼、圆口铜鱼、长薄鳅、长鳍吻鮈、岩原鲤、鲈鲤、四川白甲鱼等。针对上述鱼类的游泳能力进行室内试验,结果如表1所示。
鱼道的设计流速主要根据主要过鱼对象的克流能力而定,金沙江中下游主要鱼类的初步克流能力试验成果表明,鱼类上溯的临界流速约1.5 m/s。参考上述试验结果,金沙水电站鱼道的设计流速取1.1 m/s。
2 过鱼池型式
根据枢纽的调度方案,设计鱼道运行水深在1.5~3.0 m之间。鱼道断面为矩形,为兼顾表层、中层和底层鱼类上溯,采用同侧竖缝式隔板;过鱼池底板为斜坡,坡比 i=1∶58;鱼道净宽B取3.0 m。鱼道隔板等间距分布;鱼道池室长度(亦即隔板间距)按l=(1.2~1.5)B计算,取3.6 m;竖缝导向角为45°。初步设计得出的鱼道隔板型式及尺寸如图1所示。

表1 临界速度测试样本及测试结果

图1 隔板型式及尺寸(单位:mm)
垂直竖缝式鱼道的流量按式(1)作近似计算[4]。计算得出,鱼道的流量在0.430~0.993m3/s之间。

式中,Q为鱼道流量,m3/s;μ为 垂直竖缝的流量系数,取值范围0.65~0.85;b为竖缝宽度,m;H1为竖缝上游的池室水深,m。
鱼道水流的湍流强度过大,对鱼类的上溯游动产生不利影响。为确保水池中的低湍流度流动,水池的大小满足容积功率耗散E<150 W/m2。鱼道池室的容积功率耗散的计算公式[4]为

式中,E为容积功率耗散,W/m2;ρ为水的密度,kg/m3;B为过鱼池宽度,m;hm为水池中的平均水深,m;lb为过鱼池长度,m;d为隔板厚度,m。按式(2)计算得出鱼道池室的容积功率耗散约为21.76W/m2,紊动不剧烈,适合鱼类上溯。
3 CFD数值模拟
3.1 数学模型
3.1.1 控制方程组
基于RNG k-ε湍流方程[5]建立鱼道连续池室的数学模型,控制方程组如下:
动量方程:

式中,ui、uj为流体微元的速度分量;P为流体的压强;ν为流体的运动黏度;k为紊动动能;ε为紊动耗散率;μeff为等效紊动粘度;Gk为平均速度梯度引起紊动动能k的源项;Gb为浮力引起紊动动能k的源项;YM为可压缩紊流中脉动扩张对整体紊动耗散率的贡献;C1ε、C2ε、C3ε为经验常数;σk、σε分别表示与k、ε对应的prandtl数;Sk、Sε为自定义源项;Rε为增项。
3.1.2 计算网格、边界条件及数值方法
方程的离散采用四面体网格的有限体积法,并在竖缝周边区域进行局部加密处理,如图2所示。

图2 计算网格
模型上游、下游边界分别采用鱼道设计流量和设计水深;过鱼池上部出口的运动流体为空气,采用恒定压力边界条件p=0;池室边壁采用无滑移壁面条件。过鱼池自由水面模拟使用VOF法[8]。压力计算采用PRESTO格式插值,动量、体积分数等均采用一阶迎风格式插值,压力和速度的耦合采用SIMPLE算法。模型数值计算的时间步长取0.1 s,计算历时延长至流量、水位计算结果基本恒定。
3.2 结果分析
取鱼道最大设计水深Hmax=3.0 m和最小设计水深Hmin=1.5 m两组工况开展数值模拟。对计算结果截取平行于鱼道底面的斜截面作分析,斜截面相对池底的高度与设计水深之比h/H分别为0.2、0.5、0.8。斜截面流速等值线如图3所示。
根据模拟结果,过鱼池水流呈现如下特征:①相邻过鱼池的流速分布相似,竖缝泄流沿疏缝导向前进,两侧形成比较明显的回流区;②相邻竖缝泄流的主流区域首尾相连,形成了明显“S”形的主流速区;③上、中、下层截面的流速分布形态基本相同;④池室水深1.5 m相对池室水深3.0 m,流速分布形态相似,竖缝流速较大。
沿竖缝垂向中心线的流速分布见图4,可知,流速大小随水深增加逐渐增大;H=1.5 m时,竖缝流速为0.81~1.40 m/s;H=3.0 m时,竖缝流速为0.73 ~1.08 m/s。
计算结果表明:①竖缝流速未超过1.5 m/s,鱼类可以克流上溯;②竖缝流速呈“表层小,底层大”的渐增型分布,适合不同游泳能力的鱼类分层通过;③竖缝间水流形成连贯的主流区,可以诱导鱼类连续上溯;④水深较小时,竖缝流速相对较大,不利于游泳能力较弱的鱼类上溯。

图3 流速等值线
4 结论
基于金沙水电站水情及鱼类资料,对金沙水电站鱼道开展了水力学设计,并建立CFD数学模型对鱼道水流作数值模拟和分析。根据计算结果,鱼道竖缝的最大流速低于鱼类的极限流速,过鱼池段形成了适宜不同游泳能力的鱼类上溯的连贯通道。研究表明,金沙水电站鱼道的初步设计型式和尺寸较合理,满足鱼类上溯的水力学要求;鱼道在幼鱼上溯期间,宜增大池室的水深。
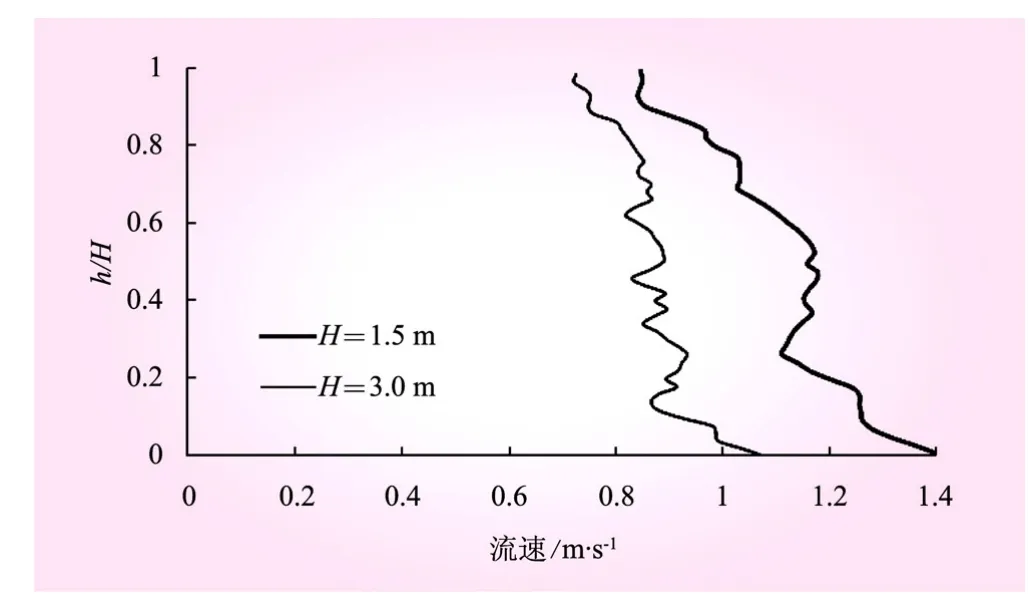
图4 沿竖缝垂向中心线流速分布
[1]RAJARATNAM N,Van der VINNE G,KATOPODIS C.Hydraulics of Vertical Slot Fishways[J].Journal of Hydraulic Engineering,1986,112(10):909-927.
[2]RAJARATNAM N,KATOPODIS C,SOLANKI S.New designs for vertical slot fishway[J].Journal of Civil Engineering,1992(19):402-414.
[3]LARINIER M,TRAVADE F,PORCHER J P.Fishways:biological basis,design criteria and monitoring[M].Food and Agriculture Organization of the United Nations,2002:54-57.
[4]徐体兵,孙双科.竖缝式鱼道水流结构的数值模拟[J].水利学报,2009,40(11):1386-1391.
[5]曹庆磊,杨文俊,陈辉.同侧竖缝式鱼道水力特性的数值模拟[J].长江科学院院报,2010,27(7):26-30.
[6]SL 609—2013 水利水电工程鱼道设计导则[S].
[7]德国水资源与陆地改良学会.鱼道——设计、尺寸及监测[M].北京:中国农业出版社,2009.
[8]徐海洋,魏浪,赵再兴,等.大渡河枕头坝一级水电站鱼道设计研究[J].水力发电,2013,39(10):5-7.
[9]王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.
[10]郭坚,苪建良.以洋塘水闸鱼道为例浅议我国鱼道的有关问题[J].水力发电,2010,36(4):8-10,19.
