时域采样定理MATLAB实现

吴顺喜 李坤 赵聪 黄文晋 邓文博 严东

【摘 要】取样定理是把模拟信号变成数字信号取样频率选取的一条重要准则。对连续信号进行等间隔采样形成采样信号，采样信号的频谱是原连续信号的频谱以采样频率为周期进行周期性延拓形成的。本文选取一模拟信号， 在 Matlab平台上用不同的取样频率对其采样，利用MATLAB实现连续信号采样、频谱分析和采样信号恢复，计算在临界采样、过采样、欠采样三种不同条件下恢复信号的误差，从而验证时域采样定理。

【关键词】时域采样定理 连续信号 频谱分析仪 MATLAB

从模拟信号到数字信号，即从连续信号到离散信号的转换都是通过离散采样完成的，采样频率就是每秒钟采样的个数。根据香农采样定理，要保证信号不失真，采样频率要大于信号最高频率的两倍。

1 采样定理介绍

假设离散时间信号 是通过对连续时间信号 取样获得

取样定理的叙述为： 如果 在 > 时 ， = 0， 则连续时间信号 完全可以由离散时间信号重建恢复 ， 其充要条件是：取样频率 ≥2 ； = 2被称为连续时间信 号的奈奎斯特 （Nyquist） 频率。当 <2时 ， 则会在进行 频谱复制时产生重叠 ， 通常称为混叠 （Aliasing）， 则连续时间信

号不能由它的取样信号重建恢复。

2 运用MATLAB举例分析

下面选定一个连续信号，计算在临界采样、过采样、欠采样三种不同条件下恢复信号的误差，从而验证时域采样定理。

f1 = 'sin（2*pi*60*t）'

fs0 = caiyang（f1，40）； %频率fs<2fmax，欠采样

fr0 = huifu（fs0，40）；

Fs1 = caiyang（f1，120）； %频率 fs=2fmax， 临界采样

fr1 = huifu（fs1，120）；

fs2 = caiyang（f1，160）； %频率 fs>2fmax， 过采样

fr2 = huifu（fs2，160）；

2.1创建一个caiyang.m文件

function fz = caiyang（fy，fs）

fs0 = 10000； tp = 0.1；

t = [-tp：1/fs0：tp]；

k1 = 0：999； k2 = -999：-1；

m1 = length（k1）； m2 = length（k2）；

f = [fs0*k2/m2，fs0*k1/m1]；

w = [-2*pi*k2/m2，2*pi*k1/m1]；

fx1=eval（fy）；

FX1 = fx1*exp（-j*[1：length（fx1）]'*w）；

figure

subplot（2，2，1），plot（t，fx1，'r'）

title（'原信号'），xlabel（'时间t（s）'）

axis（[min（t），max（t），min（fx1），max（fx1）]）

subplot（2，2，2），plot（f，abs（FX1），'r'）

title（'原信号幅度频谱'），xlabel（' 频率f（Hz）'）

axis（[-100，100，0，max（abs（FX1））+5]）

Ts = 1/fs；

t1 = -tp：Ts：tp；

f1 = [fs*k2/m2，fs*k1/m1]；

t = t1；

fz = eval（fy）；

FZ = fz*exp（-j*[1：length（fz）]'*w）；

subplot（2，2，3），stem（t，fz，'.'），

title（'取样信号'），xlabel（'时间t（s）'）

line（[min（t），max（t）]，[0，0]）

subplot（2，2，4），plot（f1，abs（FZ），'m'）

title（'取样信号幅度频谱'），xlabel（'频率f（Hz）'）

2.2创建一个huifu.m文件

function fh = huifu（fz，fs）

T = 1/fs； dt = T/10； tp = 0.1；

t = -tp：dt：tp； n = -tp/T：tp/T；

TMN = ones（length（n），1）*t-n'*T*ones（1，length（t））；

fh = fz*sinc（fs*TMN）；

k1 = 0：999； k2 = -999：-1；

m1 = length（k1）； m2 = length（k2）；

w = [-2*pi*k2/m2，2*pi*k1/m1]；

FH = fh*exp（-j*[1：length（fh）]'*w）；

figure

subplot（2，1，1），plot（t，fh，'g'），

st1 = sprintf（'由取样频率fs = %d'，fs）；

st2 = '恢复后的信号'；

st = [st1，st2]；title（st），xlabel（'时间 t（s）'）

axis（[min（t），max（t），min（fh），max（fh）]）

line（[min（t），max（t）]，[0，0]）

f = [10*fs*k2/m2，10*fs*k1/m1]；

subplot（2，1，2），plot（f，abs（FH），'g'）

title（'恢复后信号的频谱'），xlabel（'频率f（Hz）'）

axis（[-100，100，0，max（abs（FH））+2]）；

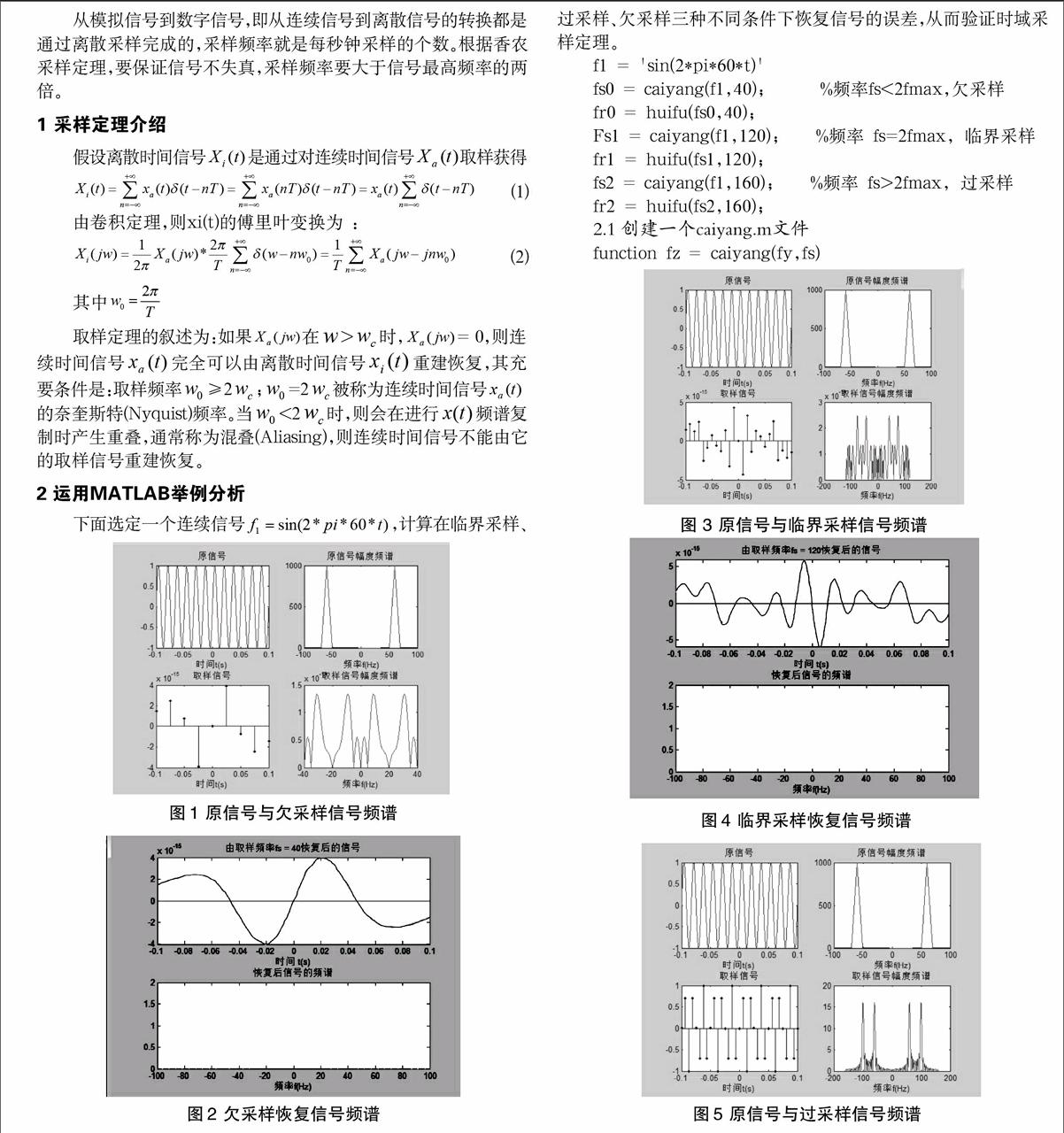
下面是利用MATLAB分析的图1-图6：

从图1、图3、图5的连续傅里叶变换可以看出，信号f1的频率为60Hz、，如果采样频率f≥120Hz就可满足时域采样定理。图2、图4、图6分别为当采样频率为40Hz、120Hz、160Hz时采样恢复后的信号频谱，当f≥120Hz时，信号无明显失真；而f<120Hz时，不满足取样定理，恢复后的信号频谱失真。

3 结语

取样定理表明，在一定条件下，一个连续时间信号完全可以用该信号在等时间间隔上的采样值来表示，并且可以用这些采样值把信号完全恢复过来。这样，采样定理为连续时间信号与离散时间信号的相互提供了理论依据。在数字信号处理技术广泛应用的今天，连续时间信号的离散处理显得日益重要。

参考文献：

[1]吴兆雄.数字信号处理[M].北京：国防工业出版社，1985 .

[2]楼顺天，李博菡.基于 MATLAB 的系统分析与设计 ———信号处理[ M] .西安：西安电子科技大学出版社，1999.

[3]伯晓晨，李涛，刘路.MATLAB 工具箱应用指南[M].北京：电子工业出版社，2000.

[4]范影乐，杨胜天，李轶.MATLAB 仿真应用详解[M].北京：人民邮电出版社 ，2001.