基于参考信号频域半盲提取的机械故障特征声学诊断
2015-10-20羿泽光
羿泽光,潘 楠,刘 凤
(昆明理工大学机电工程学院,云南昆明 650500)
机械设备运转时,其振动信号中蕴含着很多状态信息,尤其是当设备出现故障时,振动特征信号内会产生明显的冲击成分,由此衍生的声信号特性将随之发生改变[1]。机械设备故障诊断能否顺利进行很大程度上依赖于能否从繁多复杂的机械状态信号中提取足够数量且能够真实而客观地反映诊断对象工况的信息[2]。声信号测试具有非接触测量、测试方式简便、在线测试和无附着物影响等诸多优点,尤其适用于工业现场状态监测与故障诊断[3]。然而实际声场环境复杂多变,待识别信号(故障源信号)常与各种干扰信号或噪声相互混杂,无法被有效辨识[4]。因此,为了准确提取机械故障特征,需要将这些噪声抑制或排除,随后根据故障征兆识别故障原因[5]。
近年来,能够在几乎没有任何先验知识的情况下,从混合信号中恢复或估计出源信号的盲信号处理技术为机械故障信号的提取提供了一个有力的解决手段[6-7]。然而,传统的盲分离算法在应用到机械声信号处理时往往无法满足现实情况,不能有效进行机械故障特征的识别与提取,而盲解卷积算法则更适用于实际工业声场环境[8-11]。因此,本文尝试以频域盲解卷积算法为基础,基于全局寻优能力较强的人工鱼群算法,构建针对故障信号特征的多尺度形态学滤波器,最大程度削弱背景噪声干扰;结合机械零部件结构参数构建参考信号,进而通过单元参考信号约束半盲提取算法,逐段进行复分量盲分离;利用改进KL距离解决复分量间次序不确定性问题,最终实现实际声场环境中的故障特征提取。
1 频域盲解卷积基本模型
基于文献[3]的论述,可将频域盲解卷积算法的基本步骤整理如下。
通过加窗短时傅里叶变换(STFT)将拾取到的时域观测信号转换到频域中;此时,时域卷积混合就被转换成为对应频域上各频段的瞬时混合,从而引入复数盲分离算法对源信号进行估计。针对子信号输出次序不确定性问题,将估计的复数信号分频段进行重排序,通过加窗逆短时傅里叶变换(ISTFT)将信号转换回时域,最终得到估计信号。
机械系统产生的信号多种多样,加之设备所处环境中的背景噪声干扰,使得频域盲解卷积算法应用于实际复杂声场中针对机械故障特征的提取时存在很多问题[12-16]:
1)机械声场较为复杂且具有多源干扰,故障特征声易淹没在较强的高斯噪声、复杂周期信号及其他非平稳信号之中,无法被有效识别;
2)声学传感器(传声器)不同于振动传感器,其安装位置与故障源距离较远,声信号在传输过程中容易因长卷积而发生衰减,以致算法求解的复杂度不断增加;
3)使用频域盲解卷积算法提取故障特征信号时,循环部分卷积误差和次序不确定性等固有问题均会影响分离性能;
4)传统频域盲信号处理算法往往无法直接适用于机械故障声振信号的提取。
2 参考信号约束频域半盲提取故障声信号
针对前文所述问题,通过对原有频域盲解卷积算法的各项步骤进行改造优化,降低背景噪声及凸显特征频率范围,将其应用到现实声场故障特征提取之中。
2.1 构造改进多尺度形态滤波器
2.1.1 形态滤波简介
近年来,能够提取信号细节和抑制干扰噪声形态滤波也被逐渐应用于机械声振信号背景降噪[17]。其滤波器结构都是基于差值滤波器或者形态开-闭(OC)和闭-开(CO)平均组合,且多为单一结构元素[18]。然而,实际工业声场中往往不止存在某一种干扰噪声,且信号中的噪声通常是随机的,需要使用多尺度的不同结构元素构建形态滤波器,以避免较严重的滤波器输出统计偏移。
2.1.2 人工鱼群算法优化结构元素
形态滤波的结构元素构成包括形状、幅值和尺寸等多个方面。实验结果表明,半圆形结构元素能够较好地滤除随机噪声,三角形结构元素对于脉冲噪声的滤波效果较好。为了避免目标寻优过早地进入局部收敛,特采用基于集群体智能思想的人工鱼群算法进行全局寻优,将经过均值化处理后的观测信号中相邻峰值间隔的最大值和最小值通过极值寻优,确定结构元素的长度;随后,根据信号峰值的最大值和最小值确定高度范围;最后,将相应的结构元素尺寸分别代入半圆形和三角形结构公式,计算出对应的结构元素集合。整个算法流程如图1所示。
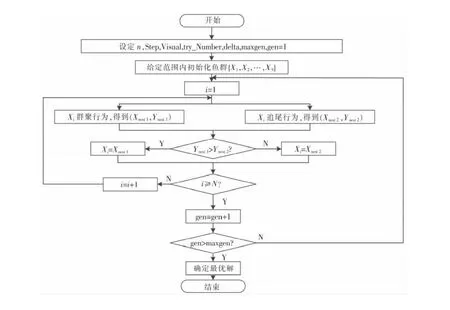
图1 人工鱼群算法寻优流程Fig.1 Flow of improved multi-scale morphological filtering algorithm
图1中:N为人工鱼群大小;{Xi}为人工鱼个体的状态位置;Yi=f(Xi)为第i条人工鱼当前所在位置的实物浓度;Visual为人工鱼的感知距离;Step为人工鱼移动的最大步长;delta为拥挤度;n为当前觅食行为次数;gen为迭代次数;maxgen为最大迭代次数。
2.1.3 改进多尺度形态滤波
闭运算可以较完整地提取信号中的正脉冲,平均组合形态滤波器则可以同时抑制信号中的正负脉冲噪声;但由于在形态联级中使用相同尺寸的结构元素,容易导致滤波器输出统计偏移较为严重[17],因此需构建多尺寸、多结构联级而成的结构元素闭-开组合形态滤波器。式(1)中:8和Θ分别表示膨胀和腐蚀运算。

整体改进多尺度形态滤波算法流程如下:
1)对观测信号x(t)进行均值化处理,同时构建初始化多尺度元λg;
2)计算观测信号的局部极大值和极小值,确定结构元素的高度和长度集合;
3)将计算的高度和长度代入三角形和半圆形结构元素公式,构造结构元素集合;
4)代入式(1)得到y(n)组合滤波器集合;
5)采用人工鱼群算法对滤波器集合进行寻优,使用y(n)对观测信号x(t)进行滤波处理,直至得到最终去噪信号。具体流程见图2。
2.2 参考信号约束半盲提取算法
为了减少算法复杂度,常针对机械设备故障诊断过程中重点关注的包含零部件故障特征频率的低频包络周期信号,通过匹配关键零部件结构参数,基于先验知识构造出理论上的参考信号。以此参考信号为约束,将观测信号与构造参考信号进行相似性度量,进而提取有限数量的估计信号,此即称为半盲提取。仅利用单个参考信号提取估计信号的情况称之为单元参考信号约束半盲提取,即转换为式(2)的约束问题[20]:

约束条件:

式中:J(y)为ICA算法的负熵目标函数;ε(y,r)表示观测信号与参考信号的相似性测度;ξ为区分估计信号与其他信号的阈值,其选取为渐变适应过程,在保证约束目标函数有解的前提下同时避免陷入局部最优。
将式(2)写为无约束拉格朗日函数:
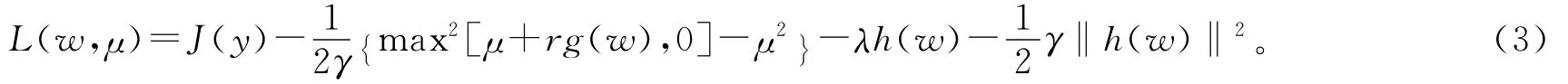

图2 改进多尺度形态滤波算法流程Fig.2 Flow of improved multi-scale morphological filtering algorithm
式中:μ和λ为拉格朗日乘子;γ为尺度惩罚参数。通过对式(3)的极值进行求解,即可得到牛顿迭代算法:

式中:η为学习率;Rxx为混合信号的协方差矩阵;G′y,G″y2和g″y2(wk)分别表示Gy与gy(wk)的一阶导数和二阶导数;μ和λ由式(6)求得:

当信号经过白化与中心化处理之后,=1,则式(4)可写为如下形式:

2.3 解决次序不确定性问题
距离是衡量2个信号相似性的测度,距离越大,说明2个信号相似性越小;距离越小,则说明2个信号相似度越大。距离互参数法的基本原理是通过比较距离,将每个频率段的输出调整至同一通道对应着同一源信号。
高阶统计量信息较二阶统计量如相关系数等更能清晰地反映信号的统计特性,改进KL距离可被用以更好地描述相邻2个频率段内2个复值信号对应概率密度之间的距离:
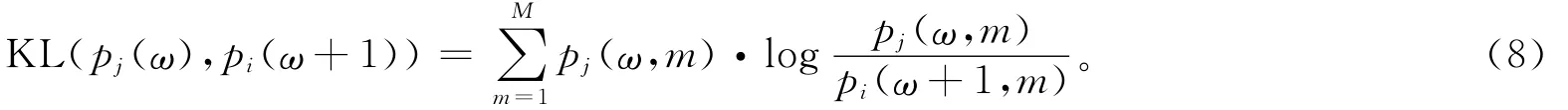
为了验证改进KL距离在复分量相似测度计算上的优势,特进行如下仿真:分别利用改进KL距离及常被用于计算谱聚类的余弦测度(相似度),对18组复分量进行相似度聚类计算。从聚类散点图(见图3)可以看出,利用改进KL距离求解的距离聚类散点线性程度较佳,且其运算速度较基于余弦测度的算法快近50%。

图3 相似度聚类效果对比Fig.3 Comparison of similarity clustering effects
2.4 算法整体步骤
综合前文所述,现将参考信号约束频域半盲提取算法整体执行步骤归纳如下:
1)初始化零部件结构参数,根据结构参数计算特征频率,构造参考信号r(t),随后对观测信号x(t)进行中心化处理;
2)利用改进多尺度形态滤波器对x(t)进行噪声抑制,得到滤波后的信号~x(t);
3)使用STFT将信号~x(t)及r(t)转换到频域中,得到其在频域的表现形式X(ω,t),R(ω,t);
4)利用单元参考信号约束半盲提取算法,使用复分量间改进KL距离进行相似度测量,对X(ω,t)进行逐段复数盲提取,得到与参考信号R(ω,t)相似度最高的各频段复值估计信号Y(ω,t);
5)通过ISTFT将信号转换回时域,最终得到时域估计信号Y(t),求解估计信号的包络解调谱,对特征频率进行分析,进行故障判断。
3 实验验证
为验证本文提出算法的实际效能,于现实声场环境中构建实验装置,以轴承故障特征信号为约束进行半盲提取实验。本次实验使用故障类型未知的NU205滚动轴承作为诊断对象,其相关物理参数如表1所示。

表1 故障滚动轴承参数Tab.1 Parameters of the rolling bearing with fault
将轴承外圈固定,内圈随轴旋转。使用NI CRIO 9082及相关控制模块,配合NI-9234四通道采集模块和3个声望MPA416 1/4英寸TEDS传声器(频率响应范围为20Hz~20kHz)组成嵌入式采集装置。利用LabVIEW开发平台编写测试程序进行信号采集,由于轴承故障频率多集中在低频段,故采样频率设置为8 192Hz,算法由Matlab进行编写。工况及轴承故障特征频率如表2所示。

表2 实验工况及轴承故障特征频率Tab.2 Operation condition and bearing failure frequencies in experiment
所有传声器均距地面高度1m摆放并指向轴承座方向,其中传声器1与传声器2互呈90°,传声器3垂直试验台摆放。传声器探头距离试验台边缘的直线距离分别为0.64,1.81,1.5m,并未采用“抵近测量”原则及吸音板等辅助材料,以期尽量贴近现实工况环境,试验台及传声器的位置关系如图4所示。
开启试验台驱动电机后触发采集程序进行声信号数据采集,采集完毕后通过Matlab从稳态运行情况下的原始数据中截取8 912点数据(1s)进行分析。图5为传声器拾取到3路信号的时域波形及幅值谱。由图5可见,3路信号互相混杂在一起,唯有电机转频信号谱线(13Hz)隐约可见,故障冲击信号已被干扰噪声完全淹没。

图4 试验台及传声器位置关系图Fig.4 Position chart of test-rig and microphones

图5 观测信号Fig.5 Measurement signals

图6 基于FCM模糊聚类的时域盲解卷积算法分离结果Fig.6 Signals separated by the time-domain blind deconvolution algorithm based on FCM
与本文提出算法的提取效果进行对比,首先使用文献[11]提出的基于FCM模糊聚类的时域盲解卷积算法对观测信号进行处理,步长为2,聚类个数设置为3,算法提取结果如图6所示。经该算法运算,得到3个估计信号,但从图6a)中未能发现明显冲击成分,在对应包络谱(图6b))中第2个分离信号虽可以发现13Hz处谱线,但其他故障特征频率并没有得以体现。随后利用本文提出的参考信号约束频域半盲提取算法对观测声信号进行处理,算法步骤如2.4节所述,其中STFT分帧长度设置为512,加汉宁窗,窗长512,窗口移动长度64。分别选用三角形和半圆形结构元素,利用人工鱼群算法构建多尺度形态滤波,对观测信号进行背景降噪。算法提取结果如图7所示。图7a)为时域波形,利用光标对图7b)第1个分离信号的包络谱数据进行读数,可明显发现65,130,195Hz 3条谱线(分辨率f=1Hz),通过对比表2中轴承故障特征频率可知,其与外圈特征大致吻合。由此可判断故障所在,拆解轴承后发现轴承外圈出现裂纹故障(如图8所示),与声学分析诊断结果相吻合。

图7 参考信号约束频域半盲提取算法分离结果Fig.7 Signals separated by reference signal frequency domain semi-blind extraction method
4 结 语
针对目前机械声信号盲提取所面临的多种问题,提出了一种基于参考信号约束频域半盲提取的机械故障特征声学诊断算法,详细介绍了人工鱼群算法、参考信号构建、半盲提取算法、改进KL距离等关键技术的原理与应用,滚动轴承故障声信号半盲提取实验证明了该算法的有效性和实用性。

图8 轴承外圈裂纹故障示意图Fig.8 Schematic diagram of bearing outer crack fault
[1] 王华民,陈霞,安钢,等.基于高阶累积量的齿轮箱故障诊断研究[J].机械强度,2004,26(3):247-249.
WANG Huamin,CHEN Xia,AN Gang,et al.Fault dlagnosis of gearbox based on higher order cumulants[J].Journal of Mechanical Strength,2004,26(3):247-249.
[2] 何正嘉,陈进,王太勇,等.机械故障诊断理论及应用[M].北京:高等教育出版社,2010.
HE Zhengjia,CHEN Jin,WANG Taiyong,et al.Mechanical Fault Diagnosis Theory and Application [M].Beijing:Higher Education Press,2010.
[3] 潘楠,伍星,迟毅林,等.基于频域盲解卷积的机械设备状态检测与故障诊断[J].振动与冲击,2012,31(12):34-41.
PAN Nan,WU Xing,CHI Yilin,et al.Mechanical equipment status detection and fault diagnosis based on frequency domain blind convolution[J].Journal of Vibration and Shock,2012,31(12):34-41.
[4] 潘楠,伍星,迟毅林,等.欠定盲解卷积用于滚动轴承复合故障声学诊断[J].振动、测试与诊断,2013,33(2):284-289.
PAN Nan,WU Xing,CHI Yilin,et al.Underdetermined blind convolution is used for rolling bearings composite fault acoustic diagnosis[J].Journal of Vibration,Measurement &Diagnosis,2013,33(2):284-289.
[5] 李豫川,伍星,迟毅林,等.基于形态滤波和稀疏分量分析的滚动轴承故障盲分离[J].振动与冲击,2011,30(12):170-174.
LI Yuchuan,WU Xing,CHI Yilin,et al.Based on the morphological filter and sparse component analysis of the rolling bearing fault separation[J].Journal of Vibration and Shock,2011,30(12):170-174.
[6] NIKOLAOU N G,ANTONIADIS I A.Application of morphological operators as envelope extractors for impulsive-type periodic signals[J].Mechanical Systems and Signal Processing,2003,17(6):1147-1162.
[7] GELLE G,COLAS M,DELAUNAY G.Blind source separation applied to rotating machin-es monitoring by acoustical and vibrations analysis[J].Mechanical Systems and Signal Processing,2000,14(3):427-442.
[8] ROUTRAY A D,DASH N.Robust preprocessing:Denoising and whitening in the context of blind source separation of instantaneous mixtures[C]∥2007 5thIEEE International Conference.[S.l.]:[s.n.],2007:377-380.
[9] THEODOR D P.Blind separation of vibration signals and source change detection:Application to machine monitoring[J].Applied Mathematical Modelling,2010,34:3408-3421.
[10]KOLDOVSKY Z,TICHAVSKY P.Blind instantaneous noisy mixture separation with best interference-plus-noise rejection[J].Lecture Notes in Computer Science,2007,4666:730-737.
[11]王宇,伍星,迟毅林,等.基于盲解卷积和聚类的机械弱冲击声信号提取[J].振动工程学报,2009,22(6):620-624.
WANG Yu,WU Xing,CHI Yilin,et al.Weak transient impulse signal extraction based on blind deconvolution and cluster in acoustical machine diagnosis[J].Journal of Vibration Engineering,2009,22(6):620-624.
[12]PAN N,WU X,CHI Y L,et al.Application of frequency-domain blind deconvolution in mechanical fault detection[J].Applied Mechanics and Materials,2011,134:2128-2132.
[13]DOUGLAS S C.Fixed-point fast ICA algorithms for the blind separation of complex-valued signal mixtures[C]//Conference Record of the Thirty-Ninth Asilomar Conference on Signals,Systems and Computers.[S.l.]:[s.n.],2005:1320-1325.
[14]LAN X,ZHANG Y G,KASSAM S A.Robust source separation using ranks[C]∥Proceedings of the Tenth IEEE Workshop on Statistical Signal and Array Processing.[S.l.]:[s.n.],2000:324-328.
[15]REJU V G.Partial separation method for solving permutation problem in frequency domain blind source separation of speech signals[J].Neurocomputing,2000,71(10/11/12):2098-2112.
[16]MAZUR R,MERTINS A.An approach for solving the permutation problem of convolutive blind source separation based on statistical signal models[J].IEEE Transactions on Audio,Speech and Language Processing,2009,17(1):734-739.
[17]沈路,周晓军,张文斌,等.广义数学形态滤波器的旋转机械振动信号降噪[J].振动与冲击,2009,28(9):70-73.
SHEN Lu,ZHOU Xiaojun,ZHANG Wenbin,et al.Denoising for vibration signals of a rotating machinery based on generalized mathematical morphological filter[J].Journal of Vibration and Shock,2009,28(9):70-73.
[18]沈路.数学形态学在机械故障诊断中的应用[D].杭州:浙江大学,2010.
SHEN Lu,Study on Application of Morphology in Machinery Fault Diagnosis[D].Hangzhou:Zhejiang University,2010.
[19]潘楠,羿泽光.基于频域盲信号处理的汽车制动异响定位方法研究[J].河北科技大学学报,2014,35(5):410-416.
PAN Nan,YI Zeguang.Study of brake abnormal sound localization method based on frequency-domain blind signal processing[J].Journal of Hebei University of Science and Technology,2014,35(5):410-416.
[20]许海翔,丛丰裕,史习智.基于复信息量的频域多通道盲解卷积算法[J].数据采集与处理,2008,23(3):278-283.
XU Haixiang,CONG Fengyu,SHI Xizhi.Frequency domain multi-channel blind solution of convolution algorithm based on the complex information[J].Journal of Data Acquisition and Processing,2008,23(3):278-283.
