基于饱和度的BRT车站物理停靠泊位设置方法研究

2015-10-20车丽彬鄢勇飞

城市道桥与防洪 2015年9期

关键词：子站泊位排队

车丽彬,鄢勇飞,蒋乐

(武汉市政工程设计研究院有限责任公司,湖北武汉 430023)

基于饱和度的BRT车站物理停靠泊位设置方法研究

车丽彬,鄢勇飞,蒋乐

(武汉市政工程设计研究院有限责任公司,湖北武汉 430023)

运用排队理论模型,基于停靠泊位饱和度,提出了BRT车站物理停靠泊位数计算与分组设置方法。首先计算单个泊位的最大车辆通行能力,通过控制车队长和排队概率来确定泊位的设计饱和度,然后根据设计饱和度计算对应的设计有效泊位数,最后通过不同组合核算确定子站与泊位数个数。实例表明该方法可以为BRT车站物理停靠泊位设计提供依据。

BRT车站；饱和度；停靠泊位；子站

0 引言

为解决城市交通拥堵,越来越多的城市开始规划建设快速公交(Bus Rapid Transit， BRT)系统, BRT车站是其重要组成部分之一,也是影响BRT系统通行能力的重要环节。BRT车站停靠泊位个数与车辆的通行能力密切相关。现有文献大多从车站位置、容纳线路能力、关键站点的通行能力、有效泊位数等方面进行研究［1-9］,对如何确定车站所需的物理停靠泊位个数的研究很少,快速公交系统设计规范［8］也只给出停车泊位数范围值,而在BRT系统规划设计中物理停靠泊位数是重要的前置设计参数,应根据站台客流和线路等参数进行计算。采取不恰当的BRT车站设计规模会导致站台的闲置或者出现车辆的严重排队。运用排队理论模型,通过控制车站内车辆队长和排队概率来确定泊位的设计饱和度,提出了基于饱和度的BRT车站物理停靠泊位计算方法,并对子站分组设置方法进行了探讨,对BRT车站的规划和设计具有借鉴意义。

1 有效停靠泊位及单个停靠泊位通行能力

对于直线式停靠站,随着停靠位数量的增加,其有效停靠位边际增量递减,虽然对有效泊位数有不同的取值,总体而言,当停靠位数量超过3个时,通行能力提升非常有限［9-10］,如表1所示,需要进行分组设置站台,但没有给出分组设站和和确定车站物理泊位数的方法。

表1 车站有效停靠泊位数一览表

文献［9］给出了一个停靠泊位每小时通过的最大车辆数计算公式：

式中：g/c为每个信号周期有效绿灯时间；tc为连续两辆公交车之间的时间间隔；td为每辆车平均停留时间；Za为公交车站排队概率的一维正态变量；cv为停留时间的偏差系数。文献［11］也给出了单个停靠泊位的车辆通行能力C0计算公式：

式中,R为补偿停留时间和到达波动因子折减系数,取0.833；与式(1)的td含义相同。在计算停靠泊位的车辆通行能力时都需要考虑交叉口绿信比(包括具备信号优先条件)的影响,同时对车辆停留时间的偏差与波动进行适当的修正。为便于比较,本文采用上述两种方法计算单个停靠泊位通行能力。

2 相关参数

2.1 泊位饱和度

根据排队论基本理论,BRT车辆进出车站过程可以简化为车站“服务机构”对车辆“顾客”的服务系统,如图1所示。

图1 BRT车站排队系统过程示意图

泊位饱和度即服务强度ρ［2］［12］,由车辆平均到达率与泊位的服务速率之比确定,ρ要小于1才能保证排队系统的稳定,否则将形成无限的队列。

式中：λ为车辆平均到达率，veh/h,即单位时间内平均到达车辆的车辆数；μ为泊位服务速率,veh/h,即单位时间内服务(或通过)的最大车辆数,是服务时间的倒数。

为了尽量减少车站的车辆排队,需要将泊位饱和度控制在合适的范围,否则将在车站形成排队［13］。

2.2 实际到达车辆数

对于停靠线路数为L的BRT车站,其车辆到达数N与线路的发车频率F有关,同时与上游交叉口绿灯时间相关。因此,单位时间内到达车站的车辆数应小于基于计划发车频率的车辆数。假设各线路发车频率相同,则所有线路车辆总的到达率为：

考虑到BRT具备公交信号优先权,取值略高于常规值。

2.3 车辆平均停留时间

BRT车站采用站台售检票模式,且满足乘客水平乘降,可提高乘客上下车效率,减少车辆停留时间。车辆在车站停留时间等于在最繁忙车门为乘客服务的时间加上开、关车门所需时间［2］,计算公式为：

式中：ρa、ρb为高峰小时内每辆车从最繁忙车门下车和上车的乘客数；ta、tb为乘客下车和上车时间；toc为开关门时间,一般取2～5 s。对于新建车站,可采用每辆车平均上下车人数和平均上下车时间计算乘客服务时间,平均上下车人数可根据车辆乘客更新系数［10］计算得到。

2.4 车辆排队模型运行指标

对于单个停靠泊位,车辆排队模型运行指标为：

式中：P0为泊位上没有车辆的概率；Pn为泊位上有n辆车的概率；Ls为系统队长的平均值；Lq为系统中正在排队等待的车辆数。

3 物理停靠泊位计算与设置方法

Step1根据排队模型,由式(6)～式(9)分别计算Pn、Ls和Lq。

Step2对于单个停靠泊位,为减少排队,要求Ls≤2和Lq≤1,且要求停靠泊位有2辆车的概率小于15%,由此确定设计饱和度ρ。

Step3根据设计饱和度ρ,计算对应的有效停靠泊位数Es=N/(COρ)。

Step4核算子站与泊位数的不同组合是否满足所需的有效泊位数,并根据设计条件确定最优组合,即可得到车站物理停靠泊位设置方案。

4 实例分析

以武汉市雄楚大街BRT静安路车站为例［14］,根据客流预测和公交线路调整方案,车站需要停靠线路条数为L=11条,每条线路平均发车频率F=20 veh/h,上游交叉口的绿信比g/c为0.7,由式(4)计算到达车站的车辆数N为154 veh。

公交车为18 m长的低地板车型,载客量为120人,假定车辆在车站的乘客更新系数取20%,乘客平均上下车时间取0.8［9］,toc取3 s,由本文2.3节中方法计算td为22.6 s,车辆消散时间tc取15 s。由step1计算不同饱和度取值下单个泊位内车辆数概率、系统队长平均值和正在排队的平均长度指标,见表2所列。

结合表2,由step2得到设计饱和度应小于0.6。再由step 3计算对应有效泊位数,表3列出了不同饱和度下的有效泊位值,可知在设计饱和度小于0.6的条件下,车站有效泊位数不应小于4个。

比较表3计算结果,根据式(2)计算的单个停靠泊位的可容纳车辆数要大于式(1),但差别不明显。随着饱和度的增加,单个泊位所能容纳的车辆也会增加,所需有效泊位数减少,但会增加车辆的排队长度,如表2所列。同时,由表1可知道,当物理停靠泊位数超过3个时,其有效泊位数只有2.45-2.65,因此应分组设置子站。采取随机到达模式计算,要满足至少4个有效泊位数,子站及物理泊位数组合如表4所列。

表2 不同饱和度下单个泊位的车辆数概率及排队指标值一览表

表3 不同饱和度下有效泊位数计算值一览表

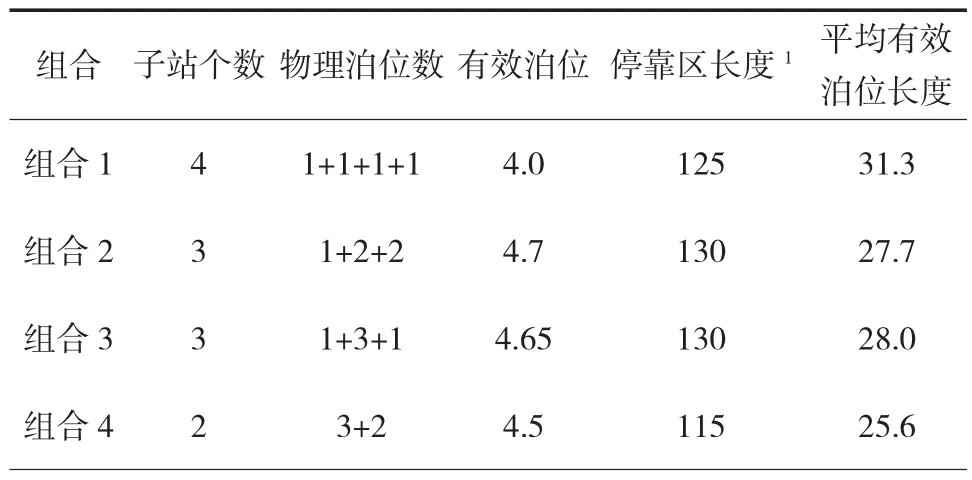
表4 分组子站及物理泊位数组合情况一览表

比较表4可知,为满足有效泊位数要求,共需要设置4～5个物理停靠泊位。组合1中每个子站的物理泊位都得到最大利用,但子站个数太多,平均有效泊位长度最大；组合2比组合1总长增加5 m,但可增加0.7个有效泊位,组合2比组合3更加经济有效；组合3和组合4都设置有3个泊位的子站,增加了子站车辆停靠位置的随机性,会增加乘客走动距离,但后者比前者更经济有效,当条件受限时可选择后者。综合比较,每个子站设置不超2个泊位是比较合理的,当道路条件受限(如站台总长受边界条件限制)时,子站可设置3个泊位。

实例中组合2和组合4均是经济可行方案,最终从通行能力和道路限制条件方面考虑选择组合2,即设置3个子站,子站泊位数采取1+2+2组合形式,其有效泊位数为4.7个,可满足要求。如果要求排队长度更小,则需降低泊位设计饱和度,但会增加子站和物理泊位个数,而且饱和度偏小会造成停靠泊位资源的得不到有效利用。

5 结论

对于BRT系统,车站物理停靠泊位数是影响系统通行能力的重要设计参数。现有研究侧重于研究车站通行能力,但很少对BRT车站物理停靠泊位规模进行研究,在工程实践中大多采用经验值［8，15］,缺少计算依据。以排队论为基础,通过控制车辆队长和排队概率来确定泊位设计饱和度,再结合单个泊位可容纳的车辆数计算所需的有效泊位数,并探讨了分组子站与停靠泊位设置方法,为BRT车站停靠泊位设计提供借鉴。

［1］彭国雄，莫汉康. 城市公交停靠站设置常见问题及对策［J］.交通运输工程学报， 2001,1(3)：77-80.

［2］柏海舰，李文权. 常规公交站台容纳线路能力计算模型［J］.东南大学学报(自然科学版)， 2007,37(6)：1077-1080.

［3］张卫华. 城市快速公交(BRT)专用道客运能探讨［J］，武汉理工大学学报(交通科学与工程版)， 2008，32(1)：118-121.

［4］马莹莹，杨晓光，马万经. 快速公交站台形式及位置最佳布置方法［J］，城市交通，2006，4(4)：50-54.

［5］张洋，赵一新，付晶燕.快速公交专用车道及站台布设模式选择［J］.城市交通， 2009，7(3)：27-34.

［6］于洋，何世伟.基于乘客换乘量和停车泊位的BRT站台规模研究［J］.重庆交通大学学报(自然科学版)，2008，27(4)：634-638.

［7］龚翔，陈学武，李娅.城市快速公交停靠站点在交叉口的选址研究［J］.土木工程学报，2011，44(11)：115-120.

［8］ CJJ136-2010,快速公共汽车交通系统设计规范［S］.

［9］ TRB. Highway Capacity Manual［R］.Washington， D.C.: TRB，National research council， 2000.

［10］ Kittelson & Associates. TCRP100: Transit Capacity and Quality of Service Manual， 2nd Edition ［R］， Washington， D.C.: TRB， 2003.

［11］ Roger P. Roess， William R. McShane & Elena S. Prassas. Traffic Engineering， 2nd 、Edition［M］， United States， Prentice Hall， 1998.

［12］盛志前，张颖颖，赵杰.快速公交车站饱和度指标取值探讨［J］.城市交通，2007，5(1)：25-29.