基于Petri网的测试路径生成方法研究
2015-10-19李柱
摘要:随着软件规模的扩大和复杂度的增加,如何实现高效的软件测试,成为决定软件测试效率的关键。Petri网作为一种适合于描述异步并发现象的系统模型,具有系统描述及强大的行为分析功能。本文通过对Petri网、可达树特点的分析的基础上,提出一种基于Petri网的软件测试路径生成方法,并将该方法用于等边三角形判定程序测试路径生成中,能够有效的生成测试路径并提高了软件测试的效率。
关键词:Petri网;可达树;测试路径生成
中图分类号:TP393 文献标识码:A 文章编号:1009-3044(2015)20-0026-03
Research on the Method of Test Path Generation Based on Petri Net
LI Zhu
(Chongqing Jiaotong University, Chongqing 400074, China)
Abstract: With the expansion of software scale and complexity of software, how to achieve high efficiency of software testing is the key to determine the efficiency of software testing. As a kind of system model which is suitable for describing asynchronous and concurrent phenomena, Petri net has the function of system description and powerful behavior analysis. Based on Petri nets and reachability tree analysis ,this paper proposed a software testing path generation method based on Petri net, and used the method for an equilateral triangle decision procedure test path generation, can effectively generate test paths and improve software test efficiency.
Keywords: Petri net ; reachability tree; test path generation.
1 概述
随着信息时代的到来,计算机软件得到广泛普及,人们对软件的需求越来越高,这也就导致软件的复杂度和规模越来越大。而如何对软件进行有效的测试就成为人们关注的焦点。
软件测试的关键一步就是软件测试路径的生成,目前已有很多测试路径的生成方法,作者本人曾将遗传算法用于测试用例的生成并进行了改进[1];李鹏、彭祥伟等提出一种基于状态图的测试路径自动生成方法[2],并可实现对路径的优化;赵磊、伦立军等提出一种基于软件体系结构的测试路径生成方法[3],该方法在Wright语言的基础上,根据BG图构造基于覆盖准则的测试路径,生成测试数据。
然而,以上测试路径生成方法仍有一些不足:(1)路径生成方法过于复杂,不便于操作;(2)生成的路径存在循环路径,没有进行约束,导致工作量增加。
Petri网是Carl Adam Petri 在其论文“Kommunikation mit Automaten”中首次提出,是一种描述异步、并发计算机系统模型。Petri网既可采用数学表述方式,也可利用直观的图形表达方式,其丰富的系统描述手段和系统行为分析技术为计算机科学的部分学科的发展提供了坚实的理论基础。因此本文将Petri网用于测试路径的生成,并利用可达树进行论证,保证了测试路径生成的效率及效果。
2 Petri网及可达树概述
2.1 Petri网的定义[4]
Petri网是一种图形化的形式化语言表示法,它采用具有形式语义的图形语言,而图形化表示法便于理解,适合各种水平人员的使用,成为一种通用的形式化语言表达方法。下面给出Petri网的基本定义:
满足下列条件的三元组PN=(P,T,F)称为一个Petri网:
1)P为非空有限的库所组成的集合;
2)T为非空有限的变迁组成的集合;
3)[F?(P×T)?(T×P)]是库所、变迁的流关系;
4)[dom(F)?cod(F)=P?T]
其中:
[dom(F)=x∈P?T|?y∈P?T:(x,y)∈F] [cod(F)=x∈P?T|?y∈P?T:(y,x)∈F]
2.2 Petri网的可达树分析方法
之所以将Petri网用于测试路径的生成,很大原因是由于其具有丰富的图形表示及分析方法。Petri网分析方式包括进程网、状态方程及可达树等,此处我们采用可达树分析法实现对上述生成的Petri网的分析。
可达树分析法[5]是一种对Petri网图和其对应程序进行验证的重要方法,Petri网的可达树集合是指在使能情况下运行Petri网可到达的结点的集合。可达集由变迁点火产生的标记来描述可达树中的结点,弧标记变迁点火,从源结点开始,产生树中的每个新结点。下面给出产生可达树的Petri网结构图(图1)如下所示:
图1 产生可达树的Petri网结构图
下面将该Petri网的可达树生成过程介绍如下:
当t1、t2点火时,产生的可达树如下所示。其中(1,0,0)作为源结点,在源结点t1点火,产生标记(1,1,0),t2点火,产生标记(0,1,1)(图2)。接着新产生的标记(1,1,0)分别针对t1、t2点火产生标记(1,2,0)和(0,2,1)。以此类推,产生该Petri网图的所有的可达树结点,效果图(图3)如所示:
图2 初始点火状态下的结点变化
图3 Petri网产生的所有可达树结点效果图
3 基于Petri网的测试路径生成
软件测试的定义各种各样,但简而言之,软件测试即贯穿于整个软件开发生命周期中的对软件进行分析、设计、程序验证(verifiCation)和确认(validation)的活动过程,其目的是通过发现软件的缺陷和错误,以提高软件的质量并验证软件的质量满足用户的需求的程度。
3.1 程序基本语句的Petri网描述[6]
软件测试成败的关键就是测试路径的生成,鉴于Petri网在异步并发及形式化描述方面的优势,很多专家学者将其应用于软件测试路径的生成。基于Petri网的测试路径生成,首先需要将被测程序转化为其对应的Petri网图。为便于描述,下面利用Petri模拟工具PIPE2.5将软件程序常用基本语言及其Petri网描述如下:
1)顺序语句的Petri网描述:
语句1;
语句2;
2)If-else语句的Petri网描述:
if(条件语句)
语句1;
else
语句2;
3)Switch语句的Petri网描述:
switch(跳转语句)
{
case 1: 语句1;
case 2: 语句2;
…
case n: 语句n;
case n+1: 语句n+1;
}
4)for的Petri网描述:
for(初始语句;循环语句;结束语句)
{
语句1;
语句2;
}
3.2 基于Petri网的三角形判定程序测试路径生成
为方便描述,下面给出三角形判定程序的Java程序代码,如下所示:
import java.util.Scanner;
public class SanJiao{
public static void main(String[] args) {
int n=100;
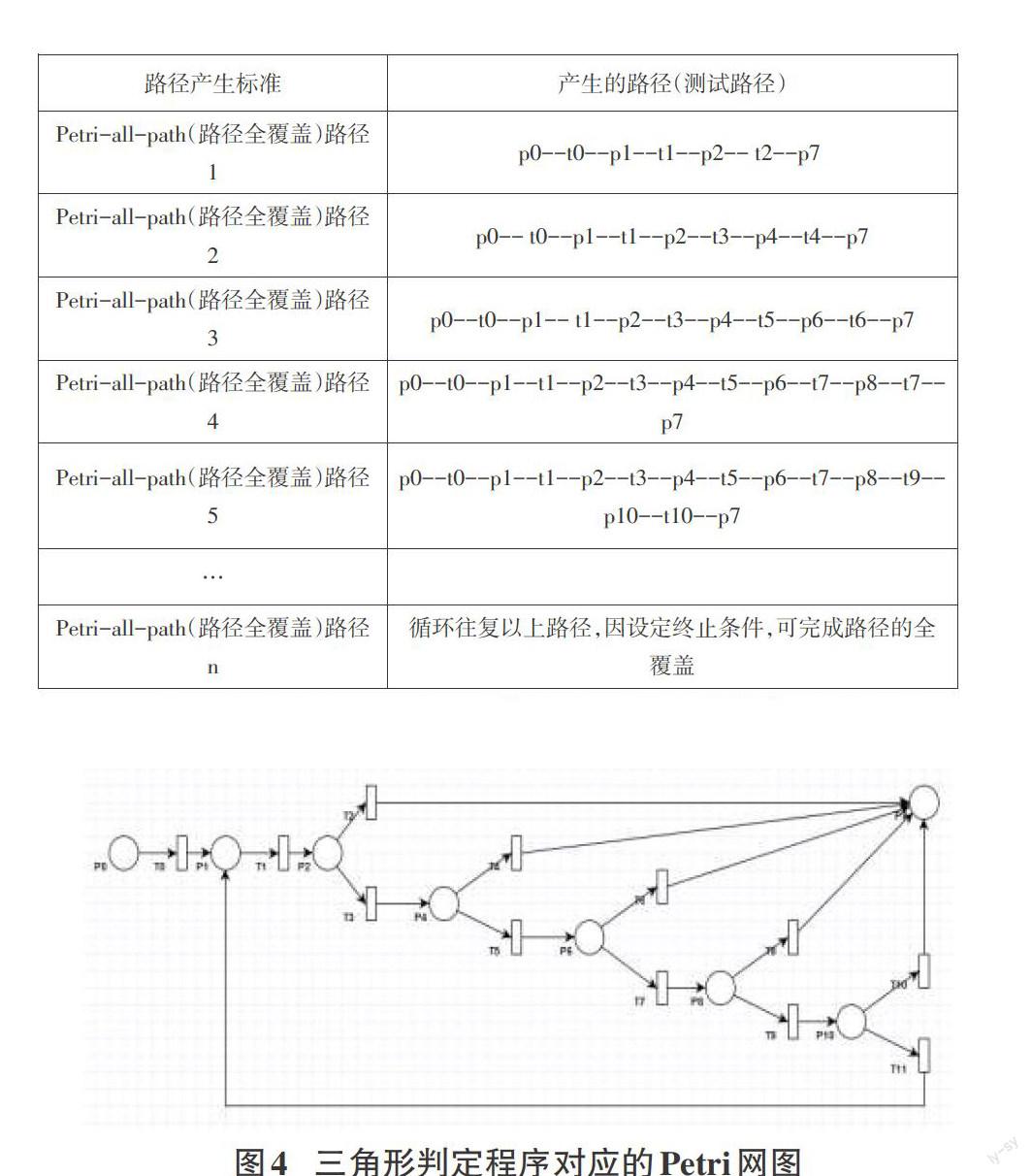
for(int i=1;i Scanner sc=new Scanner(System.in); System.out.println("请输入三角形的三个边:"); double a=sc.nextDouble(); double b=sc.nextDouble(); double c=sc.nextDouble(); if(a>0&&b>0&&c>0){ if((a+b<=c)||(a+c<=b)||(b+c<=a)){ System.out.println("这不是三角形!"); }else if(a==b && b==c){ System.out.println("这是等边三角形!"); }else if(a==b||b==c||a==c){ System.out.println("这是等腰三角形!"); }else if(a*a==b*b+c*c || b*b==a*a+c*c || c*c==a*a+b*b){ System.out.println("这是直角三角形!"); } else System.out.println("这是一般三角形!"); }else System.out.println("输入数据有错误,请输入大于0的数!");}}} 对于以上的三角形判定程序实是在对程序数据流及控制流分析的基础上,描绘出该段程序的Petri网图(如图4所示)。下一步需要对该段程序的Petri网图进行分析得出其可达标识集,再结合变迁的引发序列来表示每条路径是否被测试到,即得到该段测试程序的测试路径集,最终完成整个软件的测试。
图4 三角形判定程序对应的Petri网图
由可达树的产生过程我们可以看出,新结点产生的过程是可以循环往复的,可能造成可达树是无穷的。因此,我们需要一种限制可达树规模的方法,我们约定:当一个结点没有变迁产生时(称为终止结点),不允许其产生新的结点;可达树中出现过的结点(称为重复结点),不考虑它的后续结点。
下面我们结合可达树生成方法及三角形判定程序生成的Petri网得到该程序的基于数据流的结点可达集,即程序测试路径,详见下表:
[路径产生标准\&产生的路径(测试路径)\&Petri-all-path(路径全覆盖)路径1\&p0--t0--p1--t1--p2-- t2--p7 \&Petri-all-path(路径全覆盖)路径2\&p0-- t0--p1--t1--p2--t3--p4--t4--p7\&Petri-all-path(路径全覆盖)路径3\&p0--t0--p1-- t1--p2--t3--p4--t5--p6--t6--p7\&Petri-all-path(路径全覆盖)路径4\&p0--t0--p1--t1--p2--t3--p4--t5--p6--t7--p8--t7--p7\&Petri-all-path(路径全覆盖)路径5\&p0--t0--p1--t1--p2--t3--p4--t5--p6--t7--p8--t9--p10--t10--p7\&…\&\&Petri-all-path(路径全覆盖)路径n\&循环往复以上路径,因设定终止条件,可完成路径的全覆盖\&]
至此,我们完成了三角形判定程序所有测试路径的覆盖,而以上路径则能够完成程序的完全覆盖,达到程序测试的目的,其他程序的测试均可采用此方法进行路径覆盖。
4 结束语
本文将Petri网用于软件测试程序路径的生成中,将被测程序进行分析得出其Petri网图,然后利用可达树分析法,对Petri网图中存在的路径进行分析提取,实现对被测程序路径的完全覆盖,最终得到测试路径。
参考文献:
[1] 李柱,丁晓明.用于测试用例生成的遗传算法改进[J].科学技术与工程, 2011,11(5):990-991.
[2] 李鹏,彭祥伟,周喜,等.基于状态图的测试路径自动生成 [J].计算机工程,2011,37(2):25-26.
[3] 赵磊,伦立军.基于软件体系结构的测试路径生成方法[J].微电子学与计算机, 2008,25(1):177-180.
[4] 霍敏霞.基于Petri网的并发程序测试路径生成[D].西南大学,2012:7-8.
[5] 翟长勇.基于Petri网的Web应用软件测试技术研究[D].贵州大学,2011:14-17.
[6] 郑艳艳.基于Petri网的模型的GUI软件测试用例生成研究 [D].华中师范大学,2010:17-19.