钻进参数优化研究综述

张奇志，何素素，韩振华

（1.西安石油大学电子工程学院，陕西西安710065；2.陕西省钻机控制技术重点实验室，陕西西安710065）

钻进参数优化研究综述

张奇志1，2，何素素1，韩振华1

（1.西安石油大学电子工程学院，陕西西安710065；2.陕西省钻机控制技术重点实验室，陕西西安710065）

钻进参数优化是钻井工程中的关键技术之一。介绍了现有的钻进参数优化数学模型，并对适用于模型求解的几种常用传统优化算法、人工智能优化算法及改进的混合算法进行了总结分析，最后提出了当前钻进参数优化研究中仍需解决的问题及未来研究趋势。

钻进参数优化；数学模型；智能优化算法

钻井是一个复杂的系统工程，钻进参数优化是钻井工程经典研究内容。钻进参数优化是指在一定的客观条件下，根据不同参数配合时各因素对钻进过程的影响规律，采用科学的最优化方法，选择合理的钻进参数配合，从而使钻进过程达到最优的技术和经济指标［1］。通过研究钻进参数优化，能够缩短钻井周期，降低钻进成本，提高钻进质量和钻进效率，增强钻进的安全性和可控性。

钻进参数的优化研究主要可分为两个方面：一是钻进参数优化模型的建立；善是针对钻进参数优化模型，寻找有效的优化算法进行求解。本文从优化模型的建立和优化算法的选择两方面对钻进参数优化发展过程进行总结分析，并对钻参优化研究方向与发展趋势进行了归纳。

1　钻进参数优化的数学模型

根据最优化理论，要衡量钻井整体技术经济效果，首先要确定目标函数，并将钻进过程的基本规律与之结合起来，建立钻进参数优化模型。由于钻井条件的复杂性，影响因素过多，描述钻进过程的数学模型也是不断发展和完善的。

1.1钻进模型

1.1.1机械钻速模型机械钻速模型是建立最早也是最受关注的钻进模型。

W.C.Maurer方程［2］基于牙轮钻头的破岩机理，在假设井底为完全清洁的理想状态下，建立了机械钻速与钻压、转速、钻头尺寸和地层强度的关系方程，如式（1）：

式中：F为钻头总进尺，m，t为钻时，h，D为钻头直径，mm；V为破岩体积。

该方程结构简单，容易计算，但由于考虑因素过少，其结果的准确性比较低。

E.M.Galle和H.B.Woods［2］是最早研究成本最低的最佳恒定钻压和转速配合的研究者之一。其通过统计大量的现场钻井数据，绘制出了最佳钻压和转速的标准曲线图版，并给出了钻速方程，如式（2）：

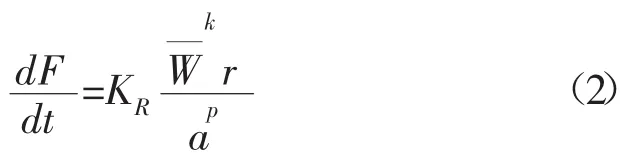
式中：KR为地层可钻性系数；W为钻压，kN；其他参数值均参考文献［2］。

该方程考虑了钻头在不同地层的磨损情况，增加了其结果的可信度；但是其参数取值依赖于数据图版，具有很大的局限性。

Bingham［2］基于实验数据，提出了宾汉钻速方程，如式（3）所示。但其缺点是忽略了水力因素的影响。

式中：α为钻压指数；N为钻速，r/min。

Bourgoyne和Young［2］基于前人的理论基础，从钻井的多个角度出发，把钻速预测模型描述为多个影响因素之间的线性组合，建立了包含8个机械钻速影响因素的参数方程。这是迄今为止业界提出的考虑最为全面且应用范围最广的钻速方程之一，简称B-Y模型，具体如式（4）：

式中：f1～f8分别为地层可钻性、钻井深度、岩层致密性、井底压差、钻头直径和钻头承重、转速、牙齿磨损、水力参数对钻速的影响。

该方程适用于牙轮钻头和PDC钻头，且针对不同类型的循环介质可适当调整参数项；具有不固定的表达式，所有参数项都是根据所研究区域的钻井和地层数据回归分析得到的，更具实用性和准确性。但其缺点在于：虽然描述较为全面，但是为钻井数据的采集带来了较大的困难，尤其是需要实时采集的数据。

目前，应用较广泛的机械钻速模型是修正的杨格机械钻速模型［1］。该模型是在杨格机械钻速模型的基础上，综合考虑了钻压、转速、钻头牙齿磨损、水力因素、钻井液性能等因素对钻速的影响，并结合AMOCO研究中心和鲍格因等人的研究结果，最终归纳建立的，如式（5）：

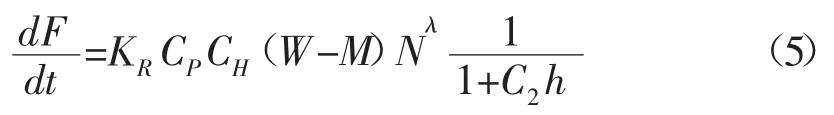
式中：λ为转速指数；CP为压差影响系数；CH为水力净化系数；C2为牙齿磨损系数；h为钻头牙齿相对磨损量，新钻头h=0，全部磨损时h=1。

该模型是根据数学、力学原理和实验而得到的经验公式，解析性较好，且与实际钻井情况的符合率较高。1.1.2其他模型分析研究影响钻头磨损的因素及钻头的磨损规律，对优选钻进参数具有重要意义。常用的牙齿磨损速度及轴承磨损速度方程为：

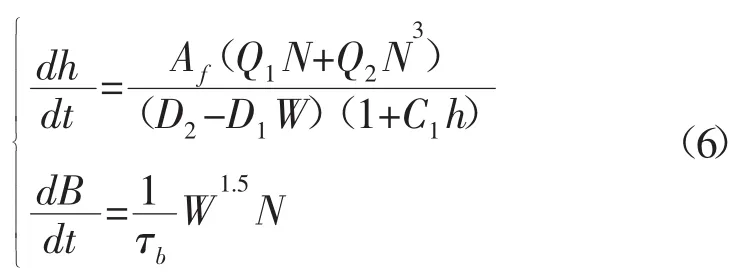
式中：Af为地层研磨性系数；D1、D2为钻压影响系数；Q1、Q2为转速影响系数；C1为牙齿磨损减慢系数；B为轴承磨损量；τb为轴承工作系数。

B-Y模式的牙齿磨损速度及轴承磨损速度方程［2］为：

钻头比能可描述钻头破岩效率，比能越小，钻头的破岩效率越高，即钻头的使用效果越佳。通常采用Teale模型［3］，如式（8）所示，这里不再赘述。

式中：υ是机械钻速，m/h。

1.2目标函数

1.2.1单目标优化数学模型衡量钻井整体技术经济效果的标准有多种类型。传统的单目标钻进参数优化一般都以单位进尺成本作为标准，如式（9）：

式中：C为单位进尺成本（元/米）；Cb为钻头成本（元/只）；Cr为钻机作业费（元/小时）；tt、tc和tb分别为起下钻时间、接单根时间以及钻头工作时间，h。

钻头总进尺F及工作时间t可由修正杨格钻速模型和钻头牙齿磨损速度模型确定，即将式（6）代入（9）中，并经过一定处理，可导出进尺成本目标函数表达式，如式（10）：

在实际工程中，评价钻井方案的优劣，不应局限于一个指标，而应用多个指标来评价。此外，单位进尺成本模型中的成本系数常常受经济因素和法律条文等的影响，复杂多变，不利于纯粹的工程技术和理论研究。

1.2.2多目标优化数学模型文献［4］建立了综合考虑钻井成本和钻速的双目标PDC钻头钻进参数优化模型，该模型引入了钻井成本和钻速权重系数，按照一定的权重对钻井成本和钻速两个目标进行优化，可对不同作业要求下的PDC钻头钻进参数进行优化。其建立的目标函数见式（11）。

式中：m、n分别为钻井成本和钻速的权重系数，0≤m≤1，0≤n≤1，且m+n=1；Cm为指定条件下的最优单位进尺成本，万元/米，υp为指定条件下的最优钻速，m/h。

为了进行多方面的综合考虑，依据实际的钻井过程优化思想，文献［5］以机械钻速最大、钻头寿命最长和钻头比能最小为目标，建立了基于机械钻速、钻头寿命和钻头比能的多目标优化模型。其目标函数如式（12）：

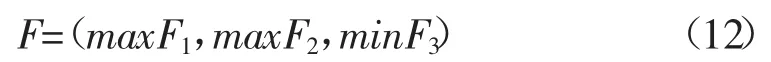
式中，F1表示机械钻速；F2表示钻头寿命；F3表示钻头比能。

2　优化算法

2.1传统优化算法

2.1.1单目标优化钻进参数单目标优化属于非线性优化组合问题，常用的求解方法有经典函数极值法和模式搜索法。陈庭根等［1］提出采用经典极值法，但其数学推导和计算过程比较复杂，需人工干预，设计周期较长、效率低。李士斌等［6］通过群优化搜索实现钻进参数优化罚函数模型的求解。

2.1.2多目标优化传统多目标优化方法分为直接法和间接法。直接法能精确求解出多目标优化的Pareto最优前沿的具体位置，但只适用于满足特定条件的简单多目标优化，局限性大。对于大多数多目标优化问题，传统解法只能使用间接法，通过不同的转换方法把多目标优化变为单目标优化，把单目标优化的解作为多目标优化的有效解。常见的间接法有加权求和法、ε-约束法和极大极小值法等。

2.1.2.1加权求和法加权求和法是给每个目标函数分配权重，然后求和，将多目标优化问题转化为单目标优化［4］，是一种最简单有效地求解多目标优化问题的经典方法，模型构建容易，但权重系数的取值直接影响能否找到令人满意的Pareto最优解，而大多数的实际问题不可能事先知道精确的权值和目标值，只能根据经验人工给出粗略的估计值，求解方法的有效性严重依赖于研究人员对优化问题的了解，缺乏通用性和灵活性。

2.1.2.2ε-约束法ε-约束法的原理是：从m个目标函数中任意取出m-1个目标函数，把这m-1个目标函数通过某种方法转换为约束条件，剩下的单个目标函数作为单目标优化问题来进行求解。这种方法容易实现，但明显的一个缺点就是很难选择合适的εi值，因为不论εi的值怎么变化，总是会改变可行域的范围。

2.1.2.3极大极小值法极大极小值法是在对各个目标来说最不利的情况下，找出最有利的解。选取各目标函数中的最大值，用来构造评价函数，即把求解多目标极小化问题转化为求解数值极小化问题。其数学表达如式（13）：

极大极小值法通常只适用于由最差目标决定系统性能的情况，此时较容易得到较好的解，相反则容易漏选能使其余目标都较优的优化方案。

2.2智能优化算法

智能优化算法又称为现代启发式算法，是一种具有全局优化性能、通用性强且适用于并行处理的算法，包括模拟退火算法、遗传算法、粒子群优化算法等。此类算法一般具有严密的理论依据，而不是单纯凭借专家经验，理论上可以在一定时间内找到最优解或近似最优解。

2.2.1模拟退火算法1983年，S.Kirkpatrick等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，通过赋予搜索过程一种时变且最终趋于零的概率突跳性，从而能有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。但算法的收敛性和收敛速度依赖于退火方案的选择，其参数较难确定［7］。

2.2.2遗传算法（NSGA）遗传算法于1995年由N. Srinivas和K.Deb提出，是通过模拟自然进化过程来搜索最优解的一种随机化搜索方法。该算法在快速找到Pareto前沿和保持种群多样性方面都有很好的效果，是一种有效的自适应优化方法。但NAGA存在非支配排序的时间复杂度大，进化效率和稳定性不高等问题，且计算量大，时间长。

文献［8］采用遗传算法来确定B-Y模型中的系数，这比多元回归分析方法［9］和数学方法求解具有更高的准确性。

伊鹏等［10］针对通用自适应遗传算法进化求解过程稳定性不高，存在局部收敛等问题，将改进自适应遗传算法应用于钻井参数优化设计，但该算法在搜索效率及精度等方面有待提高。

沙林秀等［11］提出了基于斐波那契数列的自适应量子遗传算法，该算法降低了时间复杂度，提高了算法效率，具有收敛速度快、精度高和稳定鲁棒性好等优点。

NSGAⅡ是NSGA的改进算法，是解决多目标优化问题最优秀的进化算法之一。文献［5］采用NSGAⅡ，其基本思想是：首先随机产生种群规模为N的初始种群进行非支配排序，然后通过选择、交叉和变异得到子代种群；从下一代开始，将父代种群与子代种群合并，进行非支配排序，根据个体的拥挤度和非支配关系，选取N个个体组成新一代种群（即新一代的父代种群）；最后，通过选择、交叉和变异操作产生新的一代种群（即新一代的子种群），如此类推，直到满足设定精度结束。

文献［12］采用带精英策略的非支配排序遗传算法来求解基于B-Y模型的多目标优化钻井模型，结果得到了一组较好的非支配Pareto解集。

2.2.3粒子群优化算法粒子群优化算法起源于对鸟类觅食行为的模拟，将每只鸟抽象为一个无质量无体积的粒子，采用简单的速度-位移模型，通过粒子间的合作与竞争而产生的群体智能指导优化搜索，具有较强的鲁棒性和全局搜索能力，且不需要借助所求问题的任何特征信息，是一种高效的并行搜索算法，适用于复杂优化问题的求解。与遗传算法相比，粒子群算法概念简单、收敛速度快、所需调整的参数少、可直接采用实数编码、算法结构简单、容易实现，既适合科学研究，又适合工程应用。

周春晓等［13］利用粒子群算法来求解PDC钻头钻井参数优选目标函数，该算法简单，参数少，具有收敛性强、速度快，且所获得的最优解质量高等诸多优点，但易陷入局部最优。

文献［14］提出一种改进的多目标粒子群算法MOPSO，该算法基于Pareto支配准则，采用外部档案来存储非支配解，使用动态拥挤距离截断来限制外部档案规模，采用变异算子对粒子速度施加扰动，以防止算法陷入局部最优。

2.2.4混合算法由于单个算法总有其优势与缺陷，因而随着各种智能优化算法的发展，通过多个算法的结合，取长补短，提出了各种混合优化算法，如EA与PSO的结合［15］，PSO-GA混合算法［16］，混沌粒子群优化算法等。

3　钻进参数优化研究方向与发展趋势

钻进参数优化具有显著的工程实用意义，通过对数学模型和优化算法的综合分析得出钻参优化的研究方向。

一方面，钻进模型的建立是进行钻参优化的基础，目前选用的模型有些较为陈旧，简单，且形式上具有很强的地域针对性和局限性，模型中的一些参数获取较为困难，在进一步的研究中，希望采用能够综合考虑各种实际因素、具有较强通用性、参数获取较为直接容易的新模型，从而极大的方便现场参数获取与实际优化工作。

另一方面，传统的常规算法已不能满足优化要求，虽然模拟退火、NSGA及粒子群算法等智能优化算法弥补了传统数学优化方法的不足，然而模拟退火算法全局收敛性好，但所需时间长，且随系统规模扩大及复杂性提高而增加；遗传算法虽能以较大概率找到全局最优解，但其局部搜索能力不强，算法复杂度较高；粒子群算法则往往容易陷入局部最优。因此，在钻进参数优化问题的未来研究中，应该从算法本身的改进及利用算法本身的特性混合多种算法的优化策略方面寻找突破。

4　结语

对钻进参数优化的数学模型及优化算法进行了综合分析，介绍了传统优化算法与各种智能优化算法的优缺点，最后提出现有钻参优化研究中仍存在的问题及未来的研究方向。随着研究工作的深入、优化算法的发展，多目标钻进参数优化将为工程优化钻井提供一种新方法和新思路。

［1］陈庭根，管志川.钻井工程理论与技术［M］.山东：中国石油大学出版社，2000.

［2］Eren T.Real-time-optimization of drilling parameters during operations［D］.Middle East Technical University，2010.

［3］樊洪海，冯广庆，肖伟，等.基于机械比能理论的钻头磨损监测新方法［J］.石油钻探技术，2012，40（3）：116-120.

［4］金业权，王茂林.综合考虑成本和钻速的PDC钻头钻进参数优化设计［J］.石油钻探技术，2012，40（5）：13-16.

［5］李琳，聂臻，沙林秀，等.基于NSGA2的钻进参数多目标优化［J］.石油机械，2013，41（3）：55-71.

［6］李士斌，张立刚，荆玲，徐守峰.钻井参数优选新方法［J］.石油钻探技术，2007，35（4）：9-11.

［7］罗陶涛，欧阳伟，王娟.基于模拟退火算法的非线性钻井液流变模式的参数优化［J］.钻井液与完井液，2013，30（4）：29-32.

［8］MH Bahari，A.Bahari，F.Nejati Moharrami and MB Naghibi Sistani.Determining Bourgoyne and Young Model Coefficients Using Genetic Algorithm to Predict Drilling Rate［J］. Journal of Applied Sciences，2008，8（17）：3050-3054.

［9］李昌盛.基于多元回归分析的钻速预测方法研究［J］.科学技术与工程，2013，13（7）：1740-1744.

［10］伊鹏，刘衍聪，郭欣，李进.基于改进自适应遗传算法的钻井参数优化设计［J］.石油机械，2010，38（2）：30-33.

［11］沙林秀，等.基于快速自适应量子遗传算法的钻井参数优化［J］.石油机械，2013，41（2）：32-36.

［12］Guria C，Goli K K，Pathak A K.Multi-objective optimization of oil well drilling using elitist non-dominated sorting genetic algorithm［J］.Petroleum Science，2014，11（1）：97-110.

［13］周春晓，吴兆清，张国辉，谢冬梅.基于粒子群算法的PDC钻头钻井参数优化［J］.中国石油和化工标准与质量，2011，（9）：160-161.

［14］李琳，张栋栋，沙林秀，徐红.基于粒子群算法的钻进参数多目标优化［J］.现代电子技术，2014，37（10）：24-27.

［15］Angeline P.J.Evolutionary Optimization Versus Particle Swarm Optimization.Philosophy and Performance Difference［C］.The 7th Annual Conferenceon Evolutionary Programming，San Diego，USA，1998.

［16］姚坤，李菲菲，刘希玉，等.一种基于PSO和GA的混合算法［J］.计算机工程与应用，2007，43（6）：62-64.

The summary of drilling parameters optimization

ZHANG Qizhi1，2，HE Susu1，HAN Zhenghua1
（1.College of Electronic Engineering，Xi'an Petroleum University，Xi'an Shanxi 710065，China；2.Key Laboratory of Shanxi Province for Drill Control Technology，Xi'an Shanxi 710065，China）

Drilling parameter optimization is a key technology of drilling engineering.This paper introduced several existing mathematical models of drilling parameter optimization，analyed the commonly used traditional optimization algorithm，artificial intelligence optimization algorithm and the improved hybrid algorithm which are applicable to the solution of the model，and finally put forwards the problems still need to study and the future research trend of the drilling parameter.

optimization of drilling parameters；mathematical models；intelligence optimization algorithm

10.3969/j.issn.1673-5285.2015.02.003

TE242

A

1673-5285（2015）02-0008-05

2014－12-23

陕西省教育厅项目“多目标多参量动态优化钻井控制策略的研究”，项目编号：13JS091；西安石油大学研究生创新基金资助项目“基于改进的粒子群算法的钻进参数多目标优化研究”，项目编号：2013cx120323。

张奇志，女（1965-），教授，2011年获得西北工业大学博士学位，现从事电驱动钻机电气控制技术方面的研究工作，邮箱：hesusu13@126.com。