页岩气藏压裂缝网模拟及沟通效果评价

郭小哲，赵 刚

(中国石油大学，北京 102249)

引 言

目前在缝网模型研究中，天然裂缝的模拟多采用离散裂缝网络模型[1－2]，具有较为成熟的理论和工具。在国内压裂缝网的模拟中对砂岩储层[3－5]的研究方法较多，而关于页岩储层的压裂缝网模拟[6－8]研究较少。基于以上分析，设计了一套简便而实用的页岩气藏水平井压裂缝网效果评价系统，该模型可以实现3个方面的研究:模糊的天然裂缝网络理想化模拟和反演;压裂缝网形态模拟和关键约束参数反演;应用新设缝网沟通效果评价指标进行压裂工艺参数的优化。经过现场试验证实了该模型的准确性与适用性。

1 天然裂缝模拟模型

模型中需要把不同大小的裂缝按裂缝组的形式设置于储层中，采用离散裂缝网络模型[9－10]中裂缝片的方法进行天然裂缝的模拟，裂缝的高度为储层的厚度，裂缝位置采用Monte－Carlo模拟方法，裂缝长度按指数分布模拟，开度、方位角和倾角按正态分布模拟[11]。其公式为:

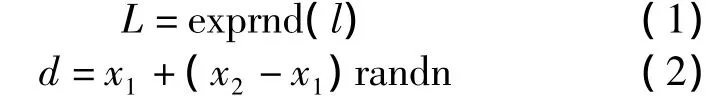
式中:L为模拟裂缝长度，m;l为裂缝平均长度，m;exprnd为随机分布函数;d为模拟裂缝开度值，mm;x1、x2分别为裂缝开度的最大、最小值，mm;θ为模拟裂缝方位角或倾角值，(°);α为裂缝方位角或倾角平均值，(°);σ为方位角或倾角标准差，(°);randn为正态随机分布函数。

在实际模拟过程中可通过测井和露头信息设置具有代表性的模糊天然裂缝组或者假设理想裂缝组，在人工缝网模拟后与微地震结果拟合时，可进一步反演天然裂缝组，取得合理的裂缝参数。对确定性较高的大裂缝可在裂缝系统中直接置入，更实际地模拟储层原始状态。

2 人工压裂缝网模拟模型

页岩气藏中水平井方向一般沿着地层最小水平主应力，在分段压裂过程中会形成由多簇裂缝构成的裂缝网络，在每簇裂缝网络中，人工裂缝与天然裂缝充分沟通，形成储层中的体积缝网。体积缝网的压裂模拟过程包括裂缝宽度计算和裂缝走向计算。

2.1 裂缝宽度计算

裂缝宽度决定着裂缝体积的大小，采用PKN模型计算压裂缝宽[12]，即:

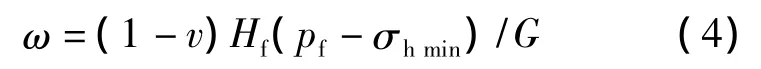
式中:ω为裂缝宽度，m;pf为压裂液压力，MPa;V为泊松比;Hf为储层厚度，m;σhmin为最小水平主应力，MPa;G为剪切模量，MPa;

裂缝中某点压裂液的压力pf可由裂缝内压裂液压降[13]计算得到:

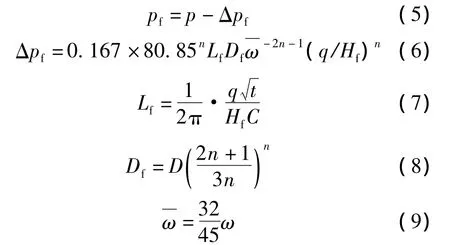
式中:p为井底压裂施工压力，MPa;Δpf为压裂液压降，MPa;q为排量，m3/min;C为综合滤失系数;t为施工时间，min;D为压裂液稠度系数，Pa·sn;n为压裂液流态指数;Df为幂律液缝流稠度系数，Pa·sn;Lf为裂缝总长，m为平均裂缝宽度，cm。

压裂裂缝的宽度受到裂缝内压裂液的压力控制，随着压裂裂缝的延伸，压裂液的压力逐渐减小，压裂裂缝宽度也相应减小。

2.2 裂缝走向计算

为了减少模糊参数的应用并简化计算模型，设定当压裂裂缝和天然裂缝的夹角θ为30°～150°时(图1中θ1)，裂缝会沿着天然裂缝方向向两侧延伸，整条天然裂缝都会被开启;当压裂裂缝和天然裂缝的夹角θ小于30°或者大于150°时(图1中θ2)，裂缝只能沿着天然裂缝的一个方向延伸，当压裂液延伸到天然裂缝尽头时，压裂裂缝会继续沿着最大水平主应力方向延伸。

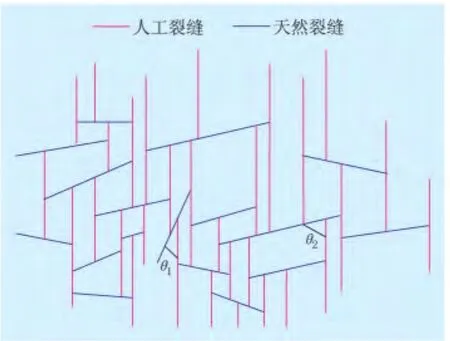
图1 裂缝延伸形态示意图

裂缝延伸的范围受裂缝总长度约束，而裂缝总长度受压裂液总量和压裂时的延伸压力控制。根据压裂液总量守恒原理，总的裂缝体积应该等于总的压裂液体积减掉地层滤失的压裂液体积(不考虑压裂液体积系数)，根据裂缝的宽度、高度和压裂裂缝体积即可得到压裂裂缝的总长度，以此来约束压裂裂缝的延伸长度。随着压裂裂缝的延伸，裂缝中会存在压降，距井越远压力损失越大，当压裂液压力低于延伸压力时，地层不能再被压开，裂缝也随即停止延伸。

3 压裂缝网沟通效果评价设计

压裂裂缝沟通效果评价参数设计包括2个部分:基础参数指标。主要包括预压裂储层体积ERV、有效压裂体积FRV、增产储层体积SRV、平均裂缝孔隙度φf和总裂缝体积Vf;沟通评价指标。

为了能更深入地评价人工裂缝与天然裂缝的沟通情况，设计了3个方面的6个指标。

3.1 与储层整体沟通效果指标

把水平井水平段储层区域作为一个整体对象，用以下2个指标来评价压裂裂缝在储层中的压裂范围，评价压裂缝网在储层中的波及范围。

(1)裂缝网络体积百分数，即有效压裂体积与预压裂储层体积百分比:

式中:FCR为裂缝网络体积百分数，%;FRV为有效压裂体积，m3;ERV为预压裂储层体积，m3。

(2)裂缝体密度增长率，即裂缝网络中裂缝体密度增加值与压裂前裂缝体密度比值:

式中:FDR为裂缝体密度增长率，%;Ssf、Ssf0为储层所有裂缝压裂后与压裂前的单面面积，m2。

3.2 与天然裂缝沟通效果指标

人工裂缝在沟通储层的同时，也在沟通更多的天然裂缝，与天然裂缝沟通得越多，增加储层渗透性的效果越好。

(1)天然裂缝沟通程度，即水平井段平面内人工裂缝和天然裂缝接触条数与天然裂缝原有条数的比值:

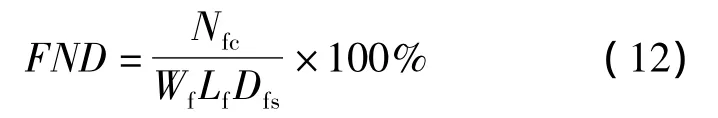
式中:FND为天然裂缝沟通程度，%;Nfc为人工裂缝与天然裂缝相交条数，即人工裂缝沟通天然裂缝条数;Wf为裂缝网络的宽度，m;Lf为距井轴的最远距离，m;Dfs为天然裂缝面密度，条/m2。

(2)天然裂缝沟通效率，即该指标为开启天然裂缝的体积与压裂裂缝体积的百分比:

式中:FNR为天然裂缝沟通效率，%;VNf为开启的天然裂缝体积，m2;Vf为压裂裂缝体积，m2。

3.3 裂缝网络通道沟通效果指标

裂缝网络已经形成，但对产能的贡献取决于通道的有效性，借助人工压裂的效果评价，引入以下指标作为评价页岩气藏的有效沟通效果。

(1)增产储层体积百分比，即有效压裂体积中增产储层体积所占比例:

式中:SFR为增产储层体积百分比，%;SRV为增产储层体积，即有效压裂体积中具有人工裂缝或者人工裂缝沟通天然裂缝的网格块累计储层体积，m3;FRV为有效压裂体积，m3。

(2)裂缝网络的导流能力，即平均裂缝宽度乘以平均裂缝渗透率，用以描述裂缝的渗流能力:

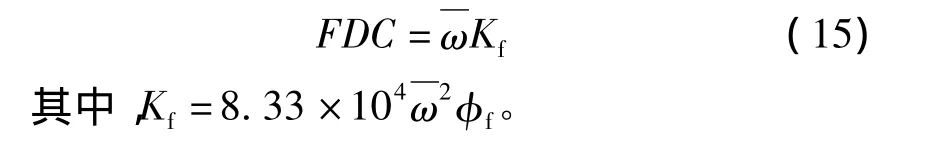
式中:FDC为裂缝网络的导流能力，10－3μm2·m;Kf为平均裂缝渗透率，10－3μm2。

4 验证与算例

表1～3为某页岩气藏储层缝网模拟参数，对其进行缝网模拟及沟通效果评价分析。

表1 某页岩气储层缝网储层参数

表2 某页岩气储层缝网天然裂缝参数

表3 某页岩气储层缝网压裂参数

调整天然裂缝参数和压裂相关地层参数，进行压裂缝网模拟，得到模拟的二维结果(图2)。图2中与水平井相交密集连续线区域为缝网区域，在区域外的离散线为理想天然裂缝网络。由图2可知，压裂缝网区域已经实现了人工裂缝与天然裂缝的沟通。

图2 水平井压裂缝网形态

压裂缝网模拟结果与压裂微地震监测结果进行对比(表4)显示，模拟缝网得到的基本参数指标与微地震值均很相近，有效压裂体积误差为3.9%，增产储层体积误差为9%，总裂缝体积误差为14%，有较好的一致性。

由此可知，该压裂模型具有较高的准确性，由此反演的天然裂缝参数和压裂关键约束参数可以用于生产实际。

为进一步分析天然裂缝走向对压裂的影响，算例分别模拟了天然裂缝方位角为 15、20、30、40、50、60、70°时的压裂效果，如图3所示。

表4 模拟计算和微地震结果对比

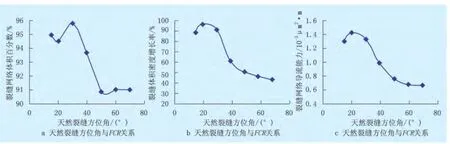
图3 裂缝网络沟通评价指标与裂缝方位角关系

由图3可知，不同天然裂缝方位角压裂形成的缝网效果也不同，方位角为20～30°时，裂缝网络体积百分数、裂缝体积密度百分数和裂缝网络导流能力均达到最大。

5 结论

(1)天然裂缝的基本参数不易获取，通过模拟结果与微地震的结果对比，可以拟合地层的理论天然裂缝分布，用以研究页岩气储层基于天然裂缝的产能规律。

(2)缝网评价指标体系中，基本参数可用来评价压裂的常规特征，基于人工压裂与储层沟通效果的评价新指标更具体的反映了压裂效果。

(3)天然裂缝与人工压裂缝网的模拟可对产能预测的影响因素进行分析，结合压裂缝网效果评价与产能计算模型进行对比，验证了通过压裂效果评价可以设计利于产能优化的压裂和生产模式。

[1]郑松青，姚志良.离散裂缝网络随机建模方法[J].石油天然气学报，2009，31(4):106 －110.

[2]郑松青，张宏方，刘中春，等.裂缝性油藏离散裂缝网络模型[J]. 大庆石油学院学报，2011，35(6):49－55.

[3]徐建永，武爱俊.页岩气发展现状及勘探前景[J].特种油气藏，2010，17(5):1 －6.

[4]王冕冕，郭肖，曹鹏，等.影响页岩气开发因素及勘探开发技术展望[J]. 特种油气藏，2010，17(6):12－17.

[5]王永辉，卢拥军，李永平，等.非常规储层压裂改造技术进展及应用[J]. 石油学报，2012，33(1):149－157.

[6]李庆辉，陈勉，金衍，等.新型压裂技术在页岩气开发中的应用[J]. 特种油气藏，2012，19(6):1－7.

[7]杨秀夫，刘希圣，陈勉，等.国内外水力压裂技术现状及发展趋势[J]. 钻采工艺，1998，21(4):21－25.

[8]张子明.水平井压裂技术发展现状[J].中外能源，2009，14(9):39 －44.

[9]叶军，曾华盛.川西须家河组泥页岩气成藏条件与勘探潜力[J].天然气工业，2008，28(12):18－25.

[10]童亨茂.储层裂缝描述与预测研究进展[J].新疆石油学院学报，2004，16(2):9 －13.

[11]Teimoori A，Chen Z，Rahman S S，et al.Calculation of permeability yensor using boundary element method provides a unique tool to simulate naturally fractured reservoirs[C].SPE84545，2003:1 －8.

[12]Weng X，Kresse O，Cohen C，et al.Modeling of hydraulic fracture network propagation in a naturally fractured formation[C].SPE140253，2011:2 －9.

[13]张琪.采油工程原理与设计[M].东营:石油大学出版社，2006:267－287.