卫星导航系统多路复用信号相关峰检测算法研究

潘伟川，王雪， 贺成艳

（1.中国科学院 国家授时中心, 西安 710600；2.中国科学院 精密导航定位与定时技术重点实验室，西安 710600；3.中国科学院大学，北京 100049）

卫星导航系统多路复用信号相关峰检测算法研究

潘伟川1，2，3，王雪1，2， 贺成艳1，2

（1.中国科学院 国家授时中心, 西安 710600；2.中国科学院 精密导航定位与定时技术重点实验室，西安 710600；3.中国科学院大学，北京 100049）

卫星导航系统多路复用信号支路信号之间的干扰导致接收信号的自相关函数不完全对称，影响了传统接收机的捕获性能。为了解决上述问题，提出了涉及两个对称相关函数的算法。通过该算法得到的接收信号自相关函数是完全对称的，且可降低其他支路信号或噪声对需要处理的信号的影响。通过仿真验证了新算法在多路复用信号捕获和抑制干扰方面的优越性。

导航信号；多路复用；信号捕获；相关函数

0　引言

随着全球卫星系统的发展和人们对定位精度需求的增加，导航卫星需要发射更多的信号，然而导航频段资源有限，导航卫星需要在同一频段发射更多信号。现代化的GPS卫星在L1频点需要同时发射L1M，C/A码和P（Y）码3路信号，在L2频点上需要同时发射P（Y），L2C和M码信号。Galileo卫星在E1和E6每个频点也要同时发射3路信号。考虑到导航卫星高功放功率有限且存在非线性失真，目前GPS和Galileo提出了运用互复用技术[1]将3路导航信号调制成具有恒包络特性的多路复用信号的方案。所以接收机接收到的GPS或Galileo导航系统的多路复用信号中将至少包含3路信号。而不同用户根据不同需求，往往仅需要其中一路信号，其他支路信号则视为干扰。

随着卫星导航系统的飞速发展，导航系统需要更多信号来满足日趋多样化的用户需求，然而有限的频率资源及卫星平台高功放有限的功率限制了卫星信号很难在多频段发射多路信号。在导航系统中，导航信号多采用码分多址技术以降低同频段信号之间的干扰。但在实际中不可能生成完全随机的码，应用中一般使用伪随机码。伪随机码长度是有限的，两个不同的伪随机码的互相关函数不是处处为0，叠加到信号的自相关函数中，会对接收信号的自相关函数产生影响。所以当接收机接收到的信号是多路复用信号时，必须考虑其他支路信号产生的互相关干扰。经过大量仿真分析验证，当多路信号中各支路信号发射功率在同一数量级时，其他支路信号对接收信号的跟踪的影响误差在毫米级。在高精度分析中，该影响虽小但不容忽视，而且不排除经过星载设备如滤波器和高功率放大器（HPA）后，误差进一步扩大的可能。同时导航信号接收通道中存在的热噪声也会对导航信号的捕获跟踪产生较大的影响。

如果接收机接收信号的自相关函数和理想信号的自相关函数越接近，那么接收机捕获跟踪误差将越小，精度越高[2-3]。然而，虽然理想信号自相关函数是对称的，但由于接收信号中既包含需要的信号也包含同频点其他支路信号和热噪声，所以现有接收机处理信号算法[4-5]得到的信号的自相关函数将是不对称的，且对多路复用信号中其他支路信号和噪声的抑制效果不理想。本文基于理想信号的自相关函数具有交换律而互相关函数不具有交换律这一性质，提出了一种新的算法，多路复用信号经过该算法得到的信号自相关函数将是对称的，而且抑制其他支路信号干扰的效果优于传统信号处理算法。根据理论分析和仿真结果可得，改进的算法相对于传统算法最高可提高接收信号载噪比3 dB-Hz。

本文通过理论和仿真验证了改进的算法得到的信号自相关函数具有对称性并且更接近理想信号的自相关函数。本文共分为4部分，其中第1部分介绍了现有接收机处理信号生成相关函数的算法并阐述了现有算法生成的相关函数不对称的原因，第2部分介绍了本文提出的算法并给出了该算法得到的相关函数具有对称性的证明，第3部分给出了现有接收机处理算法与改进算法在性能上的比较，第4部分给出了仿真验证结果。

1　现有接收机相关处理算法

本节将根据现有的接收机捕获跟踪算法经典理论，给出接收机传统算法生成的信号自相关函数，并证明传统算法生成信号的自相关函数不具有对称性。

多路复用信号在每个信号中含有多个支路信号，且每个支路信号具有不同的测距码。传统接收机接收到的多路复用信号的数学表达式为

式（1）中，s1（t）是需要处理的信号，s2（t）和s3（t）是其他支路信号，a，b，c为常数。根据现有接收机信号处理理论，接收机检测相关峰的核心算法即为接收信号与本地伪码信号作相关，数学表达式为

式（2）中，T表示预检积分时间，“*”表示共轭。由于s1（t），s2（t）和s3（t）是实信号，式（2）转化为

式（3）中，RS，s1（τ）表示接收机接收到的信号与本地复制的伪码信号的相关函数。为了便于对s1（ t）信号的自相关函数进行分析，对式（3）归一化可以得到：

式（4）中，Rs1（τ），Rs2，s1（τ）和Rs3，s1（τ）分别表示s1（ t）的自相关函数，s2（ t）和s1（ t）信号的互相关函数，s3（ t）和s1（ t）信号的互相关函数，其中Rs1（τ），Rs2，s1（τ）和Rs3，s1（τ）的数学表达式为

可以看到归一化之后传统检测相关函数算法其实包含3组互相关函数的计算。

相关峰不对称属于信号畸变的一种，相关峰不对称将最终导致伪码测距结果偏离正常值，特别是导致宽窄相关测距结果不一致。由于两个信号的互相关函数具有不对称性，所以现有接收机处理算法将导致接收信号与本地伪码的相关函数不具有对称性，并最终导致伪码测距误差。证明如下：对式（4），以-τ代换τ，就可得下式：

由于s2（ t），s1（ t），s3（ t）均表示单支路信号，为实函数，所以式（8）即为

由于一般情况下互相关函数不具有交换律，所以

比较式（1）和（9），可以得到下式：

这说明传统的相关峰检测算法得到的信号的相关函数是不具有对称性的。

2　改进的算法

2.1改进的算法

由于互相关函数不具有交换律[6]而自相关函数具有交换律，为了使得到的相关函数具有对称性，新的处理方法做了如下处理：首先使用传统算法将接收信号与本地伪码信号作互相关，得RS，s1（τ），其次将本地伪码与接收信号的共轭作相关得Rs1，S*（τ），最后将2者求和并求平均，算法的数学表达式如下所示：

将式（12）中的第2项展开得到：

由于s1（ t），s2（ t）和s3（ t）均为实函数，式（13）可转化为

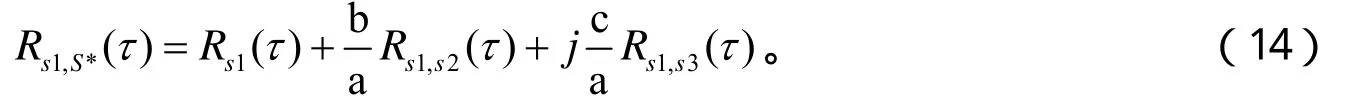
将式（4）和（14）相加可以得到：

可以看到归一化之后，该相关函数算法其实包含6组相关函数的计算。

2.2自相关函数对称性

这里的S（ t）是复信号，而s1（ t）是实信号。对式（15），以-τ取代τ可以得到：

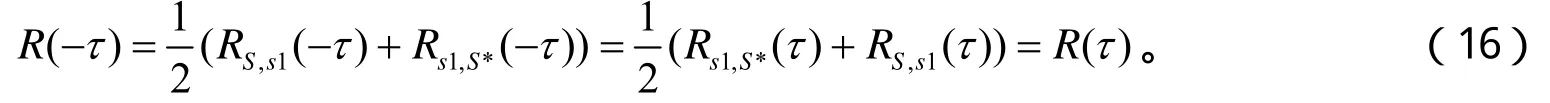
由于R（τ）=R（-τ），则该相关函数是关于中心轴对称的，即改进的算法得到的接收信号的相关函数具有对称性。

2.3相关函数的相似性分析

本节从理论上给出了改进算法接收信号的自相关函数更接近理想信号的自相关函数的原因。本节评估接收信号的相关函数与理想信号的自相关函数的相似性的指标是方差。传统信号算法得到信号的自相关函数与理想信号的自相关函数的方差即为

式（17）中，Rs1（τ）和分别表示s1（ t）的归一化自相关函数和接收信号S（ t）与s1（ t）的归一化互相关函数。式（17）表明传统算法得到的信号自相关函数的方差中包含S2和S3对S1信号的互干扰。

改进的算法得到的相关函数与需要处理的信号的自相关函数的方差可以表示为

式（18）中，R（τ）表示改进算法得到的接收信号与本地伪码信号的互相关函数。与传统算法相似，方差中包含S2和S3对S1信号的互干扰。

由于两个数的和的平方小于两个数的平方和的2倍，那么可以有下式：

同理可以得到：

将式（19）和（20）代入式（18）得：

合并同类项可得：

即经过改进算法处理得到的接收信号的相关函数方差小于传统算法得到的信号相关函数的方差，这表明改进的算法得到的信号的自相关函数与理想信号的自相关函数更接近。

3　评估方法

本节将分别给出验证改进算法得到的信号的自相关函数与理想信号的自相关函数相似度的评估方法和验证改进算法具有对称性的仿真方法。信号的相关函数的相似性与信号的谱分离系数是等效的，为了便于仿真分析，本文以两种算法得到的信号自相关函数与理想信号的自相关函数的谱分离系数为仿真指标。

3.1谱分离系数

由信号的相关理论知，信号的自相关函数的傅里叶变换即为信号的功率谱密度，两个信号的互相关函数的傅里叶变换即为2者的互功率谱密度。所以我们使用谱分离系数来表征两个算法得到的信号相关函数与信号理想相关函数的相似程度。两个不同信号的谱分离系数表征了两个不同信号的功率谱密度的差异度，其数学表达式为

式（23）中，i=1，2，3，Gs（f）为S（ t）信号的功率谱密度，Gsi（f）为si路信号的功率谱密度。由于接收信号的自相关函数傅里叶变换即为信号的功率谱密度，因此谱分离系数可以表征不同的算法得到的信号的相关函数与理想信号的自相关函数的相似性。相似性越高，谱分离系数值越大，捕获算法性能越优越。

设T=1ms，改进的算法得到的互功率谱密度IGs，si（f）为

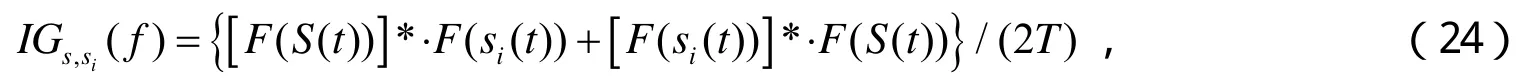
传统的算法得到信号的功率谱密度为

改进的算法得到的信号自相关函数与理想信号的自相关函数的谱分离系数Iκs，si为

传统捕获算法得到的信号自相关函数与理想信号的自相关函数的谱分离系数为

式（24）~（27）中，F（）代表傅里叶变换算法。

3.2信号相关函数的对称性

由式（16）知，改进的算法得到的信号的相关函数具有对称性，传统算法得到的信号的相关函数不具有对称性。具有对称性的自相关函数有助于提高导航信号伪码跟踪精度。本文评估相关函数的对称性的方法如下：①相关函数以中心轴翻转并相减得差值G（τ）-G（-τ）；②取差值的绝对值，并进行积分③观察积分值的大小，积分值越大，相关函数的对称性越差。

4　仿真分析

Interplex复用技术是一种相位调制技术，复用信号具有恒包络特性。由于该复用技术具有操作简单、复用效率较高等优点而引起了导航信号研究者的广泛关注。本节仿真GPS导航系统L1频段的M码信号，L1Cd信号和L1Cp信号，其调制方式分别为BOC（10，5），BOC（1，1）和TMBOC（6，1，4/33）。根据ICD-GPS-200显示的L1Cd和L1Cp信号地面最低接收功率，将上述3信号的功率归一化得L1Cd、L1Cp和M码信号的归一化功率分别为0，6.02，4.7 dBW[7-8]。根据Interplex复用技术复用效率最大化原理，功率最大的信号需要与其他支路信号相位正交，可以得到运用Interplex复用技术复合成的复合信号，其数学表达式为

4.1信号的谱分离系数

导航信号谱分离系数反映了两个信号的相似度，谱分离系数越高，表明2者的相似度越小。图1，2和3分别给出了TMBOC（6，1，4/33），BOC（1，1）和BOC（10，5）信号的谱分离系数。通过图1，2和3可以看出改进的捕获算法得到的信号与理想信号的谱分离系数更高，这表示改进算法得到的信号功率谱与理想信号的功率谱更接近，得到的相关函数与理想信号的相关函数更相似。其中TMBOC（6，1，4/33），BOC（1，1）,BOC（10，5）信号的传统算法取得的谱分离系数与改进算法得到的谱分离系数之比分别为：0.964 3，0.959 0，0.952 7，改进的捕获算法得到的信号的相关函数更接近理想信号的自相关函数。

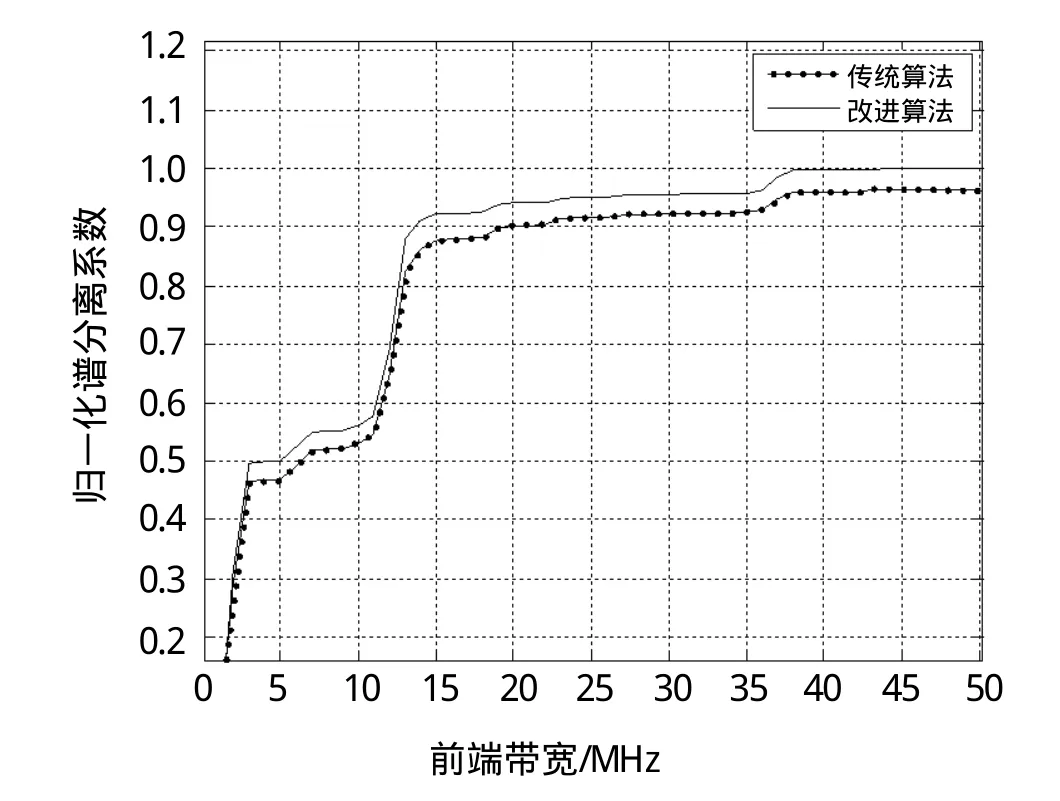
图1　TMBOC（6，1，4/33）信号谱分离系数

图2　BOC（1，1）信号谱分离系数

图3　BOC（10，5）信号谱分离系数

4.2信号自相关函数的对称性

图4，5，6和7分别给出了传统算法和改进算法得到的支路信号的自相关函数。由图4，5和6可知，改进的相关峰检测算法得到的信号自相关函数的对称性明显优于传统算法得到的信号自相关函数的对称性。由图7可知，由于BOC（10，5）信号的抗干扰特性较好，改进的捕获算法在相关函数对称性方面具有的优势不太明显。对3个调制方式的信号仿真计算得到改进算法和传统算法的信号相关函数主峰值点两边的对称点对应的相关函数值之间的差值绝对值的积分值，改进算法的积分值与传统算法的积分值之比均在10-5数量级，这说明改进算法得到的信号的相关函数的对称性更好。

图4　TMBOC（6，1，4/33）信号相关函数

图5　TMBOC（6，1，4/33）信号相关函数细节

图6　BOC（1，1）信号相关函数

图7　BOC（10，5）信号相关函数

4.3 信号相关函数的主峰值与次峰值之比

接收机捕获导航信号一般以信号自相关函数的最高峰功率电平与次高峰功率电平的比值来判断是否捕获成功，若比值大于门限值则表明捕获成功，否则未捕获成功。相关函数的峰值与次峰值的比值越大，接收机越容易捕获导航信号。表1给出了3种信号在仿真条件下的主峰功率电平与次峰功率电平的比值。由表1可知，BOC（1，1），TMBOC（6，1，4/33），BOC（10，5）信号的主峰/次峰比值分别提高了2.2，1.3，0.8 dB，这表明改进算法抑制其他支路信号和热噪声干扰的效果要优于传统算法，这将使得接收机更容易捕获信号。

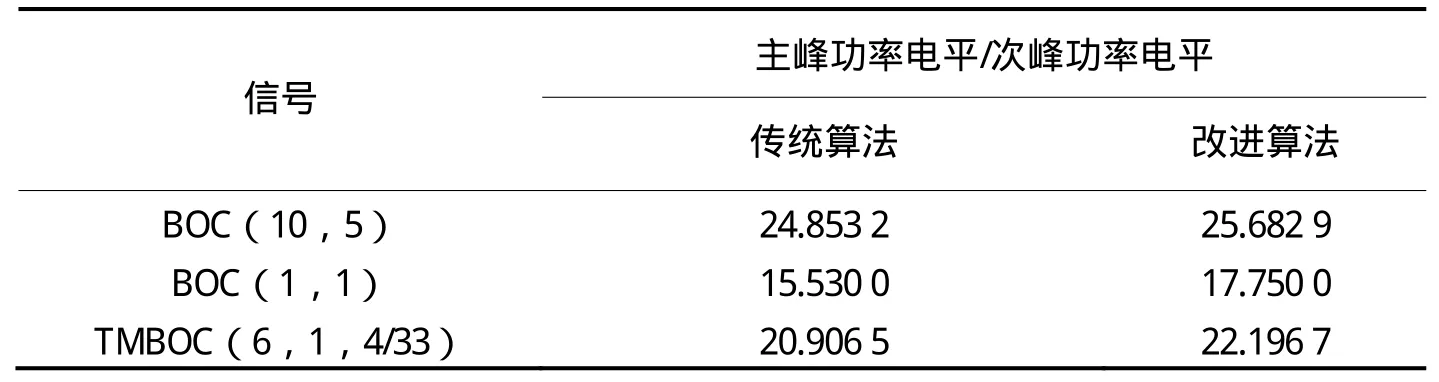
表1　信号相关函数的主峰功率电平/次峰功率电平 dB

5　总结

由以上分析可见：①改进算法得到的信号自相关函数比传统算法得到的信号的相关函数更逼近于理想信号的自相关函数，而且该算法得到的相关函数是完全对称的；②改进算法改善了信号的信噪比和信号自相关函数的主峰值与次峰值之比，而这更有利于导航信号的捕获。

本文的研究成果可以为导航系统多路复用信号接收机和抗干扰接收机的设计提供有价值的参考。

[1]BUTMAN S, TIMOR U.Interplex-an efficient multi-channel PSK/PM telemetry system[J].IEEE Transaction on Communications, 1972, 20(3): 415-419.

[2]BETZ J W, KOLODZIEJSKI K.Generalized theory of code tracking with an early-late discriminator part I: lower bound and coherent processing[J].IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(4): 1538-1556.

[3]BETZ J W, KOLODZIEJSKI K.Generalized theory of code tracking with an early-late discriminator part II: noncoherent processing and numerical results[J].IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(4): 1557-1564.

[4]卡普兰, 赫加蒂.GPS原理与应用[M].2版.寇艳红, 译.北京: 电子工业出版社, 2007: 163-172.

[5]谢钢.GPS原理与接收机设计[M].北京: 电子工业出版社, 2012: 267-344.

[6]郑君里, 杨为理.信号与系统[M].北京: 高等教育出版社, 2010: 341-349.

[7]BETZ J W.The offset carrier modulation for GPS modernization[C]// Proceedings of the 1999 National Technical Meeting of The Institute of Navigation.San Diego, CA: Proceedings of the Institute of Navigation's National Technical Meeting, 1999, 1: 639-648.

[8]BETZ J W.Design and performance of code tracking for the GPS M code signal[C]// Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation.Proceedings of the Institute of Navigation's National Technical Meeting, 2000.

Research on correlation peaks detection algorithm for multiplex signal of navigation systems

PAN Wei-chuan1，2，3， WANG Xue1，2， HE Cheng-yan1，2
（1.National Time Service Center， Chinese Academy of Sciences， Xi'an， 710600， China；2.Key laboratory of Precision Navigation， Positioning and Timing Technology， National Time Service Center，Chinese Academy of Sciences， Xi'an， 710600， China；3.University of Chinese Academy of Sciences， Beijing 100049， China）

The interference among the tributary signals of the same multiplex signal of the satellite navigation system results in the unsymmetrical autocorrelation function， and influences the receiver's capturing performance.In order to solve the above problems， a new algorithm involving a pair of symmetrical correlation function is presented.The new algorithm is able to get completely symmetrical autocorrelation function and reduce the influence of the noise and the interference from the other tributary signals.The superiority of the method in capturing the multiplexed signal and suppressing the interference is proved through simulation.

navigation signals； multiplex； signal acquisition； correlation function

TN96

A

1674-0637（2015）03-0163-08

10.13875/j.issn.1674-0637.2015-03-0163-08

2014-10-20

国家自然科学基金委员会重点资助项目（11073022）；中国科学院西部博士专项资助项目（2013BS25）；卫星导航与定位教育部重点实验室（B类）开发基金课题。

潘伟川，男，硕士，主要从事导航多路复用信号检测、捕获和跟踪，多路复用方式评估的研究。