压裂裂缝网络不稳态流动半解析模型

贾 品，程林松，黄世军，李 权

（中国石油大学石油工程学院，北京102249）

压裂裂缝网络不稳态流动半解析模型

贾 品，程林松，黄世军，李 权

（中国石油大学石油工程学院，北京102249）

与压裂单条缝及多条缝的流动模式不同，包含相互交错裂缝的压裂裂缝网络流动会在裂缝交汇处产生流向重定向和流量重分配的过程。通过引入星三角变换法，并结合有限差分方法对这一特殊流动过程进行描述，推导裂缝网络内部流动数值解。基于Laplace空间源函数及叠加原理建立油藏流动解析解。耦合该两部分流动，给出一个压裂裂缝网络不稳态流动半解析模型，并利用现场实例验证模型的实用性。结果表明：该模型可以处理裂缝空间位置和导流能力任意分布的裂缝网络，能够预测生产井的压力、产量动态及不同生产阶段的油藏压力分布；在上下封闭无界储层中，压裂缝网存在裂缝内部线性流、裂缝与地层双线性流、地层线性流、过渡流以及拟径向流；受井筒存储效应的影响，观测不到裂缝内部线性流；渗透率为1×10-7μm2级别的储层在生产早、中期流体流动主要集中在密度大及导流能力高的裂缝附近，但最终（生产30～50 a）的泄流区域都局限在压裂改造范围内，改造区外的储层流体很少流动。

压裂裂缝网络；星三角变换法；有限差分；点源函数；瞬态响应

利用水力压裂技术有效开发低渗透油藏已有多年历史。近年来，应用于非常规油藏，如致密油藏及页岩气藏开发的水平井分段压裂丰富了已有的压裂技术，相关的压裂缝渗流理论也成为了学者们研究的热点。国内外学者Gringarten［1］、Cinco-Ley［2］、张义堂［3］、Schulte［4］等均利用源函数等方法研究了压裂直井单条裂缝无限导流及有限导流下的不稳态流动过程。Guo和Evans［5］采用实空间源函数和Newmann乘积法得到了有多条压裂缝的水平井不稳态流动解析解。Raghavan［6］、Chen［7］、姚军［8］、王晓冬［9］等基于Ozkan［10］给出的Laplace空间源函数，并结合势叠加原理推导了多条横向压裂水平井不稳态流动半解析解。以上方法明确了压裂单条或多条缝的不稳态流动特征，并对压后产能评价、地层及裂缝参数反演提供了坚实的理论基础。对于岩石脆性系数高且天然裂缝发育的储层，生产井经体积压裂后，通常会在近井地带形成压裂裂缝网络［11-12］。由于人工压裂缝和天然缝空间位置上复杂交错，裂缝网络内部流动不再局限于单条缝或多条缝内常见的线性流，而是在裂缝相交处还存在流向重定向和流量重分配的交汇流动。同时，各裂缝导流能力的不同使交汇流动更为复杂。对其不稳态流动进行建模时，以上方法［1-9］的应用就受到了一定的限制。对于压裂裂缝网络流动，国内外学者在解析解和半解析解上研究很少，主要以数值模拟方法为主。Al-Ahmadi［13］假设人工裂缝和天然裂缝相正交，且等间距分布，通过耦合三个线性流模型推导了产量及压力动态解析解。Zhou［14］规定了裂缝交汇处的流动方向，利用源函数和叠加原理得到缝网流动半解析解。袁彬［15］、蔡田田［16］、Mayerhofer［17］和Cipolla［18］等均利用数值模拟方法研究了正交裂缝网络的产能。现场中，缝网内的裂缝往往成角度相交，假设裂缝正交局限性较大；同时流体在裂缝交汇处的流向及流量应由相交裂缝之间的传导率和压力自动决定，人为规定流动方向将使计算结果产生一定的误差。目前关于压裂裂缝网络流动仍然缺少一种准确的、适用性强的数学模型。笔者通过耦合裂缝和油藏流动建立一个准确预测缝网不稳态流动的半解析模型，利用该模型计算不同压裂缝的生产动态，划分地层流体的流动阶段，分析油藏压力分布特征，并进行实例研究。

1　物理模型

在均质上下封闭无界油藏中，一口水平井经压裂后在近井地带形成如图1（a）所示的非正交裂缝网络。地层、裂缝及流体均微可压缩，且压缩系数为常数。单相流体在地层和裂缝中的流动服从不稳定Darcy渗流。其中，水平井只在与裂缝相交处射孔，其他段均封闭。不考虑重力的影响，同时假设裂缝垂直并贯穿储层，则流体在油藏中的流动为二维问题。

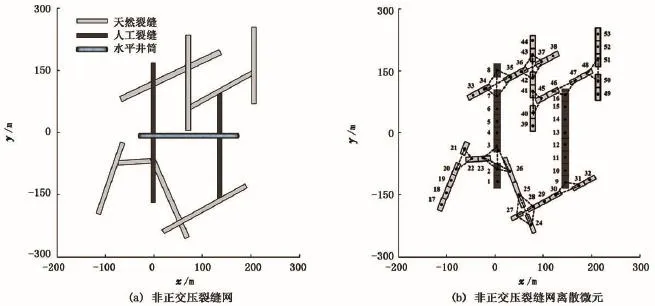
图1　非正交压裂缝分布及离散裂缝微元示意图Fig.1 Schematics of un-orthogonal complex hydraulic fracture geometry and segments

如图1（b）所示，将该裂缝网络离散为NS=53个微元，并顺序编号，每个裂缝微元可以有不同长度和导流能力。地层流体在每个裂缝微元上均匀分布，但每个裂缝微元的地层流量和压力均不同。

2　数学模型

假设地层流体为单相黑油。生产井正常生产时，地层流体先从油藏流向裂缝，再由裂缝流向生产井筒，最后流向地面。若认为井筒内管流摩阻可以忽略，即井筒无限导流，则以上流动可分为油藏流动和裂缝内部流动，分别对这两种流动过程进行建模，再在裂缝面进行压力和流量耦合，建立压裂裂缝网络不稳态流动半解析模型。为了统一和简便，将各变量变换成无因次变量进行相关计算和研究。定义无因次参数如下：

式中，k为油藏渗透率，μm2；φ为油藏孔隙度；h为油藏厚度，m；pi为原始地层压力，MPa；μ为地层流体黏度，mPa·s；B为地层流体体积系数；ct为综合压缩系数，MPa-1；qw为井的产量，m3/d；t为时间，h；pfi为裂缝微元i的压力，MPa；qfi为油藏流向裂缝微元i的流量，m3/d；（xfi，yfi）为裂缝微元i的几何中心，m；ΔLfi裂缝微元i的长度，m；kfwf为裂缝微元i的导流能力，μm2·cm；φfi为裂缝微元i的孔隙度；cfti为裂缝微元的压缩系数，MPa-1；ε为裂缝方向；LF为参考长度，m；下标w表示生产井；下标f表示裂缝，下标i表示裂缝微元索引，下标D代表无因次。值得注意的是，本文中虽以油藏为研究对象，但对于气体流动，只须引入拟压力函数，其余无因次变量与油藏相同。

2.1油藏流动

基于Laplace空间源函数求得油藏流动解析解。Ozkan［10］给出了Laplace空间中不同边界条件下的点源函数。油藏流体向裂缝流动时，相当于NS个裂缝微元同时生产。基于势叠加原理，将多个裂缝微元同时生产产生的干扰由源函数的叠加实现。第i个裂缝微元的压力卷积公式为

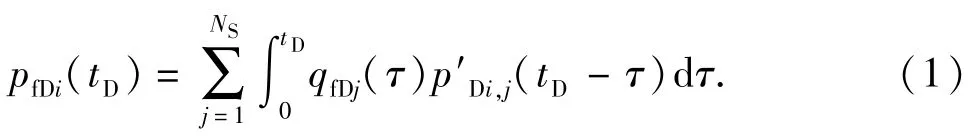
对式（1）进行Laplace变换，

将式（2）应用到所有裂缝微元，得到包含NS个等式的矩阵方程为

其中

式中，s为Laplace变量；K0为零阶第二类修正贝塞尔函数；f（s）为双重孔隙介质中的窜流函数，对于本文中的单孔介质f（s）=s；θ为裂缝微元与x轴的夹角。

2.2裂缝内部流动

压裂形成人工裂缝的宽度通常为毫米级别，相对整个油藏尺寸，其宽度可忽略。即在二维油藏流动中，裂缝流动可认为呈一维流动。对于压裂裂缝网络，流动不再局限于一维线性流，而是在裂缝相交处存在交汇流动。存在交汇流动的裂缝微元数在总裂缝微元数中所占比例不大。笔者建模思路为：在裂缝空间位置不变的前提下，给出暂不考虑裂缝交汇流动的拟缝网流动，然后利用星三角变换法对相对少量的相交裂缝微元流动方程进行变换，修正之前得到的拟缝网流动方程，进而得到真实的缝网流动等式。

实空间下裂缝内不稳态流动方程的无因次形式为

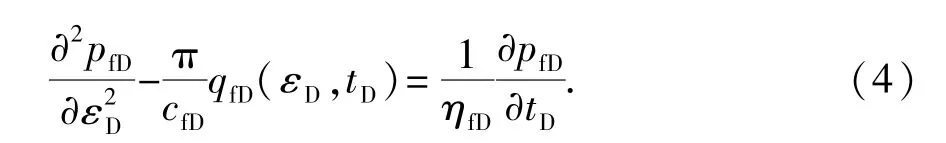
假设油藏初始时刻压力分布均匀，裂缝端部封闭，生产井定产量生产，则初始条件及内外边界条件为

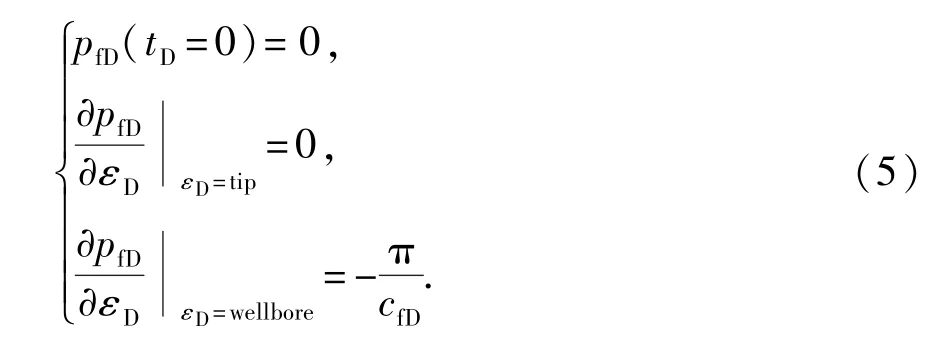
其中，tip表示裂缝端部，wellbore表示与井筒相连。将式（4）和（5）分别进行Laplace变换后如下：

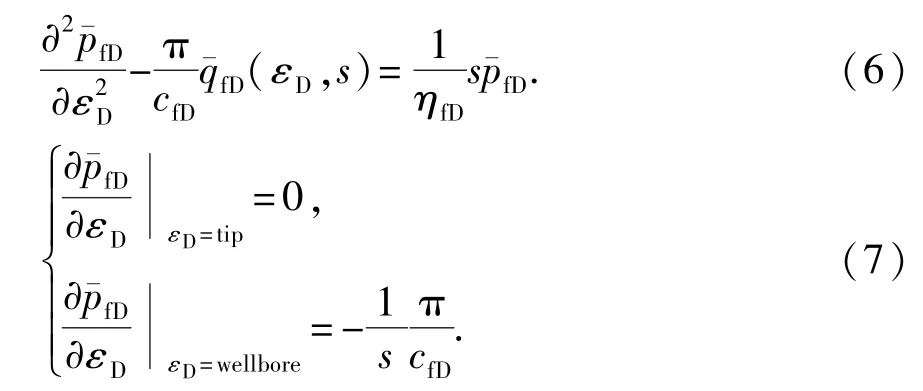
将式（6）在裂缝微元上离散，得到以下有限差分形式：

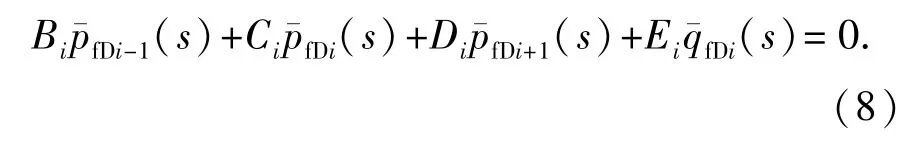
式中，Bi、Ci、Di和Ei为系数。

式（7）中的定产边界条件的离散形式为

基于压力和流量在裂缝面的连续性，式（3）和（8）中的压力和流量相同。联立式（3）、（8）和（9），给出不考虑裂缝交汇流动下压裂井定产量生产时的压力动态方程。

2.3裂缝交汇流动

交汇流动只存在于相交裂缝处，如图1中编号为2、9和48的裂缝微元。图2给出了裂缝相交的几种情况。以图2（c）为例，标号为1～4的为裂缝微元，标号0表示交汇单元。在裂缝内部流动方程中，须引入交汇单元及其压力值确定地层流体在交汇处的流动方向与流量分配；在油藏流动中，交汇单元相对于裂缝微元体积太小，不能作为源汇项，即不能引入到油藏流动方程中。在耦合油藏和裂缝流动时，类似于标号0的交汇单元就成了奇异单元。该类奇异单元将会导致油藏流动矩阵方程和裂缝流动矩阵方程秩的不同而无法耦合，必须设法消去。

首先，考虑图2（c）中相邻两个单元之间的流动，以交汇单元0和裂缝微元2为例，流动表达式为

其中

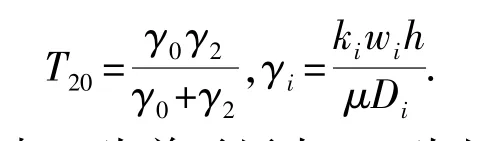
式中，p为单元压力；Q20为从单元2到单元0的流量；kiwi为单元i的导流能力；Di为单元i几何中心到连接界面中心的距离。

图2　裂缝微元相交示意图Fig.2 Schematics of fracture segments intersecting

考虑到交汇单元的尺寸相对于裂缝微元的尺寸非常小D2≫D0，并假定交汇单元与相邻的裂缝微元有相近的导流能力k2w2k0w0，因此有γ2≪γ0，则两单元之间的传导率近似为

同理，对裂缝微元1、3和4分别有T40γ4、T10γ1和T30γ3。

为消去人工裂缝与天然裂缝之间的交汇单元，应用电路网络中电流与多孔介质中渗流相似原理。图3说明了电路网络的星三角变换法。King［19］首次利用该方法计算了非均质油藏中储层有效渗透率。Karimi［20］将其应用到离散裂缝网络（DFN）流动模拟中，消除了由于裂缝交汇形成的控制体积。利用图3的变换过程消去交汇单元0，使1～4裂缝微元直接相邻，则地层流体在裂缝交汇处的流向重定向和流量重分配就可直接通过裂缝微元的压力和传导率自动决定。Karimi［20］指出变换后相邻裂缝微元之间的传导率计算式为

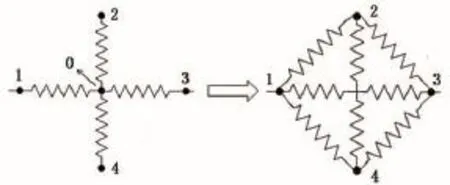
图3　星三角变换法示意图Fig.3 Schematics of star-delta transformation

2.4不稳态流动过程求解

压裂井的生产动态通过联立油藏流动式（3）和经星三角变换法修正得到的裂缝流动式（8）并结合边界条件（9）得到。从以上3个表达式可以看出，求解任何一个等式都需要其他两个等式中的未知量，因此压力动态的计算是3个等式相互耦合的过程。本文中利用类似Al-Kobaisi［21］的耦合方法，以如图4所示的简单压裂缝网说明耦合求解过程。标号为1～4表示人工裂缝微元，标号5～8为天然裂缝微元。耦合计算矩阵为

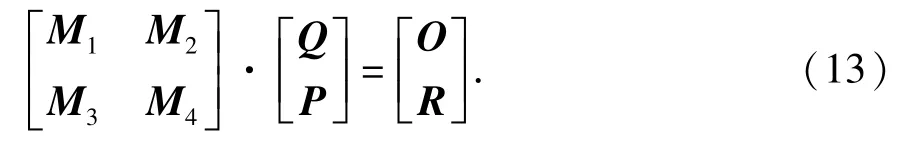
根据式（3），有M1=A8×8，M2=-I［］0，I为8× 8的单位矩阵，O为8×1的全0向量。其余的矩阵和向量为

图4　简单缝网示意图Fig.4 Schematics of simple hydraulic fracture network

由于受到缝网内外边界条件及交汇流动的影响，处于不同位置的裂缝微元其流动式（8）会有所不同，即对应的压力和流量项的系数会发生变化。以下对裂缝微元分类讨论，并给出以上耦合矩阵中各系数的计算式。

（1）内部裂缝微元。根据式（8），该类微元的离散控制方程为

式（14）的系数为

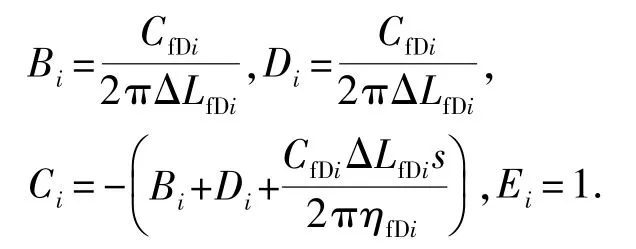
（2）交汇裂缝微元。标号为2、3、6和7均为交汇裂缝微元。以微元2为例，其在拟缝网流动中的式（8）经星三角变换后为

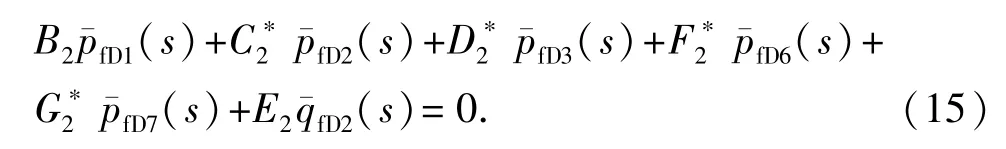
利用式（12）推导得式（15）的系数为

对编号为3、6、7的裂缝微元进行类似以上的变换，完成从拟缝网流动到真实缝网流动的转换。

（3）与井筒相邻的裂缝微元。对于与井筒直接相邻的裂缝微元（i=1），式（8）变为

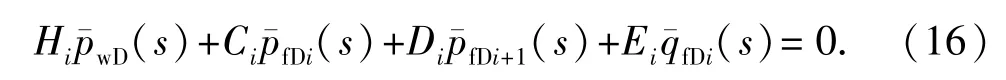
其中

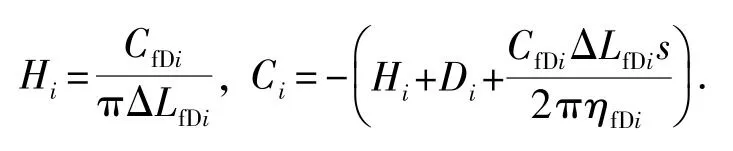
矩阵M4中的其余Hi（i≠1）均为0。

（4）封闭边界处裂缝微元。对于处于封闭边界的裂缝微元（i=4，5，8），式（8）中没有Bi或Di。

（5）定产内边界条件。压裂井定产量生产时式（10）写成如下离散形式：

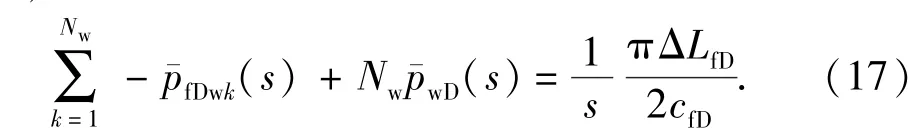
其中，压力项的系数和右端常数分别对应矩阵M4中的Li和Ri，L1=-1，L9=Nw，其余Li均为0；R9=其余Ri均为0。

Everdingen和Hurst［22］指出，在Laplace空间中将wD带入以下等式可以考虑井筒存储效应和表皮系数的影响，

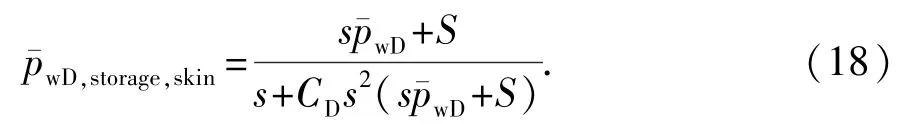
式中，S为表皮系数；CD为无因次井筒存储系数（CD=C/（2πφcthL2F））。

定压生产下的无因次产量表达式为

求解矩阵（13），并利用Stehfest数值方法［23］反演式（18）和（19），可得实空间下的压力和产量动态。将式（3）应用到油藏不同位置时，可以计算不同时刻油藏的压力分布。最后需要注意的是：由于式（4）采用一维流动对缝内流动进行建模，因此对于垂直于压裂水平井的横切缝，还须引入聚流表皮因子Sc［24］，并利用类似于式（18）的方法再次修正井底压力，表达式为

3　不同形态裂缝的不稳态流动过程

虽然本文中提出的半解析模型主要针对压裂裂缝网络，但由于对裂缝内流动采用数值解，因此该模型同样适用于简单压裂缝。为验证模型的准确性和通用性，分别对压裂单条缝、多条缝、正交缝网以及非正交缝网的生产动态进行预测，并与文献［2］及文献［8］的经典结果进行对比。

3.1单条裂缝井底压力动态

假设直井钻完井后进行水力压裂，形成两侧等长度的双翼缝，裂缝完全穿透储层。利用半解析模型预测其井底压力动态，并与已有结果对比。设参考长度LF为裂缝半长，无因次裂缝导流能力为cfD=40，无因次裂缝导压系数为ηfD=1.0×10-6。图5为不考虑井筒存储效应和表皮系数的无因次井底压力以及压力导数对比曲线。从结果中可以看出，在整个生产时间段内，本文中模型与文献［2］结果吻合度很高。生产中也出现了较明显的流动形态：①早期裂缝与地层双线性流（压力与压力导数呈斜率1/4直线）；②早期地层线性流（压力与压力导数呈斜率1/2直线）；③中期过渡流；④晚期拟径向流（压力导数为0.5）。

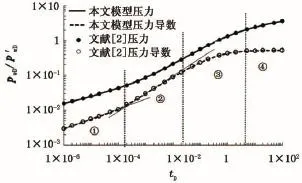
图5　本文模型与文献［2］模型单条裂缝压力动态对比曲线Fig.5 Comparison of pressure and derivative responses of this model and reference 2 model for single fracture

3.2多条裂缝井底压力动态

新钻水平井分4段压裂，压裂设计人工缝等间距分布，各裂缝半长与导流能力均相等。利用本文模型预测其压力动态，并与前人计算结果对比。其中取参考长度LF为裂缝半长，cfD=40，ηfD=1.0×10-6，相邻裂缝间距为LF的5倍，对比结果如图6所示。从图6的对比结果中看出，本文的压力及压力导数与文献［8］的计算结果吻合很好。同时也反映了多段压裂水平井压力动态曲线的基本特征，流动方式的顺序是：①早期双线性流动（压力与压力导数为斜率1/4直线）；②早期地层线性流动（压力与压力导数为斜率1/2直线）；③中期径向流动（压力导数为0.5/4= 0.125）；④双径向流动（压力导数为斜率0.36直线）；⑤晚期拟径向流动（压力导数为0.5）。

3.3非正交裂缝网络生产动态

现场体积改造所形成的缝网中，裂缝常成不同角度复杂交错。以图1（c）所示的裂缝网络为例，计算其压力及压力导数，划分其流动形态。同时求解不同时刻储层不同位置的压力值，预测油藏压力分布。计算非正交裂缝网络生产动态基本参数：油藏厚度为70 m，油藏渗透率为1×10-7μm2，油藏孔隙度为0.05，油藏初始压力为20 MPa，综合压缩系数为1.4×10-4MPa-1，地层流体黏度为0.8 mPa·s，人工裂缝导流能力为20 μm2·cm，人工裂缝孔隙度为0.46，人工裂缝压缩系数为1.2×10-4MPa-1，天然裂缝导流能力为5 μm2·cm，天然裂缝孔隙度为0.54，天然裂缝压缩系数为1.1×10-4MPa-1，产量为0.7 m3/d，表皮系数为0，无因次井筒存储系数为0。

图7为非正交缝网的压力及压力导数动态曲线。由动态曲线可以得出，缝网的流态过程可分为5个阶段：①早期裂缝内部线性流，即油藏流体未流动，只有裂缝内部流体流动，这一流动过程与Cinco -Ley［25］文中的解析式（8）相似，由于处理单缝或多缝有限导流时通常假设裂缝内为稳态流动，加之裂缝总长度较小，因此很难观测到裂缝内部线性流，本文中对裂缝流动采用不稳态建模，同时整个缝网裂缝总长度较大，因此裂缝线性流较明显；②早期裂缝与地层双线性流，类似于单缝和多缝的双线性流，该流动由裂缝内部线性流和油藏线性流组成，压力以及压力导数呈斜率为1/4的直线，此时裂缝之间还未出现压力干扰；③早期地层线性流，压力以及压力导数呈斜率为1/2的直线，油藏流体以垂直于距其最近的裂缝流动；④中期过渡流，从压力场看，裂缝之间压力干扰明显，生产所需的流体大部分来自于缝网内部储层；⑤晚期拟径向流，缝网外部地层流体开始流动，此时压力波以近似于圆形向外传播，压力导数为0.5的直线。

图8为对应生产阶段的油藏压力场。图8直观地反映出压力降首先产生在小间距和高导流能力裂缝的附近储层，然后向外扩展。压裂井的正常生产主要通过裂缝网络内部油藏降压保证。即使生产50 a，油藏衰竭区域也仅限在经压裂改造的储层中，改造区外的储层流体很少流动。由此可见，增大裂缝网络体积、降低裂缝间距、提高裂缝导流能力是开发渗透率在1×10-7μm2级别储层的一种有效措施。

图8　非正交缝网不同生产阶段裂缝及附近地层压力分布Fig.8 Pressure distribution of un-orthogonal fracture network for different prodcution periods

3.4正交裂缝网络生产动态

虽然将裂缝网络假设为正交缝网过于理想，但从内容的完整性讲，研究正交缝网的生产动态也有一定必要性。由于正交缝网关于水平井筒对称，以缝网的一半（图9）为例，其中人工缝半长120 m，共3条；天然缝长180 m，共5条。无因次井筒存储系数CD=1×10-4，表皮系数S=0.01，其余参数同上。

如图10所示的压力及压力动态曲线，考虑井筒存储效应和表皮系数影响后，井筒续流段（图10中流动阶段①）掩盖了早期裂缝内部线性流。其余流动阶段皆与图8中的流动段②～⑤类似。图11为缝网不同生产时间的油藏压力分布特征，也与非正交缝网相似。

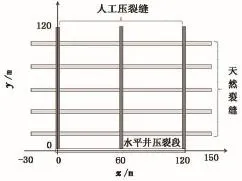
图9　正交裂缝网络示意图Fig.9 Schematics of orthogonal hydraulic fracture network

图10　正交裂缝网络压力及压力导数曲线Fig.10 Transient pressure and derivative of orthogonal hydraulic fracture network

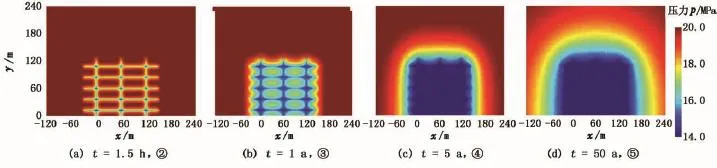
图11　正交缝网不同生产时间裂缝及附近地层压力分布Fig.11 Pressure distribution of orthogonal fracture network for different prodcution periods

4　实例应用

本文模型的实例应用须明确压裂裂缝网络空间位置及导流能力分布。国内关于该方面的文献较少，国外研究较多。以Barnett页岩区一口分段多簇压裂水平井W1为例［26］，应用本文模型预测其生产动态。

W1井分4段压裂，压后对第1段进行了详细的微地震监测，地层及流体参数也较为全面。文献［26］结合监测结果和裂缝扩展模型得到了裂缝空间位置及导流能力分布，如图12（a）所示。本文实例所用的缝网如图12（b）所示。其中，基质渗透率为1×10-7μm2，油藏、人工裂缝及天然裂缝的孔隙度分别为0.13、0.47和0.53，油藏厚度为140 m，初始压力为27.6 MPa，井底流压为8.6 MPa，其余参数可参见文献［26］。图13为气体PVT高压物性。值得注意的是，以下计算中并未考虑页岩气体的扩散、滑脱及解析吸附过程，目的是把重点落在复杂压裂缝网流动的处理上。相对于油藏流动，气藏流动只须引入拟压力函数即可。裂段的无因次井底压力，再利用式（19）以及Stehfest数值反演方法计算无因次产量，最后将无因次产量因次化，得到日产气量及累积产气量曲线，结果如图14所示。图15为不同生产时间下裂缝及油藏压力分布。可以看出在生产早、中期，气藏流动主要集中在裂缝间距小（即裂缝密度大）和裂缝导流能力高的附近储层；同时从生产30 a的压力场可以看出，气藏最终泄流区域均局限在压裂改造的储层范围内。

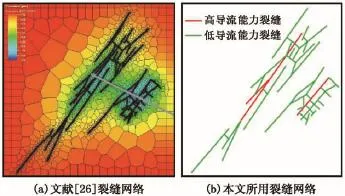
图12　文献［26］及本文实例所用的复杂压裂缝网Fig.12 Complex hydraulic fracture network from reference 26 and used for field example in this paper

图13　储层条件下的气体高压物性Fig.13 Gas properties at reservoir conditions

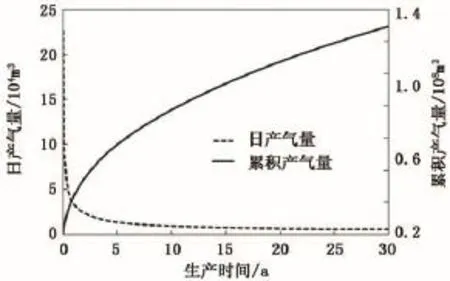
图14　第1压裂段的产气速度和累积产气量Fig.14 Gas rate and cumulative gas production profile in stage one

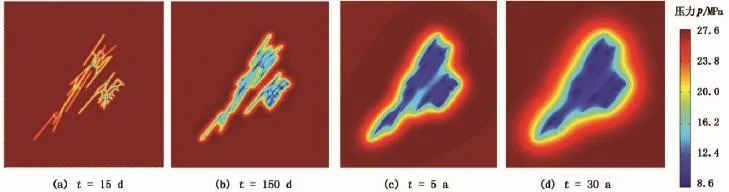
图15　W1井第1压裂段不同生产时间裂缝及附近地层压力分布Fig.15 Pressure distribution of stage one of well W1 for different prodcution periods

5　结 论

（1）结合星三角变换法和有限差分方法解决了相交裂缝间的交汇流动问题。通过耦合油藏流动解析解和裂缝内部流动数值解，得到了压裂裂缝网络不稳态流动半解析模型。该模型适用于裂缝空间位置和导流能力任意分布的裂缝网络，可以计算生产井的产量和压力动态，同时可以预测不同生产时刻储层的压力分布。

（2）在上下封闭无界储层中，压裂缝网存在裂缝内部线性流、裂缝与地层双线性流、地层线性流、过渡流以及拟径向流。受井筒存储效应的影响，观测不到裂缝内部线性流。渗透率为1×10-7μm2级别的储层在生产早、中期流体流动主要集中在密度大及导流能力高的裂缝附近；但最终（生产30～50 a）的泄流区域都局限在压裂改造范围内，改造区外的储层流体很少流动。

（3）Barnett页岩区一口分段多簇压裂水平井实例验证了本文模型的实用性。

［1］ GRINGARTEN A C，RAMEY H J.The use of source and green's functions in solving unsteady flow problems in reservoirs［R］.SPE 3818，1973.

［2］ CINCO LEY H，SAMANEIGO V F，DOMINGUEZ N. Transient pressure behavior for a well with a finite-conductivity vertical fracture［R］.SPE 6014，1978.

［3］ 张义堂，刘慈群.垂直裂缝井椭圆流模型近似解的进一步研究［J］.石油学报，1996，17（4）：71-77. ZHANG Yitang，LIU Ciqun.Further study on the approximate solutions of the elliptical flow model for wells with vertical fractures［J］.Acta Petrolei Sinica，1996，17（4）：71-77.

［4］ SCHULTE W M.Production from a fractured well with well inflow limited to part of the fracture height［R］. SPE 12882，1996.

［5］ GUO G L，EVANS R D.Pressure-transient behavior and inflow performance of horizontal wells intersecting discrete fracture［R］.SPE 26446，1993.

［6］ RAGHAVAN R，CHEN C C，AGARWAL B.An analysis of horizontal wells intercepted by multiple fractures［R］.SPE 27652，1997.

［7］ CHEN C C，RAGHAVAN R.A multiply-fractured horizontal well in a rectangular drainage region［R］.SPE 37072，1997.

［8］ 姚军，刘丕养，吴明录.裂缝性油气藏压裂水平井试井分析［J］.中国石油大学学报：自然科学版，2013，37（5）：107-119. YAO Jun，LIU Piyang，WU Minglu.Well test analysis of fractured horizontal well in fractured reservoir［J］.Journal of China University of Petroleum（Edition of Natural Science），2013，37（5）：107-119.

［9］ 王晓冬，罗万静，侯晓春，等.矩形油藏多段压裂水平井不稳态压力分析［J］.石油勘探与开发，2014，41（1）：74-78. WANG Xiaodong，LUO Wanjing，HOU Xiaochun，et al. Transient pressure analysis of multiple-fractured horizontal wells in boxed reservoirs［J］.Petroleum Exploration and Development，2014，41（1）：74-78.

［10］ OZKAN E，RAGHAVAN R.New solutions for well-testanalysis problems：part I-analytical consideration［R］. SPE 23593，1991.

［11］ FISHER M K，HEINZE J R，HARRIS C D，et al.Optimizing horizontal completion techniques in the barnett shale using microseismic fracture mapping［R］.SPE 90051，2004.

［12］ XU W，THIERCELIN M，GANGULY U，et al.Wiremesh：a novel shale fracturing simulator［R］.SPE 132218，2010.

［13］ AL-AHMADI H A，WATTENBARGER R A.Triple-porosity models：one further step towards capturing fractured reservoirs heterogeneity［R］.SPE 149054，2011.

［14］ ZHOU W，BANERJEE R，POE B，et al.Semi-analyti-cal production simulation of complex hydraulic fracture networks［R］.SPE 157367，2012.

［15］ 袁彬，苏玉亮，丰子泰，等.体积压裂水平井缝网渗流特征与产能分布研究［J］.深圳大学学报：理工版，2013，30（5）：545-550. YUAN Bin，SU Yuliang，FENG Zitai，et al.Productivity distribution and flow characteristics of volume-fractured horizontal wells［J］.Journal of Shenzhen University（Science and Engineering），2013，30（5）：545-550.

［16］ 蔡田田.低渗透油藏体积压裂数值模拟研究［D］.大庆：东北石油大学石油工程学院，2013. CAI Tiantian.Study on the volume fracturing numerical simulation in low-permeability reservoir［D］.Daqing：College of Petroleum Engineering in Northeast Petroleum University，2013.

［17］ MAYERHOFER M J，LOLON E P，YOUNGBLOOD J E，et al.Integration of microseismic fracture mapping results with numerical fracture network production modeling in the barnett shale［R］.SPE 102103，2006.

［18］ CIPOLLA C L.Modeling production and eveluating fracture performance in unconventional gas reservoirs［R］. SPE 118536，2009.

［19］ KING P R.The use of renormalization for calculating effective permeability［J］.Transport in Porous Media，1989，4（1）：37-58.

［20］ KARIMI-FARD M，DURLOFSKY L J，AZIZ K.An efficient discrete fracture model applicable for general purpose reservoir simulators［R］.SPE 79699，2003.

［21］ AL-KOBAISI M，OZKAN E，KAZEMI H.A hybrid numerical/analytical model of a finite-conductivity vertical fracture intercepted by a horizontal well［R］.SPE 92040，2006.

［22］ van EVERDINGEN A F，HUST W.The application of the laplace tranformation flow problems in reservoirs［J］.Journal of Petroleum Technology，1949，1（12）：305-327.

［23］ STEHFEST H.Numerical inversion of laplace tranform［J］.Communications of Acm，1970，13（1）：47-49.

［24］ MUKHERJEE H，ECONOMIDES M J.A parametric comparison of horizontal and vertical well performance［R］.SPE 18303，1991.

［25］ CINCO LEY H，SAMANIEGO V F.Transient pressure analysis for fractured wells［R］.SPE 7490，1981.

［26］ CIPOLLA C L，FITZPATRICK T，WILLIAMS M J，et al.Seismic-to-simulation for unconventional reservoir development［R］.SPE 146876，2011.

（编辑 李志芬）

A semi-analytical model for transient flow behavior of hydraulic fracture networks

JIA Pin，CHENG Linsong，HUANG Shijun，LI Quan
（College of Petroleum Engineering in China University of Petroleum，Beijing 102249，China）

Comparing with the flow in single and multiple fractures，the flow behaviors in hydraulic fractured networks that consist of interconnected fractures are featured of flow redirection and flux redistibution at fracture intersections.In this paper，the flow behavior in fractured networks was modeled and the numerical solution was given by combining star-delta transformation and finite difference methods.An analytical solution for the flow in reservoir matrix was obtained based on source functions in Laplace domain and superposition principles.A semi-analytical model for the transient flow in hydraulic fractured networks was derived by dynamically coupling these two flow processes.The model was verified with a field case study.The results show that the semi-analytical model can be applied to fracture networks with arbitrary geometry and variable fracture conductivity.The transient bottomhole pressure and production rate can be solved along with reservoir pressure distribution during different production periods.In an infinite slabed reservoir，the flow in hydraulic fractured networks can be classified into five flow regimes，including the fracture linear flow，bilinear flow，formation linear flow，transient flow and pseudo-radial flow.The afterflow caused by wellbore storage effect may overshadow the fracture linear flow.For the reservoirs with permeability of 1×10-7μm2，the fluid drainage occurs primarily in the vicinity of the fractures with large density and higher conductivity at the earlymiddle production periods.However，the ultimate depletion（e.g.after 30-50 years of production）is still limited to the region of the stimulated reservoir volume and the fluid flow beyond the stimulated region makes little contribution to the total produc-tion.

hydraulic fracture networks；star-delta transformation；finite difference method；point source function；transient responses

TE 312

A

1673-5005（2015）05-0107-10

10.3969/j.issn.1673-5005.2015.05.015

2015-01-09

国家自然科学基金项目（51174215，E0403）

贾品（1990-），男，博士研究生，研究方向为油藏工程和渗流理论。E-mail：jiapin1990@163.com。

引用格式：贾品，程林松，黄世军，等.压裂裂缝网络不稳态流动半解析模型［J］.中国石油大学学报：自然科学版，2015，39（5）：107-116.

JIA Pin，CHENG Linsong，HUANG Shijun，et al.A semi-analytical model for transient flow behavior of hydraulic fracture networks［J］.Journal of China University of Petroleum（Edition of Natural Science），2015，39（5）：107-116.