钻井地质参数的不确定性表征及分析方法

魏 凯，管志川，马金山，齐金涛，胜亚楠

（1.中国石油渤海钻探钻井技术服务公司，天津300280；2.中国石油大学石油工程学院，山东青岛266580）

钻井地质参数的不确定性表征及分析方法

魏 凯1，2，管志川2，马金山1，齐金涛1，胜亚楠2

（1.中国石油渤海钻探钻井技术服务公司，天津300280；2.中国石油大学石油工程学院，山东青岛266580）

钻井地质参数是钻井工程设计的基础数据，由于地层的复杂性、预测模型的精度以及解释资料的误差等问题，地质参数的解释评价结果误差客观存在，其真值会分布于某区域内。首先提出钻井地质参数不确定性的概率分布和不确定度两种描述方法；然后基于层序地层学、概率统计等相关理论和方法，将同组地层内某段地层作为样本区间，区间内的地质参数作为一组测量样本，建立地质参数不确定性分析及量化描述方法，并基于信息扩散原理确定钻井地质参数的概率分布函数。实例分析表明，建立的钻井地质参数不确定性定量描述及分析结果更切合工程实际。

钻井；地质参数；不确定性；概率分布；信息扩散；地层孔隙压力

钻井地质参数是反映岩体环境综合性质的基础数据，对钻井工程设计、监测及规避钻井风险具有重要意义。由于油气地质的复杂性、解释资料的不完备性以及数学模型的精度等问题，无法获得地质参数真值，其误差客观存在，所得地质参数具有不同程度的分散性或不确定性，真值会以一定概率形式分布于某区间内。目前，在实际钻井工程中，多利用地震或井筒资料［1］解释地质参数，并用确定性的单一数值对其加以描述，对工程不确定性因素的考虑主要采用经验性设计、区域性统计分析或安全系数［2-5］，主观性强，缺乏理论意义。笔者基于层序地层学、概率统计等相关理论和方法，将同组地层内某段地层作为样本区间，区间内的地质参数作为一组测量样本，建立地质参数不确定性分析及量化描述方法，使钻井地质参数的定量描述更切合工程实际。

1　钻井地质参数不确定性表征

由于不确定性的存在，钻井地质参数真值会分布于某区域内［4-8］，具有分散性。分散程度反映了测量结果在某种程度上的可信度。目前，处理不确定性的方法主要有随机模型方法、模糊模型方法和区间分析方法。根据不确定性的处理方法，地质参数真值的不确定性可用参数的概率分布或不确定度（不确定性区间）描述。

（1）概率分布形式。概率理论使用概率分布描述随机变量的不确定性。如果具有足够的信息能够确定常规统计分析的基本概率分布，可以用概率分布对不确定性进行描述。

（2）不确定度形式。不确定度是指因为测量时存在误差，对真值不能肯定的程度。不确定度包括余量（区间）I和置信概率P，表示被测量值落在区间I的可能性为P。不确定度描述了真值可能落在的区间。

在统计信息不足以描述钻井地质参数不确定的概率分布、只能根据先验知识获得其区间时，运用不确定度对钻井地质参数的不确定性进行描述具有其特殊优势。例如检测到某地层的地层孔隙压力为（1.15±0.15）g/cm3，有95%的置信概率。检测结果说明该地层的地层孔隙压力为（1～1.3）g/cm3的可能性为95%。

2　地质参数不确定性分析

2.1基本原理

油气田年代地层单位划分为界、系、统、群、组、段等级次。地层划分是根据地质、地震、测井、分析化验等资料以及构造、地层层序等有关信息，在纵向上研究不同层段地层的时序变化，分析地层间的差异性及其组合特征，认识它们各自的特性。界、系、统、群、组、段对应的纵向单元和尺度不同，前者较大、粗糙，后者较小、精细，因此在油气田中，岩性特征分析、地层横向对比或油藏精细描述等许多油气工程领域的问题基本是以组、段为基础单元进行研究的。理论和实践证明［9-12］，在同一地质时期、同样的沉积条件下应产生同样或相近的岩性、地震或测井响应。同一时期沉积的地层具有相同或相近的地质、地震、测井等参数的响应区间；不同时期沉积的地层，具有不同的参数变化区间，这也是地层组划分对比的基础和依据。测点间的距离越小，测井响应结果越具有相似性。基于该思想，将同组地层内相邻测点间的测井解释地质参数作为一组测量样本，确定每个测点处的钻井地质参数不确定性概率分布或区间。

2.2不确定性分析方法

（1）假设条件。假设某井的钻井地质参数为X，在井深区间ΔH=［Hu，Hl］内共有（2n+1）个离散值，如图1所示。由于地层的空间连续性，该参数在ΔH区间内具有相似性和连续性，可以将区间ΔH内的钻井地质参数作为数据点i所处井深处地质参数的一个测量样本｛x（i-n），x（i-n+1），…，x（i+n）｝，并称ΔH为样本区间。

图1　样本示意图Fig.1 Schematic diagram of sample

（2）样本区间的确定。考虑到地质参数空间变异性限制，样本区间ΔH不宜过大，可以参考该地层组内的变异函数计算得到的变程［13］确定。假设待分析地层组内不同深度hk（k=1，2，…，N）处的地质参数为P（hk），深度间隔为Δh，则变异函数为

对不同的深度间隔mΔh（m=1，2，…，N-1），可计算相应的γ（mΔh），然后选取相应的理论变异函数对离散点［mΔh，γ（mΔh）］（m=1，2，…，N-1）进行拟合，确定理论模型参数，把两倍的变程（模型参数之一）作为样本区间ΔH。

（3）概率分布函数确定。若μ（ξ）为区间ΔH=［Hu，Hl］上的一个波雷尔函数，可以得到i处的钻井地质参数X的一个概率密度函数估计为

式中，C为窗宽，常数，且C＞0。

基于分子扩散理论，可以确定波雷尔函数μ（ξ）的显示正态表达式为

则钻井地质参数X在区间ΔH=［Hu，Hl］上的正态信息扩散概率密度函数为

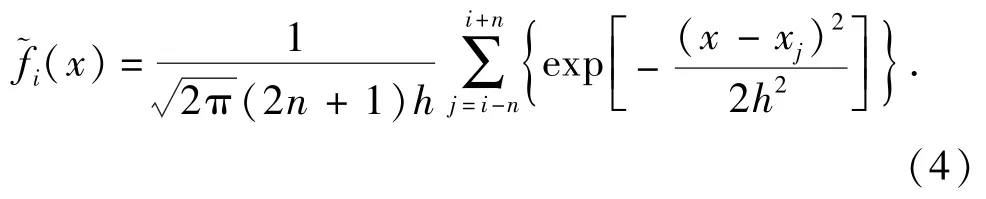
式中，h=Cσ，为扩散系数。

假设钻井地质参数X在区间ΔH=［Hu，Hl］内的最大值为xmax，最小值为xmin，扩散系数计算式为

系数λ由表1确定。

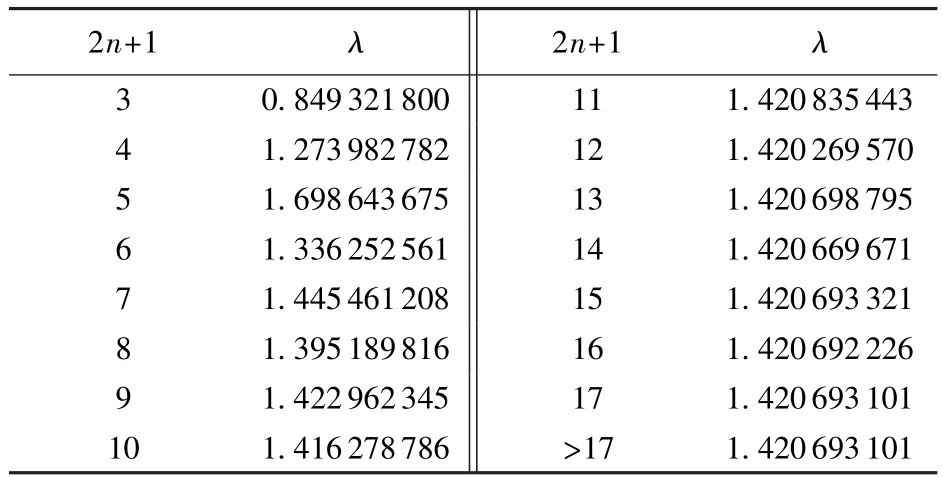
表1　λ值与样本数2n+1的对应关系Table 1 Relationship between λ and 2n+1

（4）概率分布的拟合优度检验。K-S单样本检验主要用来检验一组样本数据的实际分布是否与某一指定的理论分布相符合［14-15］。用Fn（x）表示样本量为n的随机样本观察值的累积分布函数，且Fn，n（i是小于等于x的所有样本数目），F（x）表示理论分布的累积概率分布函数。K-S单样本检验通过样本的累积分布函数Fn（x）和理论分布函数F（x）的比较做拟合优度检验。检验统计量是F（x）与Fn（x）间的最大偏差Dn：

当实际观测Dn＜D（n，α）（D（n，α）是显著水平为α、样本容量为n时的临界值，表2）时，认为实际样本分布函数与理论分布函数的拟合程度很高。

（5）钻井地质参数的不确定性区间。考虑小概率事件不易发生的特性［16］，以一定的可信度获取钻井地质参数的分布区间［kl，ku］，可以得到对测量点i处不确定性的度量（以地层孔隙压力为例，图2）：①分布区间［kil，kiu］；②区间内的概率分布函数估计fi（x）。

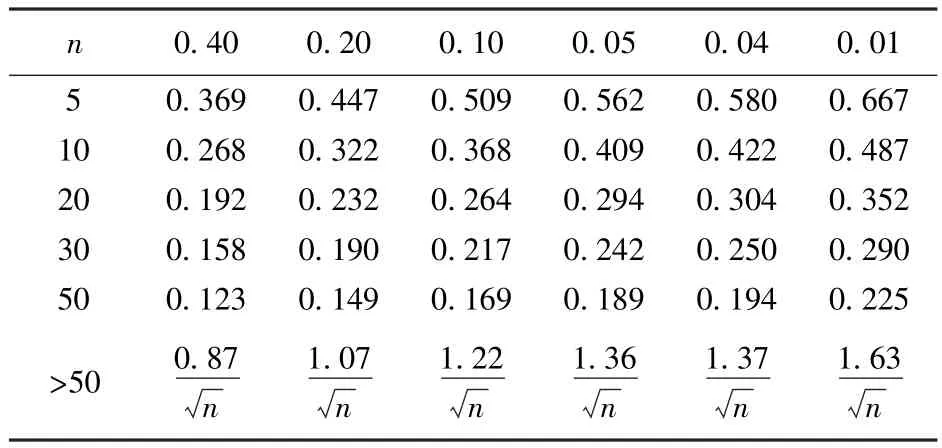
表2　D（n，α）Table 2 Reference list of D（n，α）

对所有点进行同样处理，获得全井地质参数的不确定性信息。

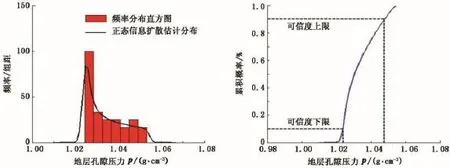
图2　某深度处地质参数不确定性分析示意图Fig.2 Uncertainty analysis diagram of geological feature parameter

3　算 例

W井是西部某油田一口重点勘探井，测井资料及其地质分层如图3所示。利用Eaton法计算该井地层孔隙压力，利用本文中的理论方法对地层孔隙压力的不确定性进行分析，并与现场压力测试进行对比。

地层孔隙压力不确定性分析时，通过变异函数计算确定样本区间为8 m，可信度上、下限累积概率分别为10%和90%，分析结果如图4所示。通过对比分析可以看出，地层孔隙压力实测值包含在具有不确定性信息的地层孔隙压力区间内，不确定性分析结果能够真实反映地质参数的可信度及其分布区间。

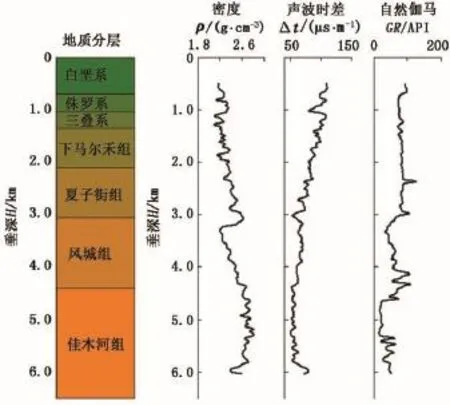
图3　地质分层及测井曲线Fig.3 Geological stratification and logging curves

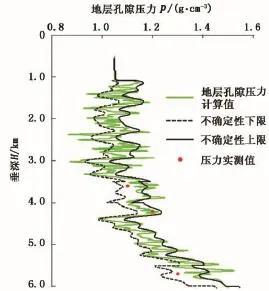
图4　地层孔隙压力概率分布区间Fig.4 Probability distribution interval of formation pore pressure

4　结 论

（1）由于不确定性的存在，钻井地质参数真值会分布于某区域内，具有分散性，分散性程度反映了测量结果在某种程度上的可信度。提出了地质参数不确定性的概率分布和不确定度两种描述方法。

（2）在同一地质时期、同样的沉积条件下产生的地层具有相同或相近的岩性特征，在该地层内地质、地震、测井响应亦相同或相近。将同组地层内某小区间作为样本区间，样本区间内的测井解释地质特征参数作为一组测量样本，基于概率分布的相关理论，建立了钻井地质特征参数不确定性的分析方法。

（3）受钻井工程实际限制，可确定钻井地质参数的样本较少，因此直接测量须选用小样本概率分布计算方法。工程实际中，受诸多因素影响，样本可能不严格服从标准分布函数，或难以估计其理论概率分布的参数。小样本情况下，基于信息扩散估计确定的概率分布更加接近参数的真实分布。

［1］ 管志川，魏凯.利用已钻井资料构建区域地层压力剖面的方法［J］.中国石油大学学报：自然科学版，2013，37（5）：71-75. GUAN Zhichuan，WEI Kai.A new method for establishing regional formation pressure profile based on drilled wells data［J］.Journal of China University of Petroleum（Edition of Natural Science），2013，37（5）：71-75.

［2］ 魏凯，管志川，廖华林，等.井壁失稳风险评价方法［J］.中国石油大学学报：自然科学版，2013，37（2）：62-66. WEI Kai，GUAN Zhichuan，LIAO Hualin，et al.Assessment method of borehole instability risk［J］.Journal of China University of Petroleum（Edition of Natural Science），2013，37（2）：62-66.

［3］ 管志川，魏凯，傅盛林，等.基于区间分析的钻井工程风险评价方法［J］.石油钻探技术，2013，41（4）：15-18. GUAN Zhichuan，WEI Kai，FU Shenglin，et al.Risk evaluation method for drilling engineering based on interval analysis［J］.Petroleum Drilling Techniques，2013，41（4）：15-18.

［4］ 窦玉玲.深水钻井钻井液密度窗口及套管层次确定方法研究［D］.东营：中国石油大学石油工学学院，2006. DOU Yuling.Research on the drilling fluid density window and casing layers design in deep water［D］.Dongying：School of Petroleum Engineering in China University of Petroleum，2006.

［5］ 柯珂.深水钻井套管层次及下入深度确定方法研究［D］.东营：中国石油大学石油工程学院，2009. KE Ke.Casing program design method for deepwaterdrilling［D］.Dongying：School of Petroleum Engineering in China University of Petroleum，2009.

［6］ 茆诗松，程依明，濮晓龙.概率论与数理统计教程［M］.北京：高等教育出版社，2004.

［7］ 张建国，陈建军，马孝松，等.不确定结构动力特征值区间分析的一种算法［J］.应用力学学报，2006，23（1）：96-100. ZHANG Jianguo，CHEN Jianjun，MA Xiaosong，et al. Method for dynamic values interval analysis of uncertain structures［J］.Chinese Journal of Applied Mechanics，2006，23（1）：96-100.

［8］ 林洪桦.测量误差与不确定度评估［M］.北京：机械工业出版社，2010.

［9］ 石玉章，杨文杰，钱峥.地质学基础［M］.东营：石油大学出版社，2004.

［10］ CATUNEANU O.层序地层学原理［M］.吴因业，译.北京：石油工业出版社，2009.

［11］ SANSTROM W C，HAWKINS M J.Perceiving drilling learning through visualization［R］.IADC/SPE 62759，2000.

［12］ 李黎，王永刚.地质统计学应用综述［J］.勘探地球物理进展，2006，29（3）：163-169. LI Li，WANG Yonggang.Summary of the geo-statistics application［J］.Progress in Exploration Geophysics，2006，29（3）：163-169.

［13］ 侯景儒，尹镇南，李维明，等.实用地质统计学［M］.北京：地质出版社，1998.

［14］ 宫凤强，李夕兵，邓建.小样本岩土参数概率分布的正态信息扩散法推断［J］.岩土力学与工程学报，2006，25（12）：2559-2564. GONG Fengqiang，LI Xibing，DENG Jian.Probability distribution of small samples of geotechnical parameters using normal information spread method［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（12）：2559-2564.

［15］ 熊文林，李胡生.岩石样本力学参数值的随机—模糊处理方法［J］.岩土工程学报，1992，14（6）：101-108. XIONG Wenlin，LI Husheng.A random-fuzzy method for treating the experiment of data of mechanical parameters of rock sample［J］.Chinese Journal of Rock Engineering，1992，14（6）：101-108.

［16］ 刘世君，徐卫亚，王红春.不确定性岩石力学参数的区间反分析［J］.岩石力学与工程学报，2004，23（6）：885-888. LIU Shijun，XU Weiya，WANG Hongchun.Interval back analysis on uncertain parameter in rock mechanics［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（6）：885-888.

（编辑 李志芬）

Assessment method for uncertainty of geological parameters in well drilling

WEI Kai1，2，GUAN Zhichuan2，MA Jinshan1，QI Jintao1，SHENG Yanan2
（1.Bohai Sea Oil Drilling Technology Service Company，PetroChina，Tianjin 300280，China；2.School of Petroleum Engineering in China University of Petroleum，Qingdao 266580，China）

The geological features of the rock formation to be drilling in terms of drillability and safety are very important for the drilling engineering design.The description and evaluation of the actual geological parameters are difficult due to the complexity of petroleum geology，the incompleteness of the data obtained and the lack of accuracy of the mathematical models that can be used.In fact，the geo-data obtained should be within a particular region around their actual values.In this paper，the assessment methods to describe the uncertainties of the geological parameters in terms of drilling were presented，including the probability distribution and the uncertainty description.The uncertainty analysis and their quantitative description of the geological parameters were conducted based on principles of probability，statistics and stratigraph，in which the geo-parameters were identified and classified in the same groups based on different stratigraphic formations as sample intervals.Then the probability distribution function of the drilling geological parameters was determined based on the information diffusion theory.The methods can make the quantitative description of the drilling geological parameters more relevant to the practical engineering conditions.

drilling；geological parameters；uncertainty；probability distribution；information diffusion；formation pore pressure

TE 21

A

1673-5005（2015）05-0089-05

10.3969/j.issn.1673-5005.2015.05.012

2014-12-02

国家“973”计划项目（2010CB226706）；“十二五”国家科技重大专项（2011ZX05021-001）；渤海钻探工程公司“十二五”重点培育项目（2012ZD04K）

魏凯（1983-），男，博士，研究方向为钻井工程风险监控、欠平衡钻井技术。E-mail：upcweikai@163.com。

引用格式：魏凯，管志川，马金山，等.钻井地质参数的不确定性表征及分析方法［J］.中国石油大学学报：自然科学版，2015，39（5）：89-93.

WEI Kai，GUAN Zhichuan，MA Jinshan，et al.Assessment method for uncertainty of geological parameters in well drilling［J］.Journal of China University of Petroleum（Edition of Natural Science），2015，39（5）：89-93.