定向钻井PDC钻头三维钻速预测方法

邹德永，王家骏，卢 明，陈修平，于金平

（1.中国石油大学石油工程学院，山东青岛266580；2.辽宁石油化工大学石油工程学院，辽宁抚顺113001；（3.中国石油集团西部钻探工程有限公司钻井工程技术研究院，新疆克拉玛依834000）

定向钻井PDC钻头三维钻速预测方法

邹德永1，王家骏2，卢 明3，陈修平1，于金平1

（1.中国石油大学石油工程学院，山东青岛266580；2.辽宁石油化工大学石油工程学院，辽宁抚顺113001；（3.中国石油集团西部钻探工程有限公司钻井工程技术研究院，新疆克拉玛依834000）

综合考虑PDC钻头的切削作用、钻具组合的力学作用和地层岩石可钻性各向异性，根据钻头力平衡原理，建立一种新的PDC钻头三维钻速预测方法。在钻头瞬态力平衡计算中，不仅考虑钻具组合的力学作用，还考虑钻头冠部的侧向不平衡力和保径受力对PDC钻头切削作用的影响。结果表明：井眼轨迹的预测结果与实测结果有较高的吻合度，说明方法合理；根据具体的钻头结构参数和地层可钻性各向异性，通过数值计算可获得钻头的轴向和侧向钻速，不需要取得地层法向钻进效率；在钻头瞬态力平衡计算中，钻头侧向不平衡力过大将增大井眼轨迹控制的难度，对PDC钻头布齿参数的进行优化设计可以减小钻头的侧向不平衡力，进而减小钻头漂移角和工具面变化范围，增强井眼轨迹控制能力。

钻井；PDC钻头；可钻性各向异性；井眼轨迹；钻速；定向钻井

在现有的定向钻井三维钻速预测模型中都要用到地层法向钻进效率（Dp［1］，c［2］，k［3］，Da［4］）这一关键参数，它是钻头在地层法向的钻速与受力之比，不仅与地层岩性有关，而且与钻头结构密切相关。由于PDC钻头的种类繁多，设计变化多样，很难通过现场钻井数据或室内钻进试验确定其地层法向钻进效率，这限制了模型在现场的推广应用，给井眼轨迹的预测和控制带来困难。Simon和Menand等［5-6］建立了PDC钻头钻速预测计算方法，但是不够准确详细，有待改进。笔者建立一种新的PDC钻头三维钻速预测方法，并编制定向钻井PDC钻头三维钻速预测软件，根据具体的钻头结构参数和地层可钻性各向异性，通过数值计算获得钻头的轴向和侧向钻速，而不须取得地层法向钻进效率。

1　PDC钻头三维钻速预测方法

建立的PDC钻头三维钻速预测方法是一种数值计算方法，根据钻头瞬态力平衡原理迭代反算出钻头钻速。在钻头旋转过程中，钻头旋转角度Φ每隔1°计算一次钻头的瞬时受力情况。计算步骤如下：

（1）根据切削齿的切削参数与钻头中心的位移之间的关系模型，输入给定钻头的布齿参数，并且对钻头中心的轴向位移ha和侧向位移hl赋值，可以计算出各切削齿的切削参数。具体算法见文献［7］。

（2）根据地层、井眼和钻头的坐标关系和切削齿作用力方向上的岩石可钻性级值的计算方法，输入地层参数、井眼轨迹参数和钻头参数，可以计算出各切削齿作用力方向上的岩石可钻性级值Kd。

（3）根据切削齿受力与切削参数、岩石可钻性之间的关系式，可以计算出各切削齿的正压力Fn和切削力Fc，见文献［8］。

（4）根据钻头受力计算方法可以计算出钻头冠部的轴向力Fa和侧向力Flc。

（5）令钻头中心的轴向位移ha不变，侧向位移hl=0，根据上述方法可以计算出钻头的侧向不平衡力Flb，见文献［9］。

（6）根据加权余量法，输入钻具组合参数、井眼轨迹参数和钻压W，可以计算出钻头受到的侧向力Fl。根据钻头冠部与保径在钻头侧向力中所占比例，可以计算出钻头冠部的侧向力Fla，见文献［10］。

（7）如果Fa=W，Flc=Fla+Flb，则对钻头中心的轴向位移ha和侧向位移hl所赋值是正确值，可以输出并保存该值。如果该方程不成立，则须重新对轴向位移ha和侧向位移hl赋值，直到该方程成立为止。

（8）根据以上在钻头旋转一周过程中钻头旋转角度Φ每隔1°计算出的轴向位移ha和侧向位移hl，可以计算出钻头的轴向钻速va和侧向钻速vl。

（9）根据钻头钻速与井眼轨迹的关系模型可以计算出井眼轨迹预测值。

根据上述PDC钻头三维钻速预测方法，使用Visual Basic语言编写定向钻井PDC钻头三维钻速预测软件。

2　可钻性级值的计算方法

尹宏锦［11］假设横观各向同性地层的可钻性级值在空间内呈椭球体分布，椭球的长轴为平行于岩石层面方向的可钻性级值Kdh，短轴为垂直于层面方向的可钻性级值Kdv。钻头钻进方向上的可钻性级值是该方向矢量与椭球面交点到原点的距离。根据文献［12］的地层可钻性级值预测方法，输入声波、密度和伽马测井资料，可以计算出Kdh和Kdv。

研究发现，PDC切削齿法向角不同则对应的岩石可钻性级值不同。为了确定切削齿力方向上可钻性级值需要确定切削齿与钻头、井眼、地层之间的坐标关系。

如图1所示，建立5个坐标系描述切削齿与钻头、井眼和地层之间的坐标关系。

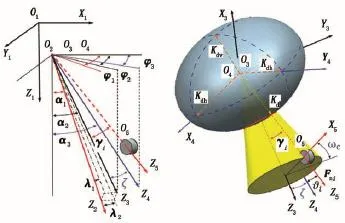
图1　切削齿与钻头、井眼、地层的坐标关系Fig.1 Coordinate relations between cutters and bit，wellbore and formation

（1）大地坐标系O1X1Y1Z1。以井口为原点O1，建立大地坐标系O1X1Y1Z1，O1X1轴指向正北，O1Z1轴指向地心。

（2）井眼坐标系O2X2Y2Z2。以井眼轴线在井底的切线为Z2轴，以井底高边为O2X2轴，建立井眼坐标系O2X2Y2Z2，原点O2在大地坐标系中垂深为D，水平位移为S，井斜角为α1，井斜方位角为φ1。

（3）钻头坐标系O3X3Y3Z3。以钻头中心O3为原点，钻头轴线为Z3轴，以钻头基准线为O3X3轴，建立钻头坐标系O3X3Y3Z3。钻头轴线Z3与Z1轴的夹角为α2，钻头轴线Z3在水平面的投影与X1轴的夹角为φ2。根据纵横弯曲连续梁法可得：钻头轴线Z3在变井斜平面的投影与Z2轴的夹角为偏转角λ1，Z3在变方位平面内的投影与Z2轴的夹角为偏转角λ2。

（4）地层坐标系O4X4Y4Z4。以地层层面的法向矢量为Z4轴，建立地层坐标系O4X4Y4Z4。Z4轴与重力线的夹角为地层倾角α3，Z4轴投影到水平面上与X1轴的夹角为φ3。

根据几何关系可以得到钻头轴线与地层法向的夹角ζ为

其中

（5）切削齿坐标系O5X5Y5Z5。以切削齿中心为O5，切削齿法向线为O5Z5轴，建立切削齿坐标系O5X5Y5Z5。

设给定钻头共有N个切削齿，其切削齿号码记为i∈（1，N）。令第i个切削齿的中心O5上的正压力为Fn，切削力为Fc。Fn与Z3轴夹角为切削齿的法向角γi。

初始时刻切削齿在钻头上的周向角为ωi，当钻头旋转了角度ωt，切削齿中心O5的径向线与钻头基准线的夹角ωc=ωi+ωt。随着钻头旋转，Fn围绕钻头轴线旋转，所形成的圆锥面与椭球面的交线为一椭圆。Fn与椭球面的交点与O3的距离是该切削齿力方向上可钻性级值Kd。

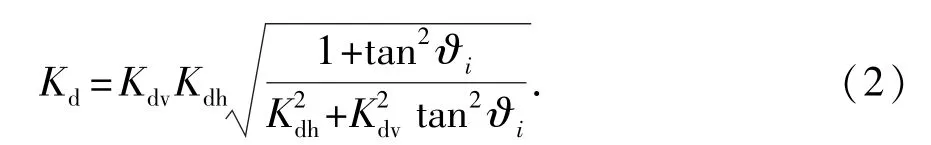
其中ϑi为Z5轴与Z4轴的夹角：

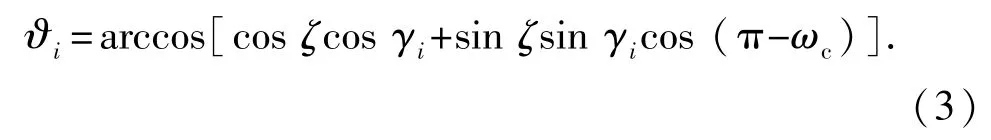
式中，Kdv为垂直于层面方向岩石可钻性；Kdh为平行于岩石层面方向岩石可钻性。

3　保径受力的计算方法

在定向钻井时，钻具组合给予钻头钻压W和侧向作用力Fl，使钻头冠部的切削齿切削岩石，钻头冠部受到岩石给予钻头的反作用力，其在轴向上的力为Fa，在侧向上的力为Fla。在侧向力作用下保径与井壁接触，保径受到井壁给予钻头的反作用力Flm。钻头达到力的平衡时：

为了分析保径长度对钻头受力的影响，使用剖面形状和布齿参数相同、保径长度不同的PDC钻头，在中国石油大学（华东）XY-2B型定向钻井平台上进行了定向钻进试验（图2、3）。用轴向加压装置给钻头提供钻压，用侧向加压装置给钻头提供侧向力。用压力传感器、扭矩传感器测定钻头的钻压、侧向力和扭矩，用位移传感器测定钻头的钻速。钻压为60 kN，侧向力为6 kN。

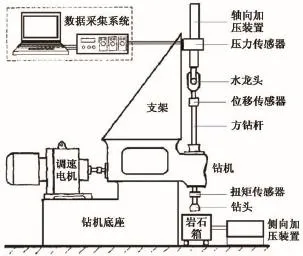
图2　XY-2B型定向钻井平台Fig.2 XY-2B drilling machine

如表1所示，当钻压和侧向力相同时，保径的长度越长，钻头冠部受力越小，保径受力越大。根据表1建立保径受力Flm与侧向作用力Fl的关系模型为

建立钻头冠部受力Fla与侧向作用力Fl的关系模型为

式中，Lb为保径长度。

表1　钻头保径的长度与保径受力的关系Table 1 Relationship between force and gage length

图3　5种不同组合形式的钻头示意图Fig.3 Five different combinations of bit

4　钻头冠部受力的计算方法

在定向钻井时切削参数随钻头旋转而不断变化［7］，切削齿受力也必然变化，因此有必要建立适用于定向钻井的PDC钻头受力模型。

设给定钻头上有N个切削齿，第i号切削齿的法向角为γi，侧转角为βi，其接触面的几何中心在钻头坐标系中的坐标为（Ri，Hi，θi）。钻头受力与切削齿受力的关系如图4所示。使用文献［7］的“定向钻井PDC钻头的切削参数计算程序”可以计算出第i号切削齿的切削面积Ai和接触弧长wi。

根据文献［8］中的单个切削齿受力计算公式，可以计算出该切削齿的受力（Fni，Fci），将其向钻头的轴向、切向和径向分解，就得到轴向分力Fvi、切向分力Fri和径向分力Frri。

式中，Fni为正压力；Fci为切削力；a1，b1，a2，b2为系数，与切削齿后倾角、线速度和岩石可钻性级值Kd有关。

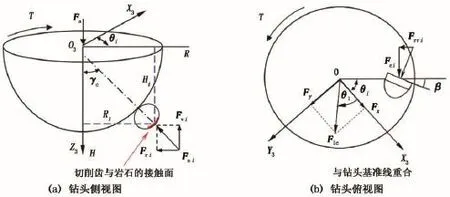
图4　钻头受力与切削齿受力的关系Fig.4 Relationship between force of bit and cutters

对各轴向分力求和，可得到钻头的轴向力Fa。各切向分力与切削半径Ri的乘积之和为钻头的扭矩T。将各径向分力向X轴和Y轴分解求和，可以得到两个方向的力Fx和Fy，其合力为钻头侧向力Flc，所以PDC钻头受力计算模型为

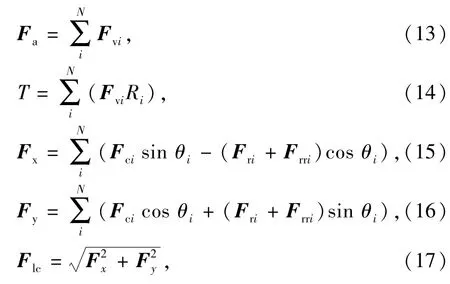
式中，Fa为钻头的轴向力；Fx和Fy分别为侧向力Flc在X轴和Y轴分力；Ri为切削半径；θl为方向角。

5　钻头的侧向力平衡计算方法

在垂直钻井时，由于布齿结构固有的各向异性，对所有切削齿求侧向的合力Flc不等于零，称该值为钻头的侧向不平衡力Flb。侧向不平衡力过大会导致PDC切削齿的冲击损坏。由于钻头的布齿结构决定了侧向不平衡力的大小和方向，所以对布齿结构的优化设计可以降低侧向不平衡力。实验和理论计算表明，对布齿结构的优化设计可以减小侧向不平衡力，但是不能够消除侧向不平衡力。

由于侧向不平衡力由钻头的各向异性产生，所以在定向钻进钻头受力平衡计算时也要将钻头侧向不平衡力考虑在内。根据纵横弯曲梁法，计算出钻具组合给予钻头的造斜力为Fα，变方位力为Fφ，其侧向合力为Fl。称Fl作用在钻头冠部的力为侧向作用力Fla。定向造斜时，Fa=W，Flc是侧向不平衡力Flb与侧向作用力Fla的合力，Flc=Fla+Flb。

若侧向不平衡力Flb大于侧向作用力Fla，则会导致井眼轨迹控制困难，井壁摩擦阻力增大等问题。须对布齿结构做优化设计，使侧向不平衡力Flb小于侧向作用力Fla。邹德永［13］针对垂直钻井提出了PDC钻头布齿结构优化设计方法，可以减小钻头的侧向不平衡力，该方法对定向钻井PDC钻头仍然适用。

在定向造斜时，侧向作用力Fla的方向一直保持不变，但钻头的侧向不平衡力Flb的方向随着钻头旋转而改变，所以Flc是随着钻头旋转而改变的值。为了时刻保持上述力平衡状态，钻头每旋转1°计算一次瞬态的钻头轴向力和侧向力，进而迭代计算出瞬态的钻头中心位移。

6　现场应用实例

图5　BTM115A9型PDC钻头出井图片Fig.5 BTM115A9 PDC bit

在鄂尔多斯盆地的HH42P38井中，使用石大华通公司的BTM115A9型PDC钻头（图5），从井深1664 m定向钻进到1695 m到达造斜点，之后又复合钻进到井深2290 m。滑动钻进进尺339 m，平均机械钻速3.46 m/h。复合钻进进尺288 m，平均机械钻速7.78 m/h。钻具组合为：Φ215.9 mm钻头+ Φ165 mm×1.5°螺杆9 m+4A11×410接头+MWD短节+Φ127 mm无磁承压钻杆9.45 m+Φ127 mm加重钻杆260 m+Φ127 mm斜台阶钻杆。钻压取40～100 kN，钻盘转速为45 r/min。因为钻进过程中使用了随钻测量设备，可以实时测量到钻压、扭矩和钻速。BTM115A9型PDC钻头的外径为215.9 mm，五刀翼双排齿，剖面形状是直线双圆弧形。主动性保径的长度为12.7 mm，被动性保径的长度为38.1 mm。如图6所示，使用上述方法预测钻头的钻速，钻速的预测值与实际测量值之间的平均误差为9.23%，说明本文的方法具有实用性。

图6　钻速与井深关系Fig.6 Relationship between drilling speed and depth

在胜利油田的临111-斜3井中，使用石大华通公司的BTM115Hy型PDC钻头（图7）从井深2 950 m定向钻进到3470 m，滑动钻进钻速2.24 m/h，工具面方位角为-20°～20°。钻具组合为：Φ215.9 mm的钻头+Φ171.5 mm弯角1.5°的单弯动力钻具+ Φ165 mm的无磁钻铤（9 m）+MWD+Φ127 mm的加重钻杆（150 m）+Φ127mm的钻杆。钻压为50～60 kN，钻头转速为螺杆马达转速。井斜角及方位角预测值与实测值的对比如图8所示。由图8可知，井眼轨迹的预测值与实际测井数据相吻合，说明本文中的方法能够较为准确地预测井眼轨迹。

图7　BTM115Hy型钻头出井图片Fig.7 BTM115Hy PDC bit

在胜利油田的夏503-斜5中，使用BTM115Hg型PDC钻头（图9）从井深2814 m定向钻进到3380 m，滑动钻进钻速1.97 m/h，工具面方位角为-40°～40°。使用的钻具组合和钻进参数同临111-斜3井。

图8　井斜角及方位角的预测值与实测值对比Fig.8 Experimental data and calculated value of well inclination and azimuth

对BTM115Hg型钻头的布齿优化设计，得到BTM115Hy型钻头。令钻压60 kN，侧向作用力6 kN，方向60°，分别计算两种钻头的中心点的侧向位移（图10）。钻头布齿优化设计前，BTM115Hg型钻头的侧向不平衡力为1582 N，其钻头中心一直在侧向作用力的左侧运动，钻头漂移角较大。优化设计后，BTM115Hy型钻头的侧向不平衡力为412 N，其钻头中心在侧向作用力的左右两侧运动，钻头漂移角较小，使工具面方位角变化范围变小。这说明钻头布齿参数的优化设计可以减小钻头的侧向不平衡力，减小钻头漂移角和工具面方位角变化范围。

图9　BTM115Hg型钻头出井图片Fig.9 BTM115Hg PDC bit

图10　优化设计前后钻头中心点的侧向位移对比Fig.10 Lateral displacement of bit center before and after optimal design

7　结 论

（1）PDC钻头的三维钻速不仅与钻具组合的力学性能有关，而且与PDC钻头的结构参数及地层可钻性各向异性有直接关系。

（2）根据具体的钻头结构参数和地层可钻性各向异性，通过数值计算可以获得钻头的轴向和侧向钻速，不须取得地层法向钻进效率。

（3）在钻头瞬态力平衡计算中，钻头侧向不平衡力过大将增大井眼轨迹控制的难度，通过对PDC钻头布齿参数的优化设计，可以减小钻头的侧向不平衡力，减小钻头漂移角和工具面方位角变化范围，增强井眼轨迹控制能力。

［1］ 高德利，刘希圣，黄荣樽.钻头与地层相互作用的三维宏观分析［J］.石油大学学报：自然科学版，1989，13（1）：23-31. GAO Deli，LIU Xisheng，HUANG Rongzun.Three-dimensional macroscopic analysis of interaction with the formation drill［J］.Journal of the University of Petroleum，China（Edition of Natural Science），1989，13（1）：23-31.

［2］ 齐林，周大千，江胜宗，等.用钻头与地层相互作用模式预测井眼轨道［J］.大庆石油学院学报，1995，19（4）：113-116. QI Lin，ZHOU Daqian，JIANG Shengzong，et al.Prediction of borehole trajectory by interaction model between drilling bit and stratum［J］.Journal of Daqing Petroleum Institute，1995，19（4）：113-116.

［3］ 于永南，吕英民.钻头与地层相互作用三种模型的一致性［J］.石油大学学报：自然科学版，1992，16（3）：60-65. YU Yongnan，LÜ Yingmin.Identity of three rock-bit in teraction models［J］.Journal of the University of Petroleum，China（Edition of Natural Science），1992，16（3）：60-65.

［4］ 李子丰，李敬媛.三维钻速方程及其反演模型［J］.西部探矿工程，1994，6（2）：8-11. LI Zifeng，LI Jingyuan.Three-dimensional drilling velocity equation and its reverse evolution model［J］.West-China Exploration Engineering，1994，6（2）：8-11.

［5］ STUDENT R，SIMON C.Learning curve benefits resulting from the use of a unique BHA directional behaviour drilling performances post-analysis［R］.SPE 110432，2007.

［6］ MENAND S，SELLAMI H.PDC Bit classification according to steer ability［R］.SPE 87837，2004.

［7］ 邹德永，王家骏，于金平，等.定向钻井PDC钻头的切削参数计算方法［J］.石油钻采工艺，2014，36（5）：5-9. ZOU Deyong，WANG Jiajun，YU Jinping，et al.Method for computing cutting parameters of directional drill bits［J］.Oil Drilling&Production Technology，2014，36（5）：5-9.

［8］ 王家骏，邹德永，杨光，等.PDC切削齿与岩石相互作用模型研究［J］.中国石油大学学报：自然科学版，2014，38（4）：104-109. WANG Jiajun，ZOU Deyong，YANG Guang，et al.Study on the interaction model of PDC cutter breaking rock［J］. Journal of China University of Petroleum（Edition of Natural Science），2014，38（4）：104-109.

［9］ 邹德永，张将海，王瑞和.PDC钻头力学模型的试验研究［J］.石油钻探技术，2005，33（2）：41-43. ZOU Deyong，ZHANG Jianghai，WANG Ruihe.The experiment study on mechanical model of PDC bits［J］.Petroleum Drilling Techniques，2005，33（2）：41-43.

［10］ 白家祉，苏义脑.井斜控制理论与实践［M］.北京：石油工业出版社，1990.

［11］ 尹宏锦.地层各向异性-岩石可钻性研究［J］.石油钻采工艺，1989（1）：15-22. YIN Hongjin.Research on formation anisotropy and rock drill ability［J］.Oil Drilling&Production Technology，1989（1）：15-22.

［12］ 邹德永，程远方，查永进，等.利用岩屑波速随钻检测地层可钻性及优选钻头类型［J］.石油大学学报：自然科学版，2005，29（1）：37-40. ZOU Deyong，CHENG Yuanfang，ZHA Yongjin，et al. Rock-drill ability evaluation and bit selection through ultrasonic velocity measurement on cuttings［J］.Journal of the University of Petroleum，China（Edition of Natural Science），2005，29（1）：37-40.

［13］ 邹德永.PDC钻头的数学模型与计算机化设计技术研究［D］.东营：石油大学石油工程学院，2004. ZOU Deyong.Study on the mathematical model and the computerizing technique about PDC bit design［D］. Dongying：School of Petroleum Engineering in University of Petroleum，China，2004.

（编辑 李志芬）

A novel prediction method of PDC bit's ROP in directional drilling

ZOU Deyong1，WANG Jiajun2，LU Ming3，CHEN Xiuping1，YU Jinping1
（1.School of Petroleum Engineering in China University of Petroleum，Qingdao 266580，China；2.College of Petroleum Engineering in Liaoling Shihua University，Fushun 113001，China；3.Drilling Research Institute of Petroleum Engineering，Western Drilling Engineering Company Limited，Karamay 834000，China）

In this study，a novel prediction method of PDC bit's ROP during directional drilling was established，in which the cutting action of the PDC bit，the mechanical action of BHA and the drillability anisotropy of rock formations were considered based on the instantaneous force balance principle.In the calculation of the total transient force on the PDC bit，the influence of the lateral unbalanced force on bit crown and the lateral force on bit gauge were accounted.The new method was verified using the experimental results of core drilling，in which the predicted well trajectory has a good agreement with the measured one.In using this method，the axial and lateral drilling rate of the PDC bit can be obtained by numerical calculation based on the parameter of the bit design and the drillability anisotropy of the rock formation，and no need to measure the normal formation drilling efficiency of the bit.In consideration of the transient force balance on the bit，the higher the lateral unbalanced force，the harder for well path control.The lateral unbalanced force on the PDC bit can be decreased by optimizing the PDC bit design，and the drift angle of the bit and the variation of the tool face azimuth can be also decreased.

drilling；PDC bits；drillability anisotropy；well trajectory；ROP；directional drilling

TE 21

A

1673-5005（2015）05-0082-07

10.3969/j.issn.1673-5005.2015.05.011

2014-12-10

国家“十二五”科技重大专项（05Z12020300）；中央高校基本科研业务费专项（12CX06025A）

邹德永（1962-），男，教授，博士，博士生导师，研究方向为油气井工程。E-mail：zouyan@upc.edu.cn。

引用格式：邹德永，王家骏，卢明，等.定向钻井PDC钻头三维钻速预测方法［J］.中国石油大学学报：自然科学版，2015，39（5）：82-88.

ZOU Deyong，WANG Jiajun，LU Ming，et al.A novel prediction method of PDC bit's ROP in directional drilling［J］.Journal of China University of Petroleum（Edition of Natural Science），2015，39（5）：82-88.