新型轴系联接结构的分析研究

赵 博，曾林锡，冀相安，陈文聘，马永明

（1.海军驻704所军事代表室，上海 200031；2.上海船舶设备研究所，上海 200031）

新型轴系联接结构的分析研究

赵 博1，曾林锡2，冀相安2，陈文聘2，马永明2

（1.海军驻704所军事代表室，上海 200031；2.上海船舶设备研究所，上海 200031）

对一种新型轴系联接结构——膨胀螺栓的结构设计进行了分析研究。在膨胀螺栓受力分析的基础上，从曲梁理论出发，建立了膨胀联结螺栓关键部件的应力应变关系，给出了膨胀螺栓结构的理论分析模型。将理论分析结果与有限元计算结果进行对比，验证了理论分析模型的有效性。本文提出的理论分析模型对膨胀螺栓的结构设计和应用具有实际的指导意义。

膨胀螺栓；曲梁理论；有限元方法

0 引言

轴系用膨胀螺栓结构是一种带有径向可扩张弹性衬套的紧配螺栓结构，它主要由六部分组成（图1），包括一个两端带螺纹的锥形螺栓、开口弹性衬套、超硬垫片、拧紧螺母及拧紧螺栓等。它利用弹性衬套与螺栓孔之间的径向过盈配合，实现了螺栓孔与膨胀螺栓之间的联结，从而将扭矩负载在轴系间传递下去。从结构上可见，膨胀螺栓联结对扭矩的传递是通过两个途径来实现的：一是依靠锥形螺栓在螺栓孔中的过盈配合所产生的抗剪力；二是依靠锥形螺栓预紧力所产生的联结法兰面间的摩擦力。这样可以使得联结更可靠，保证轴系设备的正常运行。膨胀螺栓结构通过拧紧小端拧紧螺栓，实现锥形螺杆、弹性衬套与法兰孔的过盈配合，只需手动扭矩扳手或气动扳手即可进行安装或拆卸，不需要任何高压工具及其它现场加工设备，可节省约 50%左右的工具和现场设备费用。由于不需要大型扭力扳手等大型工具，膨胀螺栓联接不需要较大的安装空间。其开口弹性衬套经多次使用后仍可恢复原尺寸，具有很好的再用性。因此膨胀螺栓联接非常适合应用在船舶轴系设备等安装空间狭窄、联接强度要求很高的场合。

目前国内对该种膨胀螺栓结构的研究比较欠缺，使用时主要依靠直接引进国外成品。在实际安装时，主要根据产品手册选取相应的预紧力和安全系数，缺乏对膨胀螺栓结构在使用过程中各部分受力变形情况的分析与掌握。本文综合利用弹性理论及有限元方法，建立了膨胀螺栓结构的理论分析模型，并用有限元进行验证，分析结果对膨胀螺栓的设计和应用具有重要的实用意义。

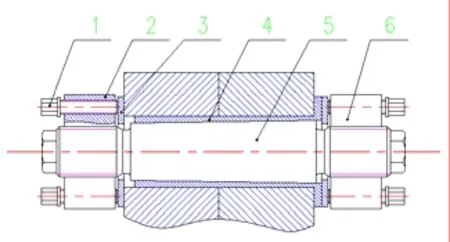
图1 膨胀螺栓结构示意图

1 膨胀螺栓结构的理论分析

图2为膨胀螺栓结构受力简图。为计算方便，引入以下基本假设：

1）弹性衬套和锥形螺栓接触面的全长上，接触压力为常量，即接触压力只是角度的函数而与轴向位置无关；

2）膨胀螺栓结构各部分的材料模型采用线弹性本构模型，满足弹性力学的基本假设。

图2 膨胀螺栓结构的力学分析模型

1.1 弹性衬套的理论模型和受力分析

由于膨胀螺栓结构中的弹性衬套部件与传统的衬套部件有较大差别，属于开口结构，其联接强度要小于传统的衬套部件，而同时弹性衬套的受力变形情况对膨胀螺栓的工作性能具有较大影响，因此本文首先对弹性衬套部件进行分析。

根据弹性衬套结构的受力情况及弹性力学相关理论，文中在计算弹性衬套的径向应力及环向应力时，将其简化为图3所示的平面曲梁模型。

图3 弹性衬套平面曲梁模型

根据弹性力学相关理论可知，在对图 3所示的平面曲梁模型进行分析时，需要知道确切的接触压力分布或变形情况，但由于目前缺少结构真实的应力和变形分布规律的分析资料，因此，根据弹性衬套的结构特点，文中引入如下假设：

1）弹性衬套在消除与法兰孔之间的间隙δ的过程中，忽略弹性衬套的弹性应变；

2）弹性衬套与锥形螺栓及法兰实现过盈配合的过程中，假设接触压力为均匀分布的常量。

根据本节的假设 1可知，弹性衬套在消除间隙过程中总的径向位移ur为：

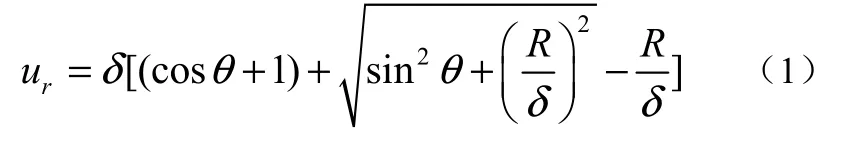
上式中的δ为间隙值，R为弹性衬套外表面半径。根据曲梁理论[1]，将式1代入如下方程，可以得到相应弯矩M、环向及径向正应力等值：

弹性衬套在实现过盈的过程中，其内外径表面分别与锥形螺栓及法兰孔实现完全接触，其内外径表面的径向正应力σr2等于接触压力，根据本节的假设 2及静力平衡方程，可以得到如下关系：

式中，r、R、Pi及Po分别表示弹性衬套的内外表面半径及相应的接触压力（图3）。利用拉美公式结合式 5给出的关系，可以得到弹性衬套内表面在过盈接触过程中的径向位移为[2]：

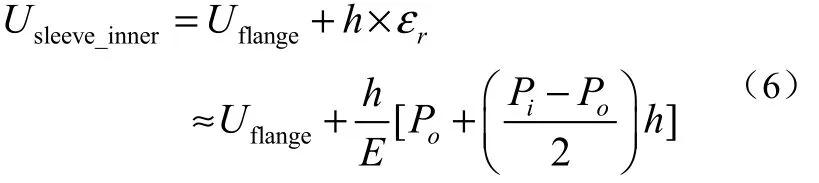
式中的 Uflange为法兰孔的径向位移，根据拉美公式，其表达式为：

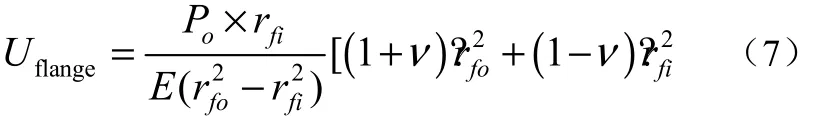
上式中，rfo和rfi分别为法兰分析模型的孔半径及外半径。通过将式7得到的径向位移值Uflange替代式1中的δ，然后将得到的ur代入式2～4，可以得到相应的环形正应力值 σφ2。

同时由于锥度的存在，弹性衬套在预紧过程中还存在一个轴向正应力σsz：

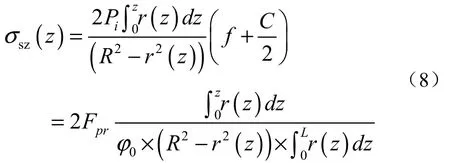
上式中：f为摩擦系数；C为锥度；r(z)为弹性衬套的内半径；L为衬套锥形螺栓的接触长度；Fpr为预紧力；φ0为开口弹性衬套的弧度，它与图 3所示的开口尺寸之间的关系为：

1.2 锥形螺栓的应力计算

锥形螺栓主要承受预紧力Fpr、与衬套的接触压力Pi及受扭矩 T作用时的剪切力作用。这三种作用力产生的应力分别为：

上式中，Fpr为螺栓受到的预紧力；Pi为接触压力；φ0为开口弹性衬套的弧度；rj为螺栓孔节圆半径；ra为螺栓孔的孔径。其中最大轴向正应力(σbz)max发生在图 2所示的直径为 D0的位置。而在承受扭矩的过程中，还需要对锥形螺栓受扭矩剪切作用处的强度进行校核。

1.3 小端拧紧螺栓的应力计算

膨胀螺栓的预紧力主要是通过小端拧紧螺栓提供的。拧紧螺栓在预紧过程中，所产生的轴向应力σnz为：

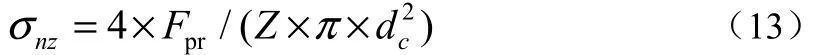
上式中，dc拧紧螺栓的直径；Z为拧紧螺栓的个数。同时，在螺栓预紧时，螺杆上的扭应力和正应力比值[3]：

上式中，ψ和 ρ分别为螺纹升角及当量摩擦角；

2 仿真验证

由于目前还不具备对膨胀螺栓进行实物试验的条件，同时也没有相应的文献资料可以参考，因此为验证本文提出的模型，特别是弹性衬套简化分析模型的适用性，文中将通过建立膨胀螺栓结构有限元分析模型，从而对理论分析结果进行验证。

验证模型的参数为：法兰孔的半径为定值，rfi=45mm；小端拧紧螺栓的半径rpr=9mm，个数Z=8；锥形螺栓和衬套：锥度C=1:30，结合长度为L=240mm，rbcmin=35mm，rbcmax=39mm；锥形螺栓在图2所示的最小处直径 D0=55mm；衬套的开口尺寸：Δh=2.6mm，摩擦系数取f=0.15；法兰：rfinner=45mm，rfouter=90mm。

2.1 分析模型结果

将模型参数代入式1～14，以预紧力Fpr为变量，得到不同预紧力时各部件的应力和位移值（表1）。

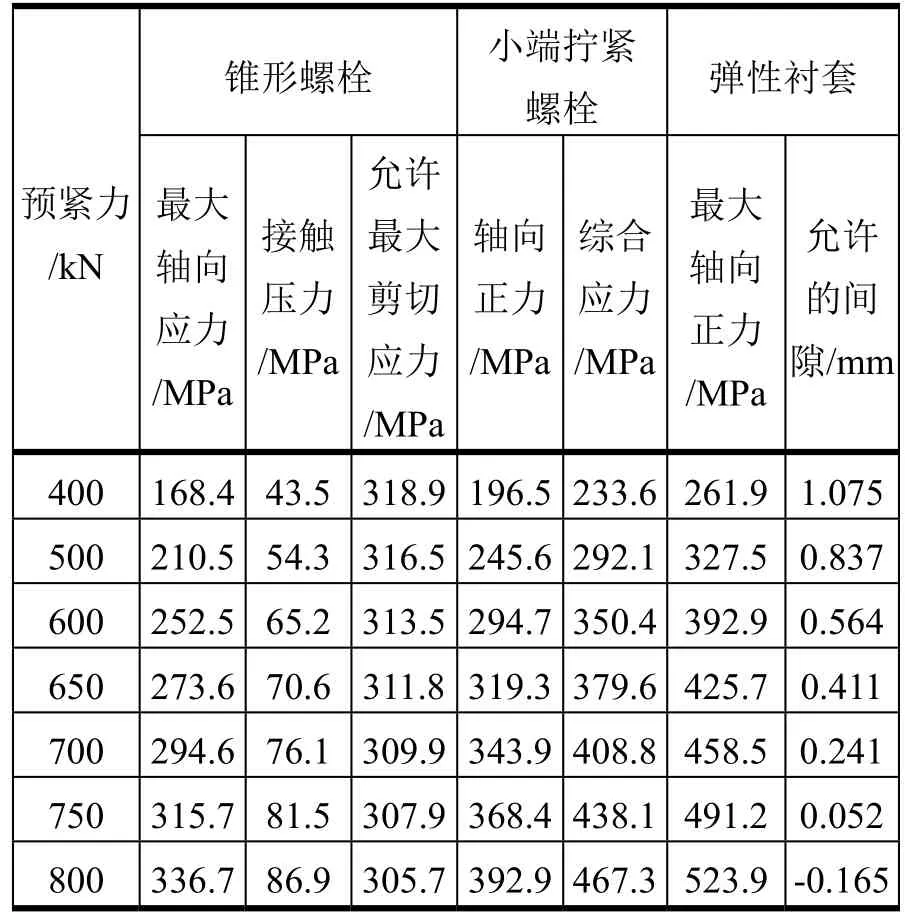
表1 理论模型计算结果

在上表的计算过程中，允许最大剪切应力和允许最大间隙值是根据部件的综合应力小于其材料的屈服强度而得到的。当预紧力为800kN时，弹性衬套的允许间隙为-0.165mm，这表明此时弹性衬套在预紧力的作用下已经失效。

2.2 弹性衬套有限元计算

本节将通过建立弹性衬套的二维平面应力模型来验证弹性衬套理论模型的适用性；根据上一节的分析，取间隙值δ=0.2mm，即弹性衬套外径rco=44.8mm。建立的模型如图4所示。

图4 膨胀螺栓结构的平面应力有限元模型

根据结果可知，除了在弹性衬套开口处等边界约束条件突变处之外的范围内，理论模型得到的结果与有限元模型的结果基本一致，其中：1）在消除间隙过程中，两种模型得到的弹性衬套外表面的位移值的误差小于5%（图5）；2）在过盈过程中，两种模型得到的径向位移值的误差小于5%（图6）；3）环向正应力值的误差小于10%（图7）。

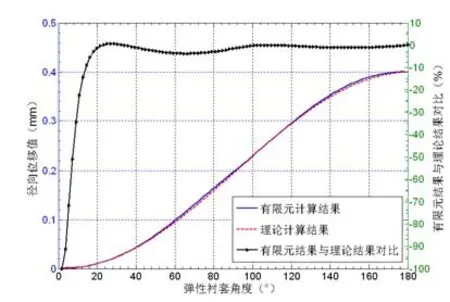
图5 有限元模型和理论模型得到的弹性衬套位移结果对比

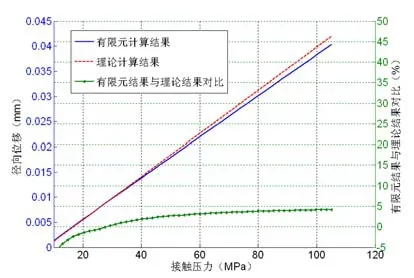
图6 有限元模型和理论模型得到的弹性衬套径向位移结果对比

图7 有限元模型和理论模型得到的弹性衬套环向正应力结果对比

2.3 膨胀螺栓结构有限元计算

文中建立了膨胀螺栓结构的三维有限元分析模型（图 8），用于分析锥度及扭矩对膨胀螺栓结构联结性能的影响。由于法兰面在结构、载荷和约束上都有周期对称性质，因此本文中建立的有限元模型只是整体模型的1/12。

根据计算结果可知：1）锥度对锥形螺栓及弹性衬套轴向正应力的分布具有较为明显的影响，由于锥度的存在，导致弹性衬套的最大应力出现在大锥端处（图9），而不是承受扭矩作用的弹性衬套中间部位；2）膨胀螺栓结构中，最大应力出现在弹性衬套上，因此在实际设计及使用中，应重点对弹性衬套的强度性能进行分析；3）理论模型得到的弹性衬套及锥形螺栓的轴向应力分布与有限元计算结果较为接近，除端部由于边缘效应误差较大外，其余部位的误差小于5%（图9、图 10）。

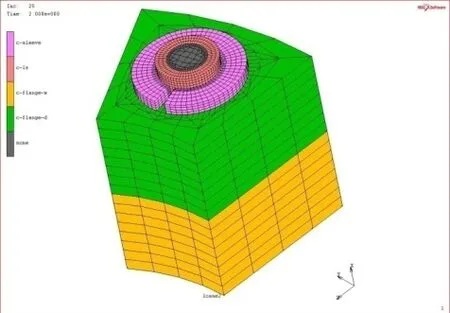
图8 1/12的膨胀螺栓三维有限元模型

图9 弹性衬套在受预紧力作用时的轴向应力

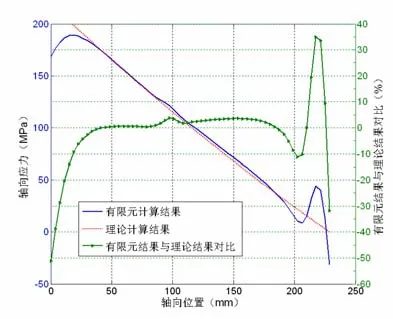
图10 锥形螺栓在受预紧力作用时的轴向应力

3 结论

1）通过理论计算和有限元分析的对比研究，验证了利用曲梁模型对弹性衬套结构进行分析的有效性。除衬套的端部边界外，位移分量和应力分量的相对误差值在10%之内。

2）弹性衬套的环向正应力与间隙值δ及弹性衬套厚度h近似成正比；弹性衬套的轴向正应力与弹性衬套厚度h的平方近似成反比。

3）锥度对锥形螺栓及弹性衬套轴向正应力的分布具有较为明显影响；其中，由于锥度及弹性衬套的结构特点，其轴向正应力与摩擦系数近似成正比。

4）简化分析模型是在曲梁理论假设基础上得到的，分析过程中用综合分布压力代替了内外径表面的接触压力分布情况，该假设导致理论模型得到的径向正应力与有限元得到的结果相差一个10MPa左右的常值。

5）本文提出的弹性衬套理论计算模型及相应的计算方法，可为膨胀螺栓的结构和参数优化设计、计算等提供一定的参考价值。

[1] 刘鸿文, 林建兴, 曹曼玲. 高等材料力学[M]. 北京: 高等教育出版社, 1985.

[2] 许定奇, 孙荣文. 过盈联接的设计、计算与拆装[M]. 北京: 中国计量出版社, 1992.

[3] 卜炎. 螺纹联接设计与计算[M]. 北京: 高等教育出版社, 1995.

[4] 陈火红. Marc有限元实例分析教程[M]. 北京: 机械工业出版社, 2002.

Study on New Bolt-joint Structure for the Shafting System

ZHAO Bo1, ZENG Lin-xi2, JI Xiang-an2, CHEN Wen-pin2, MA Yong-ming2
(1. Navy Representative Office at No.704 Research Institute, Shanghai 200031, China；2. Shanghai Marine Equipment Research Institute, CSIC, Shanghai 200031, China)

This paper introduces the structure characteristics and main designing points of a new bolt-joint structure, expansion bolts. On the basis of force analysis of expansion bolts, starting from the curve beam theory in elasticity, the analysis model of expansion bolt is developed. The validity of results calculated by analysis model has been checked by the results obtained by the finite element method. The analysis model developed by this paper will be helpful in the design and application of the expansion bolts.

expansion bolts; theory of curved beam; finite element method

U664.22

A

10.16443/j.cnki.31-1420.2015.06.002

赵博（1977-），男，硕士。研究方向：舰船机电设计研究。