Px平差法在精密工程测量中的应用初探

黄吉来++王丹

摘 要：精密工程测量的主要任务在于对空间中具体实体的精密测量描绘和抽象几何实体的精密测设实现的理论、方法和技术的研究。为了更大程度地提高测量的精度，以获得更为可靠的测量成果，根据工程的要求和现场的具体条件进行特种精密工程测量，可采用通过精度分析，拟定切实可行的观测方案以及使用适合于观测方法和观测值种类的平差方法。本文采用带权约束参数平差法（P x平差法），对不锈钢冷轧生产线的滚筒位置检验校正中的数据处理问题进行分析和研究，取得较好效果。

关键词：平差法 精密工程 测量 应用

中图分类号：P207.2 文献标识码：A 文章编号：1672-3791（2015）07（b）-0000-00

作为一条精密的自动化生产流水线的不锈钢冷轧生产线，其设备极其精密，总长约20m，据此可以严格控制产品的质量。通过感应滚筒测量其厚度，不锈钢原坯钢板进入轧机室冷轧，然后经过长度为1.6m、直径400mm的感应滚筒，检验已轧钢板的厚度。因此，滚筒轴线要严格垂直于轧机纵轴线，偏差应≤±0.08mm；滚筒轴应水平，两端高差应≤±0.08mm。两个感应滚筒轴线的垂直度和水平度都要要求检验，若偏差大于上述要求，则校正滚筒轴，直到偏差满足上述要求。

1 精密工程测量的定义和特点及平差理论的测量

研究地球空间中具体几何实体的精密测量描绘和抽象几何实体的精密测设实现的理论、方法和技术，就是精密工程测量的主要任务。它代表着工程测量学的发展方向。顾名思义，所谓的精密就是精确严密。要求高精度测量是精密工程测量的最大特点。测量平差时广泛应用的就是最小二乘法。平差、滤波和推估都是最小二乘法的配置；概括平差模型就是附有限制条件的条件平差模型。它是由现代平差模型和各种经典的组成的统一模型。在对模型误差的研究上，测量误差理论主要包括：平差中函数模型误差、随机模型误差的鉴别或诊断、模型误差对参数的影响以及对参数和残差统计的影响。由于需要检验变形监测网参考点的稳定性，这便导致了出现和发展自由网平差和拟稳平差，并且研究观测值粗差促进了控制网可靠性理论，以及可区分性理论的研究和发展了变形监测网变形和观测值粗差。稳健估计（或称抗差估计）是出现在针对观测值存在粗差的客观实际条件下。因为针对病态的可能存在于发放成系数阵中，有偏估计得到了发展。稳健估计和有偏估计与最小二乘估计相区别，成为非最小二乘估计。

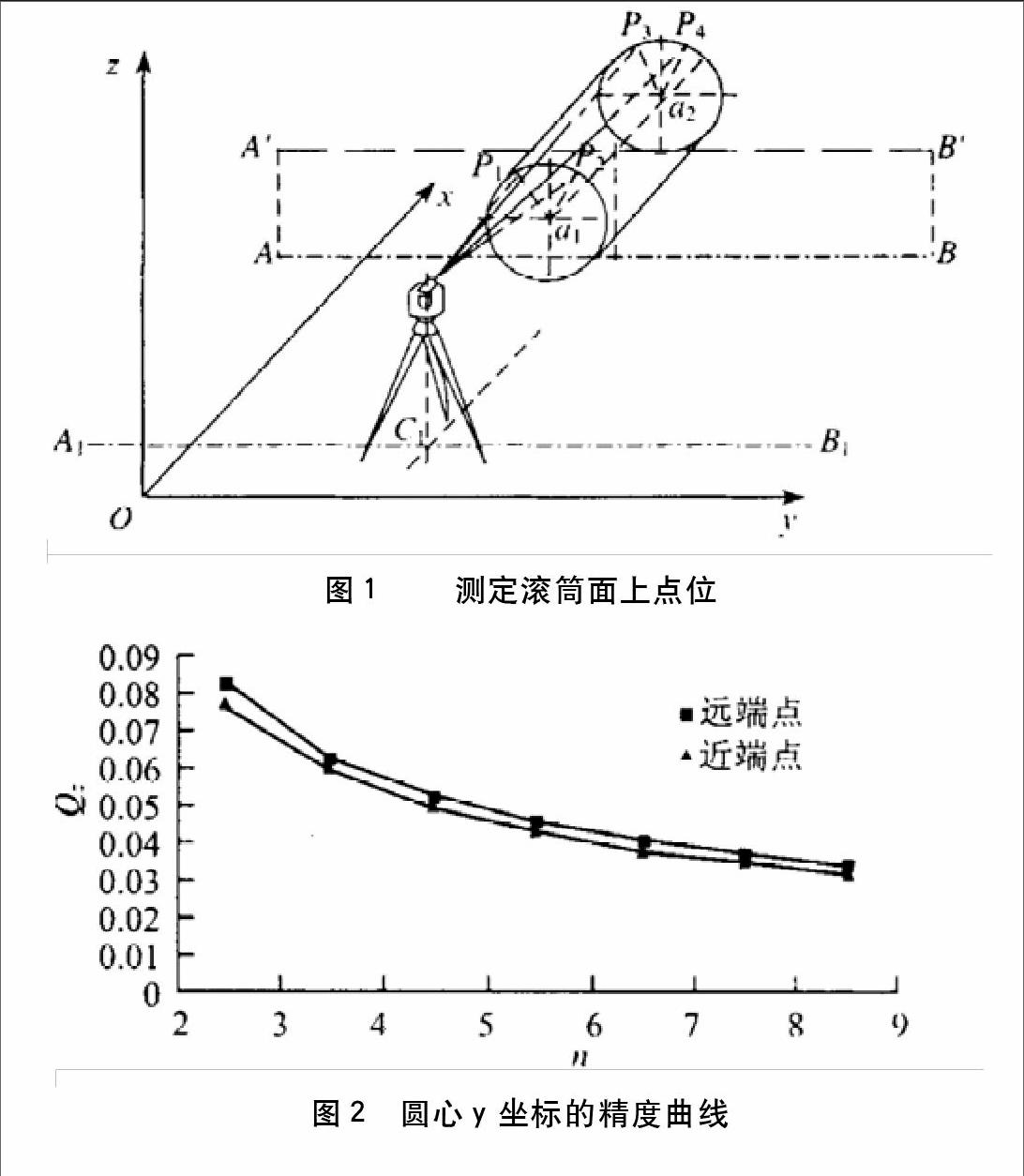
2 利用极坐标法对空间点三维坐标的精度估算进行测定

如图所示，建立平行于纵轴线AB的轴线A?B?，将全站仪安置在平行轴线上与滚筒轴的一端C1，滚筒面两段圆周上的若干点（如图中的P?，P?，P?，P4等）的三维坐标可使用极坐标法来分别测定。滚筒面圆周约有120°的暴露部分，并且由平行于滚筒轴的x轴、平行于生产线纵轴的y轴以及作为铅垂线的z轴组成一个独立坐标系。可以以滚筒面圆周上各店三维坐标及滚筒的半径为依据计算出滚筒两端圆心（如图中的a?，a?）的三维坐标，并且根据此可将滚筒轴线的垂直和水平偏差计算出来。设x0，y0，z0为仪器两轴的中心坐标，以方位角α、天顶距β、斜距s作为对目标P的观测值，则可根据中心坐标和目标P的观测值以及公式x=x0+△x=s*cosαcosβ+x0、y=y0+△y=s*sinαcosβ+y0①和z=z0+△z=s*sinβ+z0计算出待定点P的空间坐标，而后根据协方差传播定律可得到P点坐标的方差（mx 2=（△x*m s/s）2+（ △y*mα/ρ）2+ （△x*△z*mβ/Dρ）2 、my 2=（△y*m s/s）2+（△x*mα/ρ）2+（△y*△z*mβ/Dρ）2 ②、mz 2=（△z*ms/s）2+（D*mβ/ρ）2）和协方差（mxy=△x*△y*ms2/s2-△x*△y*m2 s/ρ2+△x*△y*△z2*mβ2/D2* ρ2 、mxz =△x*△z*ms2 /s2-△x*△z*mβ2/ρ2 ③ 、myz =△y*△z*ms2/s2-△y*△z*mβ2/ρ2）。从图中还可看出点位的水平横向误差my和铅垂方向mz 是滚筒轴的垂直度与水平度的关键，所以根据公式②和③，在一定的测角和测距精度条件下，应该限制△y与△z的数值（≤150mm）。因此，可根据各种能达到的测角和测距精度以及现场条件，然后用极坐标法估算测定点位的误差，经过比较分析从而决定采用有效的方案。

3 平差法计算圆心坐标

要想计算出滚筒两端圆心的坐标，可根据滚筒圆周上的两点坐标和滚筒的半径。比如也可以用平差方法求得圆心的坐标来测量圆周上的多于两点。将用极坐标法测定的点位坐标作为“观测值”可以采用带权约束参数平差法（P x平差法）。为求出其圆心的精确坐标和精度，可用机械量测工具精确测定的半径一起进行平差计算。

3.1带权约束平差法的基本原理

方程式Pm ：V m=A?X?+A?X?+I m 和P x ：V x=A x X?+Ix ④是带权约束参数平差的观测值方程式，也叫做误差方程式。在方程式中，将观测值的改正值设为V m ；将已知点坐标的改正值设为V x；将已知点和已知点平差后坐标改正值（未知参数）分别设为 X?和 X?；将未知数的参数设为A?和A?，而I m和Ix 为观测值方程式常数项；并且Pm为网中m个观测值的权。因为观测值之间是相互独立的，为了方便计算，Pm作为对角阵，取先验单位权中的误差σ=1，因此，观测值方差的倒数就是Pm矩阵的对角元素；由于σ=1，所以取P x为已知点的坐标值的权矩阵，那么可以用公式P x=Dx-1 ⑤进行计算.在该公式中，D x表示已知点的先验方差协方差矩阵，可以从点平差资料中查得它或者根据定精度通过估算而得。以公式④为基础，按照最小二乘原则可组成方程式NX+ATPL=0⑥，其中只有X为未知参数，所以通过公式可解出未知参数为X=-Q x ATPL（其中Q x=N-1 ⑦）那么由此可见，通过先求出已知点的先验方差协方差阵D x，求出D x的逆，得到其权阵，然后再讲已知点的坐标作为具有权阵P x的虚拟观测值，最后一般观测值与它一起组成方程式求解德到未知参数，这便是带权约束参数平差与经典平差的差别。因此，又把带权约束参数平差叫做P x平差。可先根据公式D x=σ02 Q x ⑧计算未知参数平差后的方差协方差阵来评定P x的精度。然后根据⑧计算出σ0=VTPV/r（σ0为平差后的单位带权中误差）⑨VTPV= VT m P m V m+ VT x P x V x ，r=（m+d）-n.其中设m为观测值的个数；具有先验方差协方差的已知点坐标数为d；而n则是未知数的个数，它包括坐标改正值未知数以及水平方向观测中的测站定向未知数；多余观测数设为r。在本精密工程中，将高精度观测值（可以用千分尺测量）用滚筒的半径值代替，有误差的已知点在圆周上用极坐标法测定的点代替，按照公式②和③计算其坐标的方差和协方差，最后再用P x平差法计算滚筒两端圆心点的坐标。

3.2确定观测点数

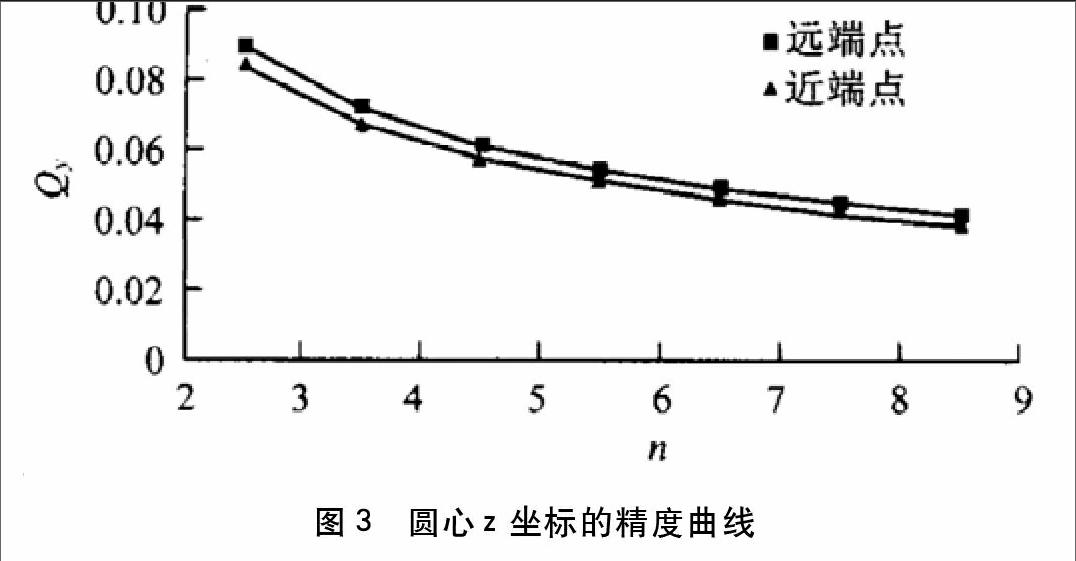
已经知道滚筒面圆周约有120°的暴露部分，观测点数在圆周上不宜过密。在圆周上，可能的观测点数为3-9点。在模拟计算圆心坐标的误差变化情况，使用Px平差程序能更好地选取恰当的观测点数，用图表将最后模拟 计算的结果表示出。由所给图可知，图2为圆心y坐标的协因数变化曲线，图3所示为圆心z坐标的协因数变化曲线。

图2 圆心y坐标的精度曲线

图3 圆心z坐标的精度曲线

4 结语

自由网拟稳平差分析变形监测数据是平差方法中很有效的一种方法。它讨论了网点稳定性检验结果是会手变形监测网的网型结构所影响的，同时也指出，其余动点的位移当在网中拟稳点组无法独立构成网形时在各观测周期间的坐标值是会产生影响的，其点位的稳定性分析结果也会受到扭曲。由此可得出，任何一种变形分析的平差方法都具有自己适用范围，要想取得满意的结果，那么就要在了解工程性质和掌握其先验信息的技术上，选择一种合适的平差分析法。其精度要求是用常规测量方法难以达到的特殊密工程测量是本文所讨论的主要内容。因此，本文提出可以很好地解决这一问题的测量方案和平差。在施测的方案中，对于特种精密工程的测量，根据测量仪器的特点，充分利用和发挥它的特长，扬长避短，为使测距的精度影响减少到零，可采用高精度的测角方式而不是采用精度较差的测距手段，与此同时，在进行数据处理时为提高计算成果的精度和可靠性应采用恰当的平差方法。现代化工厂的标志是工业自动化生产线，但是有着极高精度要求的生产线上的轴线检测有传统的机械量具手段是难以满足这一要求的。为了能够很好地解决这一问题，可采用现代化的精密工程测量技术，在当今各个学科之间，这也体现了相互借鉴相互渗透的发展趋势。

参考文献

[1] 顾孝烈.城市与工程控制网设计[M].上海：同济大学出版社，1991.

[2] 鲍峰.带权约束参数平差及其应用[J].同济大学学报，1995，23（2）：181-185.

[3] 张正禄，邓勇，罗长林，等.论精密工程测量及其应用.测绘通报，2006（5）：17-19.

[4] 张松林，张正禄，罗年学.GPS平面控制网的模拟设计计算方法及其应用[J].武汉大学学报（信息科学版），2004（8）.

[5] 张正禄，邓勇，罗长林，等.精密三角高程代替一等水准测量的研究[J].武汉大学学报（信息科学版），2006（1）.