基础沉降规范法与数值模拟比较研究
2015-10-15邵艳红周艳生
孙 超 邵艳红 周艳生
(吉林建筑大学测绘与勘查工程学院,长春 130118)
0 引言
基础沉降计算是地基基础工程设计的三大难题之一.计算地基沉降的最终目的,是在建筑设计中,预知该建筑物建成后所产生的最终沉降量,并判断是否超出允许范围,以便在建筑物设计时,采取相应的工程措施提高建筑物的安全性[1].在进行地基基础设计时,不仅要满足强度要求,同时也要满足变形要求.对此,国内的许多专家、学者对其进行了深入的研究,但最终没有得出统一定论.本文针对柱下独立基础进行了附加应力和沉降计算,通过规范法计算与FLAC3D数值模拟,对沉降结果、附加应力,进行比较分析,阐述了产生差异的原因,论证了FLAC3D有限差分法在计算基础附加应力和沉降方面的合理性.
1 规范法计算基础沉降
1.1 计算方法
根据《建筑地基基础设计规范》[2],考虑了附加应力系数的概念,得到了沉降计算的公式:
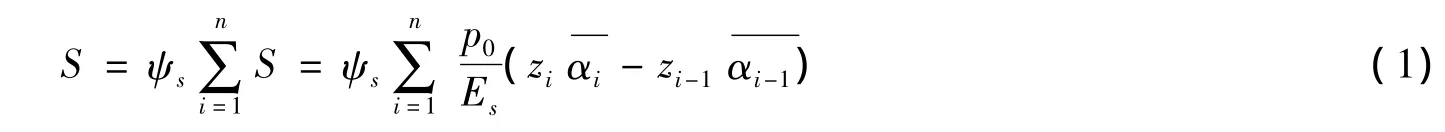
式中:S为柱下独立基础的最终沉降量(mm);ψs为沉降计算经验系数;p0为对应于荷载效应准永久组合时的基础底部的附加应力(kPa);Es为基础底下第i层土的压缩模量(MPa);zi,zi-1为基础底面至第i层土,第i-1层土底面的距离(m);αi,αi-1为基础底面计算点至第i层土、第i-1层土底面范围内的平均附加应力系数.
1.2 沉降计算及结果
柱下独立基础,受到集中荷载1 190kN,基础底面尺寸长4m,宽2m,基础埋深d=1.5m,土层、基础及柱的物理力学参数如表1:

表1 物理力学参数
经计算知,基础底面的附加应力为150kPa,根据计算深度的要求,计算到基底以下4.5m处即可,其沉降量为67.74mm,为了与数值模拟的结果进行对比,又计算至基底以下6m处,总沉降为73.22mm,其中取1.2,经修正后的总沉降为 87.86mm.
2 基础沉降的数值模拟
2.1 模拟模型及参数
本次模拟分别采用FLAC3D中的摩尔-库仑模型和弹性模型两种方式,在两种方式下建立共同的几何模型.该模型的水平方向取12m,分48个单元,宽度取12m,分为48个单元,高度取7.5m,分为30个单元格,基础长为4m,取16个单元,宽2m,取8个单元,高度为0.5m,取2个单元,柱取长宽均为0.5m的方柱,为2个单元,高度取1.5m,取6个单元,模型所需参数如表1,在柱和基础之间设定接触面,定义为interface 1,柱侧面、基础侧面和土体间设定接触面为interface2,接触面参数见表2.
(1)模型立体图见图1;基础和柱的剖面图见图2.

图1 模型立体图
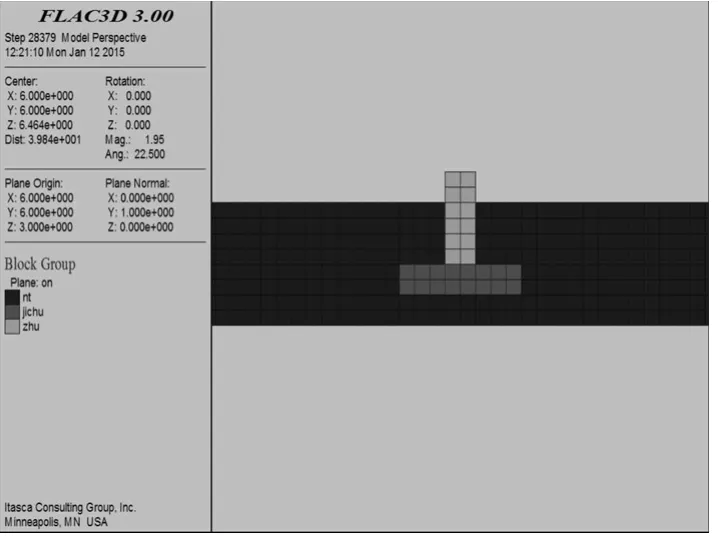
图2 基础和柱的剖面图
(2)接触面参数表见表2,

表2 接触面参数
2.2 采用摩尔-库仑模型和弹性模型的沉降模拟结果及分析
由图3可知,基底处的沉降最大为102.36mm,图4中基底处的最大沉降为36.37mm.沿着深度方向,沉降逐渐减小,这是由于在基底处附加应力最大,产生的沉降值最大,在深度方向上,附加应力逐渐减小,引起的位移增量减少,致使总的沉降减少.
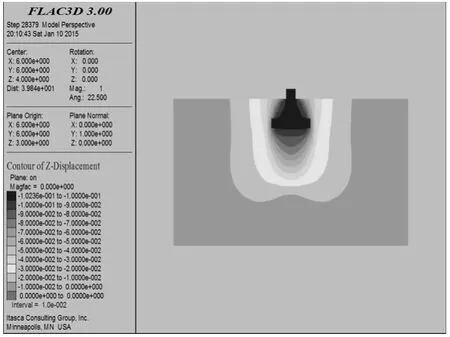
图3 摩尔-库仑模型沉降云图
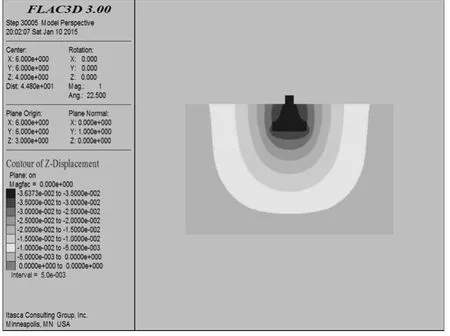
图4 弹性模型沉降云图
2.3 采用摩尔-库仑模型和弹性模型的总应力、自重应力模拟结果及分析
在摩尔-库仑模型下,由图5可知,基底处总的应力值为150kPa,自重应力为20.1kPa,经过计算得到附加应力值为129.9kPa,基底下3.5m处的的附加应力为75.12kPa,6m处附加应力为16.55kPa,因而,在基底处附加应力最大,随着深度的增加,数值逐渐减小.同理,在图6的弹性模型下也能得到此规律.

图5 摩尔-库仑模型总应力和自重应力云图

图6 弹性模型总应力和自重应力云图
3 对规范法、摩尔-库仑、弹性模型计算的位移、附加应力曲线分析
3.1 规范法、摩尔-库仑和弹性模型模拟的沉降曲线(如图7所示)
由图7可知:基底处弹性模型产生的沉降量最小,为36.06mm,采用规范法计算经修正后的沉降为87.86mm,摩尔-库仑模型产生的沉降量最大,为102.1mm,并且三者的沉降曲线随着深度增加均递减.
由于规范法假定地基土在水平方向是不能膨胀的,实际上仅当基底面积很大或压缩土层较薄时,才比较接近这种情况,计算结果偏小[3].而FLAC3D[4]采用的摩尔-库仑模型模拟,假定的土体是一种弹塑性土体,接近真实土性,得到的沉降结果与实际更为接近.
3.2 规范法、摩尔-库仑和弹性模型模拟的基底下附加应力曲线(如图8所示)
由图8可知:
(1)弹性模型在基底处的附加应力为56.2kPa,-6m深度处的附加应力为16kPa,摩尔-库伦模型基底处为109.9kPa,-6m处的附加应力为16.55kPa,规范法计算基底处为149.75kPa,-6m处为61.16kPa;
(2)FLAC3D中采用摩尔-库仑模型和弹性模型得到的附加应力均随深度呈曲线衰减,这是由于随深度增加,土中产生应力扩散现象,导致附加应力减小.
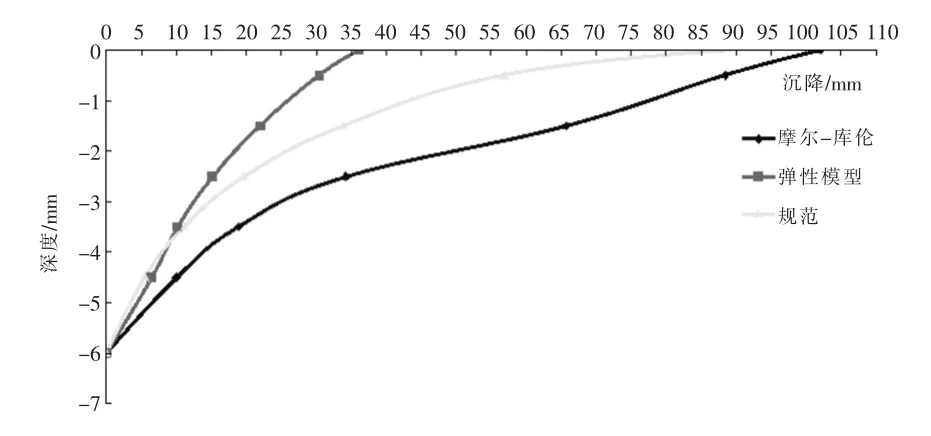
图7 基底以下土的沉降曲线
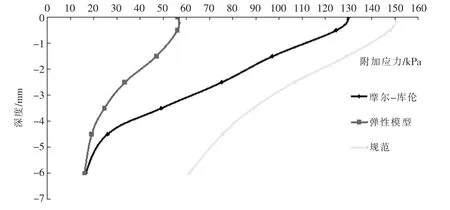
图8 基底以下土的附加应力曲线
4 结语
(1)采用规范法、数值模拟,得到基础下的附加应力在基底处最大,由于附加应力具有一定的扩散性,它不仅分布在基底范围内,而且在基底以外相当大的范围内也存在.在纵向上,随着深度的增加,呈现曲线递减的规律,在水平方向上,基底中轴线上最大,随距中轴线距离越远而越小,符合附加应力扩散理论;
(2)在基础沉降量的计算中,规范法虽然也采用了分层总和法的假定,但引入了修正系数,对计算结果进行了修正,使结果与实际值误差减小,但修正系数的取值跨度很大,从而导致计算值与实际值有较大的误差,计算的最终沉降量数值较小,偏于保守;
(3)与均质地基相比,当地基土呈上软下硬状态时,出现应力集中现象,得出的沉降量数值偏大;地基土呈上硬下软状态时,出现应力扩散现象,得到的沉降量数值偏小;
(4)数值模拟中,采用摩尔-库仑模型模拟基础沉降时,由于其是弹塑性模型,能较好的反应土体的真实情况,得到的沉降值较为合理,与实际工程较为接近.
[1]赵明华,俞 晓.土力学与基础工程[M].武汉:武汉理工大学出版社,2010.
[2]中华人民共和国住房和城乡建设部.建筑地基基础设计规范(GB50007-2011)[S].北京:中国建筑工业出版社,2011.
[3]邓洪亮.地基沉降量方法探讨[J].洛阳大学学报,1998,13(2):58-59.
[4]陈育民,徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京:中国水利水电出版社,2013.
