综合热扩散和全变分模型的自适应图像去噪模型
2015-10-14图妮萨古丽·达伍提等
图妮萨古丽·达伍提等

【摘 要】讨论了各向同性热扩散(TD)方程模型和各向异性全变分扩散(TV)方程模型对图像去噪的影响。在此基础上提出了一个改进的自适应混合模型,所提出的模型根据图像的信息能够自适应每个区域。该模型进行扩散图像的更加平坦区域,而较少的扩散在图像的边缘,得到了较好的去噪效果,同时保持边缘。比较了这三个模型对图像去噪的效果。数值实验结果表明,改进的自适应混合模型具有更好的去噪效果。
【关键词】图像去噪;热扩散(TD)模型;全变分(TV)模型;自适应混合模型
【Abstract】The paper mainly discussed the influence of the TD (isotropic) and TV (anisotropic) equation models on image denoising. And on the basis of this research ,the paper proposes an improved model, named adaptive hybrid model .The newly proposed model can be adapt to each area according to the information of image. The model diffusesthe smooth areas of the image, but diffuses less on the edge of the image, for which it reaches to better effect of denoising. And maintain the edge in the meantime. After comparing the three kinds of with each other, the numerical results of the experiment indicates that, the improved adaptive hybrid model has better effect of denoising.
【Key words】Image denoising; Thermal diffusion(TD) model; Total variation(TV) model; Adaptive hybrid model
0 引言
图像去噪的所有方法的目的是通过去除噪声恢复和提高图像特征,因为噪声具有高频率,所以很难去除图像中的噪声,图像去噪是去除图像中噪声的同时尽可能多的保留图像中原有重要的细节性息,解决该问题的最有效的方法是现在许多人在寻找的一个问题。图像去噪有很多方法,比如,统计模型去噪[1]、小波变换去噪[2-3]和偏微分方程去噪[4]。
偏微分方程的图像去噪理论最初是从Gauss滤波引入的[5]。理论研究和数值计算均表明,大部分局部滤波算子都能转化为微分算子。该方法能在有效地去噪的同时能够更好地保留图像的边缘等信息,在图像分割、图像增强、图像恢复中都取得了较好的效果,受到了越来越多的关注。它的发展过程经历了线性到非线性、各向同性(Isotropic)延伸到各向异性(An-isotropic)[6]。
各向同性扩散模型是通常用于平滑的图像。这模型的线性扩散方程使我们能够很好的去除噪声。全变分(TV)模型与热扩散(TD)模型分别良好的保持图像边缘和图像平滑。尽管如此TD模型将图像的模糊边缘中消除噪声,同时在平坦区域内处理TV模型所产生的效应。
本文在分析TD模型和TV模型的基础上,讨论了扩散模型对图像去噪的影响,然后定义了一个新的能量泛函,实验结果表明,改进的自适应混合模型能够有效的进行图像去噪。
1)在图像中包含多个图像特征的区域(如边缘等),新模型将保持图像的边缘起到很好的作用,即这种模型将突出全变分(TV)模型,因此?琢应接近于1。
2)在图像的平坦区域,它包含较少的图像特征和多噪声,该新模型将突出TD模型的作用,因此?琢应接近0。
综上所述,所提出的自适应混合去噪模型根据图像中每一像素点的梯度信息,自适应选取去噪模型中决定平滑强弱的参数?琢,从而达到较好的去噪效果。
线性热扩散(TD)模型是适定的,这意味着TD模型是稳定的[9],TV模型是更稳定的[10]。新的模型是这两种模型的结合,所以它是收敛了。
3 实验结果及分析
为了说明本文自适应图像去噪模型的有效性,我们进行了大量的仿真试验,现以Lena和Peppers图像为例进行说明和分析。
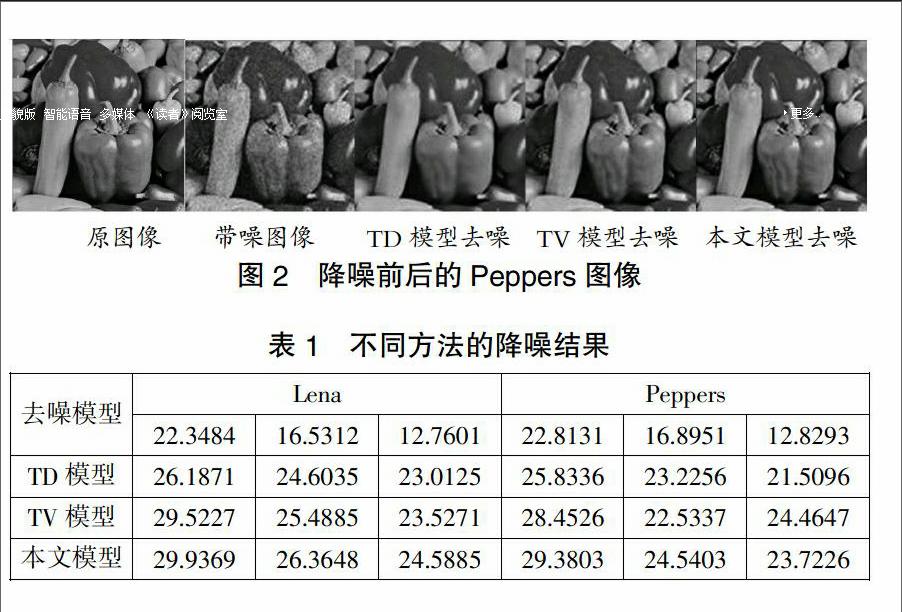
利用被噪声污染的Lena和Peppers图像作为输入,它们的大小均为512x512,灰度级为256,用峰值信噪比(PSNR)作为评价的客观标准,分别对热扩散TD去噪模型,全变分TV去噪模型和本文提出的综合TD模型和TV模型的自适应图像去噪模型进行了比较。在本试验的仿真中,取Gauss滤波器的窗口大小为3×3,方差为0.1。图1和图2分别为降噪处理前后Lena和Peppers图像的视觉效果。表1是不同噪声条件下,各模型对测试图像的滤波结果。
仿真数值实验表明本文所提出的综合TD模型和TV模型的自适应图像去噪模型降噪效果明显,人眼能直观感受图像质量的改善,其峰值信噪比(PSNR)在高噪声水平下,较其他两种去噪模型至少高1.0dB左右。
4 总结
本文通过研究PDE方程在图像去噪领域的基础模型:TD模型和TV模型,重点分析了各向同性热扩散方程模型和各向异性全变分扩散方程模型对图像去噪的影响,并且提出了综合TD模型与TV模型的自适应混合模型。数值实验结果表明,改进的自适应混合模型的峰值信噪比的值均比TD模型和TV模型的值大,这说明新的自适应混合模型具有更好的去噪效果。
【参考文献】
[1]G.Aubert and P.Kornprobst. Mathematical Problems in Image Processing PDEs and the Calculus of Variations[M]. 2nd edn. Springer, New York,2006.
[2]Donoho D L.Denoising by soft-thresholding [J].IEEE Transactions on Information Theory,1995,41(33):613-627.
[3]T.AbdukirimTurki, M.Hussain, K.Niijima,and S.Takano.The dyadic lifting schemes and the de-noising of digital image[J].International Journal of Wavelets, Multi- resolution and Information Processing, 2008,6(3):331-351.
[4]L.Rudin,S.Osher,and E.Fatemi.Nonlinear TotalVariation Based NoiseRemoval Algorithms[J]. Phisica D,1992,60(1-4):259-268.
[5]A.P.Witkin . Scale-space filtering. 8th International Joint Conference on Artificial Intelligence[C], Karlsruhe, West Germany,1983,(2):1019-1022.
[6]钱慧敏,等,基于各向异性扩散的几种平滑算法比较及改进[J],南京理工大学学报,2007,31(5):606-610 .
[7]P.Perona, and J.Malik. Scale-space and edge detection using an-isotropicdiffusion[J]. IEEE Trans Pattern Anal Machine Intel, 1990,12(7):629-639.
[8]F.Catte, P.L.Lions, J.M.Morel, and T.Coll. Image Selective Smoothing and Edge Detectionby Nonlinear Diffusion[J]. SIAMJournal on Numerical Analysis,1992,29(1):182-193.
[9]J.Weickert. Anisotropic Diffusion in Image Processing[Z]. University of Copenhagen Denmark Press, 1998.
[责任编辑:邓丽丽]
