基于遗传算法的IMX系统测试数据自动生成研究

冯 霞 郝慧敏



基于遗传算法的IMX系统测试数据自动生成研究

冯 霞①②郝慧敏*①

①(中国民航大学计算机科学与技术学院 天津 300300)②(中国民航大学中国民航信息技术科研基地 天津 300300)

利用遗传算法进行测试数据自动生成是近年来的研究热点，其有效性高度依赖于适应度函数的选取和初始种群的筛选。该文探索将遗传算法应用到IMX(Integrated Management X-software)系统测试数据自动生成以提高其回归测试的质量，将IMX系统专业测试人员手动生成的测试数据作为基础测试数据，并提出一种基于测试路径对目标路径覆盖率的初始种群筛选标准。在三角形程序和IMX系统平台上的实验表明，所提方法在寻找测试数据时所用的时间和迭代次数较少，且生成的测试数据具有较好的多样性。

测试数据自动生成；遗传算法；初始种群筛选；适应度函数；IMX系统

1 引言

IMX(Integrated Management X-software)系统是一套用于管理航空公司运行质量和安全审计的软件，系统的研发能够帮助航空公司提升运营质量和安全性能。IMX系统开发周期非常短，每隔一周就需要提交一个新版本，更新速度极快，因而对回归测试的频度和效率要求极高。这就要求开发团队采取边开发边测试的策略，在频繁修改代码的同时完成测试工作。

遗传算法是一种通过模拟自然进化过程搜索最优解的智能算法，近年来利用遗传算法实现高效测试数据自动生成，进而提高回归测试效率的研究越来越受到关注。文献[1]为提高测试效率，利用遗传算法生成大量测试数据进行测试覆盖，保证了较高的测试故障覆盖率[2]。文献[3]将遗传算法应用在复杂、多条件约束的软件系统中，解决手工生成测试数据效率低下问题。文献[4]在遗传算法的基础上动态地将稀有数据扑捉，调整权重增加稀有数据的适应值，进而提高测试数据的生成效率。

考虑到不同初始种群和适应度函数对算法有效性会产生直接影响[5]，文献[6]针对并行程序利用基于合作式的协同进化遗传算法实现覆盖目标路径的测试数据自动生成，并对子种群和合并种群采用不同的适应度函数评估。文献[7]通过对基本适应度函数的修正，采用自适应适应度函数避免了遗传算法陷入早熟现象，提高了算法的搜索能力。文献[8]采用遗传算法生成回归测试所需数据，通过计算测试路径与目标路径的相似度来筛选初始种群，利用已有测试数据所含有利信息来优化种群，提高遗传算法的运行效率。

总结以上研究，现有学者在利用遗传算法实现测试数据自动生成时仍需解决的主要问题有：(1)针对不同的应用，学者们提出了不同的适应度函数，可见适应度函数是高度依赖于数据集的。针对某一特定系统，如何选择合适的适应度函数仍然值得研究；(2)有效利用初始数据的有用信息可以提高算法的效率，如何针对测试的需求及数据集自身的特点，进而设定合理的筛选标准来更好地优化数据，是另一个值得研究的问题。

本文研究遗传算法在IMX系统测试数据自动生成中的应用，主要贡献为：(1)将IMX系统专业测试人员手动生成的测试数据作为基础测试数据，有效利用了IMX测试人员的丰富经验。(2)提出一种基于路径覆盖率的初始种群筛选标准，在三角形程序和IMX系统程序中进行实验，有效验证了该方法在较少时间和迭代次数内即可实现测试数据的自动生成。(3)针对IMX系统选择出有效的适应度函数计算方法，即分支距离与层接近度之和。

2 基于遗传算法的测试数据生成

2.1 问题分析

遗传算法是一种结合了生物学中自然选择和遗传学中生物进化的计算模型，可应用在数学中以解决最优化问题，最初由美国Michigan大学Holland教授于1975年首次提出。由于遗传算法搜索最优解的求解空间和自动测试数据生成的问题空间模型相似，所以越来越多的学者将遗传算法用作测试数据自动生成来提高回归测试的效率。

本文旨在研究IMX系统中基于遗传算法的单目标路径测试数据生成问题。该问题可描述为：

(1)选取IMX系统中的一个核心程序；

采用遗传算法解决IMX系统测试数据自动生成，需要将问题建模成最优化问题。

将测试数据代入到程序中运行得出的路径称为测试路径，这里把测试路径与目标路径的接近程度作为该测试路径的适应度，记为,。根据适应度函数，就可以为测试数据自动生成问题建立式(1)，式(2)最小化或最大化模型：

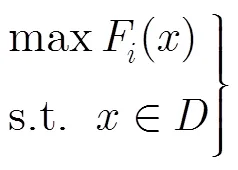
2.2初始种群筛选

利用遗传算法实现测试数据自动生成时，初始种群的不同设定对算法性能产生极大影响，利用有效的筛选标准来优化初始种群，可以增强算法的搜索能力，从而提高测试数据自动生成的效能。

2.2.1初始种群与算法性能 遗传算法的种群是一代一代演化的，且当前代的个体仅与上一代个体相关，与其之前所有个体无关[9]。遗传算法的这一特征可用定义1描述。

文献[10,11]在论述初始种群与遗传算法性能关系时，给出了定义2和定理1：

定理1说明交叉算子可搜索到包含当代种群中极小模式的所有个体，但无法搜索到不在极小模式中的全部个体。定理1反应了交叉算子的搜索能力，同时表明，初始种群对交叉算子的搜索能力具有较强的决定性作用[12]；而遗传算法的收敛速度依赖于交叉操作。由此可见，初始种群选择对遗传算法的收敛性能非常关键，且在实际应用中，不合理的初始种群选择，会增加算法的迭代次数，甚至会使搜索结果陷入局部最优，降低算法性能。

综上，通过选用有效筛选标准，选取充分表征解空间个体信息的初始种群，就可增加交叉算子的搜索能力，进而减少进化代数和收敛时间，提高算法性能。

2.2.2筛选标准 利用一定的筛选标准对回归测试中已有测试数据进行筛选，可以充分利用已有测试数据所含有用信息，从而提高测试数据生成的效率[13]。但不同的筛选标准，生成的测试数据效能差异很大，因此研究选择适用于IMX系统的筛选标准对系统的测试非常重要。

IMX系统是基于白盒测试中的路径覆盖展开的测试，好的测试数据应该覆盖到尽可能多的节点路径，因此本文提出根据路径的覆盖率来筛选初始种群。

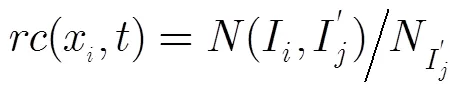
按式(3)计算每个测试数据的路径覆盖率，并将其求和后计算均值得出测试数据的平均路径覆盖率，将大于或等于平均路径覆盖率的所有个体筛选出来，作为初始种群的部分个体，若筛选出的个体数量不足于预定义的初始种群数量，则其余个体将在被测程序所对应的输入域范围内随机产生[8]。即满足式(4)：

2.3适应度函数选择

针对IMX系统，本文分析比较了如下4种不同适应度计算方法。

(1)分支距离+层接近度(方法1) 利用文献[14]和文献[15]提出的适应度函数设计，即适应度函数为分支距离与层接近度的两者之和，且分支距离是被规范到(0,1)之间的一个数，这样有效降低了分支距离和层接近度之间的落差。该方法中的适应度值越小，表示越接近目标路径，因此应该选取适应度值较小的个体作为后续迭代的数据。

(2)分支距离(方法2) 对分支距离的计算，文献[16]提出了一种新的设计方法，其基本设计思想是将初始的分支距离除以自身与常数的和(常数大于0)。将该分支距离作为适应度函数时表示为

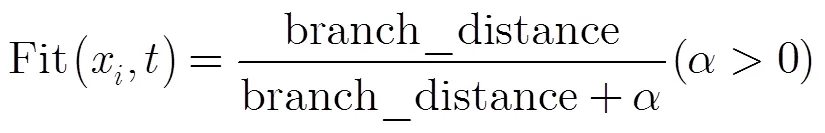
(3)层接近度(方法3) 对于层接近度方法的计算也有多种，本文采用文献[5]中提到的计算方法，即统计测试路径未覆盖目标路径的节点的个数，记作，将该值除以目标路径的节点的个数。将其作为适应度函数，则计算公式为

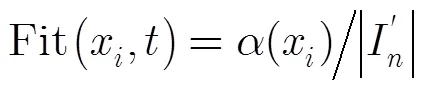
(4)拟合度(方法4) 采用测试路径与目标路径的拟合度作为适应度函数。将测试路径和目标路径按节点序列匹配的方法计算出的子路径记为。计算公式如式(7)[6,17]：

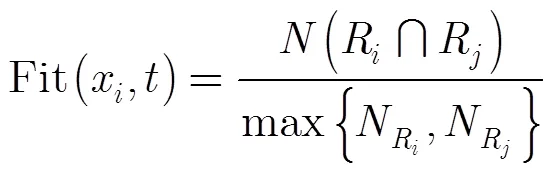
2.4 算法步骤

根据以上研究，利用遗传算法实现测试数据自动生成的步骤如下：

(1)初始化所有参数；

(2)根据一定筛选标准对基础数据进行选择，将满足标准的数据作为初始种群；

(3)判断是否满足算法停止条件，是则算法停止并输出结果，否则执行步骤(4)；

(4)采用轮盘赌方法对初始种群进行选择操作；

(5)对上述选择出的个体进行单点交叉操作；

(6)将未覆盖目标路径的节点对应的输入变量进行变异操作；

(7)是否满足最大(最小)适应度函数或最大迭代次数，是则输出结果，否则继续迭代。

3 实验

3.1 IMX系统被测程序

对于IMX系统，所选的被测程序为审计(audit)模块中的审计状态(audit)变化过程，即航空公司在进行审计时，根据符合项和不符合项的状态，审计状态发生相应变化的流程。其中，审计状态包括SCHEDULED, CONDUCTED, READY FOR CLOSURE, CLOSED。

表1 测试数据信息

audit的各个状态转换如图1所示。

图1 audit状态转换

程序修改条件语句由if(findingQty<= unconformityQty||findingOKQty

3.2 三角形程序

三角形程序主要功能是根据三条边的大小来判断三角形所属类别。程序修改条件语句由if((a= =b) ||(a==c)||(b==c))变为if((a==b && b!=c)||(a==c && c!=b)||(b==c && a!=c))，因此，所选取的目标路径应包含修改节点，目标路径为：三角形类别是等腰三角形。

3.3实验参数设置

在利用遗传算法生成测试数据时，采用ASCII码编码，轮盘赌选择策略，并采用单点交叉(Pc=0.8)和单点变异(Pm=0.2)，实验中最大迭代次数均为1000次，运行次数均为20。

初始种群规模与算法解空间大小相关，且直接影响到遗传算法的收敛性或计算效率。种群规模过小，则易早熟，从而过早收敛；过大则会耗费大量的资源，代价增高。通常，可根据实际情况在10~200之间选定[18]，也可选取4~6个，其中为被测程序中参数的个数[19]。

为确定初始种群规模的大小，本文分别选取种群规模为10,20,40,50,80,160, 在IMX系统上进行了实验验证。

种群规模(P)与收敛时间(T)和收敛代数(GEN)关系如图2，图3所示。

图2表明随着种群不断增多，算法的收敛时间逐渐增大，当种群规模为40到80之间时，时间先减小，随后又呈上升趋势。由图3可知，算法的收敛代数会随着初始种群规模的不断增加而逐渐降低，最后趋于平缓。可见，选择过小或过大的种群规模会降低算法的性能[5]。因此，针对IMX系统，本文选择初始种群规模为50。

3.4不同筛选标准实验

3.4.1 IMX系统程序 将本文2.2节的路径覆盖率筛选标准、文献[8]中相似度筛选标准以及传统方法三者进行比较。其中，传统方法是指在利用遗传算法生成测试数据时，对已有的测试数据随机选择作为算法的初始种群，并未充分利用基础数据含有的有用信息。

算法停止条件为满足设定的适应度值和最大迭代次数。本次实验中选取层接近度与分支距离结合作为遗传算法的适应度函数。不同筛选标准实验结果如表2所示。

图2 收敛时间和种群规模关系 图3 收敛代数均值和种群规模关系

表2初始数据数量为50的筛选标准比较

实验次数路径覆盖率筛选标准相似度筛选标准传统方法 1(READY_FOR, 150, 45, 74, 50, 29)(READY_FOR, 90, 30, 20, 11, 7)(READY_FOR, 12, 2, 4, 2, 2)(READY_FOR, 84, 0, 23, 20, 14) 2(READY_FOR, 50, 10, 23, 0, 0)(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR, 28, 0, 5, 5, 1) 3(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 23, 1, 5, 3, 2) 4(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR, 76, 9, 29, 22, 0) 5(READY_FOR, 50, 40, 5, 4, 3)(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR, 51, 15, 17, 6, 4) 6(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 75, 32, 42, 26, 16) 7(READY_FOR, 41, 2, 22, 10, 2)(READY_FOR, 50, 40, 5, 4, 4)(READY_FOR, 41, 2, 22, 10, 2) 8(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR,50, 40, 10, 9, 9)(READY_FOR, 50, 23, 19, 10, 3) 9(READY_FOR, 86, 28, 43, 31, 20)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 43, 1, 9, 7, 1) 10(READY_FOR, 50, 10, 17, 0, 0)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 70, 35, 35, 35, 25) 11(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 54, 11, 10, 8, 8) 12(READY_FOR, 90, 30, 54, 14, 9)(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 86, 28, 43, 31, 21) 13(READY_FOR, 80, 37, 37, 31, 15)(READY_FOR, 90, 30, 58, 37, 20)(READY_FOR, 50, 10, 18, 0, 0)(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR, 92, 24, 19, 10, 1) 14(READY_FOR, 23, 1, 5, 3, 1)(READY_FOR, 80, 20, 56, 31, 6)(READY_FOR, 54, 30, 23, 19, 19) 15(READY_FOR, 54, 30, 23, 19, 19)(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR, 80, 37, 37, 31, 15) 16(READY_FOR, 50, 40, 7, 6, 0)(READY_FOR, 50, 40, 9, 5, 2)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 39, 0, 8, 8, 7) 17(READY_FOR, 48, 20, 22, 19, 3)(READY_FOR, 150, 45, 102, 20, 5)(READY_FOR, 65, 22, 30, 26, 26) 18(READY_FOR, 50, 40, 10, 9, 9)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 36, 13, 22, 22, 14) 19(READY_FOR, 50, 40, 6, 6, 3)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 29, 1, 21, 13, 6) 20(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 12, 2, 10, 9, 9)(READY_FOR, 86, 46, 35, 24, 23) 时间均值(s)0.1620.1660.321 迭代均值(次)4.4004.700211.150

通过上述实验可以看出：(1)传统的遗传算法需要消耗0.321 s，迭代211.150次才可找到测试数据。可见传统遗传算法的效率较为低下。(2)相似度方法和路径覆盖率方法在时间和迭代次数上相差不多，且该值远远小于传统方法对应值。但是通过相似度方法筛选的测试数据失去了多样性，找到相同数据次数较多，而路径覆盖率方法提高了测试数据的多样性。(3)随着测试数据的增多，利用路径覆盖率筛选标准生成测试数据时所需的时间和迭代次数将均少于相似度方法，本文方法的优势逐渐凸显。

3.4.2三角形程序实验设置 为验证2.2节所提方法的可靠性和普遍性，同时将其应用在对三角形程序的测试上。由于是回归测试，所以已经具有一些可以覆盖原来三角形程序所对应目标路径的测试数据。对于传统方法，是随机选取已有的测试数据作为算法的初始种群，对于路径覆盖率筛选标准和相似度筛选标准来说，则是分别利用对应筛选标准选取符合要求的数据作为初始种群的一部分，其余个体则是在输入域内随机产生。

适应度函数选用层接近度与分支距离之和计算。实验结果如表3所示。

表3三角形程序实验比较

评价指标路径覆盖率筛选标准相似度筛选标准传统方法 时间均值(s)0.4750.8171.032 迭代均值(次)57.800448.600660.850

由以上实验可知，本文方法所用的时间和迭代次数均为最小，且在100次以内就可找到覆盖目标路径的测试数据，效率极高。而相似度筛选标准方法和传统方法，需消耗很多时间和迭代次数，且存在找不到覆盖目标路径测试数据的现象。由此足以证明本文方法的有效性。

3.5 不同适应度函数实验

采用2.3节中介绍的方法应用在IMX系统上进行对比。以路径覆盖率准则对初始种群进行筛选。实验结果如表4所示。

表4不同适应度函数性能比较

评价指标方法1方法2方法3方法4 时间均值(s)0.1620.4140.3152.439 迭代均值(次)4.70038.20020.600754.400

由上实验得出，在利用遗传算法进行测试数据生成时，选取不同的适应度函数指标对数据生成的效率有很大影响。对于IMX系统来说，方法4所需时间是方法1的15倍之多，且迭代次数也远远超过了方法1，效率非常低下。方法2和方法3相对于方法4，效率得到了很大提高，但迭代过程中每次都会产生大量的覆盖率为0.0%的无用数据。采用方法1时需要最少的时间和迭代次数，且产生的测试数据具有较好的多样性，多数数据的覆盖率都能达到90.0%以上，大大增强了测试的效率。由此可知，对于IMX系统，应将分支距离与层接近度之和作为遗传过程中适应度函数的评价指标。

4 结束语

为提高对IMX系统的测试效率，本文采用遗传算法实现回归测试中测试数据的自动生成。针对不同的初始种群筛选标准和适应度函数对测试数据有效性的影响进行了研究，并提出了路径覆盖率筛选标准，在IMX系统核心程序和三角形类别判定程序中的实验表明，本文方法在生成测试数据时所需时间和迭代次数均较少。进而又通过对多种不同适应度函数计算方法的比较实验，选取了分支距离与层接近度之和作为IMX系统的适应度度量方法。

[1] Swain S and Mohapatra D P. Genetic Algorithm-Based Approach for Adequate Test Data Generation[M]. India: Intelligent Computing, Networking, and Informatics, Springer, 2014: 453-462.

[2] 邝继顺, 刘杰镗, 张亮. 基于镜像对称参考切片的多扫描链测试数据压缩方法[J]. 电子与信息学报, 2015, 37(6): 1513-1519.

Kuang Ji-shun, Liu Jie-tang, and Zhang Liang. Test data compression method for multiple scan chain based on mirror-symmetrical reference slices[J].&, 2015, 37(6): 1513-1519.

[3] Michael C C, McGraw G E, Schatz M A,.. Genetic algorithms for dynamic test data generation[C]. Proceedings of the 12th IEEE International Conference on Automated Software Engineering, 1997: 307-308.

[4] 张岩, 巩敦卫. 基于稀有数据扑捉的路径覆盖测试数据进化生成方法[J]. 计算机学报, 2013, 36(12): 2429-2440.

Zhang Yan and Gong Dun-wei. Evolutionary generation of test data for paths coverage based on scarce data capturing[J]., 2013, 36(12): 2429-2440.

[5] 刘向辉, 韩文报, 权建. 基于遗传策略的格基约化算法[J]. 电子与信息学报, 2013, 35(8): 1940-1945.

Liu Xiang-hui, Han Wen-bao, and Quan Jian. A new lattice reduction algorithm based on genetic strategy[J].&, 2013, 35(8): 1940-1945.

[6] Tian T and Gong D. Test data generation for path coverage of message-passing parallel programs based on co-evolutionary genetic algorithms[J]., 2014, 22(79): 1-32.

[7] 严韬, 陈建文, 鲍拯. 基于改进遗传算法的天波超视距雷达二维阵列稀疏优化设计[J]. 电子与信息学报, 2014, 36(12): 3014-3020.

Yan Tao, Chen Jian-wen, and Bao Zheng. Optimization design of sparse 2-D arrays for Over-The-Horizon Readar (OTHR) based on improved genetic algorithm[J].&, 2014, 36(12): 3014-3020.

[8] 巩敦卫, 任丽娜. 回归测试数据进化生成[J] . 计算机学报, 2014, 37(3): 489-499.

Gong Dun-wei and Ren Li-na. Evolutionary genetation of regression test data[J]., 2014, 37(3): 489-499.

[9] 曹凯, 陈国虎, 江桦, 等. 自适应引导进化遗传算法[J]. 电子与信息学报, 2014, 36(8): 1884-1890.

Cao Kai, Chen Guo-hu, Jiang Hua,. Guided self-adaptive evolutionary genetic algorithm[J].&, 2014, 36(8): 1884-1890.

[10] 徐宗本, 高勇. 遗传算法过早收敛现象的特征分析及其预防[J]. 中国科学: E 辑, 1996, 26(4): 364-375.

Xu Zong-ben and Gao Yong. The analysis and prevention of genetic algorithm premature convergence[J].(), 1996, 26(4): 364-375.

[11] Suzuki J. A Markov chain analysis on simple genetic algorithms[J]., 1995, 25(4): 655-659.

[12] 何大阔, 王福利, 贾明兴. 遗传算法初始种群与操作参数的均匀设计[J]. 东北大学学报: 自然科学版, 2005, 26(9): 828-831.

He Da-kuo, Wang Fu-li, and Jia Ming-xing. Uniform design of initial population and operation parameters of genetic algorithm[J].(), 2005, 26(9): 828-831.

[13] Xuan J and Monperrus M. Test case purification for improving fault localization[C]. FSE 2014 Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering, New York, NY, USA, 2014: 52-63.

[14] McMinn P. Evolutionary search for test data in the presence of state behaviour[D]. [Master dissertation], University of Sheffield, 2005: 1-242.

[15] Harman M and McMinn P. A theoretical and empirical study of search-based testing: local, global, and hybrid search[J]., 2010, 36(2): 226-247.

[16] Arcuri A. It does matter how you normalise the branch distance in search based software testing[C]. Proceedings of the 3rd International Conference on Software Testing, Verification and Validation, Pairs, France, 2010: 205-214.

[17] Xie X Y, Xu B W, Shi L,.. Genetic test case generation for path-oriented testing[J]., 2009, 20(12): 3117-3136.

[18] 雷英杰, 等. MATLAB 遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2005: 60-61.

Lei Ying-jie,.. Application of Genetic Algorithm ToolBox Based on MATLAB[M]. Xian: Xidian University Publisher, 2005: 60-61.

[19] 刘晓霞. 种群规模对遗传算法性能影响的研究[D]. [硕士论文], 华北电力大学, 2010: 1-37.

Liu Xiao-xia. A research on population aize impaction on the performance of genetic algorithm[D]. [Master dissertation], North China Electric Power University, 2010: 1-37.

Research on Automatic Generation of Test Data in MX Based on Genetic Algorithms

Feng Xia①②Hao Hui-min①

①(,,300300,)②(,,300300,)

Using genetic algorithms to generate test data automatically is becoming a hot topic in recent years, the method on effectively generating data is highly dependent on choosing the proper fitness function and the selecting standard. The genetic algorithm is used on Integrated Management X-software (IMX) system to help it improve the quality of regression test. Those basic test data used in this paper are taken from the data that generated by professional testers in IMX, and an initial population selecting standard is proposed based on the coverage. Experiments on IMX and triangle program show that the proposed algorithm is more effective than others, for example, with less time and iteration the method can find the testing data correctly, especially on data variety.

Test data generation; Genetic algorithm; Initial population selecting; Fitness function; Integrated Management X-software (IMX) system

TP311

A

1009-5896(2015)10-2501-07

10.11999/JEIT150291

2015-03-09；改回日期：2015-06-15；

2015-07-27

郝慧敏 1048866836@qq.com

国际航空运输协会(IATA)项目(70003418)和国家科技支撑计划(2014BAJ04B02)

The International Air Transport Association Fund (70003418); The National Key Technology Research and Development Program of the Ministry of Science and Technology of China (2014BAJ04B02)

冯 霞： 女，1970年生，教授，博士，主要研究方向为数据挖掘和民航智能信息处理研究.

郝慧敏： 女，1990年生，硕士生，研究方向为数据挖掘和民航智能信息处理研究.