基于非平稳时序ARIMA模型的W频段雨衰预测

杨 峰 薛 斌 刘 剑



基于非平稳时序ARIMA模型的W频段雨衰预测

杨 峰 薛 斌*刘 剑

(空军工程大学信息与导航学院 西安 710077)

针对目前绝大多数雨衰预测模型仅验证到55 GHz，而经过验证的W频段预测模型相对较少，且存在模型表述复杂度高、计算量大的问题，该文提出一种结构简单、计算量小的实时预测方法。该方法基于ARIMA模型，利用非平稳雨衰时序中相邻时序间的相关性建立预测模型，对初始序列进行平稳性检验，通过差分变换将非平稳序列转化为平稳序列，并对平稳化后的时间序列进行参数估计及诊断检验，将传统非线性预测转化为线性预测。并先将该ARIMA(1,1,6)模型在不同极化方式、预测间隔和时序个数的条件下进行比较，然后分别与ITU-R, Silva Mello模型在垂直极化、预测间隔0.10 GHz，时序个数50的条件下进行比较，最后使用ARIMA(1,1,6)模型进行预测，并对照预测序列与仿真序列的吻合度。结果表明，ARIMA模型与ITU-R, Silva Mello模型所得结果预测误差不超过，且衰减变化趋势基本相同，预测序列与仿真序列间吻合度较高，说明该方法可用于W频段雨衰预测，且预测精度高，模型表述简单。

雨衰预测；W频段；非平稳时间序列；ARIMA；差分

1 引言

卫星通信已成为全球通信的重要组成部分，近年来，随着宽带多媒体卫星通信的蓬勃发展，C, Ku, Ka等较低频段频带资源日益紧张。为了满足卫星系统对通信容量和传输速率日益增长的需求，各国加强了对更高频段的研究，如Q/V频段和W频段，目前W频段已经成为卫星通信研究前沿[1]。美国，意大利等国已率先对W频段卫星通信予以重点研究[1,2]。国际电信联盟(International Telecommu- nication Union, ITU)为W频段卫星通信分配的频段是：上行81~86 GHz，下行71~76 GHz。与其他较低频段相比，该频段可用带宽大，传输速率高，天线尺寸小，波束窄，抗干扰能力强[3,4]，受到了各国广泛重视。但与此同时它也存在一些问题，如由大气吸收、雨衰、快衰落、反射等引起的恶劣的信道传播特性[5]，非线性失真、相位噪声等严重的硬件问题[6]。其中降雨是影响通信质量最严重的大气因素之一(数据体现，与其他频段相比较)，所以，准确预测降雨衰减对W频段卫星通信系统设计和保障卫星链路质量至关重要。

目前国际上雨衰预测模型很多，如Crane Global模型、Assis-Einloft Improved模型、Silva Mello模型[7]、ITU-R 模型[8]、DAH模型和UK模型等。文献[9]基于指数雨胞分布模型，提出了一种地面视距链路的全概率雨衰预测模型。利用ITU-R视距链路数据库数据回归得到了路径调整因子中的参数，提高了预测精度，但对物理基础要求较高，计算量较大；文献[10]基于SC EXCELL模型，利用合适的测量数据作为输入，如月降雨高度、降雨速率、降雨分布等，对预测流程作了详尽的介绍，并将年统计数据得到的精确度与月统计数据得到的精确度进行比较，月精确度较高，但是对物理基础要求较高，且对不同频率雨衰变换对时间间隔要求较大，不同天气要采取不同的采样时间间隔，在实际应用过程中不易把握。文献[11]基于微波雨衰的幂律关系，采用层析技术建立了2维降雨场反演模型，能够提供高时空分辨率的2维降雨强度分布，提高了反演精度，但处理层析技术时对雨衰模型呈非线性频段处理采用了线性化的处理方法，反演误差较大。通过这些模型可以获得雨衰的长期统计特性，但降雨及其产生的雨衰是不平稳的，很难精确预测短期(如下一分钟)降雨衰减，不利于实时要求较强的业务。

在此基础上，本文采用时间序列分析法，对降雨产生的雨衰时间序列间的相关性进行研究，提出一种基于非平稳时序ARIMA模型的W 频段雨衰实时预测方法。本文选取罗马地区降雨数据进行验证，将ARIMA模型与在W频段经过验证的ITU-R和Silva Mello雨衰预测模型进行比较来验证该方法的有效性。

2 时间序列分析法和ARIMA模型

上述传统雨衰预测模型均基于对各类参数的计算基础上，并未考虑数据之间的内部关联性，且绝大多数模型仅验证到55 GHz，在W频段进行有效雨衰预测经过验证的模型目前仅为少数，如ITU-R模型和Silva Mello模型。本文采用时间序列分析法对W频段雨衰进行预测，并与ITU-R, Silva Mello模型预测结果进行比较。

2.1时间序列分析法

时间序列分析法[12]是利用按时间顺序排列的一组数列，应用数理统计方法对序列内部的相互关系进行处理，以预测事物未来发展情况。其中，平稳时间序列的均值、方差、协方差等统计特性并不随时间推移而变化，且这些数字特征具有遍历性(能够保证样本统计量是总体参数的一致估计)，在不同时点上呈现出相似的规律性，便于根据序列在过去的特征规律，建立拟合模型，对未来趋势加以预测。

而在实际降雨衰减过程中，很多序列是不平稳的[13]，其均值、方差和自协方差等数字特征会随时间推移而变化，也就是在不同时点上的统计规律不同，且不具有遍历性，所以不能直接利用此类序列的以往信息来预测未来的可能情景，需要采用一些方法将非平稳序列变换为平稳序列。而差分可以从缓慢的长期变化中，分离出微小的、快速的变化因素，可以将非平稳序列处理为平稳序列，特别适合处理此类问题[14]。因此本文采用ARIMA模型来研究雨衰时间序列间的相关性，以此预测未来雨衰情况。

2.2 ARIMA模型

自回归移动平均(Auto Regression Moving Average, ARMA)模型[15]广泛应用于物理科学、经济学、生物学等领域随机现象的预测，非常适合于预测平稳时间序列。假设是一组有效的平稳时间序列，则的ARMA(,)模型可表示为

ARIMA模型[15]是对ARMA模型进行优化得来的，属于线性模型，适合于预测非平稳时间序列。在实际降雨中，绝大多数雨衰时间序列是不平稳的，在预测前需采用一些方法将非平稳序列变换为平稳序列，如差分处理。假设是一组非平稳时间序列，则的ARIMA(,,)模型可表示为

图1为构建ARIMA模型的流程，包括以下几步：平稳性检验、模型识别、参数估计、诊断验证和预测分析。本文结合罗马地区降雨数据，进行建模，并将该ARIMA(1,1,6)模型在不同极化方式、预测间隔和时序个数的条件下进行比较，然后分别与ITU-R, Silva Mello模型进行比较。

图1 ARIMA模型构建流程

3 ARIMA模型构建

3.1平稳性检验

本文采用罗马地区降雨数据。使用文献[16]中的方法及SPSS(Statistical Product Service Solutions)统计软件得到罗马地区71.9~76.8 GHz处雨衰仿真时间序列图，如图2(a)所示。

采用自相关函数ACF来验证时间序列的平稳性。统计学家给出了许多关于自相关函数的估计方法，并得出结论，延迟的自相关函数最令人满意的估计是

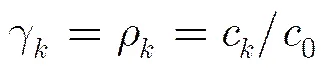
采用SPSS软件求解该序列的自相关函数ACF。若其自相关函数ACF迅速减小到零，则满足平稳性条件。图2(b)为使用SPSS软件得到的初始雨衰时间序列的ACF。

由图2(b)可看出，初始雨衰时间序列的ACF没有迅速减小为零，说明该序列非平稳，需对其进行差分处理，使其平稳化。图3(a)和图3(b)分别为一阶差分后的雨衰时间序列及其ACF。

由图3(b)可知，经一阶差分的雨衰时间序列的ACF迅速减小为零，说明该序列被平稳化，且差分阶数=1。

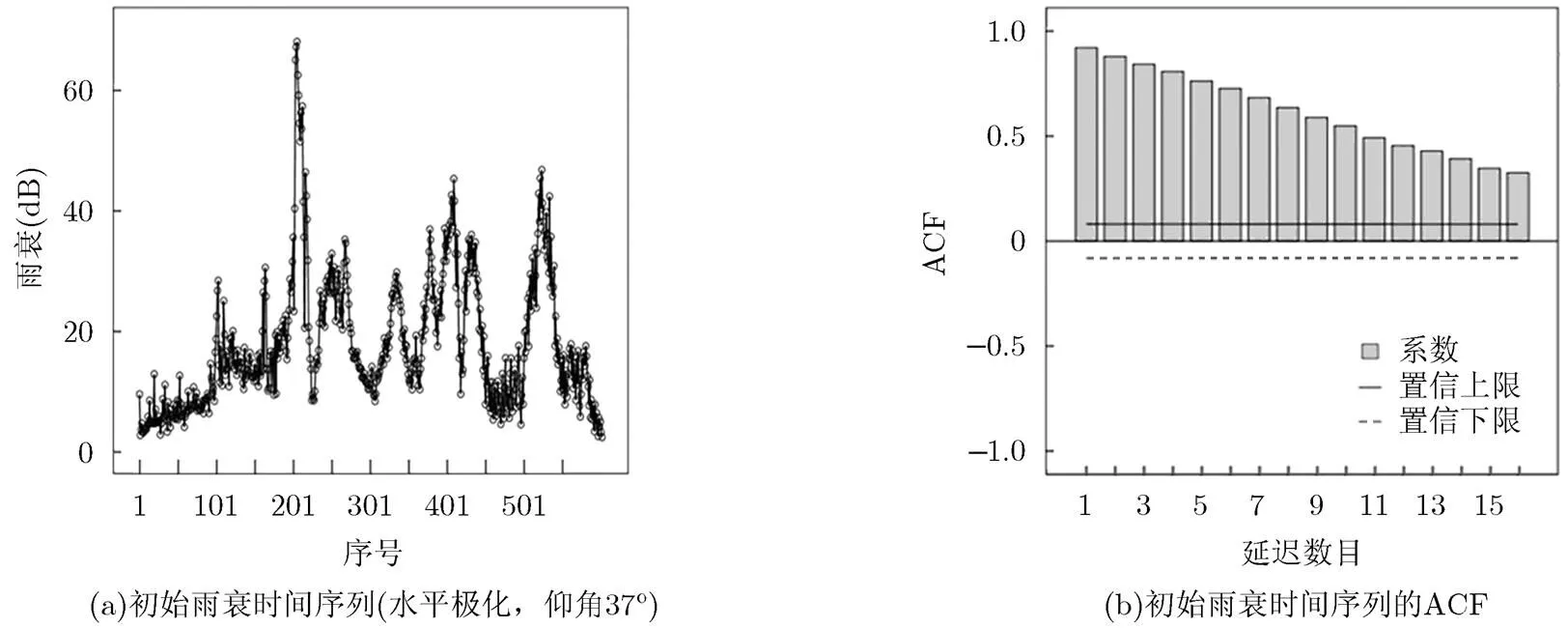
图2 初始雨衰时间序列及其ACF

图3 差分雨衰时间序列及其ACF

3.2模型识别

检验平稳性和确定差分阶数之后，使用自相关函数ACF和偏自相关函数PACF确定和的值，即确定ARIMA(,,)模型结构。图4为一阶差分后的平稳雨衰时间序列的抽象模型示意图。

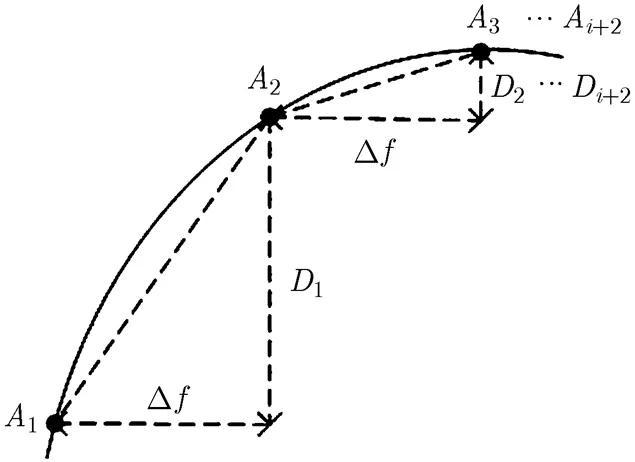
图4 平稳雨衰时间序列抽象模型示意图

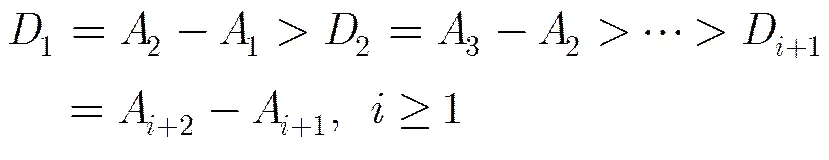
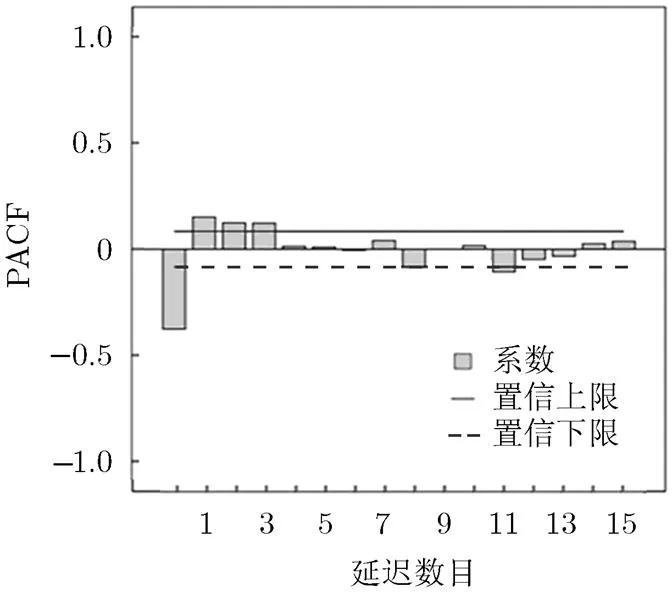
图5 差分雨衰时间序列的PACF

3.3参数估计

在3.1节中对平稳性进行了检验，从检验结果可以看出式(5)能够使用。要想得到的估计值，就得先求出和的值。可使用最小均方估计、最小方差法、点估计或使用ACF直接估计ARIMA模型的参数。本文采用最小方差法进行计算，即选使均方偏差最小。

表1 ARIMA(1,1,6)的参数和

表1 ARIMA(1,1,6)的参数和

参数日期 2010年3月14日2010年3月29日2010年4月14日2010年5月13日 -0.8539-0.2116-0.9939 0.7422 -0.5715-0.4952 0.1541 1.0027 0.3768 0.3945-0.7961 0.0884 0.1358 0.2459 0.3441-0.0837 -0.0230 0.0059 0.1900-0.0686 -0.0613 0.0124 0.0641 0.3431 0.0191-0.0110 0.1349 0.1748

3.4诊断检验

可通过预测时间序列与真实序列间残差序列的ACF和PACF，来确认该模型是否合适。

求解上述预测差分时间序列与真实序列间残差序列的ACF和PACF，可知，ACF和PACF迅速减小为零，表明该残差序列与白噪声序列相似，可确认ARIMA(1,1,6)模型对罗马地区该样本中雨衰测量时间序列是可行的。并得出以下结论：初始雨衰时间序列不平稳；经差分的雨衰时间序列在差分阶数=1时是平稳的；=1,=6可行。也就是说，ARIMA(1,1,6)模型可用于预测W频段雨衰时间序列。得到的ARIMA(1,1,6)模型为

3.5 预测分析

误差是不确定性最直观的表现形式，预测结果的不确定性可由预测误差的变化趋势很好地展现出来。该模型通过控制不同的极化方式、预测间隔和时序个数，与ITU-R模型的预测精度进行比较，验证本方法的有效性、参数计算简单和高预测精度。

4 仿真分析

4.1 不同极化方式下的预测精度

从图6(a)可以看出，分别采用水平极化、圆极化和垂直极化这几种不同的方式进行预测，三者得到的预测精度之间的差别并不是很明显，与此同时随频率的增大，三者的预测精度会逐渐朝同一程度趋近。由图6(a)可知，在71.0~76.6 GHz范围内，垂直极化和圆极化方式下预测精度差别较小，在76.6 ~86.0 GHz范围内，水平极化和垂直极化方式下的误差大致相同，但在整个W频段范围内，三者间预测精度差异很小，所以基本上可以忽略极化方式对该模型参数的影响，同时也可简化该模型在不同极化方式下的预测计算量，降低了复杂度。

4.2不同预测间隔下的预测精度

选择一阶差分ARIMA(1,1,6)模型，采用垂直极化方式，时间序列个数，图6(b)为仿真结果。由图6(b)可以看出，不同预测间隔下，ARIMA(1,1,6)模型的预测值间的误差随频率增大而升高，该结论与之前对平稳性的验证中得出的结论是相符合的，这说明所采用的算法及进行的仿真都是可取的；频率预测间隔不同则预测模型的预测精度就会不同，因为降低频率预测间隔，将会增强前导雨衰数据之间的相关性，而差分是线性变换，线性变换提高了数据之间的相互联系，所以将增强时间序列中各元素之间的相关性，从而可以提高预测精度，更精确地估计模型参数；而且预测某一频段范围的降雨衰减值时，频率预测间隔大小与预测数之间的关系比较密切，预测数的多少由频率预测间隔的大小来决定，从而导致会生成不同的累积误差，且随着预测间隔的增大生成的累积误差会减小，因此当预测间隔为0.20 GHz时曲线的变化趋势比较显著，在71.0~75.2 GHz范围内，预测间隔为0.10 GHz与0.05 GHz时两者间预测精度差别较小；在75.2~86.0 GHz范围内，预测间隔为0.20 GHz与0.05 GHz时两者间预测精度的差别较小，同时随频率的增大两者的预测精度会逐渐朝同一程度逼近。

表2模型参数

时序个数n预测间隔(GHz)偏相关系数 200.20 0.6539-0.0347-0.00780.02700.0463 0.10 0.0621 0.0717 0.08140.07260.1855 500.05-2.6132-1.5761 1.70032.54640.9676 0.10 0.8236 0.0427 0.05690.06310.1849 0.7923 0.0376 0.04850.06260.1763 0.8932 0.0016 800.10 0.0050 0.0057 0.00640.00730.0078 0.6835 0.0267 0.01570.00810.0052 0.8478 0.0593 0.06500.15790.0796 0.0083 0.0086 0.00890.07020.0815

图6 不同极化方式和预测间隔的预测误差比较

4.3不同时序个数下的预测精度

选择一阶差分ARIMA(1,1,6)模型，采用垂直极化方式，频率预测间隔为0.10 GHz，图7(a)为仿真结果。由图7(a)可以看出，时间序列个数不同则预测模型的预测精度也会有所差异，原因是前导雨衰数据量的多少决定了时间序列个数，前导雨衰数据描述了降雨数据和雨衰数据的部分特性，它的数据越多，对数据的描述就会越充分，就越能准确地估计数据间的相关程度，从而越能精确地估计模型参数；同时注意到待计算模型参数的多少由时间序列个数的多少来确定，从而导致产生不同的累积误差，累积误差会随着时间序列数目的增多而增大，所以时间序列个数为80时误差曲线的趋势变化较为明显，在71~75 GHz内，时序个数为80与50时两者预测误差曲线基本吻合；在75~79 GHz内，时序个数为50和20时两者间预测精度的差别较小；在79~86 GHz内，时序个数为80与20时两者间预测精度较为接近，且误差较小，与此同时随着预测频率的增大两者的预测精度会逐渐朝同一程度逼近，且在整个W频段范围内，时序个数为50时预测误差变化保持基本平稳。

4.4不同预测模型间的预测精度比较

图7(b)为分别利用ITU-R模型、ARIMA(1,1,6)模型和Silva Mello模型对罗马地区某一时段雨衰预测的雨衰-频率变化曲线图，采用垂直极化方式，其中ARIMA(1,1,6)模型采用的预测间隔为0.10 GHz，时序个数为50，从图7(b)可看出，通过ARIMA(1,1,6)模型得到的W频段雨衰值与ITU-R, Silva Mello模型误差不超过1.5 dB。图8为分别使用这3种模型得到的均方根误差-频率曲线图，由图8可看出，在W频段，ARIMA(1,1,6)模型预测精度较高，且趋势较吻合，具有较好的预测效果。

4.5预测序列与仿真序列吻合度分析

图9为在76 GHz处使用ARIMA(1,1,6)模型，对2010年5月26日罗马地区某场雨仿真时序中的前1~440个序列预测第441~590时序得到的雨衰-序列图，其中，ARIMA(1,1,6)模型采用的预测间隔为0.10 GHz，时序个数为50。由图9可看出，在W频段，441~590预测序列和仿真序列间重合度较好，且变化趋势基本吻合，说明ARIMA(1,1,6)模型预测精度较高，有较好的预测效果。

图7 不同时间序列个数的预测误差及不同雨衰模型预测值比较

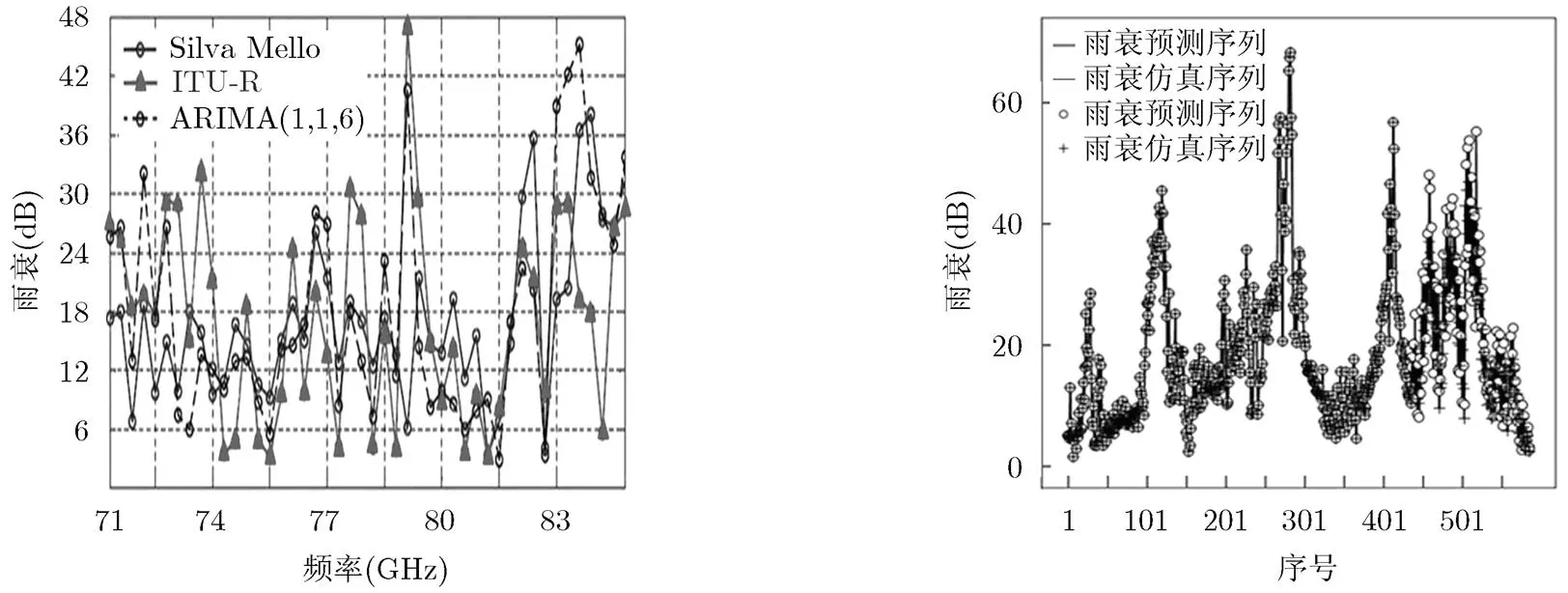
图8 均方根误差与频率的关系 图9 2010年5月26日雨衰预测与仿真时序对照

5 结论

本文针对降雨及其产生的雨衰多为不平稳事件，提出了基于非平稳时间序列ARIMA的W频段雨衰实时预测模型。该模型利用差分变换将非平稳时间序列转化为平稳时间序列，将该ARIMA(1,1,6)模型在不同极化方式、预测间隔、时序个数的条件下进行比较，结果表明，极化方式对模型参数的影响基本可忽略，而在满足预测间隔0.10 GHz，时序个数50，一阶差分的条件下预测误差不超过，然后与ITU-R, Silva Mello模型在垂直极化方式、预测间隔0.10 GHz，时序个数50的条件下进行比较，ARIMA模型属于线性模型，适合于短期预测，而ITU-R, Silva Mello模型为长期统计模型，该3种模型雨衰随频率变化趋势较吻合，而雨衰值相差不大，说明该ARIMA(1,1,6)模型与长期统计模型雨衰分布基本趋于一致。在使用该模型进行预测时，预测时序与仿真时序吻合度较高，验证了该方法可用于W频段雨衰预测，且预测精度较高，模型表述简单，因此，对W频段自适应抗衰减技术的研究和应用具有一定的参考价值。

[1] Cianca E, Rossi T, Yahalom A,. EHF for satellite communications: the new broadband frontier[J]., 2011, 99(11): 1858-1881.

[2] Nessel J A, Acosta R J, and Miranda F A. Preliminary experiments for the assessment of V/W-band links for space-earth communications[C]. IEEE Antennas and Propagation Society International Symposium(APSURSI), Orlando, FL, 2013: 1616-1617.

[3] Stallo C, Cianca E, Mukherjee S,.. UWB for multi-gigabit/s communications beyond 60 GHz[J]., 2013, 52(1): 161-181.

[4] Stallo C, Mukherjee S, Cianca E,.. System level comparison of broadband satellite communications in Ka/Q/W bands[C]. 2012 IEEE First AESS European Conference on Satellite Telecommunications (ESTEL), Rome, 2012: 1-10.

[5] Riva C, Capsoni C, Luini L,.. The challenge of using the W band in satellite communication[J]., 2014, 32(3): 187-200.

[6] Sacchi C and Rossi T. Overview of PHY-layer Design Challenges and Viable Solutions in W-band Broadband Satellite Communications[M]. Springer Berlin Heidelberg, 2010: 3-18.

[7] Pontes M S, da Silva Mello L, Willis M J,.. Eperimental data and testing procedures for modelling of propagation effects on terrestrial radio links from C to W bands[C]. 2012 6th European Conference on Antennas and Propagation (EUCAP), Prague, 2012: 86-90.

[8] Series P. Propagation data and prediction methods required for the design of Earth-space telecommunication systems[S]. Recommendation ITU-R, 2009.

[9] 赵振维, 卢昌胜, 林乐科. 基于雨胞分布的视距链路雨衰减预报模型[J]. 电波科学学报, 2009, 24(4): 627-631.

Zhao Zhen-wei, Lu Chang-sheng, and Lin Le-ke. Prediction model of rain attenuation based on the EXCELL rain cell model for the terrestrail line-of-sight systems[J]., 2009, 24(4): 627-631.

[10] Capsoni C and Luini L. The SC EXCELL model for the prediction of monthly rain attenuation statistics[C]. 2013 7th European Conference on Antennas and Propagation (EUCAP), Gothenburg, 2013: 1382-1385.

[11] 姜世泰, 高太长, 刘西川, 等. 基于微波链路的降雨场反演方法研究[J]. 物理学报, 2013, 62(15): 154303.

Jiang Shi-tai, Gao Tai-chang, Liu Xi-chuan,..Investigation of the invesion of rainfall field based on microwave links[J]., 2013, 62(15): 154303.

[12] 王辉, 魏文博, 金胜, 等. 基于同步大地电磁时间序列依赖关系的噪声处理[J]. 地球物理学报, 2014, 57(2): 531-545.

Wang H, Wei W B, Jin S,Removal of magnetotelluric noise based on synchronous time series relationship[J]., 2014, 57(2): 531-545.

[13] Nigam R, Nigam S, and Mittal S K. Stochastic modeling of rainfall and runoff phenomenon: a time series approach review[J]., 2014, 4(2): 81-109.

[14] Das D and Maitra A. Time series prediction of rain attenuation from rain rate measurement using synthetic storm technique for a tropical location[J].-, 2014, 68(1): 33-36.

[15] 杨明, 金晨辉, 张国双. 截断差分概率的上界估计与应用[J]. 电子与信息学报, 2014, 36(9): 2124-2130.

Yang M, Jin C H, and Zhang G S. Evaluation and application of the upper bound probability of the truncated differential[J].&, 2014, 36(9): 2124-2130.

[16] 弓树宏. 电磁波在对流层中传输与散射若干问题研究[D]. [博士论文], 西安电子科技大学, 2008: 25-61.

Gong S H. Study on some problems for radio wave propagation and scattering through troposphere[D]. [Ph.D. dissertation], Xidian University, 2008: 25-61.

[17] Ling S, Peng L, and Zhu F. Inference for a special bilinear time-series model[J]., 2015, 36(1): 61-66.

[18] 汪荣鑫. 随机过程[M]. 西安: 西安交通大学出版社, 2006: 132-143.

Wang R X. Random Processing[M]. Xi’an: Xi’an Jiaotong University Press, 2006: 132-143.

[19] Hansen P R and Lunde A. Estimating the persistence and the autocorrelation function of a time series that is measured with error[J]., 2014, 30(1): 60-93.

Rain Attenuation Prediction at W Band Based on Non-stationary Time-series ARIMA Model

Yang Feng Xue Bin Liu Jian

(,,’710077,)

Most existing rain attenuation prediction models are only tested at 55 GHz. There are small numbers of tested W-band rain attenuation prediction models, but these tested models have issues with high complexity and large quantities of calculations. A real-time prediction method is proposed that has a simpler structure and smaller quantity of calculations. The proposed method is based on the ARIMA model, which utilizes the relationship among the time series to establish a prediction model, conducts a stationary test on the original time series, transforms the nonstationary time series into a stationary time series by using a difference transform, and estimates the parameters of the stationary time series. This sequentially transforms the traditional nonlinear prediction into a linear prediction. First, the ARIMA (1,1,6) model is compared under the conditions of different polarizations, prediction intervals, and numbers of time series. Then the proposed model is compared with the International Telecommunication Union-R (ITU-R) and the Silva Mello rain attenuation prediction models using the conditions of vertical polarization, a prediction interval of 0.10 GHz, and a number of 50 time series. Finally, the forecasting time series with the simulant series are compared. The result shows that the prediction error between the ARIMA model, the ITU-R model and the Silva Mello model does not exceed, and that the change trend of the rain attenuation is basically the same. and the goodness of fit between the forecasting and simulant time series is good, which means that the proposed model can be applied to forecasting the rain attenuation in the W band, and that it has the advantages of simpler structure and high precision in prediction.

Rain attenuation prediction; W band; Non-stationary time-series; ARIMA; Difference

TN927

A

1009-5896(2015)10-2475-08

10.11999/JEIT150472

2015-04-27；改回日期：2015-07-20；

2015-07-27

薛斌 1085028568@qq.com

航空科学基金(20120196002)和雷达型空空导弹抗拖曳式诱饵方案研究

The National Aerospace Science Foundation of China (20120196002); The Research of Anti-TRAD in Air-to-Air Missiles with Radar Seeker

杨 峰： 男，1975年生，教授，研究方向为现代无线通信、卫星与移动通信等.

薛 斌： 男，1990年生，硕士，研究方向为卫星与移动通信.

刘 剑： 男，1978年生，副教授，研究方向为现代无线通信、阵列信号处理等.