基于分圆法的一类素数平方周期跳频序列族

徐善顶曹喜望许广魁



基于分圆法的一类素数平方周期跳频序列族

徐善顶*①②曹喜望②③许广魁②④

①(南京工程学院数理部 南京 211167)②(南京航空航天大学数学系 南京 211106)③(中国科学院信息工程研究所信息安全国家重点实验室 北京 100093)④(淮南师范学院数学与计算科学系 淮南 232038)

最大汉明相关与平均汉明相关是评价跳频序列族性能的两个重要参数。该文首先给出了源于Fermat商的广义分圆类的性质；其次，基于此广义分圆法构造了一类上的长度为，序列族的大小为的跳频序列族；最后证明了该跳频序列族关于最大汉明相关界与平均汉明相关界都是最优的。

跳频序列；Fermat商；分圆；最大汉明相关界；平均汉明相关界

1 引言

跳频技术被广泛应用于现代通信系统，比如超宽频、蓝牙、军事及雷达等。其中，用于控制载波频率跳变的地址码序列称为跳频序列(Frequency- Hopping Sequence, FHS)，它的性能对跳频系统有重大影响。在实际应用中，我们尽可能使用非平凡汉明自相关值和汉明互相关值较小的跳频序列以减少信号之间的彼此干扰，同时还要求序列的数目比较多以容纳尽可能多用户。但是，跳频序列族的参数受限于一些理论界，因此构造关于这些界的最优跳频序列族成了设计的热点。目前关于跳频序列族的汉明相关最优性的评价指标主要有如下两种：一种是最大汉明相关[1,2](MHC)，代表的是跳频系统的最坏情形，目前大多数跳频序列的设计主要是针对它的最优构造。另一种是平均汉明相关[3](AHC)，代表的是跳频系统的平均干扰状况，所以设计出达到平均汉明相关界的跳频序列族也意义重大。然而，公开发表的能同时达到最大汉明相关界与平均汉明相关界的跳频序列族[1,13,14]却比较少，这也成了序列设计中的一个重要课题。

分圆是一个很古老的数论问题，分圆数和广义分圆数被广泛应用于数论问题、组合数学、序列设计、编码理论以及密码学等。近年来，许多编码学者陆续利用Gauss经典分圆、Whiteman广义分圆、Ding-Helleseth广义分圆及其推广构造了一系列性能良好的序列。本文基于Fermat商[15]导出的广义分圆法[16]构造了一类长度为的跳频序列族，同时给出了各类汉明相关值的计算公式辅以验证其最优性。随后证明所构造的序列族不仅关于最大汉明相关界与平均汉明相关界都是最优的，而且序列族中的每个序列关于L-G界(见引理1)也是最优的。

2 基本概念

Lempel和Greenberger[1]于1974年给出了跳频序列的最大汉明自相关的一个下界：

引理1 (L-G 界[1]) 设是大小为的字符集上的长度为的任意跳频序列，则

引理2[2]设是大小为的字符集上的长度为的个跳频序列构成的序列族，则

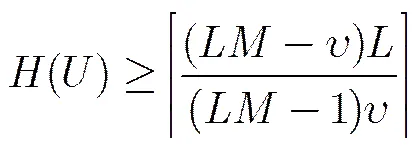
关于跳频序列族的另外两个重要参数：平均汉明自相关和平均汉明互相关，分别定义如下。

定义1[17]设是上的长度为的个跳频序列的集合且=，则分别称为

2008年，Peng等人[18]给出了跳频序列族的和的如下理论界：

引理3[18]设是上的长度为的个跳频序列的集合且=，则

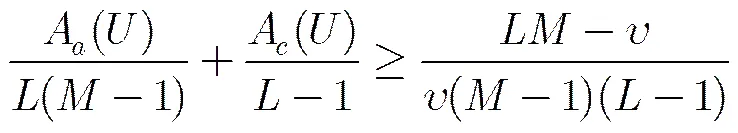
今后我们将使用以下定义:

注1：上面定义的关于环的阶广义分圆既不同于Whiteman广义分圆，又不同于Ding- Helleseth广义分圆中环的二阶广义分圆，是一种全新的分圆形式。

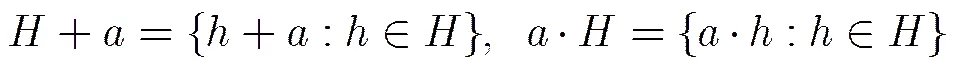
如上定义的广义分圆类与广义分圆数有以下性质：

性质1[16]若,，那么=,。

(3)易证。 证毕

综合(1)与(2)得结论。 证毕

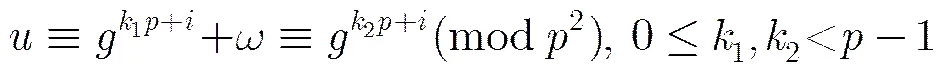
由性质4可得结论。

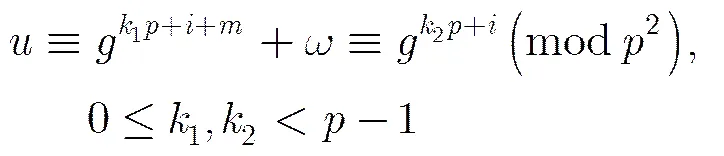
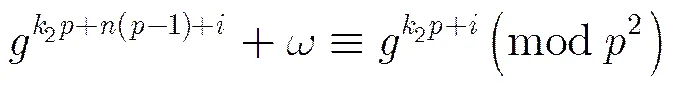
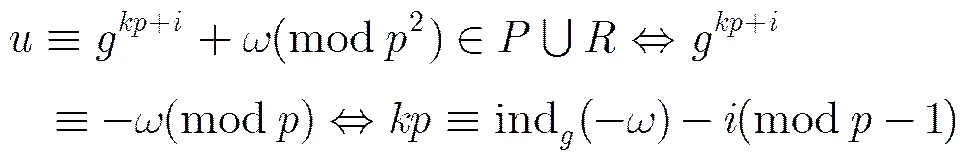
4 新的跳频序列族的构造

本节将构造一类新的跳频序列族，并利用上节的性质给出该跳频序列族的汉明相关值的分布，随后证明了所构造的序列族不仅具有最优MHC与最优AHC，而且序列族中的每个序列关于L-G界也是最优的。

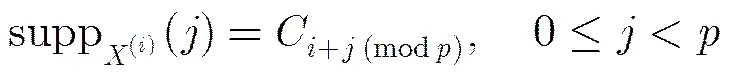
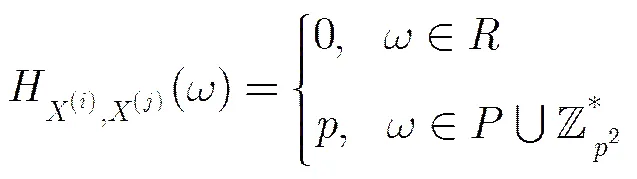
证明 (1) 显然成立；

由性质5，性质6，性质7可得结论。

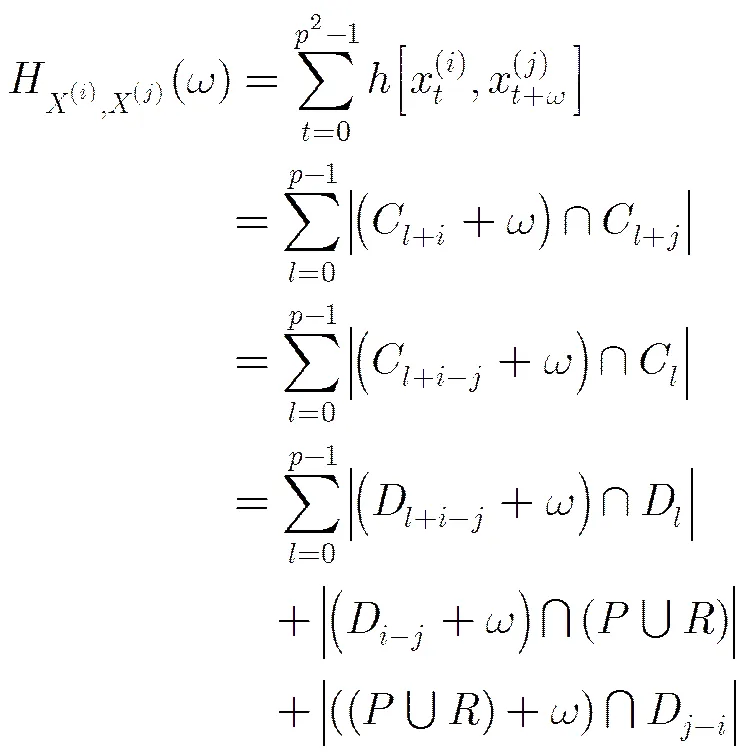
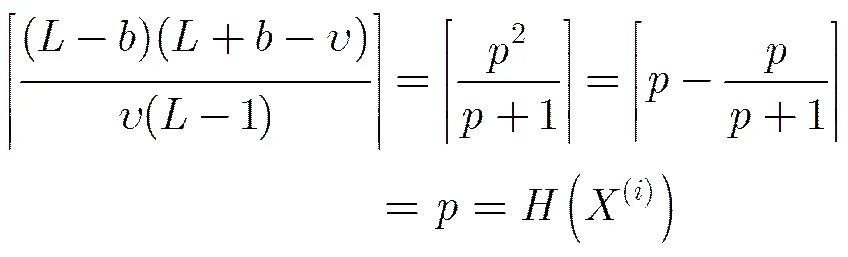
再由平均汉明自相关和平均汉明互相关的定义可得式(30)。把式(30)代入式(8)可得：

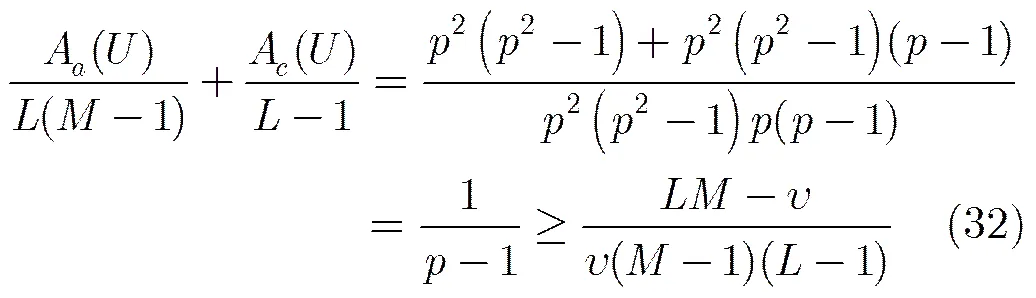
注2：本节与文献[13]构造的相似与不同之处：

(1)相似：与文献[13]所构造的跳频序列族相比，本节构造的序列族不仅具有与其相同的序列周期、序列个数和字符集大小，而且具有相同的最优汉明相关特性，即：所构造的序列族具有最优MHC和最优AHC，其中每个序列关于L-G界也是最优的(见表1)。

(2)不同：首先，本文与文献[13]所构造的跳频序列形式完全不同；其次，文献[13]中的构造主要利用广义bent函数，其序列族定义形式和最优性证明过程相对复杂。而本节中的构造主要采用的是广义分圆法，不仅定义字符集更加简洁，而且序列族构造方法简单可行，从而具有更强的应用背景。

表1几类相关跳频序列族的比较(其中为奇素数)

跳频序列族L|U|L-G界MHCAHC 文献[9]最优非最优最优 文献[13]最优最优最优 文献[14]最优最优最优 本文最优最优最优

5 结束语

[1] Lempel A and Greenberger H. Families of sequences with optimal Hamming correlation properties[J]., 1974, 20(1): 90-94.

[2] Peng D Y and Fan P Z. Lower bounds on the Hamming auto-and cross-correlations of frequency-hopping sequences[J]., 2004, 50(9): 2149-2154.

[3] Peng D Y, Niu X H, Tang X H,.. The average Hamming correlation for the cubic polynomial hopping sequences[C]. International Conference on Wireless Communications and Mobile Computing, Crete, Greece, 2008: 464-469.

[4] Ding C S and Yin J X. Sets of optimal frequency-hopping sequences[J]., 2008, 54(8): 3741-3745.

[5] Zhang Y, Ke P H, and Zhang S Y. Optimal frequency-hopping sequences based on cyclotomy[C]. First International Workshop on Education Technology and Computer Science, Wuhan, China, 2009: 1122-1126.

[6] Zhou Z C, Tang X H, Peng D Y,..New constructions for optimal sets of frequency-hopping sequences[J]., 2011, 57(6): 3831-3840.

[7] Zeng X Y, Cai H, Tang X H,.. Optimal frequency hopping sequences of odd length[J]., 2013, 59(5): 3237-3248.

[8] Ren W L, Fu F W, and Zhou Z C. New sets of frequency-hopping sequences with optimal Hamming correlation[J]., 2014, 72(2): 423-434.

[9] 刘方, 彭代渊. 一类具有最优平均汉明相关特性的跳频序列族[J]. 电子与信息学报, 2010, 32(5): 1257-1261.

Liu F and Peng D Y. A class of frequency-hopping sequence family with optimal average Hamming correlation property[J].&, 2010, 32(5): 1257-1261.

[10] Liu F, Peng D Y, and Zhou Z C. A new frequency-hopping sequence set based upon generalized cyclotomy[J]., 2013, 69(2): 247-259.

[11] 柯品惠, 章海辉, 张胜元. 新的具有最优平均汉明相关性的跳频序列族[J]. 通信学报, 2012, 33(9): 168-175.

Ke P H, Zhang H H, and Zhang S Y. New class of frequency-hopping sequence set with optimal average Hamming correlation property[J]., 2012, 33(9): 168-175.

[12] Zhang A X, Zhou Z C, and Feng K Q. A lower bound on the average Hamming correlation of frequency-hopping sequence sets[J]., 2015, 9(1): 55-62.

[13] Kumar P V. Frequency-hopping code sequence designs having large linear span[J]., 1988, 34(1): 146-151.

[14] Chung J H and Yang K. A new class of balanced near-perfect nonlinear mappings and its application to sequence design[J]., 2013, 59(2): 1090-1097.

[15] Agoh T, Dilcher K, and Skula L. Fermat quotients for composite moduli[J].1997, 66(1): 29-50.

[16] Chen Z X. Trace representation and linear complexity of binary sequences derived from Fermat quotients[J]., 2014, 57(11): 1-10.

[17] Peng D Y, Peng T, and Fan P Y. Generalised class of cubic frequency-hopping sequences with large family size[J]., 2005, 152(6): 897-902.

[18] Peng D Y, Peng T, Tang X H,..A class of optimal frequency hopping sequences based upon the theory of power residues[C]. Sequences and Their Applications (SETA 2008), Lexington, KY, USA, 2008: 188-196.

Class of Optimal Frequency-hopping Sequences Set with the Square of Prime Length Based on Cyclotomy

Xu Shan-ding①②Cao Xi-wang②③Xu Guang-kui②④

①(,,211167,)②(,,211106,)③(,,,100093,)④(,,232038,)

The Maximum Hamming Correlation (MHC) and the Average Hamming Correlation (AHC) are two important performance measures of the frequency-hopping sequences. Firstly, some properties of generalized cyclotomy are derived from Fermat quotient. Secondly, based on the generalized cyclotomy, a class of optimal frequency-hoppingsequences set with length of sequencesand size beingdefined onis constructed. Finally, it is proved that the proposed frequency-hopping sequences set is optimal with respect to the maximum Hamming correlation bound and the average Hamming correlation bound.

Frequency-hopping sequence; Fermat quotient;Cyclotomy; Maximum Hamming correlation bound; Average Hamming correlation bound

TN914.41

A

1009-5896(2015)10-2460-06

10.11999/JEIT150168

2015-01-29；改回日期：2015-05-29；

2015-07-06

徐善顶 sdxzx11@163.com

国家自然科学基金(11371011)和南京工程学院校级科研基金(QKJA201307)

The National Natural Science Foundation of China (11371011); The Foundation of Nanjing Institute of Technology (QKJA201307)

徐善顶： 男，1979年生，讲师，主要研究方向为跳频序列分析与设计.

曹喜望： 男，1965年生，教授，主要研究方向为代数组合论与代数密码学.

许广魁： 男，1981年生，讲师，主要研究方向为代数组合论与代数密码学.