基于灰色GM（1，1）模型的电能计量异常分析及判断

王　涓，吴旭鸣，尤　鋆，郁　浩，郑建勇

（1.泰州供电公司，江苏 泰州　225300；2.东南大学 电气工程学院，南京　210096）

基于灰色GM（1，1）模型的电能计量异常分析及判断

王涓1，吴旭鸣1，尤鋆2，郁浩2，郑建勇2

（1.泰州供电公司，江苏 泰州225300；2.东南大学 电气工程学院，南京210096）

1　背景

传统异常电能计量装置判断「1-2」的方法是周期性的对用户进行抽查，该方法滞后性较强，且存在较大盲目性。目前江苏省内每户已基本实现电子式电能表计量，其原理是对采样电压和电流信号进行处理并相乘转换成与电能成正比的脉冲输出显示，供用户自行查看，同时根据需要，将存贮的数据（电量等）上传给上位机（主站）。主站可以通过观察用户电压波形、相位等因素来判断计量表是否异常。但该方法存在以下几个缺点：①增加了供电单位的运营成本；②增加了布线的复杂性；③此装置可移植性能不高，对于已安装的装置进行2次使用时，要进行大量的人工拆卸和再安装，增加了电力公司的人力投入。

利用台区数据库中的数据建立合适的电力负荷预测模型，将预测值与测量值进行对比来判断电能计量装置是否异常。此类方法可以大大减少硬件开销和人员投入，效率高。电力负荷预测「3-7」是一个复杂的系统，其受到经济、政治、天气等多方面因素影响。对于如此复杂的系统只能获取其部分信息，无法获得其全部信息，这种系统符合灰色系统定义，因此可以对电力负荷预测系统建立灰色模型「8」。

2　灰色系统预测模型

2.1灰色系统理论

白色模型表示模型的信息全部已知，黑色模型表示模型的信息全部未知，灰色模型表示信息部分知道，负荷预测就是一个灰色问题，人们对于未来有关预测量信息部分已知「9」。灰色系统GM（1，1）模型自问世以来，在许多领域尤其是不确定性显著和缺乏数据的情况中，得到了广泛应用「10」。灰色模型建模的优越性体现在2个方面：其一是对原始数据要求不是很苛刻；其二是灰色模型一般采用一定的方式对原始数据进行生成处理（如：累加生成和累减生成），并将杂乱无章的原始数据整理成规律性较强的生成数据，从而弱化原始序列的随机性。

2.2查找异常电能计量装置模型建立

利用灰色系统理论建立用户负荷预测模型。

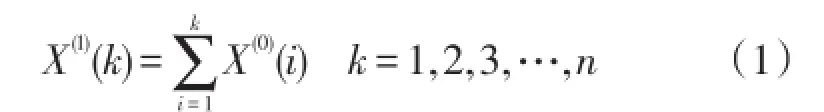
对累加后的序列采用一阶单变量微分方程进行拟合，得到白化方程GM（1，1）公式（2）

对模型中参数估计具体方式如下：设方程的参数数列为a^=（a，u）T，再设，将方程（2）按差分法离散可得公式（3）

欲确定系数，必须先求出B。令残差方程为公式（4）

由矩阵B和数据向量YN可最终求出a^，并确定方程的参数。

通过解微分方程得到该用户负荷预测累加模型为

其中k的预测值，则给出该用户初始值X（0）（1）后，利用方程则可以预估随后该用户的累加预测值。

利用累减公式还原得到用户负荷预测值为

其中X^（0）（k+1）为还原后的用户负荷预测值。

对于单一用户来说，电能计量装置异常表现为电能计量装置计量存在误差，所计量的用户用电量异常得大或者用电量异常得小，这些都是电能计量装置异常的表现。在判断用户电能计量装置是否存在误差时，根据用户的历史负荷值对当前负荷预测值进行调整，设置预判阂值上限和预判阂值下限。根据负荷预测值）计算预判阂值的上限和预判阂值的下限如下

式中：λmax和λmin分别为预判阂值上限因子和下限因子，根据用户的历史数据来调整选择合适的预判因子。

当用户的实际测量值大于预判阂值上限或小于预判阂值下限时，将该用户列为“排查对象”；反之，则该用户电能计量装置正常，将测得数据作为最新样本，并用来调整模型参数，准备进行下次预测。

3　灰色模型算法

基于灰色GM（1，1）模型的异常电能计量装置查找算法实现步骤如下：从用户用电系统数据库中获得用户电能计量装置正常计量的用电数据若干。将获得的数据样本按照时间顺序进行排列，对原始数据进行累加，形成新的有规律数据，对新的数据建立一阶线性微分方程模型，对模型进行辨识和参数估计得到预测方程，最后通过累减还原得到短期预测值。将获得的负荷预测值与用户电能计量装置采集的值进行比较，判断该用户的电能计量装置是否存在异常，若存在异常则将该用户列为“排查对象”；若不存在异常，则将测量得到的新的数据作为样本，以此样本对模型的参数进行重新估计，用以提高参数的准确性。

步骤一：获取用户计量装置取得的负荷历史数据若干。

步骤二：为了平滑数据，对原始数据进行一次累加。

步骤三：对模型参数进行估计，获得GM（1，1）模型。

步骤四：利用步骤三中模型获得用户负荷预测值。

步骤五：将负荷预测值与用户采集值进行比较判断用户电能表是否异常。

具体实现流程如图1所示。

4　实例结果与分析

4.1实例一

获得某台区2用户用电量若干，其中表1为用户5100021113用电量，表2为用户5100084628用电量。已知用户5100021113电能计量装置正常，用户5100084628电能计量装置存在异常。

图1　算法流程图

表1　用户5100021113用电量

续表

表2　用户5100084628用电量

续表

由表1得到用户5100021113电能计量装置计量正确的5天用电量，根据前5天实际用电量得到该用户第6天到第8天用电量预测值如图2所示，调整预判阂值的上下限因子，取预判阂值上限因子，预判阂值的下限因子，得到该用户的预判阂值的上下限，并与实际采集的用电量进行对比如图2所示。

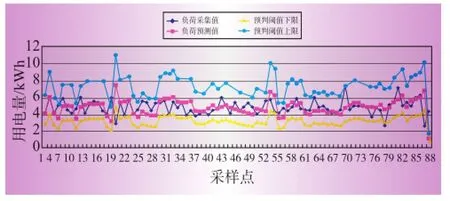
图2　用户5100021113实验结果

从图2中可以看出预测用电量与实际用电量较为接近，则该用户的电能计量装置计量不存在较大误差，将该用户最新采集到的测量值作为样本对模型参数进行调整以进行接下来的预测。利用该方法共预测了该用户接下来88天的用电量，该用户88天的实际用电量与用电量预测值较为接近，且在预判阂值的上下限之间波动，则判断该用户电能计量装置不存在明显误差。

4.2实例二

由表2得到用户5100084628电能表计量正确的5天用电量，根据前5天实际用电量得到该用户第6天到第8天用电量预测值如图3，调整预判阂值的上下限因子，取预判阂值上限因子，预判阂值的下限因子，得到该用户的预判阂值的上下限，并与实际采集的负荷值进行对比如图3所示。

图3　用户5100084628实验结果

从图3中可以看出预测负荷值与实际采集值较为接近，将该用户最新采集到的负荷值作为样本对模型参数进行调整，以进行随后的预测。该用户前50天的实际负荷值与预测值较为接近，从第51天开始到第64天该用户的负荷值异常低，低于预判阂值下限，则该用户电能计量装置存在较大误差可能性，将该用户列为排查对象，排查结果与分析结果吻合。这段时间的采集值不归入该用户的历史数据，利用牛顿插值法对这段时间的负荷值进行补充，以进行随后的预测。

5　结论

电能计量装置故障导致线损量异常，使供电企业蒙受巨大损失。因此，及时找出异常电能计量装置能有效减少供电公司损失。实验证明利用本文提到的基于灰色GM（1，1）模型的异常电能计量装置查找方法具有较好的工程实用性，缩短了排查周期，提高了供电公司排查效率，同时还减少了人力投入，为供电公司节约成本支出。

本文方法中涉及到的预判阂值上限因子和下限因子都是根据历史数据取平均值而得到的，因此这2个因子取值的精度不是很高，还需要对这2个因子的取值方法进行改进以提高整个算法的精度。D

「1」王杨.一种电能表异常运行现象的实验分析「J」.河北电力技术，2004，23（2）：46，51.

「2」王涓，吴旭鸣，王爱凤.应用皮尔逊相关系数算法查找异常电能表「J」.电力需求侧管理，2014，16（2）：52-54.

「3」刘思峰，党耀国，方志耕.灰色系统理论及其应用「M」.北京：科学出版社，2004.

「4」李伟，曹伟栋，袁亚南.基于组合函数和遗传算法最优化离散灰色模型的电力负荷预测「J」.电力自动化设备，2012，32（4）：76-79.

「5」李广，邹德忠，谈顺涛.基于混沌神经网络理论的小电网短期电力负荷预测「J」.电力自动化设备，2006，26（2）：50-52.

「6」张红旭，姚建刚，曹伟，等.基于改进灰色模型的超短期负荷预测「J」.电力系统及其自动化学报，2009，21（6）：74-77.

「7」Campbell P R J，AdamsonK.Methodologies for load forecasting「C」//Intelligent Systems，2006 3rd International IEEE Conference on.IEEE，2006：800-806.

「8」谢乃明，刘思峰.多变量离散灰色模型及其性质「J」.系统工程理论与实践，2008，28（6）：143-150.

「9」康重庆，夏清，刘梅.电力系统负荷预测「M」.北京：中国电力出版社，2007：36-37.

「10」邓聚龙.灰色系统理论基础「M」.武汉：华中科技大学出版社，2002.

Abnormal analysis and judgement of energy metering device based on GM（1，1）model

WANG Juan1，WU Xu-ming1，YOU Jun2，YU Hao2，ZHENG Jian-yong2
（1.Taizhou Electric Power Supply Company，Taizhou 225300，China；2.College of Electrical Engineering，Southeast University，Nanjing 210096，China）

利用灰色GM（1，1）模型建立用户负荷预测模型，并设定负荷预测阂值上限和阂值下限，将用户实际测量值与该用户负荷预测上下限阂值进行对比，若测量值不在上下限阂值之间，则将该电能计量装置列为“排查对象”；反之，电能计量装置正常，并将台区实际测量值作为样本对模型的参数进行重新估计，以提高参数的准确性。实例证明，灰色GM（1，1）模型在异常电能计量装置判断中具有较好的工程实用性。

异常电能计量装置；灰色GM（1，1）模型；负荷预测；上下限阂值

Energy metering device is one of the prerequisite for metering jobs in power companies.Its accuracy will directly affect the economic interests of the companies and users.Abnormal states that always appear to occurring to power metering devices，negative error tolerance particularly，will lead to higher of the line loss.This paper applies the GM（1，1）model to establish a user load forecasting model，then sets the load by forecasting the upper limits threshold and lower limits threshold.Comparing the measured load with the upper and lower limits threshold，if the measured value is not between the upper and lower threshold，then sets the user as‘subject for investigation'，otherwise，then sets it as a regular user.The measured value will be concluded as the samples of the model parameters for re-estimating in order to improve the accuracy of the model.Cases listed in this paper had proved that the GM（1，1）model has a decent practicability in finding unusual user.

abnormal electric energy metering device；GM（1，1）model；load forecasting；upper and lower limits threshold

TM933.4；TM715

B

2015-01-21；

2015-03-02

王涓（1981），女，江苏姜堰人，工程师，从事用电信息采集工作；吴旭鸣（1965），男，江苏泰州人，工程师，从事电力营销工作；尤望（1975），男，江苏南京人，副教授，博士，研究方向为新能源发电技术、电能质量监测与控制、电力电子在配网自动化中的应用；郁浩（1990），男，江苏南通人，硕士研究生，研究方向为电力电子设计及研发；郑建勇（1966），男，教授，博士生导师，研究方向为电力电子与电力传动。