蚁群算法在消防疏散平台上的应用

冯韦韦,裘 炅

(杭州电子科技大学 计算机学院,浙江 杭州 310018)

蚁群算法在消防疏散平台上的应用

冯韦韦,裘 炅

(杭州电子科技大学 计算机学院,浙江 杭州 310018)

为保证火灾现场人员能够快速安全疏散,在利用火灾探测系统得到火源位置信息的基础上,利用数据库技术对建筑节点、通道的静态和动态属性进行存储,并结合在建筑物空间结构模型的基础上,利用已改进的蚁群算法,找出人员疏散的最优路径,并将其通过智能指示灯动态显示方向,室外工作人员依据可视化界面显示的可行路径进行实时、快速调度,将该层平面图、疏散路径信息发送给事故现场人员。实验结果表明,该方法可使被困人员快速找到安全出口,有效减少人员和财产损失。

蚁群算法;人员疏散路径优化;动态显示;地图可视化显示

目前国内外的建筑多是高楼大厦且结构较为复杂,如何在多层建筑的多出口中找出最短路径成为人在紧急情况下最复杂的表现活动之一,受趋众性等因素影响表现为疏散速度缓慢、迷路等,大多数人采用具有正反馈性、分布式计算机制且富有建设性的贪婪启发式搜索[1]的蚁群算法获取最佳路径。人们提出了很多改进的疏散模型应用于安全疏散过程,且大多假设人群在疏散过程中总向最近出口行径,研究的重点在于降低蚁群算法运算时间,诱导蚁群寻找更优解。主流方法主要是在通道上以热辐射通量为限定条件获得障碍点[2],在比值函数的基础上设计了动态引导人移动路径的方法[3],将遗传算法的复制、交叉和变异等遗传算子引入蚁群算法或多蚁群算法[4],以提高收敛速度和全局搜索能力,另外引入一种确定性搜索方法,加快启发式搜索的收敛速度[5],但仍有缺陷。文中根据基于建筑物中各节点、通道的拓扑结构形成的蚁群算法对紧急疏散进行仿真。

1 模型建立

1.1 建筑物空间模型建立

建筑物可抽象为节点P和通道C组成,由G(P,C)表示,路径可表示为{G1,G2,…,Gi,…,Gm},m为路径总数。P为建筑物中所有节点的集合,可表示为{P1,P2,…,Pi,…,Pn},节点可分为普通节点、障碍节点,障碍节点为无法通过的节点,普通节点为除障碍节点以外的其他节点。节点Pi可表示为Pi(xi,yi,t,ni,fi)。其中xi、yi表示节点在t时刻的坐标,ni表示在该时刻时位于此节点的人员数量,fi表示节点类型。C是所有通道的集合,可表示为Cij{C12,…,Cij,…,Cmn},Cij表示节点i与节点j之间的可连接的通道。对应于蚁群算法中模型,疏散模型是以源点为蚁巢,以终点为食物。人群寻找出口的过程就是从源点经过一定的节点、通道到达终点的过程,不同的是人员疏散结束后无需返回源点。

1.2 人员选择策略

节点可分为0,BARRIER,START,END,MOVED五种类型,人员寻找出口的过程即是从START节点越过BARRIER节点选择0类型的节点并设置为MOVED,最终抵达END节点。初始化人员所在位置为START节点,从该节点周围的8个节点判断是否为0节点,若是则计算周围节点中各节点被选择的概率prob[i]和概率之和dbTotal,并利用轮盘算法进行选择。在轮盘停止转动则确定其为目标节点;若未停止则继续搜索节点,其中约束条件为:

if (prob[i]>=0) dbTemp=dbTemp-prob[i];

if (dbTemp<=0.0)

nIndex=i;

break;

当移动到一个可行节点时将其设置为MOVED类型并插入非禁忌表中,若该节点为END类型则计算本次行走的路径长度。

1.3 信息素更新策略

采用遗传算法中复制的思想继承优质个体的特性并进化,适应度高的个体被继承到下一代的概率大,反之概率则小。本文采用排序选择的方式,对所有个体进行排序来分配个体被选择的概率进而进行局部更新。选择的具体操作细节如下:(1)对所有个体按信息素浓度进行降序排列。(2)获得各个个体被选择的概率值。(3)将各个个体的概率值作为下一代的概率,利用轮盘算法来获得下一代。(4)初始时刻各疏散通道的信息素浓度相同,设ζij(0)=C,信息素更新函数ζij(t+n)=ρ×ζij(t)+Δζij(t,t+n)。ζij(t)为之前所有的信息素,ρ×ζij(t)为残留下的信息素,Δζij(t,t+n)为此时留下的信息素。信息素更新的步骤为:(1)获取所有个体的信息素浓度。(2)计算残留的信息素浓度。(3)获得所有个体中路径较短的某些优质个体的信息素浓度。(4)利用上式进行信息素更新。(4)完毕。

2 疏散路径寻优流程

人员在疏散过程中寻找最优路径的流程如图1所示。

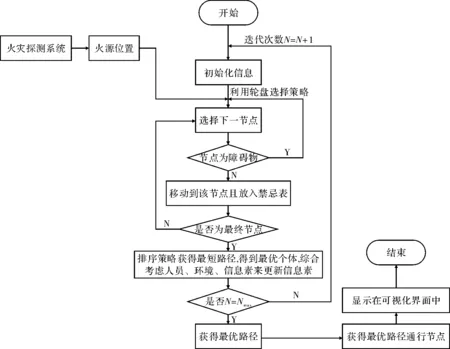
图1 流程图

蚁群算法主要包括4个步骤:参数初始化、选择下一个节点形成可行路径、更新信息素和获得最优解[6]。算法实现的过程可如下表示:

(1)初始化。

设置:t=0;N=0;ζij(t)=C;

tabuAry.Removeall();

ptCurrent=ptStart;

tabuAry.add(ptCurrent);

pMapAry[ptCurrent.x][ptCurrent.y]=1;

dbPathLength=0.0.

(2)判断下一个节点是否通行并记录当前位置、走过的路径集合和走过的位置,当此节点为终点时计算人员走过的路径长度,具体代码如下所示:

while(N<=Nmax)

for (int i=0;i

CPoint ptNext=ChooseNextCity();

tabuAry.Add(ptNext);

pMapAry[ptNext.x][ptNext.y]=MOVED;

ptCurrent=ptNext;

if (ptCurrent==ptEnd)

dbPathLength=CalPathLength();

其中,选择下一个节点的函数ChooseNextCity为:

for (int i=ptCurrent.x-1;i<=ptCurrent.x+1;i++)

for (int j=ptCurrent.y-1;j<=ptCurrent.y+1;j++) nIndex++;

if (从(x0,y0)到(x,y)路径允许)

prob[nIndex]=pow(pMapTrail[i][j],α)*pow(Q/pMapLen[i][j],β);

dbTotal=dbTotal+prob[nIndex];

nCount++;

为均衡随机性与正反馈机制,采用轮盘算法来实现“择优录取”原则上保持选择的随机性,从而弥补贪婪选择策略,避免陷入局部极值的问题[7]。

(3)从所有蚂蚁中获取前几名路径最短的蚂蚁,保存为最优个体。

(4)遗传复制思想来更新信息素。

dbTemp=1.0/最优个体走过的路径长度。

for (int j=0;j<最优个体路径点数;j++)

pt=bestAnt.tabuAry.GetAt(j);

pTrail[pt.x][pt.y]=pTrail[pt.x][pt.y]+dbTemp;

for (int i=0;i<周围环境宽度;i++)

for (int j=0;j<周围环境高度;j++)

pMapTrail[i][j]=pMapTrail[i][j]*ρ+pTrail[i][j];

保存最短路径和平均路径长度。

(5)若当前迭代次数为Nmax,则记录最优路径及路线,否则执行(1)。

(6)将获得最优集合节点显示在可视化界面中。

(7)结束。

3 算法可行性分析

3.1 节点可行性策略

本文算法将建筑物节点分为起始、终止、障碍物、未过和已过5种类型,节点为未过且非障碍物类型作为选择下个节点的策略之一,用禁忌表保存走过节点以防止形成环路;在当前节点的周围节点可通行的情况下,确定由信息素和节点间距离决定节点被选择的概率,用轮盘算法的思想将该概率与概率和的随机数进行比较,若随机数小即轮盘停止转动,则记录该概率从而确定对应节点为下一选择节点,图2为起始点到终点间路径图。

图2 路径图

3.2 收敛性分析

图3所示为本文算法中疏散路径长度与迭代次数的关系,上方表示平均路径曲线,下方表示最短路径曲线。从图中可以看出,在40代以前的各代路径长度不一,波动较大,在40代左右时各代疏散平均路径和最短路径几乎重合,路径长度为30～35之间时疏散趋于稳定。

图3 收敛图

3.3 局部收敛与全局搜索均衡性

传统算法直接采用全局信息素进行更新,忽视了最优个体的信息素浓度,本文通过遗传算法保存最优个体并及时反馈到信息素的更新,在信息素更新时利用遗留的信息素与最优个体的信息素之和来进行更新,从而加快了收敛速度。为均衡搜索范围,使用轮盘算法将周围选择节点随机化而不仅局限于信息素浓度大小形成的正反馈机制,减小信息素对概率的影响而扩大了全局搜索能力,实现了保留较优个体的影响且亦能够进行随机化全局搜索。

4 火灾疏散仿真

本文蚁群算法相较最大-最小算法具有较强的优越性,对这两种算法的收敛速度进行对比,结果如表1所示。从表1中可以看出,本文算法比最大-最小算法能够更快找到最优解。

表1 与最大-最小算法的收敛速度比较

某建筑发生火灾,该建筑内的人员都需疏散到安全出口处,通过同一个房间和不同房间这两种疏散模型来体现仿真的效果。图4所示为一个容纳15人的有两个出口且有障碍物的房间,随着时间的推移,人员陆续走向两个出口,人员选择出口的原则是走向较近出口,当此条路径上的人员遇到障碍物时能自行避开障碍物并继续前行,在行进过程中若该路径上人员过多,即这条通道中信息素浓度过大,于是搜索全局解,走向另一个出口。

图4 房间中疏散模拟

根据人员流动的特点,对出口利用率形成如图5所示的曲线,其中实线表示上面出口A的流量图,虚线表示出口B流量图,当A中流量过多时,B总可以对其保持平衡。

图5 出口利用图

图6所示为在多楼层情况下人员的疏散过程,通过其中的路径线条可以看出,人员都是集中向出口走去,此时与一个房间不同,这里的目的出口只有一个而且在最底层,在楼梯口处会造成拥挤,易发生事故。

图6 多楼层疏散模拟

5 结束语

本文以蚁群算法为基础求解出人员疏散的最优路径,根据现场势情的变化综合考虑火灾、通道、人员等的通行能力而进行动态求解最优路径进行疏散。针对蚁群算法易收敛局部最优的缺陷,提出了结合轮盘选择和遗传复制算法的思想进行节点选择决策。目前仍有问题需要解决,可对风险参数进一步修订以提高实现的准确性;需利用多态蚁群思想对人员功能进行分工得出不同类型的信息素轨迹;另外可引用更佳的算法在加速收敛和全局最优的基础上进行优化,应可预测事故发展趋势、判断事故等级,为部署指挥救援工作提供决策依据[9]。另外可在某段区域都有固定的社区群组,例如学校、小区等通常会有论坛,使所在人群都订阅该论坛的消息,紧急情况发生时,以类似新闻的功能推送紧急信息,便于事故现场人员对所处环境进行了解。

[1] Marco Dorigo,Vittorio Maniezzo,Alberto Colorni.Ant system optimization by a colony of cooperating agents[J].IEEE Transactions on Systems,Man,and Cybernetics,1996,26(1):28-41.

[2] 贾磊,程乃伟.基于蚁群算法的动态疏散路径改进[J].科技传播,2013(20):85-86.

[3] 邢志祥,丁芙蓉.城市人员密集场所应急救援决策支持系统研究进展[J].工业安全与环保,2014,40(2):59-62.

[4] 李永林,叶春明,刘长平.轮盘赌选择自适应和声搜索算法[J].计算机应用研究,2014(6):1665-1668.

[5] 崔喜红,李强,陈晋.大型公共场所动态引导人移动路径设计方法[J].中国安全科学学报,2008(11):48-54,177.

[6] 梅志斌,董文辉,潘刚,等.建筑物火灾中人员疏散路径优化自适应蚁群算法[J].沈阳建筑大学学报:自然科学版,2008(4):671-674.

[7] 段鹏飞,熊盛武,李辉.面向大型场馆疏散的改进多蚁群算法[J].计算机应用研究,2013(2):357-359,363.

[8] 陈娟,马晓慧.基于TSP的蚁群算法研究[J].现代计算机:专业版,2013(3):8-11.

[9] 项前,赵永光.基于多目标蚁群优化的交通路径优化研究[J].微计算机信息,2012(5):8-9,47.

Application of Ant Colony Algorithm in Fire Evacuation Platform

FENG Weiwei,QIU Jiong

(College of Computer Science,Hangzhou Dianzi University,Hangzhou 310018,China)

In order to ensure the quick and safe evacuation from the fire,database is used to store information of traffic nodes and the static and dynamic states of the channel of buildings with the help of fire information from the fire detection system.On the basis of the building spatial structure model,the optimal path of evacuation is found by the improved ant colony algorithm,and then the direction is dynamically shown through intelligent indicators.Other related personnel can make a real time and quick scheduling according to the visual interface and then send maps and paths to people who are in fire.Experiments show that this method can make people find the exit more quickly,so it can reduce the loss of personnel and property in fire.

ant colony algorithm;evacuation route optimization;dynamic display;map visualization

2014- 09- 21

冯韦韦(1989—),女,硕士研究生。研究方向:消防物联。E-mail:475707372@qq.com

10.16180/j.cnki.issn1007-7820.2015.04.004

TP301.6

A

1007-7820(2015)04-013-04