不同媒介中的参量阵近场声场研究

李中政，方尔正

不同媒介中的参量阵近场声场研究

李中政1,2,3，方尔正1,2

(1. 哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001； 2. 哈尔滨工程大学水声工程学院，黑龙江哈尔滨 150001；3. 海军92198部队，辽宁兴城125100)

在众多描述非线性声波传播的理论模型中，KZK方程能够准确地描述有限振幅声波传播的衍射、吸收及非线性效应，对求解参量阵近场声场有着明显的优势，因而成为描述非线性声场最为精确的方程之一。从KZK方程的频域求解出发，利用二阶对角隐式龙哥库塔法(second-order Diagonal Implicit Runge-Kutta, DIRK2)和Crank-Nicolson有限差分法(Crank-Nicolson Finite Difference, CNFD)相结合的有限差分算法，对在不同媒介中传播的参量阵近场声场特性进行研究，旨在对参量阵能量累积过程有进一步的理解，为参量阵转换效率的提高提供初步的探索，为参量阵的进一步工程应用提供相应的理论指导。

参量阵；近场声场；KZK方程；传播媒介

0 引言

参量阵具有低频、宽带、高指向性及低旁瓣的优点，广泛应用于鱼群探测、掩埋水雷探测、海底环境监测、水下通信等水声工程领域[1-3]。与此同时，参量阵的转换效率很低，严重限制了参量阵的进一步工程应用。观察描述参量阵的Westervelt理论模型可知，参量阵的功率转换效率与传播媒介的密度、声波传播速度、非线性参量以及声吸收系数息息相关[2]。恰当选择参量阵传播媒介，可以有效提高转换效率。

自上个世纪60年代Westervelt[4]首次提出了参量阵的理论模型，国内外开展了广泛的理论和应用研究。目前，在众多描述参量阵声场传播的理论模型中，Westervelt方程[4]和Berktay远场解[5]在求解参量阵近场时，做了很多近似，建立的物理模型不够精确。并且采用体积阵模型对虚源求体积积分时，源点同时又是场点，被积函数中会产生奇点[6]。KZK方程[7,8]充分考虑了非线性、吸收和散射效应，避免了对虚源求体积积分，可以更精确地建立声学参量阵模型，基于其解析解的复杂性，很多学者[9-11]采用数值有限差分进行求解。

本文利用KZK方程的频域求解方法，对在不同媒介中传播的参量阵近场声场特性进行研究，其目的在于寻求提高转换效率的新途径，为参量阵进一步的工程应用提供理论指导。

1 理论基础

描述参量阵近场声场传播过程中吸收、衍射和非线性效应的KZK方程如式(1)所示：

(4)

本文采用DIRK2法和CNFD法相结合的有限差分方法对KZK方程进行频域求解，相比之前诸多文献中后向隐式有限差分法(IBFD)和CNFD法相结合的有限差分方法，该求解方法有两方面的优势：

(1) 在接近换能器表面的区域，声压幅值振荡激烈，采用IBFD法和非常小积分步长可以得到较为稳定的解，但是DIRK2可利用更大的步长来达到KZK方程求解需要的稳定性；

(2) DIRK2法具有二阶计算精度，其求解结果能更好地跟CNFD相匹配。

本文的仿真对象是圆形活塞声源，根据参量阵的形成条件，其初始条件即层上任意阶谐波系数、可以表示为

2 仿真条件及其结果分析

本文采用的换能器阵元为圆形活塞声源。计算坐标如图1所示。

为减少计算时间和计算结果的数据量，基于圆形活塞声源辐射声场的轴对称特性，化三维计算区域为二维平面，采用和边界拟合程度最佳的矩形网格对计算区域分割。

2.1 媒介参数选取

理论表明，具有不同物理属性的声波传播媒介中存在不同的非线性作用机理。水、甲醇、乙醇都是比较常见的液体，其中甲醇、乙醇中声速较低，是较为典型的慢波导介质，对参量阵近场声场的分布有着非常重要的影响。FC-43是一种无色透明的全氟化学品，具有良好的化学惰性、电气绝缘性能及热传导性，广泛应用于仪器仪表的抗腐蚀隔离、电子器件检漏等领域。作为一种低声速、高密度的稳定介质，本文将其作为参量阵传播的一种特殊媒介对其进行研究，为了研究的方便，本文认定其吸收系数等同于硅油。

查阅相关文献，得到反映不同媒介的物理性能参数如表1所示。

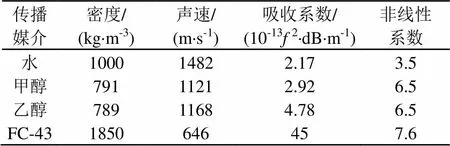
表1 不同媒介的物理性能参数

2.2 原波轴向、径向声场的变化规律

参量阵声场的空间分布特性研究是参量阵工程应用的理论基础，先对两列原波的声压幅值随轴向、径向距离的变化规律进行研究。

综合分析图2~5，得到如下结论：

(1) 由图2、4可知，原波声压幅值在不同传播媒介中的变化规律大抵相同，在法线方向由于菲涅尔衍射现象，近场声压幅值振荡激烈，声压幅值极大值和极小值交替分布；远场则呈现单调的球面波吸收。

(2) 从图3、5可以看出，高频原波辐射声场具有高指向性特性，在轴向距离处的旁瓣明显低于主瓣。

(3) 原波近场声压幅值的变化取决于边缘声线和轴向声线的声程差，当其为半波长时，会形成声轴方向声压幅值的最后一个极大值，本文仿真结果显示极大值出现位置顺序为FC-43、水、乙醇、甲醇，由波长和声速的关系式可知，不同媒介中的声速是声压幅值最后一个极大值出现位置的决定性因素。

2.3 参量阵差频波的轴向、径向及其空间分布仿真

本节对不同媒介中的参量阵声场进行分析。

图6~11分别给出参量阵差频波的近场声场空间分布特性，观察发现：

(1)不同媒介中的参量阵差频波均为高指向性的波束，说明高频原波的非线性作用可以在不同的媒介中进行。

(2) 仿真结果表明：当吸收系数相差不大时(甲醇、水)，声速越小、密度越低，参量阵差频波声压幅值越大，能量累积的轴向距离越长；当密度、声速相差不大时(甲醇、乙醇)，吸收系数的大小直接决定了参量阵差频波幅值；尽管FC-43和水的物理属性相差较大，吸收系数非常大，但是其较小的声速仍然给参量阵的声场转换效率带来了相当的研究价值。

(3) 由图6可知，不同媒介中参量阵差频波能量累积过程大致相同，参量阵差频波的能量累积过程存在一个拐点，在原波相互作用较强的近场区域，差频波的吸收速度小于由于非线性作用参量阵的形成速度，随着轴向距离的增加，非线性作用减弱，超过拐点之后，能量累积过程由于原波吸收变得缓慢。此时，差频波的吸收是制约参量阵作用距离的主要因素。因此，如何扩大参量阵的能量累积作用区是提高参量阵转换效率的关键所在。

3 结论

本文通过利用DIRK2和CNFD相结合的频域有限差分法求解描述参量阵近场声场特性的KZK方程，对不同媒介中的参量阵近场非线性声场特性进行了研究。结果表明：不同媒介中的参量阵声场传播特性与媒介的密度、声速、吸收系数等息息相关，对高频共轴原波的非线性作用机制均会产生直接的影响。增大非线性参数，降低媒介密度、声速均可以有效改善参量阵差频波的能量累积过程。从参量阵工程应用的角度讲，本文可为参量阵转换效率的提高提供相应的理论基础。

[1] 钱祖文. 非线性声学[M]. 北京: 科学出版社, 2009, 166-179.

QIAN Zuwen. Nonlinear Acoustics[M]. Beijing: Science Press, 2009, 166-179.

[2] 何祚镛, 赵玉芬. 声学理论基础[M]. 北京: 国防工业出版社, 1986, 416.

HE Zuoyong, ZHAO Yufang. Theoretical foundation of acoustics[M]. Beijing: National Defense Industry Publishing House, 1986, 416.

[3] 李颂文. 参量阵及其在水声工程中的应用进展[J]. 声学技术, 2011, 30(1): 9-16.

LI Songwen. Parametric array and its application in underwater acoustic engineering: an overview[J]. Technical Acoustics, 2011, 30(1): 9-16.

[4] Westervelt. P. J. Parametric acoustic array[J]. J. Acoust. Soc. Am, 1963, 35(4): 535-537.

[5] Berktay. H. O. Possible Exploitation of Nonlinear Acoustics in Underwater Transmitting Applications[J]. J. Sound and Vibration, 1965, 2(4): 435-461.

[6] 李颂文. 不同波束形成的参量阵近场比较[J]. 声学技术, 2001, 20(2): 81-83.

LI Songwen. Comparison of nearfields of several kinds of parametric array[J]. Technical Acoustics, 2001, 20(2): 81-83.

[7] Zabolotskaya E A, Khokhlov R V. Quasi-plane waves in the nonlinear acoustics of confined beams[J]. Sov. Phys. Acoust, 1969, 15(1): 35-40.

[8] Kuznetsov V P. Equations of nonlinear acoustics[J]. Sov. Phys. Acoust, 1970, 16(4): 467-470.

[9] Aanonsen S I, Barkve T, Tjøtta J N. Distortion and Hannonic Generation in the Near-field of a Finite Amplitude Sound Beam[J]. J. Acoust. Soc. Am., 1984, 75(3): 749-768.

[10] Thomas L. Szabo. Time domain wave equations for lossy media obeying a frequency power law[J]. J. Acoust. Soc. Am., 1994, 96(1): 491-500.

[11] Naze Tjøtta J, Tjøtta S, Vefring E H. Propagation and interaction of two collinear finite amplitude sound beams[J]. J. Acoust. Soc. Am., 1990, 88(6): 2859-2870.

[12] Naze Tjøtta J, Tjøtta S, Vefring E H. Effects of focusing on the nonlinear interaction between two collinear finite amplitude sound beams[J]. J. Acoust. Soc. Am., 1991, 89(3): 1017-1020.

Research on the parametric array’s near-field acoustic characteristics in different mediums

LI Zhong-zheng1,2,3, FANG Er-zheng1,2

(1. Acoustic Science and Technology Laboratory, Engineering University, Harbin 150001,Heilongjiang, China;2. College of Underwater Acoustics Engineering, Harbin Engineering University, Harbin 150001,Heilongjiang, China;3. Unit 92198 of Naval, Xingcheng125100, Liaoning, China)

In numerous theoretical models of describing the nonlinear acoustic wave propagation, the KZK equation can accurately describe diffraction, absorption and the nonlinear propagation effects of finite amplitude sound beam, thus becomes one of the most accurate equation describing nonlinear ultrasonic field. In this paper, based on the frequency domain solution of the KZK equation, using second-order Diagonal Implicit Runge-Kutta(DIRK2) method and the Crank-Nicolson Finite Difference(CNFD) method of finite difference algorithm, the near-field acoustic characteristics of the parametric array in differentpropagation mediums are studied, the results of this paper may provide the corresponding theoretical basis for further engineering application.

the parametric array; acoustic characteristics of the near-field; KZK equation; propagation medium.

TB551

A

1000-3630(2015)-03-0193-05

10.3969/j.issn1000-3630.2015.03.001

2014-04-24;

2014-07-20

基于某平台的参量阵技术研究(9140c20010613c20078); 国家自然科学基金青年科学基金资助项目(11204050)

李中政(1984－), 男, 山西平遥人, 博士研究生, 研究方向为非线性声学。

方尔正, E-mail: fangerzheng@hrbeu.edu.cn