云平台下并行总体经验模态分解局部放电信号去噪方法

宋亚奇 周国亮 朱永利 李 莉 王德文



云平台下并行总体经验模态分解局部放电信号去噪方法

宋亚奇1,2周国亮1,2朱永利1,2李 莉1,2王德文1

（1. 华北电力大学控制与计算机工程学院 保定 071003 2. 华北电力大学新能源电力系统国家重点实验室 北京 102206）

信号去噪是对输变电设备进行在线监测和诊断时首要解决的问题。鉴于总体经验模态分解（EEMD）方法对局部放电信号进行去噪的优势，设计了基于MapReduce模型的并行化EEMD算法（MR-EEMD），利用云平台提高算法的计算效率。在对分段包络线进行重构时，针对矩形窗的固有缺陷，提出了基于局部平稳度的自适应分段包络线重构算法（LF-ASER）进行分段边界的补偿处理，使重构的包络线误差减小到给定阈值范围内。实验结果表明MR-EEMD算法相对于EEMD性能提升显著，适合处理变压器的局部放电等高采样率信号，同时保持了EEMD去噪效果，并获得较高的可扩展性和加速比。

局部放电 信号去噪 总体经验模态分解 MapReduce 包络线重构

0 引言

局部放电的检测对于大型电力变压器在线监测和故障诊断具有重要的实际意义。局部放电信号通常非常微弱，而数据采集现场往往又存在大量的噪声干扰[1]，可能将局部放电信号淹没。因此，如何正确地从采集到的信号中提取出局部放电信息是变压器进行在线监测时首要解决的问题。

目前，普遍采用小波变换方法进行信号去 噪[2,3]，但是小波去噪方法受小波基函数选择、分解层数确定和阈值选择等因素影响，缺乏自适应性。经验模态分解（Empirical Mode Decompositio，EMD）[4]可以自适应地处理非线性、非平稳的复杂信号，而且能解决一些小波变换不能解决的问题，一些学者研究利用EMD进行局放信号去噪[5,6]。与常规的小波去噪算法相比，EMD方法对时频平面的铺砌方式没有任何限制，分解所得的每个IMF都反映了信号中的一种特有频率信息，不受小波母函数和最佳小波分解层数选取的限制，去噪效率和准确性更高[7]。但由于EMD方法存在固有缺陷，使得信号分解过程中会产生模态混叠现象，一些学者研究使用EMD的改进算法EEMD进行信号去噪[8,9]，并取得较好的效果，但相关文献没有考虑现有信号分析仪器采样率高（数据量大）且总体经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）分解运算量大的问题。不论EMD和EEMD，在进行信号分解过程中，都需要利用三次样条插值算法进行上下包络线的拟合，过程中需要进行多次迭代，算法计算量大、运行速度缓慢[10]。在快速算法研究方面，文献[11]放弃三次样条插值，采用简化的拟合方法，并适当放宽终止准则。文献[12]采用B样条插值函数构造包络线。文献[13]只对有效数据进行拟合和进行终止准则判定。文献[14]建立滤波器组提取各个分量，以提高算法计算速度。但是这些方法在进行分段处理时，划分处引发端点效应问题，进行重叠划分时，由于各段取均值的次数不同，引起划分处的不连续问题。随着近年来大规模云计算平台的出现，能否利用云计算平台设计并行化的EEMD，加速算法执行，并消除上述快速算法的问题。在众多云计算技术中，Hadoop[15]云计算技术专长在于大数据存储和处理，提供了MapReduce并行编程模型[16]，能够自动并行执行大规模计算任务，隐藏底层实现细节，降低并行编程的难度，近年来在各类数据密集型系统中得到广泛应用[17]。这为实现快速的EEMD去噪提供了全新的思路。

本文应用MapReduce模型设计实现并行化的EEMD算法MR-EEMD，以提高高采样率信号的处理速度。在对数据边界处理时，设计了基于局部平稳度的自适应分段包络线重构算法LF-ASER进行补偿处理，确保分段包络线在边界处连续，实现包络线的准确重构，以保持原始EEMD算法去噪效果，同时获得Hadoop平台提供的高可靠性和高性能。

1 EEMD去噪

1.1 总体经验模态分解EEMD

总体经验模态分解（EEMD）方法[18,19]是由Flandrin的EMD算法研究小组和Huang的研究小组共同提出EMD改进方法，用以改善EMD在降噪的过程中存在模态混叠现象。EEMD是通过加入白噪声而进行辅助分析的算法，其本质是人为添加强度相同但序列不同的白噪声来补充信号中缺失的尺度，并对得到的信号进行分解。文献[18]指出，当添加噪声重复次数达到100次，并且强度为0.1～0.3时，能够取得较好的结果。

对信号进行EEMD分解之后得到的每层IMF分量的中心频率均严格保持为前一层IMF中心频率的一半[20,21]，因此可以通过选取适当频率范围的IMF以获得不同的滤波效果。

1.2 阈值处理

对白噪声进行EEMD分解所产生的各个分量中，最先分解出来的几层IMF分量通常仅由噪声产生，可直接滤除。随后分解的IMF分量既包含噪声分量又包含有用信号分量，需要进行阈值处理。分解最后得到的IMF分量是仅由有用信号产生的，可直接保留，重构后的信号表示为

1.3 去噪评价系数

为评价去噪效果，采用信噪比SNR和波形相关系数NCC来描述去噪后的信号和原信号的相似程度[22]，即

2 基于MapReduce模型的并行化EEMD算法

2.1 MapReduce并行计算模型

MapReduce是一种编程范式，主要用于数据密集型应用，可以有效处理集群中节点故障，并扩展到几千节点。模型中数据表示为（key，value）的形式。一个MapReduce任务包含三个阶段：Map、Shuffle和Reduce，如图1所示。在Map阶段，map函数接收输入对（1，1），并产生一个或多个输出对（2，2）；在Shuffle阶段，输出对被划分并传递给reduce函数；在Reduce阶段，拥有相同key的（key，value）对被放在同一组中（2，list(2)），交由reduce函数处理并输出最终结果（3，3）。

图1 MapReduce的数据流图

2.2 EEMD算法性能分析

EEMD通过循环迭代计算个IMF分量。在单次迭代过程中，计算量最大的过程是求曲线极值点，并根据极值点，利用三次样条插值求解曲线的上、下包络线。通过在程序中加入计时器，多次统计表明，求上、下包络的时间占求解IMF时间的85%左右（通过变换处理信号长度计算各过程占用时间，多次求平均时间占比所得）。因此，提高算法整体性能的关键就是加快曲线上、下包络线的求解过程。

有研究学者利用多核，基于MPI设计实现了并行化的三次样条插值算法[23]。与传统的并行计算不同，MapReduce强调数据并行，即将数据拆分成多个部分，利用多个计算节点并行处理分布式的数据，然后进行汇总。因此首先需要对原始信号进行分段。

2.3 基于矩形窗的自适应数据分段及边界补偿处理

本文采用矩形窗函数对原信号截断，形成多个信号分段。矩形窗属于时间变量的零次幂窗，其函数形式为

并行处理任务在各自的矩形窗内求解信号分段的包络线，之后对分段包络线进行连接重构。一种简单的重构方法

为每个窗的采样点数。但是这种简单的重构方式未考虑矩形窗的固有缺陷，重构得到信号整体包络线与原始信号包络线相比，形状发生了扭曲，如图2所示。

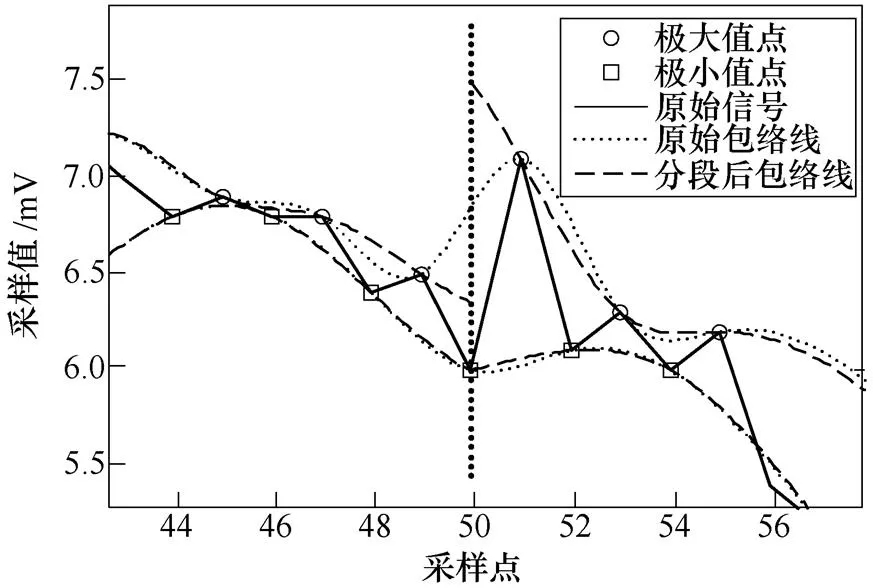
（a）选取某极小值点作为分界点

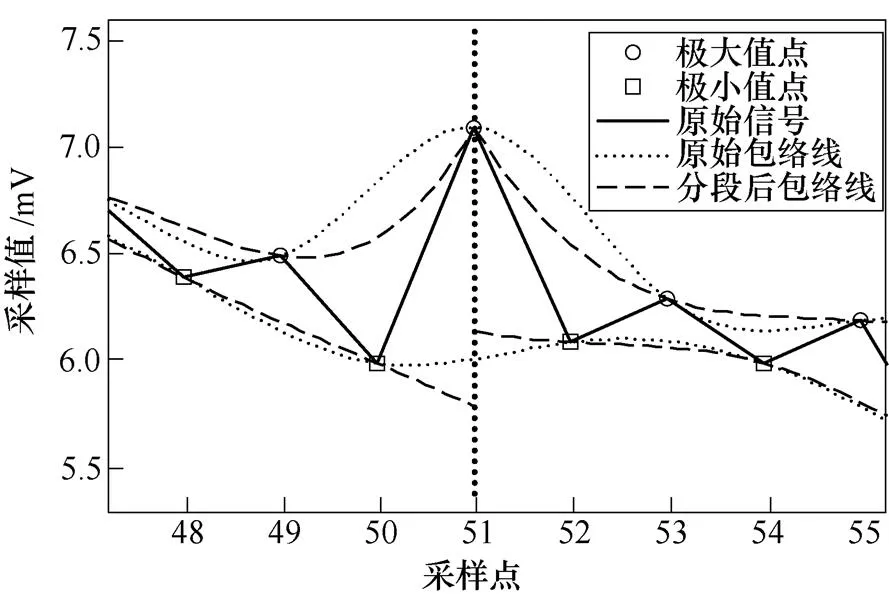
（b）选取某极大值点作为分界点

图2为随机选取的一段变压器局部放电信号，选取不同的分界点，分别画原始信号包络线和分段信号的包络线。图2a选取某极小值点（=50）作为边界，下包络误差相对较小，上包络误差较大。图2b选取某极大值点（=51）作为边界，上、下包络线均存在较大误差。因此，若采用式（7）对分段包络线进行连接重构，需要额外的处理机制对分界点附近曲线进行修正。

为了减小分段包络线误差，一种可行的方法是对窗口进行延拓。当选取的窗口边界不同时，为获得相同的包络线误差，需要延拓的长度不同，本文首先给出延拓代价的概念。

定义1 延拓代价是使分段包络线与总体包络线的误差小于指定阈值需要对矩形窗口进行延拓的长度。

延拓长度直接影响到包络线重构时计算量的大小，延拓长度越小越好。因此，应尽量选择信号平稳、变化较小的点作为窗口边界，使包络线重构时的延拓代价尽可能小。

从图2中可以看出，无论窗口边界选择的是极大值或极小值点，上、下包络线均可能存在较大误差，误差大小主要取决于边界点前后信号值的差异大小。边界点前后信号值越平稳，变化越小，则分段包络线的误差越小，反之，则越大。为获得平稳的窗口边界，本文给出信号局部平稳度的概念，定量地描述信号局部变化剧烈程度，用以自适应地确定窗口边界。

针对上述矩形窗分段时存在的问题，基于信号局部平稳度和延拓代价的概念，提出基于局部平稳度的自适应分段包络线重构（Local Flatness-Adaptive Segmentation Envelope Reconstruction，LF-ASER）算法。算法的主要思想是：为保证尽量减小重构误差，首先根据原始信号波形局部平稳度对用于分段的矩形窗边界进行自适应选取，即通过逐点计算局部平稳度确定窗口边界（使局部平稳度，同时满足窗口长度大于指定阈值），从而将原始信号划分成不等长的多个分段；之后，根据每个分段平稳度的大小，对窗口边界进行横向的延拓。对延拓后的信号求解包络线，再按原窗口大小对包络线进行裁切，从而保证在窗口边界处连续，且二阶导数连续，实现包络线的精确重构。LF-ASER（算法1）具体算法描述如下。

（2）调用AWS算法（adaptive window edge select algorithm），进行自适应窗口边界选择，得到各分段边界以及各边界点的局部平稳度。

（3）根据查找延拓代价表，确定该窗口的延拓代价。

（4）对窗口() 进行横向延拓，。

（6）重复执行步骤（3）～（5），计算各段包络线，对各分段进行连接，输出重构的整体包络线有()。

算法步骤（2）中AWS算法实现了自适应的窗口边界选择，在给定窗口长度最小阈值的前提下，对原始信号()，以第min个点为起点，逐点计算信号局部平稳度，确定窗口边界。()被划分为不定长的多个信号片段，每个片段的端点的值均小于1，AWS算法流程如图4所示。

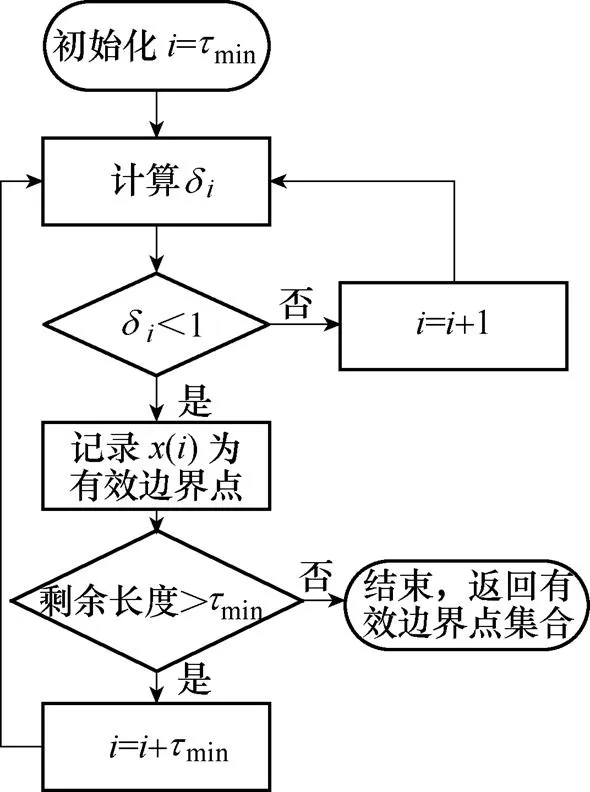
图4 AWS算法流程

在确定了窗口边界之后，各窗口边界的局部平稳度虽然均小于1，但大小不同，为获得相同的包络线误差，需要的延拓代价也不相同。为确定延拓代价，需要对分段包络线的误差进行定义。本文采用相对误差以衡量分段包络线的准确性，误差的定义为

2.4 并行化EEMD算法

算法1中对各分段求解包络线是采用循环方式串行完成的，计算量大、运行时间长。在分段进行延拓后，各分段数据相互独立，包络线的求解彼此没有依赖关系，因此适合采用MapReduce模型将算法并行化，以提高算法执行效率。

基于上述分析，提出并行化的EEMD算法（MR-EEMD）。在计算量大的信号包络线求解过程中对信号进行加窗分段，并行求解极值以及包络线。算法需要进行多次迭代计算，其整体流程如图5所示。

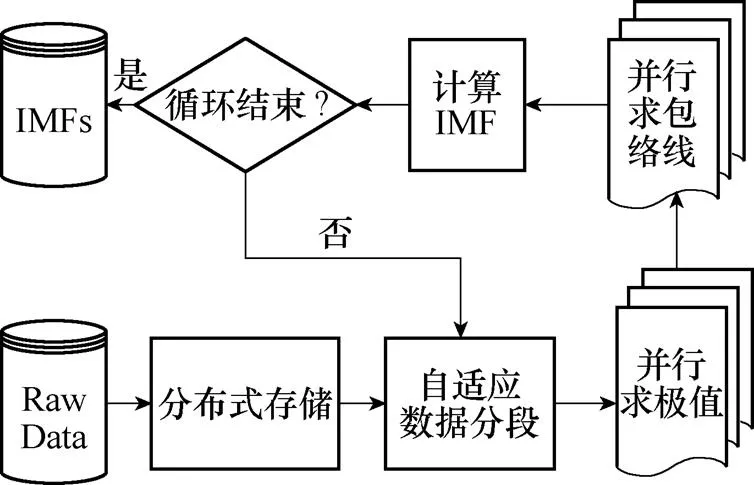
图5 MR-EEMD算法流程

MR-EEMD（算法2）算法计算过程描述如下：

（1）通过给原始信号()叠加一组高斯白噪声信号() 获得一个总体信号()。

（2）调用AWS算法，进行自适应的窗口边界选择。

（3）根据分段边界的信号局部平稳度，查找延拓代价表，确定该窗口的延拓代价。

图6 信号分段、延拓并转换为矩阵

（5）调用MR-Extremum算法，对波形记录矩阵中的各数据分段并行求取极值。MR-Extremum算法流程可简要描述为：在Map阶段，计算节点接收波形记录矩阵中的数据分段作为输入，并行地对分段中的记录逐点进行极值点判断，并记录极值点；在Reduce阶段，接收Map任务输出的局部极值片段并进行连接操作，输出极大值矩阵pmax，极小值矩阵pmin。

（6）调用MR-Envelope算法，对信号分段进行并行化的包络线求解。MR-Envelope算法接收MR-Extremum算法的输出（极大值矩阵pmax，极小值矩阵pmin）作为输入，在Map阶段，各数据节点的Mapper任务利用3次样条插值算法并行求解各分段的包络线，并根据之前的延拓代价对进行裁切（）；在Reduce阶段，Reducer任务对接收的包络分段进行连接重构，算法的输出为信号整体的上包络线和下包络线。MR-Envelope算法流程如图7所示。

图7 MR-Envelope算法流程

（7）求解包络均值，重复步骤（2）～步骤（6），得到各阶IMF分量。

重复上述步骤；利用高斯白噪声频谱的零均值原理，消除高斯白噪声作为时域分布参考结构带来的影响，原始信号对应的IMF分量为

3 实验

3.1 MR-EEMD算法去噪效果对比实验

为验证本文MR-EEMD算法去噪的有效性，选取某公司在线监测系统所采集局部放电实测数据进行分析。数据采样频率为5MHz，每个周期的信号是20ms，现场采集到的一个周期的局部放电波形，并将波形的局部放大，如图8所示。

图8 脉冲放大波形

从图中可以看出，采集到的信号噪声很严重，噪声的主要来源是周围的嘈杂环境以及周围设备带来的噪声。图9a为使用MR-EEMD去噪之后的信号波形，图9b为使用小波去噪后的信号波形。

图9 去噪后的脉冲放大波形

可以看到，小波去噪后的脉冲放大波形并没有很好地滤除噪声，还存在少量的周期脉冲干扰。而经过MR-EEMD方法去噪后，原信号中的背景噪声已经基本消除，较好地保留了其中的放电脉冲成分。

3.2 包络线相对误差限e、信号局部平稳度di与延拓代价di的关系实验

确定窗口边界后，各窗口边界的局部平稳度虽然均小于1，但大小不同，为获得相同的包络线误差，各窗口需要的延拓代价也不相同。在指定相对误差上限的前提下，需要一种快速有效的方法，根据窗口边界的局部平稳度确定该窗口的延拓代价。根据和从理论上倒推出最小的延拓代价的计算公式是困难的，本文采用实验的方式得出、与关系的经验数据，存储为表格，在算法执行时，通过查表快速获得窗口需要延拓的长度。

选取某公司在线监测系统所采集局部放电实测数据进行实验分析。从局部放电信号中，通过逐点计算局部平稳度，选取0＜＜1范围内的点作为窗口边界，对窗口进行延拓，求分段包络，并计算相对误差。延拓长度从1开始递增变化，记录每次产生的相对误差。将的变化范围等分为10个小区间，即，对每个区间，从实验样本中选取20个属于该区间范围的进行实验，通过递增，计算每次的包络线相对误差。图10绘制了0.2＜＜0.3时，4个（1=0.22，2=0.24，3=0.25，4=0.27，）的实验结果。从图10中可以看出，在确定后，相对误差随着延拓代价的增长而下降。平稳度相似时，形成的相对误差与延拓代价的曲线也相似。其他的实验结果曲线均具有上述性质。

图10 相对误差、信号平稳度与延拓代价的关系图

表1=1×10-3，与的关系数据

Tab.1 ɛ=1×10-3，relationship between δ and λ

表2=5×10-3，与的关系数据

Tab.2 =5×10-3，relationship between δ and λ

Tab.2 =5×10-3，relationship between δ and λ

d(0,0,1](0.1,0,2](0.2,0,3)(0.3,0,4)(0.4,0,5)(0.5,0,6](0.6,0,7](0.7,0,8](0.8,0,9](0.9,1) l2345566778

按照同样的方式，可以获得给定其他值时与的关系数据。在算法执行时，首先根据指定，确定待查询的表，然后根据所属的区间，确定需要进行延拓的长度。

另外，可根据需要，将所属区间划分为更细粒度，例如，每个区间的宽度取0.05，从而获得更准确的延拓代价。在数据的组织上，也可以将作为关系表的一列，从而将所有数据存储到1张表格内，表头设计可参考表3。

表3、与的关系表

Tab.3 ɛ, δ and λrelational table

3.3 并行化EEMD去噪性能分析

为验证所提并行算法运行时间性能，搭建了由19个节点组成的Hadoop云计算平台。每个节点的配置为4核CPU（Intel Core i5），主频2.60GHz，4GB RAM内存，1TB SATA7200rpm硬盘（64MB缓存），配备千兆以太网用于云平台节点的互联。每个节点的操作系统采用Ubuntu（Version 10.04 LTS），并安装Apache Hadoop（Version 0.20.2）云计算平台软件。将其中一个节点配置为主控节点（jobtracker，namenode），其他节点配置为计算节点（tasktracker，datanode），对每个计算节点，根据CPU核的数量配置map或reduce任务数量上限为4。HDFS块的大小配置为64MB，每个块配备3个物理备份，使用TestDFSIO[24]对集群的整体I/O性能进行了基准测试。

实验数据采用3.1节给出的变压器局部放电实测数据，采样频率为5MHz，每个周期的信号是20ms。在单机环境下（4核CPU，主频2.60GHz，4GB RAM内存），选取不同长度信号进行EEMD去噪，运行时间见表4。

表4 单机环境下EEMD去噪运行时间

Tab.4 Run-time of EEMD denoising in a single computer

可以看出，由于EEMD分解计算的复杂性，运行时间随信号长度呈非线性快速增长，对于长度为40 000点的信号，运行时间＞15min，工程实用性差。

在所搭建的云平台上运行MR-EEMD算法，选取不同长度的信号（500～100 000点）进行去噪处理，算法参数E（重复噪声次数）取100，std（噪信标准偏差比率）取0.2，窗口长度最小阈值min取5 000（信号长度小于5 000时，min取500），集群节点数19，运行时间如图11a所示。对图11a信号长度小于10 000的区域进行放大，得到图11b。

图11 EEMD与MR-EEMD运行时间对比

从图11中可以看出，EEMD去噪运行时间受信号长度影响很大，而MR-EEMD算法运行时间增长相对较平缓，在信号长度为40 000点时，运行时间仅为127s（单机运行时间大于15min），在信号长度为100 000点时，运行时间为565.1s，加速比达到7.2。由于集群通信开销等原因，在信号长度小于5 000时，EEMD运行速度更快，云平台优势不能体现。

为验证MR-EEMD算法的加速比，分别选取信号长度为50 000点（WL-1）和100 000点（WL-2）的两段样本进行实验。改变云平台规模运行MR-EEMD，云平台中计算节点数从2个至18个递增，统计程序运行时间，并计算加速比。MR-EEMD算法参数E取100，std取0.2，取5 000，加速比如图12所示。

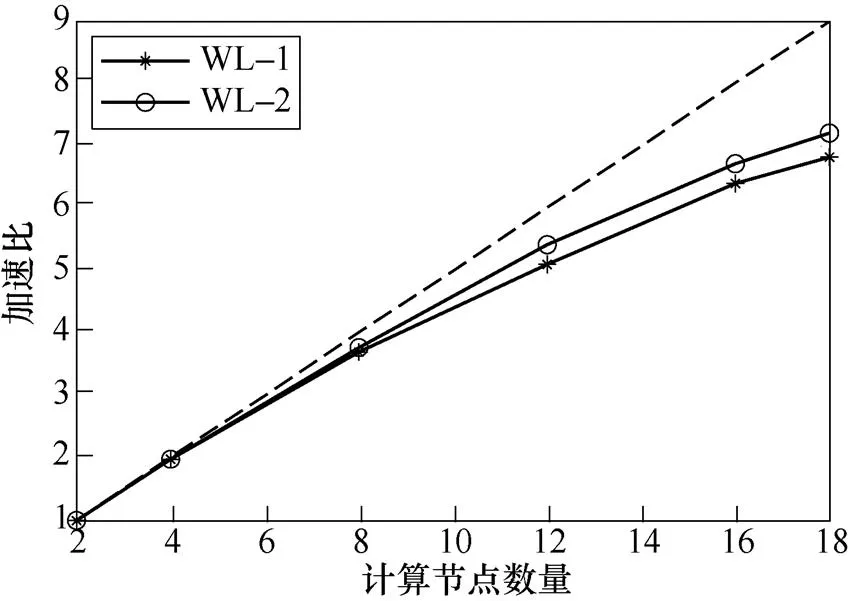
图12 MR-EEMD算法加速比

矩形窗口大小决定了MR-EEMD算法执行时并行处理的粒度，直接影响算法运行时间。对WL-1和WL-2数据样本，分别选取为1 000、2 000、5 000和10 000，运行MR-EEMD，统计运行时间，如图13所示。

图13 矩形窗口大小对运行时间的影响

从图13可以看出，WL-1在窗口长度为2 000时运行时间最短（相对本次实验的其他窗口长度），WL-2在窗口长度为5 000时运行时间最短。MR-EEMD运行时间受信号长度、窗口大小以及集群规模的影响，在集群规模一定的条件下，较小的窗口大小使得计算粒度更小，并行度更高，但节点间通信以及任务管理开销增大，需要进行折中选择，以达到最优运行效果。

除对变压器局部放电信号进行去噪处理，笔者课题组还将MR-EEMD用于某公司输电线路状态监测系统所采集的绝缘子泄漏电流信号、导线电流信号等数据处理，均保持了EEMD的处理效果，同时提高了计算效率。

4 结论

针对高采样率局部放电数据，提出了基于MapReduce模型的并行化EEMD算法MR-EEMD，并在云平台上进行了实现，使得在单机上运行缓慢甚至无法运行的程序变得可以运行。利用矩形窗口对信号进行分段时，考虑到矩形窗的固有缺陷，提出了基于局部平稳度的自适应分段包络线重构算法（LF-ASER）。该算法能够自适应地确定信号分段的边界和延拓长度，确保分段包络线在分段边界处连续，保持了原始EEMD算法特性。

利用实测数据，在Hadoop云平台上进行了去噪效果对比、MR-EEMD算法加速比、矩形窗大小对算法性能的影响等实验。实验结果表明所提方法能够有效处理高采样率信号，实现了快速的EEMD去噪，并取得了良好的去噪效果。下一步工作拟开展在内存计算平台上实现MR-EEMD算法的研究，以进一步提高算法的实时性。

[1] 郭俊, 吴广宁, 张血琴, 等. 局部放电检测技术的现状和发展[J]. 电工技术学报, 2005, 20(2):29-35. Guo Jun, Wu Guangning, Zhang Xueqin, et al. The actuality and perspective of partial discharge detection techniques[J]. Transactions of China Electrotechnical Society, 2005, 20(2): 29-35.

[2] 李化, 杨新春, 李剑, 等. 基于小波分解尺度系数能量最大原则的GIS局部放电超高频信号自适应小波去噪[J]. 电工技术学报, 2012, 27(5): 84-91. Li Hua, Yang Xinchun, Li Jian, et al. The maximum energy of wavelet decomposition approximation- related adaptive wavelet de-nosing for partial discharge UHF pulse in GIS[J]. Transactions of China Electro- technical Society, 2012, 27(5): 84-91.

[3] 江天炎, 李剑, 杜林, 等. 粒子群优化小波自适应阈值法用于局部放电去噪[J]. 电工技术学报, 2012, 27(5): 77-83. Jiang Tianyan, Li Jian, Du Lin, et al. De-nosing for partial discharge signals using PSO adaptive wavelet threshold estimation[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 77-83.

[4] Huang Norden E, Zhang Shen, Long Steven R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. The Royal Society, 1998, 454(1971): 903-995.

[5] 钱勇, 黄成军, 陈陈, 等. 基于经验模态分解的局部放电去噪方法[J]. 电力系统自动化, 2005, 29(12): 53-60. Qian Yong, Huang Chenjun, Chen Chen, et al. Denoising of partial discharge based on empirical mode decomposition[J]. Automation of Electric Power Systems, 2005, 29(12): 53-60.

[6] Lin Meiyan, Tai Chengchi, Tang Yawen, et al. Partial discharge signal extracting using the empirical mode decomposition with wavelet transform[C]. Inter- national Conference on Lightning, Chengdu, 2011: 420- 424.

[7] 李天云, 高磊, 聂永辉, 等. 基于经验模式分解处理局部放电数据的自适应直接阈值算法[J]. 中国电机工程学报, 2006, 26(15): 29-34. Li Tianyun, Gao Lei, Nie Yonghui, et al. A new adaptive direct-threshold algorithm to partial discharge data processing based on empirical mode decomposition[J]. Proceedings of the CSEE, 2006, 26(15): 29-34.

[8] Xu Jia, Yang Fan, Ma Fenghai. Research on nonstationary signal denoising based on EEMD filter[C]. International Conference on Multimedia Technology (ICMT), Ningbo, 2010: 1-3.

[9] 姚林朋, 郑文栋, 钱勇, 等. 基于集合经验模态分解的局部放电信号的窄带干扰抑制[J]. 电力系统保护与控制, 2011, 39(22): 133-139. Yao Linpeng, Zheng Wendong, Qian Yong, et al. A narrow-band interference suppression method based on EEMD for partial discharge[J]. Power System Protection and Control, 2011, 39(22): 133-139.

[10] 胡利萍, 宋恩亮, 李宝清, 等. 一种适用于流数据分析的快速EMD算法[J]. 振动与冲击, 2012, 31(8): 116-120. Hu Liping, Song Enliang, Li Baoqing, et al. A new fast EMD algorithm for streaming data analysis[J]. Journal of Vibration and Shock, 2012, 31(8): 116-120.

[11] Damerval C, Meignen S, Perrier V. A fast algorithm for bidimensional EMD[J]. IEEE Signal Processing Letters, 2005, 12(10): 701-704.

[12] Chen Q, Huang N, Riemenschneider S, et al. A b-spline approach for empirical mode decompositions[J]. Advances in Computational Mathematics, 2006, 24(1): 171-195.

[13] 胡劲松, 杨世锡. 基于有效数据的经验模态分解快速算法研究[J]. 振动、测试与诊断, 2006, 26(2): 119-121. Hu Jingsong, Yang Shixi. Study on valid-data-based EMD fast algorithm[J]. Journal of Vibration, Measurement & Diagnosis, 2006, 26(2): 119-121.

[14] Qin S R, Qin Y, Mao Y F. Fast implementation of orthogonal empirical mode decomposition and its application into singular signal detection[C]. IEEE International Conference on Signal Processing and Communications, Dubai United Arab Emirates, 2007: 1215-1218.

[15] White T. Hadoop: The Definitive Guide[M]. 1st ed. O’Reilly Media Inc, 2009.

[16] Dean J, Ghemawat S. MapReduce: Simplified data processingon large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113.

[17] 刘鹏. 云计算[M]. 2版. 北京: 电子工业出版社, 2011.

[18] Wu Z, Huang N E. Ensemble empirical mode decom-position: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[19] Wu T Y, Chung Y L. Misalignment diagnosis of rotating machinery through vibration analysis via the hybrid EEMD and EMD approach[J]. Smart Materials and Structures, 2009, 18(9): 7566-7579.

[20] Flandrin P, Rilling G, Gonçalvès P. EMD equivalent filter banks, from interpretation to applications[J]. Hilbert-Huang Transform and Its Applications, 2005: 57-74.

[21] George Tsolis, Thomas D Xenos. Signal Denoising using empirical mode decomposition and higher order statistics[J]. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2011, 4(2): 91-106.

[22] 唐炬, 许中荣, 孙才新, 等. 应用复小波变换抑制GIS局部放电信号中白噪声干扰的研究[J]. 中国电机工程学报, 2005, 25(16): 30-34.

Tang Ju, Xu Zhongrong, Sun Caixin, et al. Application of complex wavelet transform to suppress white-

noise interference in GIS PD signals[J]. Proceedings of the CSEE, 2005, 25(16): 30-34.

[23] 苗莎, 郑晓薇. 三次插值样条曲线拟合多核并行算法[J]. 计算机应用, 2010,30(12): 3194-3196. Miao Sha, Zheng Xiaowei. Multi-core parallel algorithm for cubic spline curve fitting[J]. Journal of Computer Applications, 2010, 30(12): 3194-3196.

[24] Michael G Noll. Benchmarking and Stress Testing an Hadoop Cluster With TeraSort, TestDFSIO & Co. [EB/OL]. 2011.4. http://www.michael-noll.com/blog/2011/04/09/benchmarking-and-stress-testing-an-hadoop-cluster-with-terasort-testdfsio-nnbench-mrbench/.

Research on Parallel Ensemble Empirical Mode Decomposition Denoising Method for Partial Discharge Signals Based on Cloud Platform

1,21,21,21,21

（1. North China Electric Power University Baoding 071003 China 2. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Beijing 102206 China）

Signal denoising is the primary issue when conducting online monitoring and diagnosing of electric transmission and transformation equipments. In view of the advantage of ensemble empirical mode decomposition (EEMD) for partial discharge signal denoising, the parallel EEMD algorithm based on Map Reduce model, named MR-EEMD, is designed to improve the computational efficiency by taking advantage of the cloud platform. In consideration of the inherent defects of the rectangular window, the local flatness-adaptive segmentation envelope reconstruction algorithm (LF-ASER) is proposed to compensate segmented boundary so that the envelope error can be reduced to a given threshold range. The experimental results show that MR-EEMD can be executed much faster than EEMD for the transformer partial discharge high sampling rate signal and maintains good denoising results, high scalability, and speedup.

Partial discharge, signal denoising, ensemble empirical mode decomposition, MapReduce, envelope reconstruction

TN911

宋亚奇 男，1979年生，讲师，博士研究生，研究方向为电力信息智能处理、云计算。

周国亮 男，1978年生，博士，副教授，研究方向为智能电网、大数据处理。

2013-08-24 改稿日期 2014-09-15

国家自然科学基金（61074078），中央高校基本科研业务费专项资金（13MS88、13XS30），新能源电力系统国家重点实验室和河北省自然科学基金（F2014502069）资助项目。